基于乘客路径选择的多制式轨道交通客流分配
倪少权,杨皓男,彭强
(1.西南交通大学,交通运输与物流学院,成都610031;2.综合交通运输智能化国家地方联合工程实验室,成都610031;3.综合交通大数据应用技术国家工程实验室,成都610031;4.中国铁路成都局集团有限公司,成都610031)
0 引言
轨道交通的客流分配是旅客运输计划制定的基础。寇俊等[1]将客流按照路径长短、旅途费用等因素分配到开行方案确定的运输径路上;蒲松等[2]利用计算机生成算法,将客流分配到不同径路中。为将列车间隔时间等运行图信息体现于客流分配中,佟璐等[3]在客流分配问题中加入车厢拥挤度对乘客的影响,但未考虑乘客对路网的熟悉度。周文梁等[4-5]分别建立旅客时段的弹性需求函数和换乘网络对客流进行分配。既有研究仅考虑单制式轨道交通的客流分配,然而在客流分配中需考虑不同制式轨道交通间的协同性,建立多制式轨道交通网络模型。
随着轨道交通网络发展,对多制式轨道交通协同的研究日益增多,高鹏等[6]利用灰色关联度模型对重庆市多制式轨道交通换乘时间的可靠性进行研究。王昊等[7]运用熵值赋权法对多制式区域轨道交通的协同主次进行研究,但未讨论乘客在不同出行路径中轨道交通的主次。
既有研究针对不同旅客采用固定线网熟悉度值,未考虑旅客在多制式轨道交通网络中,随起讫点及途径交通网络复杂程度差异而导致的线网熟悉度值差异,部分轨道交通可预先购票,旅客常在购置车票时制定出行计划,出行计划的制定时间是否充裕亦会导致熟悉度差异,多制式轨道交通出行除考虑单制式换乘影响,还考虑不同轨道交通线网间衔接关系对乘客出行路径的影响。本文构建消除隐性连接的多制式轨道交通构建多层复合网络,从时间衔接性,换乘节点衔接性出发得到线网间衔接性系数,基于线网复杂度函数及乘客购票时期强度函数确定可变线网熟悉度值,建立基于乘客路径选择的多制式轨道交通客流分配算法,解决不同制式轨道交通间客流数据分离,联系不紧密的问题。
1 多制式轨道交通网络拓扑网络构建
多制式轨道交通间各成体系,实际交通网络中存在大量隐性连接,在多制式轨道交通复合网络中显性连接与隐性连接可能同时存在,不同制式轨道交通间不能直接同站换乘,需经步行或骑行换乘的情况在拓扑图中表现为隐性连接。
事实上,乘客进行不同制式轨道交通换乘时,即便不能同站换乘,乘客亦会考虑距离较近的车站进行换乘。在多层多制式轨道交通拓扑网络中,距离较近的不同制式车站在层间并无连接边,表现为隐性连接,乘客无法选择此路径,需消除隐形连接以正确得到乘客对不同出行路径的选择概率,同时引入虚拟换乘站使换乘关系能直接在邻接矩阵中得到体现。
1.1 消除网络隐形连接
将相距较近的地铁车站与其他轨道交通车站在拓扑网络层间建立显性连接,即连接边。处理方法如下:设高铁、城际列车车站数共有n个,其组成集合N分别对这n个车站周边的地铁车站进行处理。设s是和地铁车站i相邻的高铁或城际列车车站,s∈[1,n] ,n∈N。Lis代表i,s间的距离,tis代表i,s间的换乘走行时间。若地铁车站i与高铁、城际列车车站s的直线距离Lis小于车站最小独立间距Lis,min且换乘时间tis小于车站最小独立换乘时间tis,min,则在两车站间建立连接关系,同时构建消除隐形连接后两车站的邻接矩阵M′,经问卷调查,旅客认为两站间Lis和tis分别小于1 km 和10 min时换乘方便,会近似将两车站视作不同制式轨道交通换乘站,故Lis,min,tis,min分别取1 km,10 min。
1.2 单层网络中换乘点处理
图1为虚拟换乘站引入示意图。将线路a-换乘站-线路b的换乘模式转化为线路a-虚拟换乘站1-虚拟换乘站2-线路b的换乘模式。
1.3 拓扑网络构建
拓扑网络拟采用SPACEL方法进行处理,以上述网络处理原则构建城市轨道交通网A、城际列车铁路网B、铁路网C的三层拓扑网络。分别构建单层网络邻接矩阵MA,MB,MC,层间换乘邻接矩阵MAB,MAC,MBC,层间消除隐性连接的站间邻接矩阵,层间换乘站集合LAB,LAC,LBC,层间消除隐性连接的车站集合L′AB,L′AC,建立拓扑网络示意图如图2所示。图中,实心点为不同制式轨道交通层间实际换乘站,空心点为消除隐性连接的车站。
1.4 多制式轨道交通线网衔接性
多制式轨道交通线网间的衔接性在一定程度上影响旅客出行路径选择,乘客倾向选择线网间衔接性较好的路径出行,不同轨道交通线网间衔接性分为时间衔接性和换乘节点衔接性。
(1)时间衔接性
以A,B交通方式为例,令A一天的开行频次为NZ,A,途径LAB,L′AB的班次中在B运营服务时间外的班次数量为NC,AB,同理得到NZ,B、NC,BA,则A,B时间衔接性τt,AB为

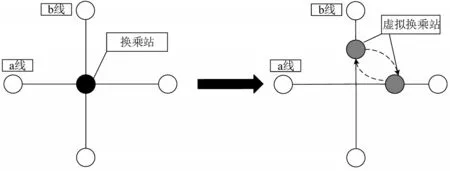
图1 虚拟站添加示意图Fig.1 Schematic diagram of adding virtual station
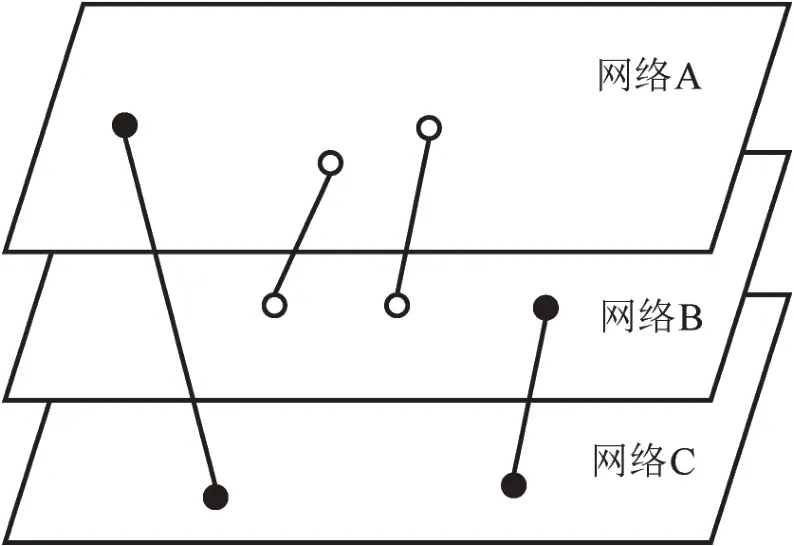
图2 拓扑网络示意图Fig.2 Topological network diagram
(2)换乘节点衔接性
引入换乘站线网辐射度概念,A,B线网中LAB,L′AB不进行同制式换乘能到达的车站数量NF,AB与A,B线网内车站总量NA+NB的比值,称之为A,B线网换乘站线网辐射度。辐射度τp,AB为

式中:τp,AB∈(0,1] 。
换乘站线网辐射度越高则换乘站衔接性越好。不同制式线网间衔接性系数τAB为

式中:μ为衔接性校正系数。基于历史数据,运用专家评估法进行参数确定,本文μ取0.3。
2 有效路径确定及最短路搜索算法
多制式轨道交通网络中不是所有路径乘客都会考虑,如迂回过多的路径等,为减少多余路径提高最短路搜索效率,给出有效路径的确定方式,Rk(rs)为rs弧的第k条路径,Ck(rs)为Rk(rs)路径的广义出行费用,通过设立绝对阈值与相对阈值的方式对路径出行费用加以限制。设绝对阈值为,放大系数为fmax,广义出行费用应小于绝对阈值与经放大后的放大阈值两者的最小值。

除对广义费用进行限制外,还应对换乘次数与换乘交通方式加以限制。设Nk(rs)为Rk(rs)弧上的换乘次数,为弧上不同交通方式换乘次数。、都应小于各自的换乘次数阈值Nmax、Nm,max。
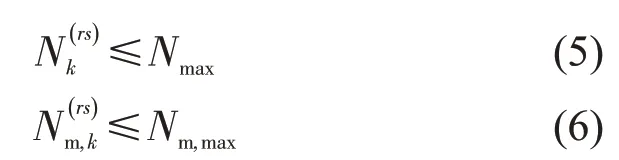
根据文献[9]设置fmax为15%,为20 min,Nmax为4 次,因网络共有3 种轨道交通方式,故将Nm,max设置为3次。
单层中最小费用路径搜索算法采用Dijkstra算法实现。若起讫点分处不同层间,则分别计算起点层中起点至不同交通方式换乘点的K 短路径及终点层换乘点至终点的K短路径,将换乘点相同的不同层K短路径两两求和相加,比选出最优路径。图3为路径搜索示意图。
3 基于乘客出行路径选择的客流分配模型建立
3.1 路径选择概率模型确定
采用Logit模型进行客流分配,根据MML模型可得区域多制式轨道网络中起讫点为r,s路径的第k条路线的选择概率为

式中:θ为乘客对线网熟悉程度值;ck(rs)为不同路径的效用值,建立基于线网复杂度和乘客主观线网了解行为的线网熟悉程度,并根据乘客路径选择影响因素确定路径效用值,计算各路径的选择概率。

图3 路径搜索示意图Fig.3 Path search diagram
3.1.1 乘客线网熟悉度确定
传统客流分配中,预测者常把MML 模型中乘客对线网熟悉程度值设为定值,线网越简单则熟悉程度值越高。多制式轨道交通线网复杂且不同乘客路径上的网络情况不同,致使每位乘客对网络的熟悉程度偏差较大,制定出行计划的时间不同,熟悉程度同样也会发生改变。借助网络复杂度及客票购买高峰时期给出不同路径中乘客的网络熟悉程度。
(1)多制式轨道交通网络复杂度对网络熟悉度的影响
多制式轨道交通网络复杂度的影响因素主要为换乘节点数量与网络中线路数量。起讫点rs中第k条路径乘客所感受到的线网复杂度为

式中:p为路径所经过的所有轨道交通线网集合;np为单层线网的换乘节点数量;hp为单层线网中的线路数量;nc为线网间换乘节点数量。乘客所经过的线网复杂度越高则乘客对线网熟悉度越低。
(2)出行计划制定时间对网络熟悉度的影响
本文三层多制式轨道交通模型中,高速铁路和城际列车两种交通方式会提前放票。乘客购买车票距离发车时间越早,往往拥有越长时间了解线网,网络熟悉度也随之提高。利用文献[8]客票购买强度函数,可求得多制式轨道交通网络中不同线路的售票强度高峰时间区段,旅客购票强度函数为
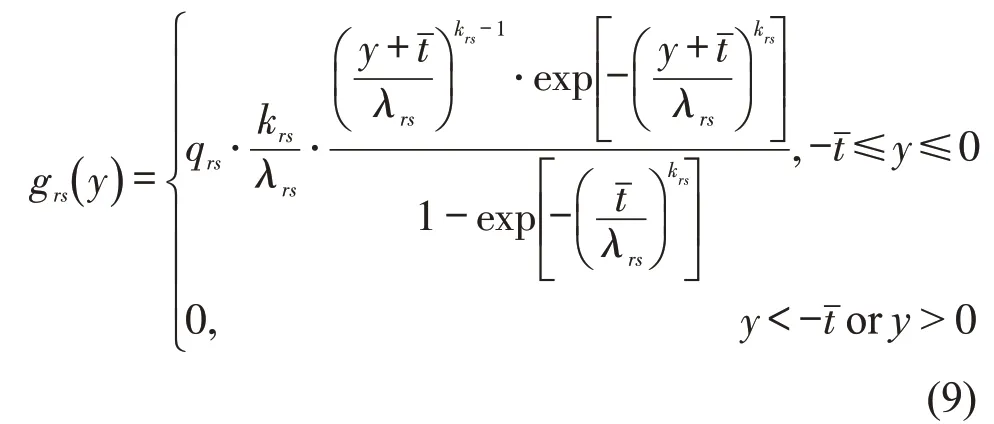
参数λrs和krs表达式为
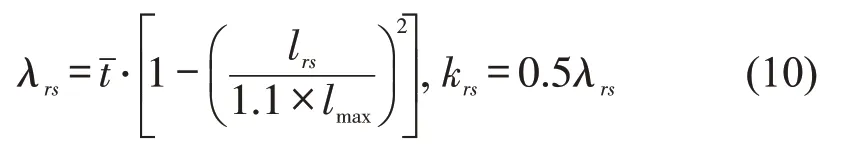
式中:y为旅客购票时间;λrs和krs为与线网指标相关的放大系数;lrs为OD对(r,s)在线网上的最短路径rs;lmax为线网中的最长路径;ˉt为客票放出点与客车始发时间的差值;grs(y)与累计总量qrs的比值即为购票强度。
起讫点r,s中第k条路径的出行计划制定时间为

式中:N为所有提前放票的轨道交通线路集合,n∈N;yn为第n类轨道交通客票购买强度最大时的y值。旅客常在初次购票时即开始制定出行计划,值越大则出行计划制定时间越早,乘客对线网熟悉程度越高。
(3)线网熟悉程度值确定
文献中常将线网熟悉度θ控制在[0.05,5.00]。本文将θ在基础值上根据影响因素进行调整。

式中:f1、f2分别为网络复杂度及出行计划指定时间对线网熟悉程度的影响因素;θ为熟悉度基础值,文献[9]中利用数据资料和问卷调研结果拟合得到常规交通线网熟悉度值为2,本文θ取2。
3.1.2 广义出行费用函数
基于乘客路径选择的影响因素建立广义出行费用函数,广义出行费用由基本费用、惩罚费用、不同制式轨道交通线网换乘衔接性系数构成,用以确定各路径效用值。
(1)基本费用
①乘车时间
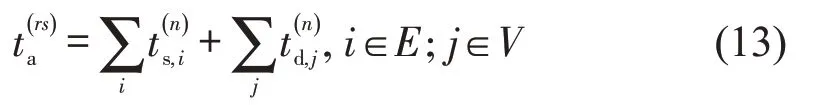
式中:为第n层网络列车i区段运行时分;为n层网络列车在j站的停站时间。
②候车时间

式中:为不同制式轨道交通换乘接续列车n发车间隔时间;δ为不同制式轨道交通组合方式集合,为同制式轨道交通换乘列车n的发车间隔时间;γ为轨道交通方式集合;x为0-1变量。
(2)惩罚费用
①换乘费用
不同制式轨道交通的换乘为

②票价费用影响
不同制式间的换乘势必会带来出行价格上的差异。

式中:为不同制式车辆在起讫点r,s中各自运行区段的运行费用之和;eϕ为一种轨道交通在其线网上的运行费用;ϕ为不同轨道交通在其线路上运行的区段。
由于其他影响费用单位皆为时间,利用国民年均生产总值转化票价费用影响得到(min)为

综合考虑基本费用、惩罚费用得到广义出行费用为

式中:为对弧rs中第k条有效路径的费用估计值;λ为各制式列车的拥挤度系数;τk为路径k途径线网间衔接性均值;σ为修正系数,费用单位为min。
3.2 参数拟合及算法流程
运用多元回归参数估计方法对模型利用SPSS软件进行参数拟合,通过问卷调查及参考现有研究成果得到拟合参数如表1所示。

表1 拟合参数汇总Table 1 Summary of fitting parameters
具体客流分配算法流程如下:
Step 1 输入各线网基础OD 客流数据,得到起讫点为r,s的路径客流量,记为qrs。
Step 2 记录每条OD 路径途径的线网类别,计算路径途径线网间衔接性均值τk,并计算路径总复杂度ϖk(rs)。将路径中具有可提前购票区段的路径置入Eadv,转入Step 3;无可购票区段的路径置入Enom,代入式(12)计算出乘客对出行途径线网的熟悉程度θ′。
Step 3 计算路径的出行计划制定时间,结合计算乘客对出行途径线网的熟悉程度θ′。
Step 4 利用Dijkstra路径搜索法在三层网络模型上搜索起讫点为r,s的K短路径,计算r,s间各条路径的广义出行费用和最小出行费用,确定r,s间的有效路径集Rk(rs)。
Step 5 根据Logit 模型计算r,s间各条路径的选择概率pk(rs)。
Step 6 计算每条路径上的客流量fk(rs),计算公式为
Step 7 以路径客流量fk(rs),计算r,s区间i流量x1(rs),计算公式为。根据r,s区间第k条路径是否包含区间a,分别令为1和0。
Step 8 重复Step 6和Step 7,计算全网所有OD对的路径客流量和区间客流量,得到区间i的断面客流量
4 实例验证
以成都地铁、成灌及成贵城际列车开行段、成渝及西成高铁线路为例分析模型与算法的有效性。截至2019年12月,成都地铁共开通7条线路,共计207座车站投入运营(换乘站不重复计算),其中,18座换乘站,与城际列车线路和高铁线路换乘站共3 个。构建地铁网、高速铁路网、城际列车网三层复合网络模型,部分层间换乘信息如表2所示。
表3为2019年4月9日成都地铁部分OD客流。表4为高铁线路、城际列车部分OD客流。

表2 城际列车线网与地铁线网换乘信息Table 2 Intercity train line network and subway line network transfer information

表3 成都地铁部分OD客流Table 3 Part of OD passenger flow of Chengdu Metro

表4 高铁线路、城际列车部分OD客流Table 4 Part OD of high-speed rail lines and intercity trains
使用matlab 求得部分OD 对的有效路径、效用值及选择概率等信息,如表5所示。分析都江堰-华西坝的3 条有效路径,如图4所示。
3 条路径长度相近,效用值及选择概率却有较大差异。路径2换乘次数较多,其效用值明显高于路径1;路径3换乘次数虽最少,但需在成灌快铁线路上乘坐较远距离,在所有路径中拥有最高的出行费用,同时路径1、2的多制式轨道交通换乘车站犀浦站已实现同站换乘,路径3的不同制式轨道交通换乘需站外换乘,换乘时间费用较大。调研100名群众在都江堰至华西坝的路径选择,选择路径1、2、3的概率分别为85%,11%,4%,与预测概率结果相近,证明了Logit模型的有效性,此模型可为旅客多制式轨道交通出行提供路径选择建议。
基于乘客路径选择的多制式轨道交通客流分配算法得到成都地铁线网和成灌线路的部分区段日均断面客流量,因篇幅原因,仅展示成都地铁线网及成灌线客流分配图,如图5和图6所示。
由图5可知,地铁线网客流主要分布在七号环线内部的1、2、3号线位区段,部分区段客流已超过满载率,运营部门可调整客流较大区段的列车开行频次。图5和图6中轨道交通线网与其他轨道交通方式的换乘车站如火车南站、火车北站等附近客流量较大,衔接区段的分时客流可为不同交通方式间的接续方案制定提供数据支撑。
将本文分配得到的部分区段日均断面客流与查阅所得的断面客流进行对比印证,结果如表6所示。
与实际OD 客流数据比较,代入可变与固定的乘客熟悉度的分配结果平均误差率分别为13.25%、9.61%,可知,代入可变乘客熟悉度的客流分配算法更优,验证了客流分配算法的准确性和有效性。多制式轨道交通线网客流分布情况对运营部门制定不同制式间相互衔接的旅客运输计划提供支撑。

表5 部分OD路径选择概率及相关信息Table 5 Partial OD path selection probability and related information

图4 具体有效路径Fig.4 Specific effective path

图5 地铁客流分配图Fig.5 Metro passenger flow distribution map
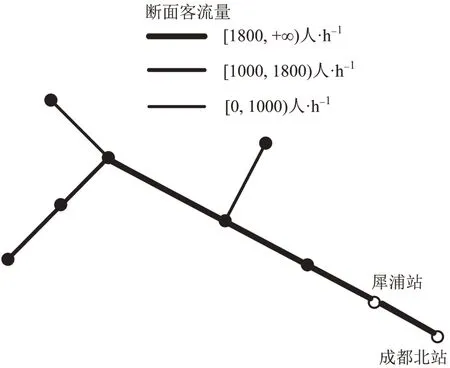
图6 成灌线上客流分配图Fig.6 Passenger flow distribution on Chengguan line map
5 结论
本文针对乘客出行特点,研究多制式轨道交通的客流分配,加入虚拟换乘站量化换乘对乘客出行路径选择的影响程度,基于可变的线网熟悉度函数与乘客影响因素,建立客流分配算法,实现多制式轨道交通的客流分配。

表6 对比结果展示Table 6 Comparison result display
实例验证表明,客流分配结果与实际值误差较小,在线网上的客流分配结果具有真实有效性。计算乘客路径选择概率时,代入可变的乘客路网熟悉程度值,其结果优于固定不变的线网熟悉程度值,该分配算法能有效得到多制式轨道交通线网中的客流分配情况,并能较好地反映线网中运输能力饱和区段,具有一定实用价值。

