城市交叉口交通控制模型的退化研究

张立立，赵琦，王力，刘建东，张玲玉，李凯龙

(1.北京石油化工学院，信息工程学院，北京102617；2.北方工业大学，城市交通智能控制技术北京市重点实验室，北京100144；3.中国公路工程咨询集团有限公司，北京100191)

0 引言

以传统城市道路交通控制理论为基础，结合现代控制、智能控制、人工智能等理论的模型与算法在交通控制领域得到长足的发展和应用，并形成许多细分研究领域和分支。现代控制理论假设受控对象的数学模型已知，基于现代控制理论的交通控制方法大多称为基于模型的交通控制理论与方法[1-2]。交通信息化的推进和检测技术的发展使得交通检测数据的种类、精度得到极大提升，同时，道路交通出行需求的爆发式增长使得传统交通控制方法无法满足需要，研究人员开始思考基于数据驱动的交通控制理论与方法[3-4]，即考虑在难以对受控系统准确建模时，仅利用系统的输入、输出数据实现控制与决策。近年来，人工智能理论与方法的突破和大规模云计算与边缘计算技术的演进，推动了以人工智能方法为核心的新型智能控制的发展，部分学者提出了基于人工智能的交通控制理论与方法[5-6]。

先进技术的进步推动了交叉口交通控制理论与方法的发展，在增加控制变量丰富性的同时，也使交通控制模型愈发复杂。导致的问题是先进交通控制模型在理论研究中效果明显，在实际应用时经常发生模型失配，即实际中的约束条件往往导致某些控制变量或相应的控制策略无法执行，出现交通控制模型退化(模型泛化能力降低)的现象。本文从该现象入手，分析导致模型退化的原因并研究退化的形式。

1 问题描述

为研究交通控制模型的退化现象，需要构建多变量交叉口交通控制模型，该模型包含：车速、车道、相位、相序和绿灯时间5类控制变量，通过控制变量实现路段速度、车道、交叉口相位、相序和绿灯时间控制。将交叉口间连接路段分为控速区和控道区。控速区表示连接路段上车辆可以自由换道区域，实施速度控制减小车流的离散特性，实现车流达到均匀性；控道区表示交叉口进口道车辆需按照车道类型通行的区域，实施车道控制增加车流流向的分割，实现车流通行需求的主动调控，如图1(a)所示。

由图1(b)、(c)建立具有多控制变量交叉口交通控制模型的存储转发形式为

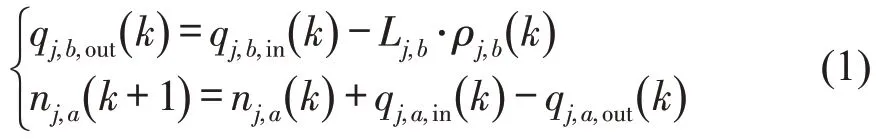
式中：nj,a(k)为路段j,a在采样周期k的车辆数；qj,a,in(k)为采样周期k内上游路段发送给路段j,a的流量；qj,a,out(k)为采样周期k内路段j,a发送给下游路段的车辆数；qj,b,in(k)为k时段内路段j,b的输入流量；qj,b,out(k)为k时段内路段j,b的输出流量；ρj,b(k)为k时段内路段j,b的交通流密度；Lj,b为路段j,b的长度。

式(1)表示采样周期k+1 内路段j,a的车辆数，等于采样周期k内路段j,a上的车辆数与上游路段流向j,a的车辆数和流出j,a的车辆数差的和；路段j,b流出的车辆数等于流入车辆数与存在车辆数之差。

令qj,b,out(k)=qj,a,in(k)，则式(1)变为

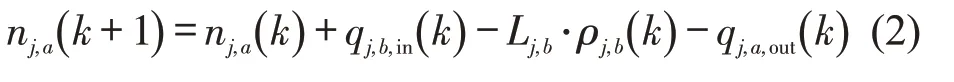
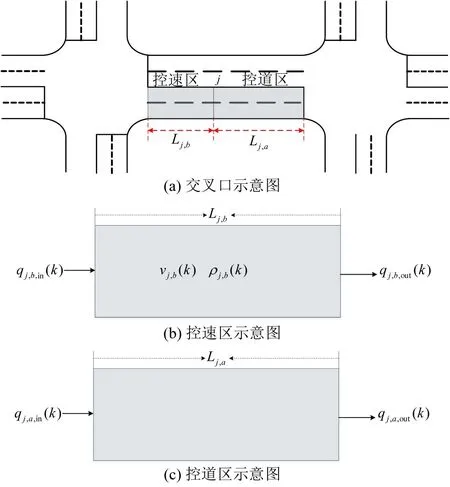
图1 交叉口交通控制模型Fig.1 Active traffic control model at intersection

根据文献[9]，得到交叉口交通控制模型为

式中：V(k)为速度控制模型，提供车速控制变量；G(k)为车道控制模型，提供车道、相位、相序和绿灯时间4 个控制变量；ϖj,a,o(k)为车道控制变量；为相位控制变量，X和x表示上下游路段连接与相位数量；Sj,a为路段通行能力；gj,a,o(k)为采样周期k内路段j,a所在相位的绿灯时间，gj,a,o,min为采样周期k内路段j,a所在相位的最小绿灯时间，且有gj,a,o(k)≥gj,a,o,min。

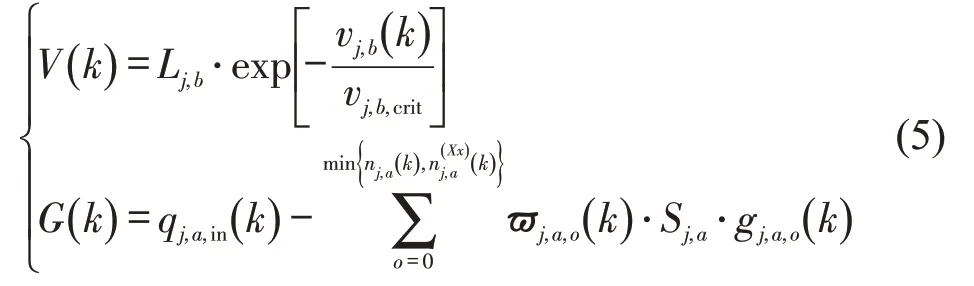
式中：vj,b(k)为速度控制变量；vj,b,crit为临界速度；vcrit为临界车速；ρjam为拥挤密度。

2 交通控制模型退化分析

2.1 模型退化的原因

导致交叉口交通控制模型退化的原因主要有以下3种：

(1)控速区路段长度达不到速度控制要求，即Lj,b ＜Lj,b,min，其中，Lj,b,min表示控速区最小长度。

(2)执行器不能执行。执行器分为两类，一类是车速控制执行器，一类是车道及信号控制执行器。

(3)驾驶者在控速区对限速的遵从率不足。

当上述情况发生时，以式(3)为完整形式的交叉口交通控制模型出现退化。退化过程如图2所示，其中，ϑ1,ϑ2,…,ϑn为退化因子。

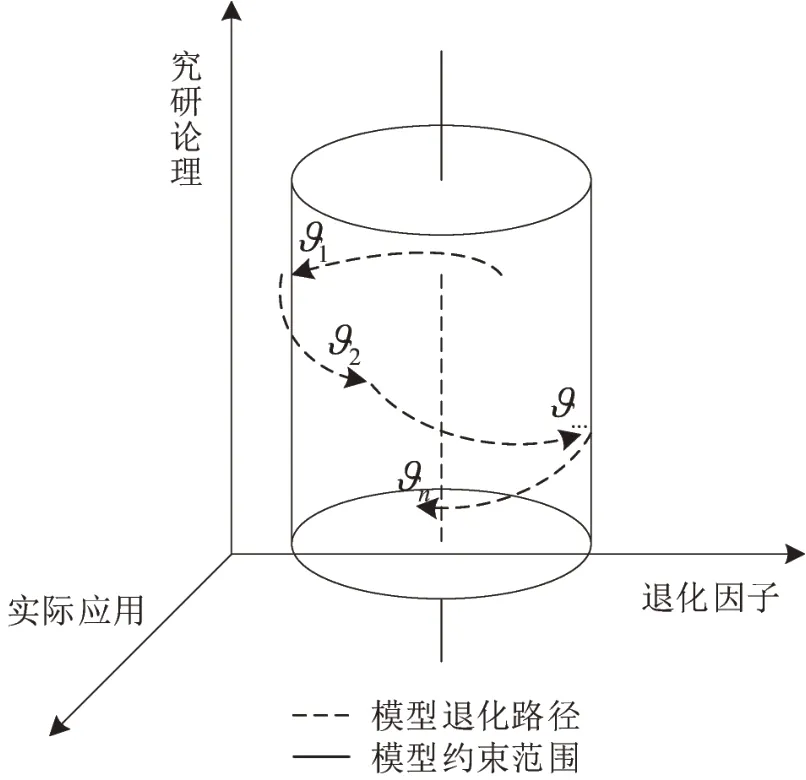
图2 模型退化过程Fig.2 Degenerated processes of model

2.2 模型退化的形式

(1)模型退化因子

假设ϑ={θr,θc,a,θc,b,θf}，为退化因子集合，具体描述如表1所示.

(2)模型退化过程

交叉口交通控制模型为

①当退化因子ϑ表现为：θi,r=0 或θi,f =0 或θi,c,a=0 时，存在V(k)=0，则式(6)退化为

其中，

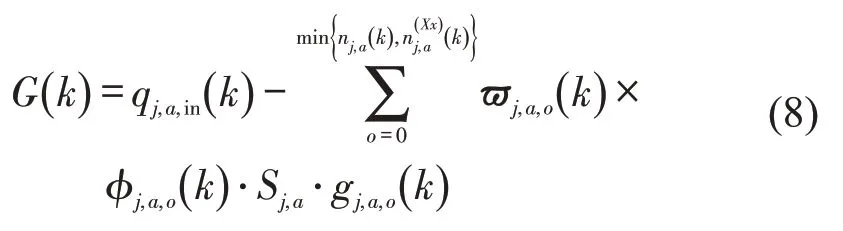
式(7)表示控速区消失，无法实施速度控制，可以实施车道、交叉口相位、相序和绿灯时间控制，其中，φj,a,o(k)表示车道属性变量。

②当退化因子ϑ表现为：θi,r=0 或θi,f =0，且θi,c,a=0 时，存在vj(1)(k)=0 和ϖj,a,o(k)=h，φj,a,o(k)=H，h和H为常值，则式(6)退化为

其中，

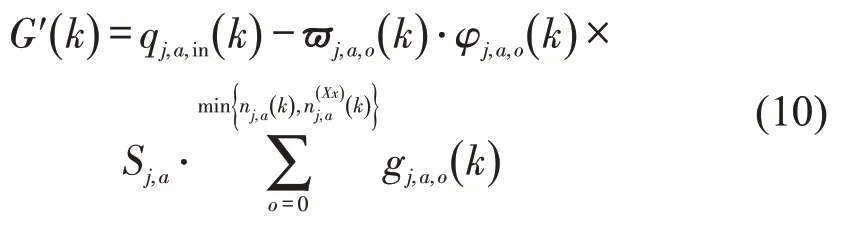
式(9)表示控速区消失且车道方向属性无法表达，无法实施速度控制和车道控制，可以实施交叉口相位、相序和绿灯时间控制。

表1 模型退化因子描述Table 1 Description of model degradation factor

③当退化因子ϑ表现为：θi,r=0 或θi,f =0，且θi,c,a=-1 时，存在vj(1)(k)=0 和ϖj,a,o(k)=h，φj,a,o(k)=H，h和H为常值，并且o=1,2,3，则式(6)退化为

其中，

式(11)表示控速区消失，车道方向属性无法表达和相序不能调整，无法实施速度、车道、交叉口相位和相序控制，可以实施绿灯时间控制。

交通控制模型从式(6)退化到式(7)时，控制变量：车速、车道、相位、相序、绿灯时间的解空间将逐渐缩小，直至退化到式(11)。

3 仿真分析

3.1 实验参数设置

为对模型退化各阶段控制策略的控制效果进行对比分析，在OSP 仿真系统中选取欠饱和、过饱和两个场景进行实验。以交叉口F 为控制策略实施对象，仿真路网如图3所示，图中字母表示路口编号。仿真参数如表2所示。

图3 仿真路网Fig.3 Simulation of road network

表2 仿真参数设置Table 2 Simulation setting

3.2 模型退化结果对比分析

图4为不同控制策略对交叉口通行能力系数变化的影响，其中，FC 为定时控制策略[7]；SC 为交叉口切换控制策略[8]，DC 为动态车道控制策略[9]，AC为主动交通控制策略[9]。通行能力系数JS为

式中：Δdj,a(k)为采样周期k内路段j,a的排队长度的差；dˉj,a为单车平均长度；dj,a(k)为采样周期k内路段j,a的排队长度。

图4 通行能力系数变化Fig.4 Change of capacity coefficient

由图4可知，采用SC、DC 和AC 这3 种控制策略的控制效果均好于定时控制策略，并且在JS＞0时，DC 和AC 的控制效果相同，原因是在该条件下两者采用的方法相同(均为动态相位控制)；当JS＜0 时，DC 与AC 的控制效果交替，当AC 启动车道控制时，效果明显好于DC，这是由于在该条件下DC 多次实施车道控制，使JS在阈值附近波动，但其所具有的滞后性无法及时适应交通流的快速变化；同时，当场景由过饱和转向欠饱和时，SC 的控制效果与AC 相近，原因是其为适应交通流变化的速度更快。

图5为模型退化不同阶段的控制效果对比，可知，与FC、SC、DC 这3 种策略相比，AC 控制策略能够有效降低交叉口平均停车延误时间和平均停车次数，DC 相比于SC 和FC 有较高提升。由此可知，在模型退化过程中控制策略对交叉口的控制效果逐步降低，充分说明交叉口的交通控制模型在理论研究和仿真中效果明显，而在实际应用时经常因控制变量不能被执行而出现模型失配，进而降低控制效果。

图5 模型退化不同阶段的控制效果对比Fig.5 Contrast of control effect in different stages of model degradation

由此，模型退化现象的存在性得以证明，同时也表明，本文所提模型退化概念的有效性。根据模型退化产生的3个本质原因，为预防模型退化现象的发生，在交通控制模型的实际应用中应考虑如下措施：

(1)根据实际道路和交叉口条件选择匹配的控制模型。

(2)所选用的交通控制模型需要有完善的数据感知条件支撑。

(3)如果所用模型具有速度控制能力，需要考虑控速区路段的长度以保证速度控制的实施。

(4)如果所用模型为主动控制模型，对于新建道路和交叉口应该充分安装速度控制器(如动态限速控制板)，车道及信号控制器；对于非新建道路和交叉口应该根据存在的设备情况考虑选择适合的模型实施控制，同时要保障设备的正常运行。

(5)采用违章抓拍、信息提示等手段促使驾驶者遵从速度控制、车道控制等要求，以提升控制遵从率，保障控制策略实施的有效性。

未来在车路协同、自动驾驶环境下，交通控制模型将发生本质变化，预防模型退化的方式也将发生相应变化。

4 结论

本文立足交通控制模型失配问题，提出交通控制模型退化概念并详细分析导致模型退化的3 个本质原因，得到模型退化的基本形式和演化路径。利用仿真对所建交通控制模型在定时控制、切换控制、动态车道控制和主动控制策略下的退化控制结果进行对比分析，结果表明，随着模型退化的加剧，交叉口的控制效果逐步降低。本文研究结果和建议能够有效避免交通控制模型在实际应用发生模型退化的情况。模型退化问题的产生对交通控制的实际应用有很大影响，未来需要进一步深入研究模型退化机理、退化预防和控制策略适配等问题。