基于自然驾驶跟车数据的驾驶人差异性分析与辨识

刘志强，张凯铎，倪捷

(江苏大学，汽车与交通工程学院，江苏镇江212013)

0 引言

为尽可能地降低因驾驶人因素导致交通事故的发生率，减轻驾驶人操作强度，先进驾驶辅助系统(ADAS)在近几年发展迅猛。然而，驾驶人因个体属性、心理特征、对信息的决策处理能力不同，在跟车、换道、制动等方面表现出典型的差异性，现有ADAS 系统鲜有根据驾驶人真实驾驶习性采取不同控制策略，导致驾驶人对ADAS系统的接受度和使用率均较低。为满足ADAS个性化用户需求，提高驾驶人对ADAS的信任度与接受度，更具先进性的驾驶辅助应能针对不同驾驶人个体或群体，进行驾驶人行为特性的自适应调控。

自适应于驾驶人特征的辅助驾驶技术离不开对驾驶行为的深刻理解，近年来基于自然驾驶数据的驾驶行为研究成为热点。学者提取不同行车参数特征实现对驾驶行为差异性的分析与辨识，常用的指标包括车速、加速度、方向盘转角、制动踏板力等。Yi等[1]基于自然驾驶实验数据，利用高维特征可视化方法，比较分析速度、转向角等参数，建立个体差异性辨识指标，并对5 位驾驶人进行识别，其准确率达91.6%。Fung 等[2]以加速度次数、急加减速次数等中微观特征对5位老年驾驶人进行区分，提取均值、最值等统计特征作为输入，准确率约为61%。Luo[3]等使用车辆传感器收集的多变量时序信号，提出一种区间特征划分方法提取关键特征，对4位驾驶人进行识别，准确率达89%。Bernhard[4]等基于横向车辆运控数据，提取驾驶人转向角参数，做对数傅里叶变换处理，对15 名驾驶人识别时，准确率达到76%。在差异性辨识中，多种机器学习方法，如支持向量机(SVM)[5]、人工神经网络(ANN)[6]、随机森林(RF)[7-8]等表现出较好的识别效果。机器学习方法往往需要利用相关领域知识进行特征构建，上述方法大多以驾驶人之间存在差异为前提，使用不同行车参数的统计特征作为特征输入，少有对数据之间的差异性进行时域和频域的深入分析，关键特征有待进一步发掘。

基于此，本文通过实车实验，开展跟车工况下的驾驶行为差异性研究，通过统计分析、频域分析和时频分析，开展驾驶人跟车行为参数的多尺度细化，进行个体驾驶行为的特征提取，并建立基于随机森林的驾驶人辨识模型。为实现驾驶行为的精准化描述，推动辅助驾驶系统的发展提供依据。

1 数据采集与预处理

1.1 实验过程

实验招募8名驾驶人，年龄为26～46岁，平均年龄为37.5岁，标准差为6.6岁；驾龄为2～26年，平均驾龄为10.3年，标准差为8.4年，年平均驾驶里程为1.0 万～2.5 万km。在实验前告知被试注意事项，让其按照日常驾驶习惯自由驾驶，实验过程中被试不佩戴任何仪器，不对被试做任何干扰，确保数据真实可靠。实验路段选取镇江市金港大道快速路基本路段，全长29 km。道路为双向8车道，以中央隔离带分隔，限速值为100 km·h-1。实验时间避开高峰时段，安排在上午9:00-10:30 和下午2:30-4:30。要求被试在指定路线上驾驶实验车辆，实时采集车辆的运动状态和周围环境状态参数。

实验车为一辆装配了毫米波雷达、速度传感器、视频影像传感器、GPS等设备的1.6 L排量的自动挡轿车。毫米波雷达及视频影像传感器主要记录所感知到的周围车辆的相对距离、相对车速等交通数据信息。车辆信息数据采集系统主要由传感器采集车速、制动开度等运动参数。工控机将各路信号集中并转换，实现数据信号的同步输出。

1.2 数据预处理

实验采集数据涉及两路信息源，分别是自车轨迹数据和车辆周围环境数据。具体包括：自车速度、制动开度、横摆角速度、与前车相对距离等，对上述直接输出的数据进行处理，可以获得后续分析所需其他数据。最终获取的行车轨迹参数如表1所示。

表1 行车数据特征指标Table 1 Characteristics for driving data

跟车工况标定通过视频查看，雷达、车辆信息采集系统数据分析共同确定。通过视频，人工筛选交通流稳定状况下的行车数据段，根据采集的自车轨迹数据和周围交通状况数据，标定跟车工况下的行车数据段。基于既有研究[9]，本文跟车工况提取规则设定如下：跟车距离100 m以内或跟车时距小于6 s；自车速度高于10 km·h-1；跟车时长不低于20 s，累计提取2000 余组跟车工况下行车数据，平均跟车时长40 s。

2 驾驶人跟车参数的差异性分析

2.1 理论方法分析

现有研究表明，不同驾驶风格的驾驶人在跟车时，其速度控制、跟车间距等表现出明显差异性，继而根据其参数分布区分驾驶风格。传统区分准则主要根据数据统计上的百分位值设定有效区间，缺乏个体数据时域和频域的深度挖掘。本文就驾驶人跟车参数的统计域、时域和频域特性进行多尺度分析。具体方法如下。

(1)统计域分析

跟车参数统计域分析主要基于轨迹数据，分析其均值、标准差、中位值、最值等，参数是否存在显著差异性一般采用方差检验等方法，对于不满足正态分布条件的数据，一般采用非参数Kruskal-Wallis H检验。

平均值为

式中：i为样本个体；xi为参数指标；n为总样本数。

标准差为

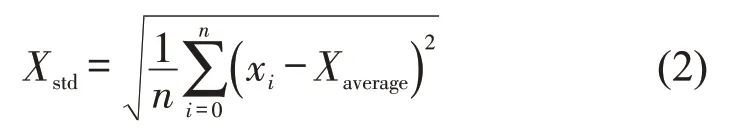
最大值为

最小值为

K-W检验的基本步骤为，将数据转化为秩统计量，计算各组样本平均秩来确定检验统计量H值并矫正Hc，进而查表获得P值进行检验。H值计算公式为

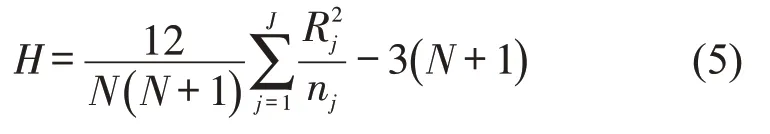
式中：N为每组样本的样本量；Rj为第j组样本的秩和；nj为第j组样本的观测值；J为样本组数。

(2)频域分析

傅里叶变换是一种典型的频域分析方法。它能将满足一定条件的某个函数表示成正弦基函数的线性组合或者积分。本文采用离散傅里叶变换(DFT)。具体算法为

式中：x(k)为L点离散傅里叶变换后的数据；x(l)为原始信号序列；L为周期采样点数；l为采样点；k为频率参数。

(3)时频分析

小波变换是时间频率的局部化分析，通过伸缩平移运算对信号逐步进行多尺度细化，最终达到高频处时间细分，低频处频率细分，能自动适应时频信号分析的要求，从而可聚焦到信号的任意细节。

对任意信号f(t)，若r0为任意一起点，定义f(t)的小波级数展开为

式中：t为时间参数；r为尺度参数，r≥r0；s为小波的位移系数；cr0(s)、dr(s)分别为近似系数、细节系数。当尺度函数φr0,s(t)和小波函数ψr,s(t)正交，那么近似系数cr0和细节系数dr计算公式为

2.2 数据分析结果

(1)统计学差异

驾驶人跟车行为特性主要体现在车速控制和车间距保持上，故本文选择加速度a、与前车相对速度ΔV、相对距离D、跟车时距XTHW、碰撞时间倒数XTTC,i等参数，分析其在统计域上的差异性。图1为8 名被试驾驶轨迹数据均值和95%置信区间分布。

由图1(a)可知，8 位被试的加速度均值相差较小，主要原因是，跟车工况下车辆运动状态相对稳定，车辆速度变化较小。由图1(b)可知，8位被试的跟车相对距离均值分别为21.18，12.75，24.45，21.09，18.58，16.96，12.54，13.82 m，其中，3 号被试跟车距离均值最大，7 号被试最小，两者相差48.71%，表现出明显差异。在跟车工况下，驾驶人激进程度与跟车距离呈负相关性，由此能够得出，2、7、8 号被试跟车更为激进，1、3、4 号被试则较为谨慎。激进驾驶人XTTC,i一般比谨慎驾驶人更大，图1(c)中XTTC,i均值表现出相应趋势。由图1(d)、(e)可知，8 位被试XTHW均值差异最大为52.88%，ΔV均值差异最大为245.55%。此外，8 位被试跟车参数的置信区间分布不尽相同，且各区间之间存在一定间距，表明被试跟车习惯存在差异。

为进一步探究各参数的差异性，选取均值、标准差、中位数等特征构建特征集，并进行K-W显著性检验。结果显示ΔV和XTTC,i的中位数Sig 值分别为0.011 和0.647，大于0.01，表明两者无显著差异，其他特征Sig值均小于0.01，存在显著差异。由此表明，驾驶人存在独特的跟车行为。

(2)频域差异

图2为经离散傅里叶变换后的8 位被试的加速度频谱图，可知，各被试加速度频率特性趋势相似，但仍存在细小差异，可用来分析驾驶人的行为特性。

图1 行车参数均值和95%置信区间Fig.1 Means and 95%confidence intervals of driving parameters

在跟车工况下，由于两车行驶状态较为稳定，加速度变化缓和，故在高频成分幅值不会太大。低频段高幅值特性表明各被试在跟车过程中车速变化较为平缓。从图2中可知，被试1、2、3、7 在1 Hz以后加速度幅值较小，被试4、5、6、8在高频段3 Hz 以后略大。高频段幅值越大，车速变化越剧烈，表明被试4、5、6、8在跟车过程中存在较为频繁的急变速行为，从侧面反映其对车速控制较差。

(3)时域频域差异

本文采用sym5 小波基对所选参数做5 层离散小波变换，提取每层小波系数(小波系数表示函数在特定频域上与信号的相似程度)。以加速度数据为例，随机抽取2位被试的1组跟车数据，重构结果如图3所示，图中d1～d5为各层细节系数，a5为第五层近似系数。

由图3可知，两位被试的小波系数在不同频段下的振幅变化存在差异。1号被试的第1层细节系数振幅在-0.2～0.2 之间，变化较小，表明该被试跟车过程相对稳定；4 号被试第一层细节系数变化在前20 s 相对稳定，在20～30 s 间振幅变大，数值在-0.5～0.5之间波动较大，表明加速度在该时刻变化较大，因此，小波变换可以放大某一局部特征，发现信号中细微的异常。

为进一步分析小波系数的内在规律，选取3位被试的加速度数据，进行小波变换，并绘制各层系数直方图，如图4所示。

从图4发现，3 位被试近似系数a5分布模态不同，1号被试呈现右偏双峰状态，2号为单峰状态，3号为左偏状态。三者各层细节系数频率分布也存在明显差异。

图2 加速度频谱图Fig.2 Spectrum diagram of acceleration

3 驾驶人个体差异性辨识模型

3.1 特征参数

上述分析发现，自车加速度、与前车相对距离、相对速度、跟车时距、碰撞时间倒数等参数在其统计分布和时频分布上具有不同程度的差异性，因此，将不同参数的统计域和时域、频域特征作为驾驶人个体差异性辨识的输入。在统计域，采用平均值、标准差、中位数作为特征输入。

根据对驾驶人跟车的时频分析，考虑到小波能量熵反映小波系数内部混乱程度，熵值越小，表明信号越稳定，驾驶人跟车行为越稳健，计算各系数的能量熵作为频域特征输入。小波能量熵计算公式为

式中：K为小波变换的分解层数。

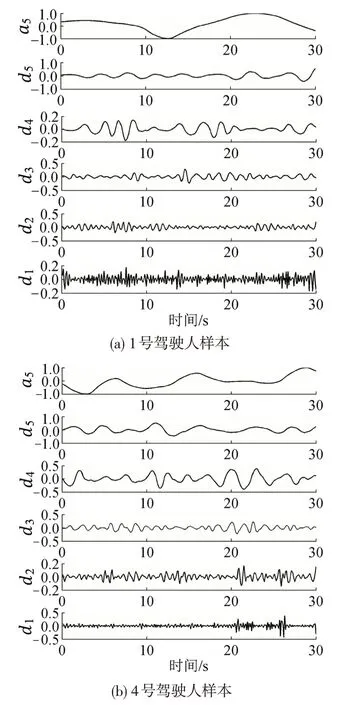
图3 加速度小波系数重构Fig.3 Wavelet coefficient reconstruction for acceleration

综上，模型待选参数为：X={a,D,ΔV,XTHW,XTTC,i} ，其参量特征为XEs，Xavg，Xstd，Xmid。

3.2 基于随机森林的辨识模型设计

采用随机森林对驾驶人差异性进行辨识。由于子决策树个数、样本最小叶子数等参数影响随机森林模型的分类效果，故需对模型参数进行最优化调整。调优算法使用贝叶斯优化(Bayesian Optimization)，根据先验信息设置各参数调优范围，使用10折交叉验证得到精度均值最大作为优化目标，获得模型的参数最优化结果，如表2所示。

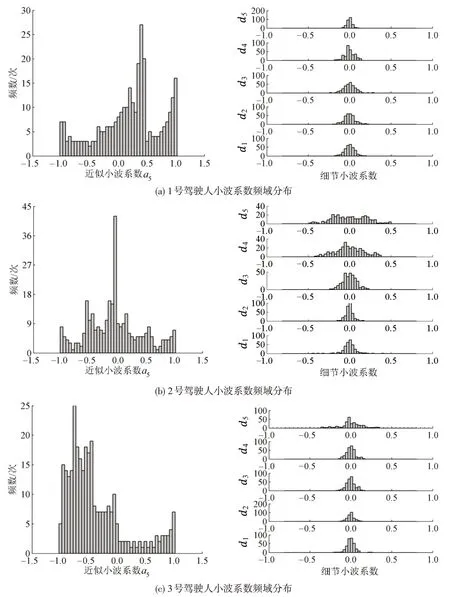
图4 加速度小波系数分布直方图Fig.4 Histogram of acceleration wavelet coefficient distribution

表2 基于贝叶斯优化的随机森林算法结构优化Table 2 Optimal results of random forest based on Bayesian optimization

模型识别效果分析中，引入3 个重要指标：计算精度P、召回率R、袋外错误率(OOB error)。精度可以显示预测正确的样本比例，召回率可显示预测指定驾驶员的比例，袋外错误率用以验证模型优劣。在模型随机采样阶段每次约有1/3的样本不会出现在采样集合中，即没参加决策树的建立，这些数据被称为袋外数据，故可以将袋外数据视为测试集进行分类，得到的误差率即为袋外错误率。

若将某一待识别驾驶人视为正类，其余驾驶人视为负类，则TP为样本中正类判定为正类的数量，FP为负类判定为正类的数量，FN为正类判定为负类的数量。

3.3 模型结果和分析

为了解不同特征参数组合对随机森林模型的影响程度，确定驾驶人差异性辨识最优特征参数，分别选取不同的特征指标作为输入，通过10 折交叉验证进行准确率评估。同时，采用支持向量机、K 近邻、BP 神经网络算法对不同参数组合进行识别，以对比不同机器学习方法的识别效果，结果如表3所示。

表3 不同参数输入的模型识别结果对比Table 3 Model comparison results with different inputs

从表3中可以看出：

(1)仅选择加速度作为输入参数，各模型的识别准确率较低，因为单一加速度特征并不能完全反映驾驶人的跟车特性。随着跟车行为参数的增加，模型识别准确率呈现不同程度的提高。总体上RF的识别效果要优于其他机器学习算法，以向量5作为输入时，识别准确率最高。

(2)以向量4 作为输入，RF 识别准确率为92.97%，相比向量3，准确率略有下降，表明跟车时距与其他参数存在一定的相关性，特征之间的相关性影响模型的性能。

(3)当考虑碰撞时间倒数XTTC,i后，即以向量5作为输入时，RF 模型识别准确率提高到96.81%，表明相比于跟车时距XTHW，XTTC,i更能有效地识别驾驶人，主要原因是XTTC,i更能体现驾驶人的距离感知特性，能够更直观地表征驾驶人跟车的激进程度。

(4)以向量6 作为输入参数，RF 识别准确率为95.21%，仅考虑与前车相对运动关系参数，己能取得较好的辨识结果，表明在特定工况下实现驾驶人辨识的可行性。同时考虑加速度及与前车相对运动关系参数，即以向量5 作为输入，识别准确率最高，为96.81%，因此选择向量5 作为最终的模型输入。

基于上述设计的随机森林模型对8 位被试进行辨识，总体识别准确率为96.81%，袋外错误率为4.55%，与现有基于统计特征的驾驶人辨识相比，准确率有较大提升。为进一步分析模型性能，采用精度和召回率对其进行评价。混淆矩阵如表4所示，其中，精度为96.4%，召回率为96.38%，均取得较高水平，表明模型分类辨识效果较好。

表4 模型识别混淆矩阵Table 4 Confusion matrix of model identification

4 结论

基于实验数据，分别从统计域、频域、时频域对驾驶人跟车轨迹参数展开分析，多尺度探讨驾驶人跟车行为差异性。结果显示，在跟车工况下，加速度、与前车相对距离、相对速度、跟车时距、碰撞时间倒数等参数能不同程度表征驾驶人的跟车特性，且不同驾驶人行车参数的统计域分布与时频域分布存在不同程度的差异性。

将跟车轨迹参数的平均值、标准差、中位数、小波能量熵作为特征参数，建立基于随机森林的驾驶人个体差异性辨识模型。结果显示，相较于其他机器学习模型，以加速度、与前车相对距离、相对速度、跟车时距、碰撞时间倒数为特征向量的随机森林辨识模型具有更好的辨识精度，识别准确率可以达到96.81%，在召回率、精度等方面也体现出较好的性能。

本文在驾驶人数据采集上存在一定局限性，算法对驾驶人辨识的敏感性还需要进一步分析，但本文研究初步表明，基于多尺度特征向量的随机森林分类方法在识别驾驶人跟车差异性上是可行的，可以为驾驶人身份识别，驾驶人非常态驾驶行为辨识等提供理论指导和方法支持。