设计变式练习,提升小学生数学核心素养
范 玲
(江苏省南通市五山小学,江苏南通 226001)
引 言
对于变式练习来说,它能更好地培植学生的思维能力,能让学生发现“多变”之中的“不变”,进而更好地形成相关的素养。一般来说,变式练习又分为问题变式、情境变式、方法变式等,旨在减少学生重复的、机械的、低效的训练,在呈现多种有变化的习题情境中,让学生顿悟数学、顿悟数感、顿悟实践、顿悟思维等[1]。
一、设计变式练习,反拨测试反馈
测试对小学数学学习是非常有必要的,它能反映出教师的教学情况,也能体现出学生的学习状况[2]。一般来说,教师可利用测试来调整自己的教学方法、教学内容、教学进度等,以适应学生在测试中显露出来的学情。教师的调整主要是在修正学生错误的同时,以变式的方式来巩固相关的认知,再向深一层的思维漫溯。变式的目的就是检测学生能不能做到知其一,也知其二;就是让学生从多个维度掌握相关认知。传统的教学总是让学生对同一题目进行反复训练,以让他们记住,但这样做的缺点在于学生在其他方面的思维能力没有得到锻炼。一旦换了新的情境,学生就不会解题了。
以苏教版小学数学三年级上册“认识几分之一”这一章节为例,教师在测试中设置这样一道题:“观察这幅黑板报的版面(见图1),能用所学的分数说一说,谁占谁的几分之一吗?即“科学天地”栏目大约占黑板报版面的几分之几,“艺术园地”栏目大约占黑板报版面的几分之几。”设置这道题的目的是让学生结合具体情境初步认识分数,进而让他们知道把一个物体或一个图形平均分成几份,每份都可以用几分之一来表示。教师从熟悉的事物入手,让学生在感受数学与生活的联系的同时,产生了对数学的好奇心和兴趣。在测试中,有的学生把“科学天地”看成了整个黑板报的三分之一,而把“艺术园地”看成整个黑板报的三分之一。这说明学生在将一个物体进行划分时,还没能真正弄清楚每一事物所占的份额。于是,教师可在同样的问题情境中,变式方法,以让学生再做一次思考,题目为:“同学们想在‘科学天地’中再设置一个‘小发明’栏目(见图2)。那么,‘小发明’栏目大约占‘科学天地’的几分之几,‘小发明’栏目大约占整个黑板报版面的几分之几。”可见,基于测试的变式,旨在对接学生的最近发展区,以让学生的相关能力得到拓展,也最大可能地发挥了测试的功能。

图1
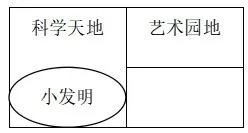
图2
二、设计变式练习,优化教学方式
当前,小学数学实施的是核心素养教育,让学生各方面的能力得到充分发展。教师要不断地优化教学方式,以给学生最适切的生长。教学方式要能体现学生的主体地位,让每位学生都参与到学习中,即要让课堂变成自学、互学、展学等环节,而不是一味地以教师讲解为主的“师本”课堂[3]。
以苏教版小学数学六年级下册“解决问题的策略——转化”这一章节为例,教师先是设置了这样的一道题:“一杯含盐率为12%的盐水(重200 克),往这杯盐水中加入20 克盐、80 克水。这杯盐水是变淡了,还是变浓了?”教师先让学生对问题进行转化,变淡还是变浓其实就是含盐率,即盐占盐水的百分比。同时,学生还要将题目的内容进行转化,即相同质量的盐加入不同质量的水会有这样的结论:加水越多,含盐率越低,即越淡;反之,加水越少,含盐率越高,即越浓。由于缺乏生活经验,学生对这样的题目还有一定的理解困难。因此,教师要改变问题情境,设置变式练习,题目:“买来蘑菇10 千克,含水量为99%。晾晒一会儿后,蘑菇的含水量为98%,问蒸发掉多少水分?”教师将学生分成不同的小组,让每个小组都分得一份蘑菇。教师也将每份蘑菇的质量告诉了学生。这些蘑菇被放到太阳下晒了15 分钟。教师让学生注意观察,以发现一些问题。学生观察到蘑菇中的水分在阳光下蒸发了,进而知道蘑菇有水分这一事实,也知道了干蘑菇的重量不变这一事实。学生在小组中讨论,认为可根据干蘑菇的重量不变,求得10×(1-99%)=0.1(千克);再根据晾晒后含水量为98%,列出这样的式子:含水量为98%的蘑菇有0.1÷(1-98%)=5(千克),求得蒸发掉的水的重量。最后,教师让学生以小组为单位讨论得出:含水量问题其实就是盐水问题和浓度问题。换言之,变式练习就是要让学生看出其中的变与不变,进而以不变应万变。教师在设置这样的变式练习时,应充分尊重学生的主观能动性,让他们自己去找寻浓度问题中的不变量。换言之,教师要让学生体会“变”的是什么,“不变”的又是什么,这些“变”与“不变”之间的关系又是怎样的。
三、设计变式练习,提升思维品质
数学学习的过程也是学生思维品质生长的过程。在小学数学教学过程中,教师要关注学生思维的生长,让他们克服原有的思维短板,以促进各方面能力的发展[4]。而在当前的数学教学中,很多教师不重视学生思维品质的培养。当学生成绩不好时,教师加大训练力度来提升他们的成绩,导致学生陷入题海战。教师要抓住题目的本质和学生的思维特点,设置变式练习,以达到事半功倍的效果[5]。
以苏教版小学数学三年级下册“有趣的乘法计算”为例,教师先出示题目:24×11;53×11,问学生一个两位数和11 相乘的得数有什么共同的特点。有位学生说出这样的特点:“24×11=264,所得的积个位上的数,与原来两位数个位上的数一样,都是4;积百位上的数,与原来两位数十位上的数一样,都是2;积十位上的数,等于原来两位数个位与十位上数的和,即2+4=6。”其他学生不需要教师提问,就自己在下面说开了。教师让一排学生每人说一句。第一位学生说:“3×11=583,所得的积个位上的数,和原来两位数个位上的数一样,都是3。”第二位学生说:“积百位上的数,与原来两位数十位上的数一样,也都是5。”第三位学生说:“积十位上的数,等于原来两位数个位与十位上数的和,即5+3=8。”学生的思维得到锻炼。最后,教师让学生自己来设置变式练习,以检验刚才的发现。这次变式是基于问题的变式,是让学生成为设计变式的主人,不再是教师引领着走。对学生来说,让他们自己设置变式,就是对他们思维能力的又一次挑战,因为他们要看清哪些是不能变的、哪些是可以变的。学生很快就想出这样的题目:62×11。学生还在再次的训练中得出这样的结论,即“两头一拉,中间相加”。变式训练与思维对接,数学素养就油然而生。
结 语
核心素养培养的目的是促进学生的全面发展,是让他们掌握核心能力。变式练习能让学生从繁重的课业中解放出来,无论在认知上还是在能力上,都会获得更多成长的机会。教师在变式练习的设置上要注重面向全体学生,对接学情,关注能力,引领他们全员参与。当变式练习成为核心素养的催化剂,学生就会成为变式练习的受益者。

