基于单-双高斯模型拟合法的测风激光雷达海上风电机组尾流特征分析

刘清媛,吴松华,2,3∗,张凯临,3,李荣忠,3,翟晓春

(1 中国海洋大学信息科学与工程学院,海洋遥感研究所, 山东 青岛 266100;2 青岛海洋科学与技术试点国家实验室,区域海洋动力学与数值模拟功能实验室, 山东 青岛 266237;3 青岛镭测创芯科技有限公司, 山东 青岛 266101)

0 引 言

近年来,随着绿色低碳转型政策的深入推进,新能源装机和发电比重进一步上升,风能作为一种清洁的可再生能源,受到了人们的广泛关注。国家能源局报告指出,截至2019 年9 月底,我国风电装机容量达到1.98 亿千瓦,风电发展进入了快车道。我国领土广阔,风能资源丰富,有利于大型风电场的建设和并网发电。在风电场中,风电机组的发电效率受到大气风场环境和邻近风电机组尾流效应的影响,对风电机组尾流的观测和研究有利于优化风电机组布局,实现风电场经济效益最大化。

目前风电行业对风电机组尾流的研究大致分为三类: 尾流模型研究、数值模拟研究和基于实测数据的实验研究。其中尾流模型和数值模拟研究较为成熟, 并且普遍应用于风电场的数据分析工作中。Jensen[1]提出的一维线性尾流模型(Park 模型)能较好地模拟平坦地形的尾流情况,是目前风能资源评估软件WAsP 中使用的尾流模型。Lissaman[2]在实测数据的基础上提出针对风电机组高低位置不同的尾流模型。Ainslie[3]提出涡黏性尾流模型,采用轴对称坐标下N-S 方程求解计算尾流速度亏损场。Larsen 模型是半解析性模型,由Prandtl 旋转对称湍流边界层公式推导得出[4]。张晓东、张镇[5]结合适用于近场尾流分析的无黏尾流模型和修正后更适用于远场尾流分析的Jensen 模型建立全场尾流模型,提高尾流模型分析的可靠性和真实性。杨祥生等[6]在传统Park 模型的基础上提出的Park-Gauss 模型可以很好模拟尾流区的风速,不仅在精度上与试验结果接近,还能分析尾流横向的径向风速分布特征。Nedjari 等[7]利用CFD 对复杂地形和平坦地形下的风机尾迹演化进行研究,CFD 在一定程度上可以模拟风电机组周围复杂流场。大气风场复杂多变,风电机组的偏航、变桨对下风处尾流产生一定影响,运用声雷达、多普勒测风激光雷达等新型测风设备可以对真实风电场中的风电机组尾流进行观测和研究。H¨ogstr¨om 等[8]利用高分辨率的声雷达分析了尾流区2 D～4 D 范围内的风速廓线和湍流结构。Krishnamurthy 等[9]通过扫描型多普勒激光雷达对海上风电机组尾流进行探测,获取了尾流中心风速和自由流场风速数据计算风速损失率。中国海洋大学Feng 等[10]运用两台脉冲相干多普勒激光雷达对潮间带风电场风电机组尾流进行同步观测,分析了尾流区小尺度的大气运动和尾流扩散运动。中国海洋大学于晓庆、吴松华[11]运用脉冲相干多普勒激光雷达在新疆风电场开展风场探测实验,利用单高斯拟合算法处理尾流风速数据,并分析了尾流特征参数。

在尾流模型和数值模拟研究过程中,通过改进尾流模型和模型叠加等方式可提高尾流特征研究的准确性。在基于实测数据的实验研究过程中,在不同风电场开展风场探测实验,从实测数据中提取尾流特征参数,部分学者采用单一高斯拟合模型处理尾流横向的速度,没有将高斯拟合算法细化。Magnusson[12]通过理论计算和测量结果提出在尾流形成初期,由于叶轮对气流的切割作用,中间机舱对气流的影响相对较弱,尾流横向风速呈双高斯分布,随着尾流扩散距离的增加,尾流横向风速逐渐呈单高斯分布。因此,仅运用传统单高斯拟合算法处理风电机组的尾流风速数据,对紧邻风电机组的尾流风速分析存在误差较大的情况。本文提出一种单–双高斯拟合算法,结合单高斯拟合与双高斯拟合对风电机组尾流数据分析的优势,对传统单高斯拟合算法进行改进,修正拟合误差较大的结果。在江苏某海上风电场开展风场探测实验,通过对尾流宽度、风速损失率、尾流长度和尾流中心位置等尾流特征分析,验证了单–双高斯拟合算法的可行性和准确性。

1 算法原理

运用相干多普勒测风激光雷达获取海上风场的径向风速信息,通过VAD(Velocity azimuth display)风场反演算法可以得到真实风场的主风向和背景风速,可以进一步获取目标风电机组的尾流数据;运用高斯拟合算法可以实现尾流垂直截面上横向风速数据的拟合分析,从而获取尾流特征参数。

1.1 VAD 风场反演算法

在相干多普勒测风激光雷达实测数据处理过程中,假设不同高度大气风场是均匀的,选取同一高度上的径向风速数据,通过正弦拟合得出激光雷达径向风速随方位角的变化信息,该方法为VAD 风场反演方法[13],其表达式为

式中: y 为水平风速, x 为激光雷达的扫描方位角, A、φ 为计算真实风场的风速和风向的拟合参数。以图1拟合数据为例,径向风速最小值ymin对应横坐标的激光雷达扫描方位角约为297◦,此时风场主风向为东偏南风,径向风速最大值ymax计算风场的背景风速为6.2 m·s−1。

图1 VAD 风场反演算法拟合曲线Fig.1 Fitting curve of VAD wind field inversion algorithm

1.2 高斯模型拟合算法

定义主风向为风电机组尾流的纵向,尾流沿纵向扩散,尾流横向上的风速为水平并且垂直于主风向的风速。对尾流横向风速进行高斯拟合之前,需将尾流区分成若干个垂直截面,获取每个垂直截面的横向风速,对每一组尾流风速进行高斯拟合处理。

1.2.1 单高斯拟合式(2)为单高斯拟合函数,式中: uLOS为尾流垂直截面的横向风速,u 为高斯函数的拟合参数,表示尾流垂直截面外自由流场风速,a0为拟合函数最大值与最小值之差,b0为高斯拟合峰值所在位置,即对应尾流中心的位置,c0为高斯拟合函数的标准差。根据定义,单高斯拟合计算的尾流中心风速为uwake= u −a0,风速损失率的计算公式为

单高斯函数的标准差c0是计算尾流宽度的重要参数,定义95%置信区间为尾流宽度,尾流宽度[14]约为

1.2.2 双高斯拟合

在尾流形成初期,由于叶片对两边气流的切割作用和中间机舱的存在,造成尾流横向风速值呈双高斯分布,传统尾流模型算法认为尾流横向风速分布为双峰对称的双高斯线型,即双高斯拟合函数的左右标准差相同。对于工作状态的风电机组而言,来流风向与风电机组扫风平面的夹角和风电机组自身变桨都将影响叶片后方尾流风速分布和尾流大小,导致尾流中心两边的风速损失不均,紧邻风电机组尾流垂直截面上风速分布是不对称、不规则的双高斯线型,因此对传统对称双高斯模型做出改进,具体的表达式为

式中: a1、a2分别为双高斯函数中两个峰值与自由流场风速的差值,b1、b2分别双高斯拟合两个峰值所在位置,c1、c2分别为左右高斯线型标准差。双高斯拟合定义尾流风速为uwake= u −max(a1,a2),风速损失率和尾流宽度计算公式分别为

图2 为对单个尾流垂直截面上尾流横向风速进行单高斯拟合和双高斯拟合的对比结果,横坐标为尾流横向距离,用几倍叶轮直径n D(D 为风机机组叶轮直径,下同)表示,纵坐标为尾流横向风速。

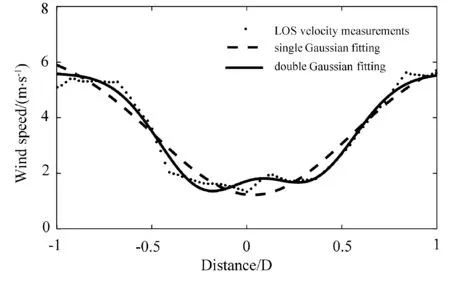
图2 单高斯拟合与双高斯拟合结果对比Fig.2 Comparison of single Gaussian fitting and double Gaussian fitting results

1.3 单–双高斯拟合算法实现

单–双高斯拟合算法在传统单高斯拟合的基础上,对单高斯拟合进行改进,同时加入双高斯拟合算法,对单高斯拟合精度不足的单个尾流垂直截面数据进行修正,提高拟合精度,减小拟合误差,单–双高斯拟合算法流程如图3 所示。

1)首先将风速数据进行归一化处理,根据式(2)对参数进行初始化: u 定为尾流横向上的最大风速;a0为尾流横向风速最大值与最小值之差;b0为初始化尾流中心位置,设为0;令初始尾流宽度为D,c0为尾流宽度的1/4,即0.25 D;令p 为均方根误差,当p ＞0.25 时,清空初始值,对该组数据再次进行单高斯拟合。

2)通过实测数据预处理与分析,定义单高斯拟合误差q ＞0.2 或尾流宽度大于3 D 时,采用双高斯拟合对该组尾流风速重新处理。双高斯拟合均方根误差小于0.1,尾流宽度小于3 D 时拟合结束,输出拟合参数。对于拟合均方根误差无法小于0.1 的情况,通过循环拟合,选取最小拟合误差的结果进行后续尾流参数计算与分析。

图3 算法流程图Fig.3 Flow chart of algorithm

2 实验设置与数据分析

2.1 实验设置

中国海洋大学激光雷达团队于2017 年10-11 月在江苏某海上风电场开展风电机组尾流观测实验,实验期间平均风速为6.29 m·s−1,激光雷达与目标风电机组的轮毂中心相对高度为73.6 m,水平距离为663 m。

相干多普勒测风激光雷达利用光的多普勒效应实现大气风场探测,激光器发出的激光束与气溶胶粒子相互作用产生回波信号,回波信号光与本振光在探测器表面混频得到多普勒频移,由多普勒频移即可得到探测范围内的径向风速[15]。实验采用相干多普勒测风激光雷达的PPI (Plane position indicator)扫描模式进行风电机组尾流探测,PPI 模式是固定俯仰角,改变方位角的探测方式,根据实验的需求设置方位角和俯仰角的范围[16],数据反演结果是以激光雷达为中心的极坐标扇形图(如图4),色标颜色深浅表示径向风速大小,风向与激光出射方向相同时,风速为正值,反之风速为负值。

本次实验设置PPI 扫描方位角为263◦～360◦(如图5 所示),俯仰角为1.0◦～3.6◦,本次实验数据处理过程中主要分析探测俯仰角为3.4◦的尾流数据,相干多普勒测风激光雷达的技术指标如表1 所示。

图4 PPI 扫描模式(a)与风场反演结果(b)Fig.4 PPI scanning mode(a)and the inversion result of wind farm(b)

图5 多普勒测风激光雷达探测俯视图Fig.5 Top view of Doppler wind lidar detection

表1 多普勒激光雷达技术指标Table 1 Technical specifications of Doppler lidar

2.2 单–双高斯拟合算法分析

选取2017 年11 月6 日第一组尾流实测数据进行风电机组尾流的可视化分析,背景风场主风向为东偏南风, 结合风电机组的偏航信息,确定风电机组尾流的扩散方向。数据处理分析过程中, 主要研究尾流区0～5 D 范围内的速度场变化,把尾流区分成15 个垂直截面,每个截面距离为0.34 D。不同距离处的尾流垂直截面风速分布如图6 所示,横坐标表示尾流横向距离,坐标点(0,0)为初始尾流中心位置。从图中可以看出尾流形成初期,尾流中心风速值骤减,在0～2 D 距离内尾流风速损失较大,随着距离的增加尾流风速逐渐增大,尾流中心位置发生左右偏移。

图6 尾流垂直截面风速变化规律Fig.6 Variation of wind speed in the vertical section of wake

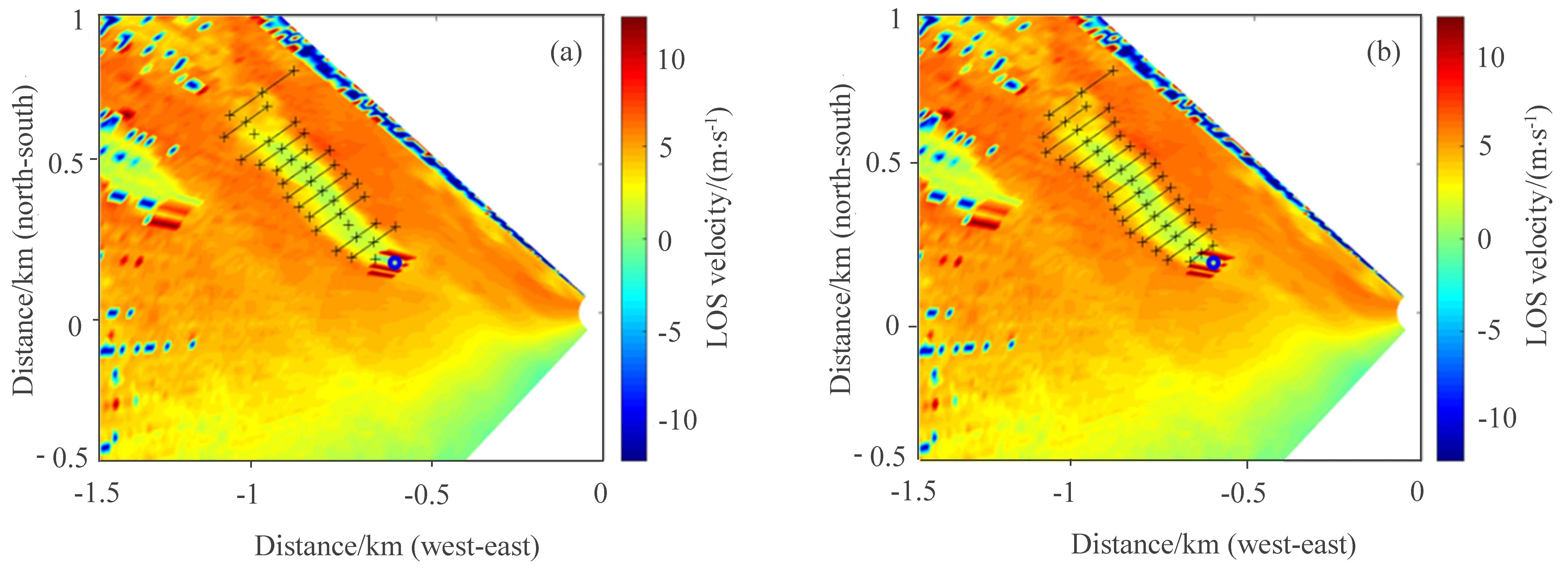
图7 风电机组尾流PPI 图。(a)传统单高斯拟合算法;(b)单–双高斯拟合算法Fig.7 PPI detection of wind turbine. (a)Traditional single Gaussian fitting,(b)single-double Gaussian fitting

如图7 所示,风电机组下风处5 D 范围内的尾流踪迹较为清晰,PPI 探测模式俯仰角为3.4◦的扫描平面接近尾流中心所在平面,本次实验选取风电机组下风处0～5 D 距离内的尾流特征参数进行分析。图7(a)为传统单高斯拟合算法的尾流可视化示意图,由于紧邻风电机组处尾流横向风速呈双高斯分布,用传统单高斯拟合算法提取尾流特征参数在个别尾流垂直截面存在拟合偏差较大的情况,如对第一、第二、第四个尾流垂直截面所示,由于拟合误差较大或者产生无效拟合数据,导致单个尾流截面可视化空缺和偏差,尾流宽度计算偏大。图7(b)为运用单–双高斯拟合算法进行尾流特征提取的可视化图,紧邻风电机组的尾流垂直截面中,单–双高斯拟合对拟合误差较大的结果进行订正,提高了尾流特征参数提取的有效性,从而保证了尾流特征数据的完整性。

图8 风速损失率对比分析。(a)传统单高斯拟合算法;(b)单–双高斯拟合算法Fig.8 Comparative analysis of velocity deficit. (a)Traditional single Gaussian fitting,(b)single-double Gaussian fitting

图8 为每个尾流垂直截面对应的风速损失率对比分析,横坐标为风电机组下风处距离,通常用几倍的叶轮直径表示(n D),风电机组尾流在3 D 距离内风速损失率较为平稳,平均风速损失率为83.27%,3 D 距离处开始风速损失率下降,在5 D 距离达到22.35%。如图8(a)所示,由于传统单高斯拟合算法将拟合误差较大的结果作为无效数据,影响后期风速损失率的统计分析。

图9 紧邻风电机组的尾流风速高斯拟合结果。(a)第一个尾流垂直截面(0.34 D);(b)第二个尾流垂直截面(0.68 D);(c)第三个尾流垂直截面(1.02 D)Fig.9 Gaussian fitting of the near wake of wind turbine. (a)The first wake vertical section(0.34 D),(b)the second wake vertical section(0.68 D),(c)the third wake vertical section(1.02 D)

选取07:11 探测的尾流数据作个例分析,前三个尾流垂直截面单高斯拟合和双高斯拟合结果对比如图9所示。由图9 可以看出,尾流速度损失具有明显的不对称性,随着距离的增大,尾流逐渐融合,因为风电机组叶轮对气流的切割作用,叶片后方尾流速度亏损较大。表2 为单高斯拟合和双高斯拟合对紧邻风电机组尾流数据的尾流特征拟合结果与误差分析,在紧邻风电机组处,双高斯拟合对尾流横向风速数据的拟合效果优于单高斯拟合。

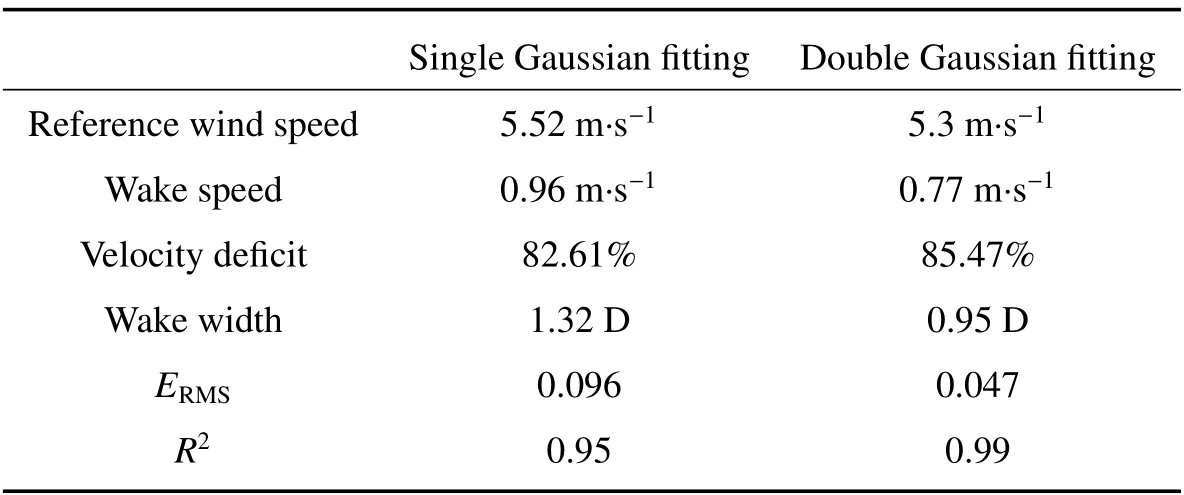
表2 尾流特征参数与误差指标Table 2 Wake characteristic and error index

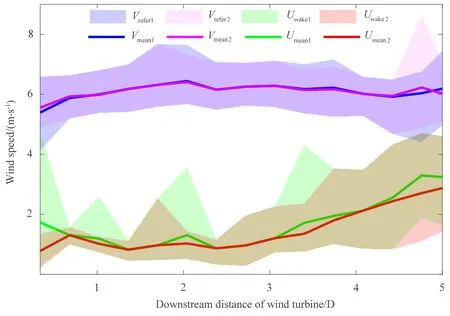
图10 传统单高斯拟合和单–双高斯拟合提取的参考风速与尾流风速对比分析Fig.10 Comparative analysis of reference wind speed and wake speed by traditional single Gaussian fitting and single-double Gaussian fitting

参考风速是尾流垂直截面横向尾流区外的自由流场风速;尾流风速是尾流中心处的风速值,通常情况下定义实测数据中,尾流横向最小风速值为尾流风速。根据式(2)和式(5)得到参考风速和尾流中心风速的计算参数,其中,参考风速为u,单高斯拟合提取的尾流风速为uwake= u −a0,双高斯拟合提取的尾流风速为uwake= u −max(a1,a2)。图10 为运用传统单高斯拟合算法和单–双高斯拟合算法提取的参考风速和尾流风速对比分析。其中,Vrefer1、Vmean1、Uwake1、Umean1分别为传统单高斯拟合算法提取的参考风速、平均参考风速、尾流风速、平均尾流中心风速;Vrefer2、Vmean2、Uwake2、Umean2分别为单–双高斯拟合算法提取的参考风速、平均参考风速、尾流风速、平均尾流中心风速。尾流区外的自由流场风速较为稳定,尾流形成初期,由于风电机组叶片对气流的切割作用,叶片后方湍流强度增大,气压骤减,尾流风速损失较大,随着尾流扩散距离增加,风电机组对下游尾流场的速度影响减小,尾流中心风速逐渐增大。图中可以看出,目标风电机组尾流区0～3 D 范围内,尾流风速小于2 m·s−1,从3 D 距离处开始尾流风速逐渐增大,在5 D 距离处尾流中心风速约为3 m·s−1。

通过平均绝对误差(Mean absolute error,MAE)可以评估传统单高斯拟合算法与单–双高斯拟合算法对尾流中心风速的计算偏差,其计算公式为

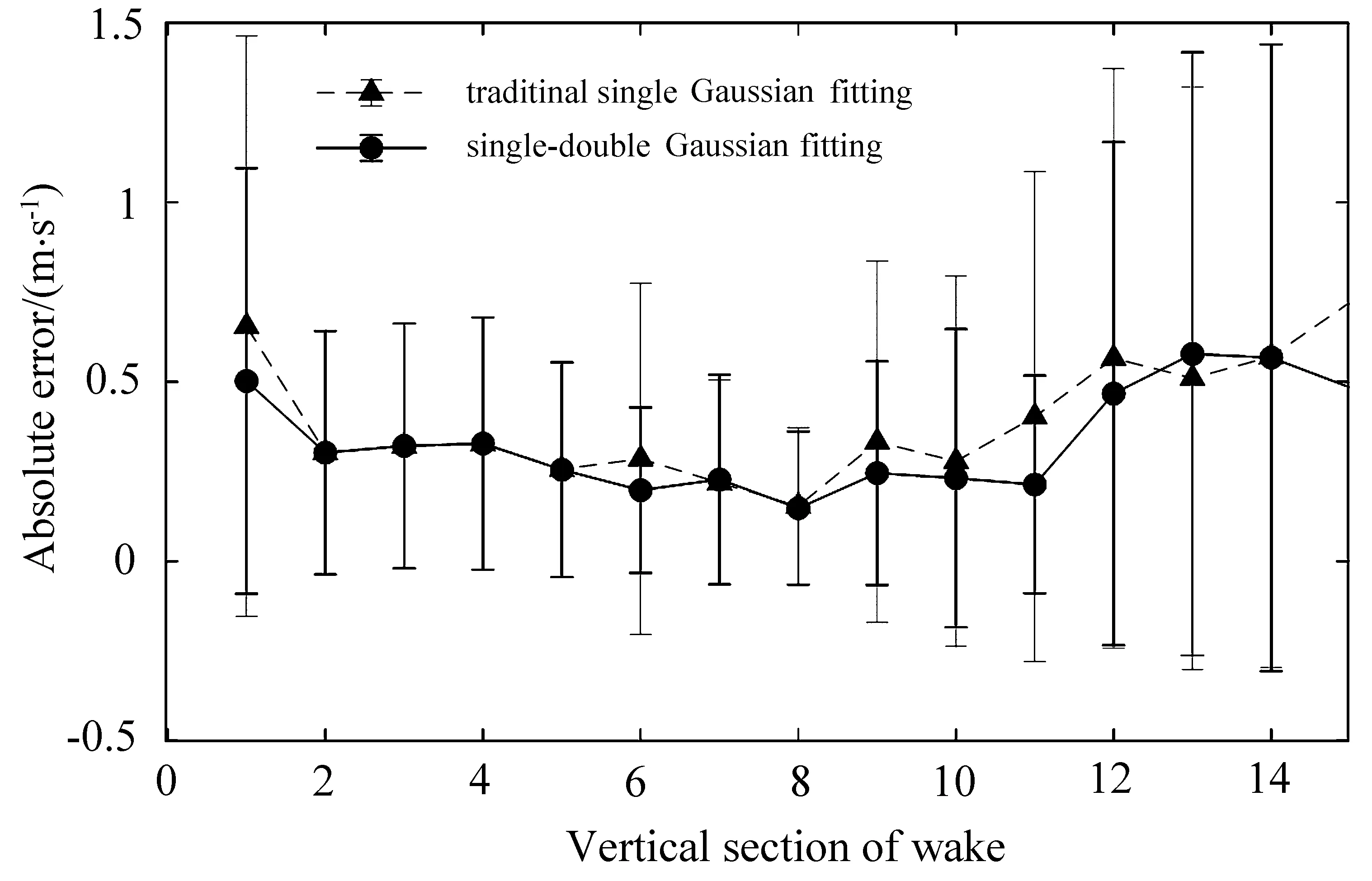
图11 尾流风速计算误差Fig.11 Calculation error of wake speed

图12 风速损失率统计分析Fig.12 Statistical analysis of velocity deficit

2.3 海上风电机组尾流特征参数分析

2.3.1 风速损失率分析

风速损失率随着尾流运动距离的增加而呈递减趋势,其计算方式参考式(6)。对00:11-16:47 时段的风速损失率进行统计拟合,结果如图12 所示,在尾流区0～2 D 范围内,风速损失率没有明显下降,反而有一定程度的攀升,根据上述尾流横向风速分布规律可知,此时尾流横向风速呈双高斯分布,在2 D 距离之后,风速损失率随着距离的增加呈缓慢减小的趋势。

实际探测过程中,尾流长度约为6 D～8.4 D。在海上风电场中,风电机组下风处3 D 范围内风速损失率没有明显下降,平均风速损失率为84.77%;在3 D 距离之后随着尾流中心风速不断恢复,风速损失率逐渐减小,6 D 距离处风速损失率为36.85%。定义风速损失率减小到10%时对应的距离为尾流长度,单–双高斯拟合算法估算的平均尾流长度为7.92 D,由于末端尾流风速逐渐与自由风场风速融合,越接近尾流末端,其风速损失率下降越缓慢。结合尾流实测数据可视化图与数据分析可知,在风电机组下风处距离大于8 D 时,尾流风速恢复自由流场风速,尾流效应减弱,尾流特性不显著,测风激光雷达无法观测这部分尾流特性。

2.3.2 尾流宽度分析

理想尾流模型假设尾流宽度随着距离的增加呈线性增大,尾流区呈圆台状。实际尾流观测实验显示,尾流宽度受到背景风速和大气湍流的影响,尾流宽度呈先增大后减小的变化趋势,表现为尾流边缘气流与背景风场气流混合。图13 为单–双高斯拟合算法计算的每个尾流垂直截面上的尾流宽度。尾流宽度的计算参考式(7),初始尾流宽度约为1 D,尾流区0～5 D 范围内的平均尾流宽度为1.42 D。在风电机组下风处0～2 D 距离内,尾流宽度逐渐增大,2 D 距离处平均最大尾流宽度为1.57 D。尾流运动距离大于2 D 时,尾流宽度随着距离的增大呈减小或波动趋势,尾流运动末端宽度约为尾流形成初期宽度的1.51 倍。

图13 风电机组尾流宽度统计分析Fig.13 Statistical analysis of wake width

通过单–双高斯拟合算法提取不同尾流垂直截面外的背景风速,尾流扩散过程受背景风场的影响,不同风速条件下,尾流风速损失率和尾流宽度存在差异性。以0～3 D 距离内的尾流特征参数为例,11 月6 日实验期间平均风速为6.7 m·s−1,平均风速约为5.5、6.5、7.4、8.8 m·s−1时,风速损失率分别为82.14%、85.53%、87.59%、86.41%,平均尾流宽度分别为1.35 D、1.49 D、1.52 D、1.48 D,如图14 所示,背景风速小于6 m·s−1时,风电机组尾流风速损失较小,平均尾流宽度较小。

2.3.3 尾流中心位置校正

在尾流模型和数值模拟研究中,风电机组位置固定,当气流经过风轮时,在其下游拖出的尾涡在空间上呈螺旋形涡线。在均匀大气条件下,若将尾流看成均匀的圆台状,则尾流中心为圆台中心,传统定义中尾流横向风速最小值所在位置为尾流中心位置。实际风场分析中发现,紧邻风电机组处,尾流横向风速呈双高斯分布,尾流中心为左后两个速度峰值位置中心;随着尾流的扩散,尾流横向风速呈单高斯分布,此时尾流中心为风速最小值所在位置。

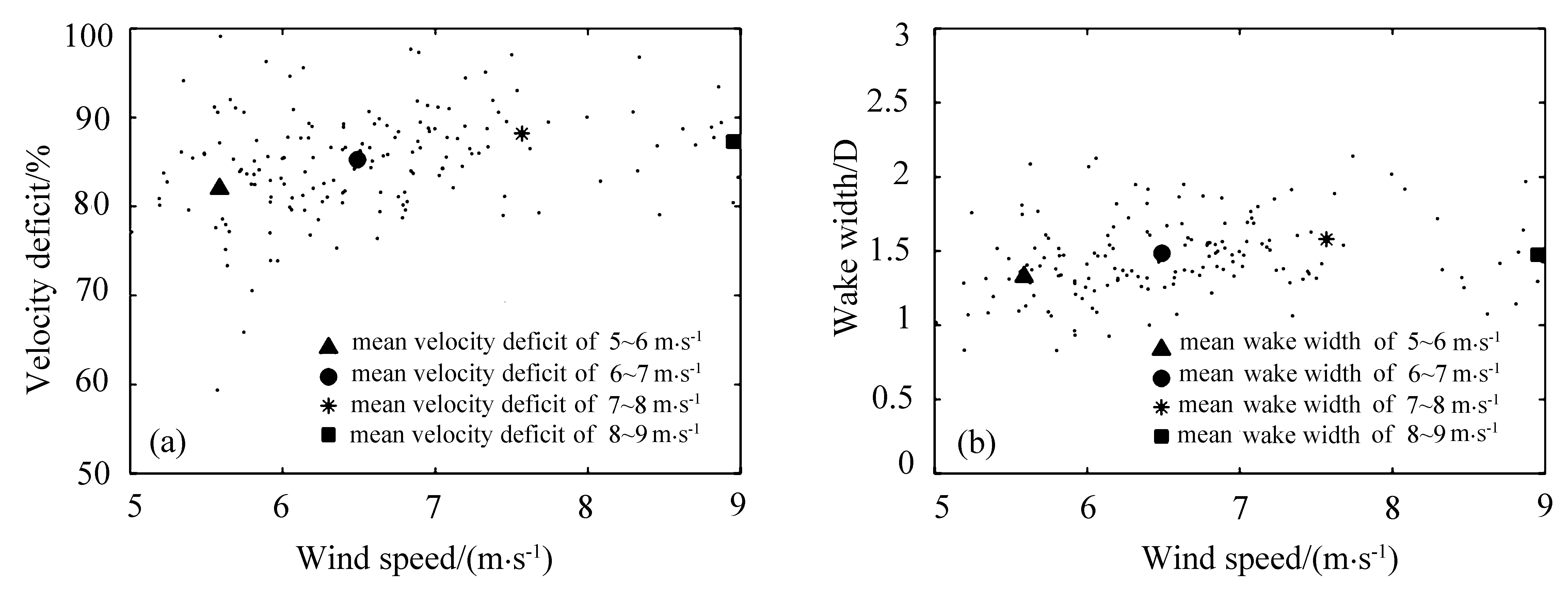
图14 风速损失率与背景风速的关系(a)和尾流宽度与背景风速的关系(b)Fig.14 Relationship between velocity deficit and background wind speed(a)and relationship between wake width and background wind speed(b)

图15 为2017 年11 月6 日07:11 的风电机组尾流数据个例分析。如图15(a)所示,在第二、第四、第六个尾流垂直截面的尾流中心位置存在一定偏差;如图15(b)所示,单–双高斯拟合算法对传统定义的尾流中心位置进行修正,对尾流中心位置计算较为准确。海上风场较为稳定,在风电机组尾流扩散过程中,0～5 D距离内的尾流中心不会出现较大的左右偏移,而在尾流末端(距离大于5 D)由于尾流中心风速逐渐恢复,尾流受周围自由流场的气流影响出现明显的弯曲变化。

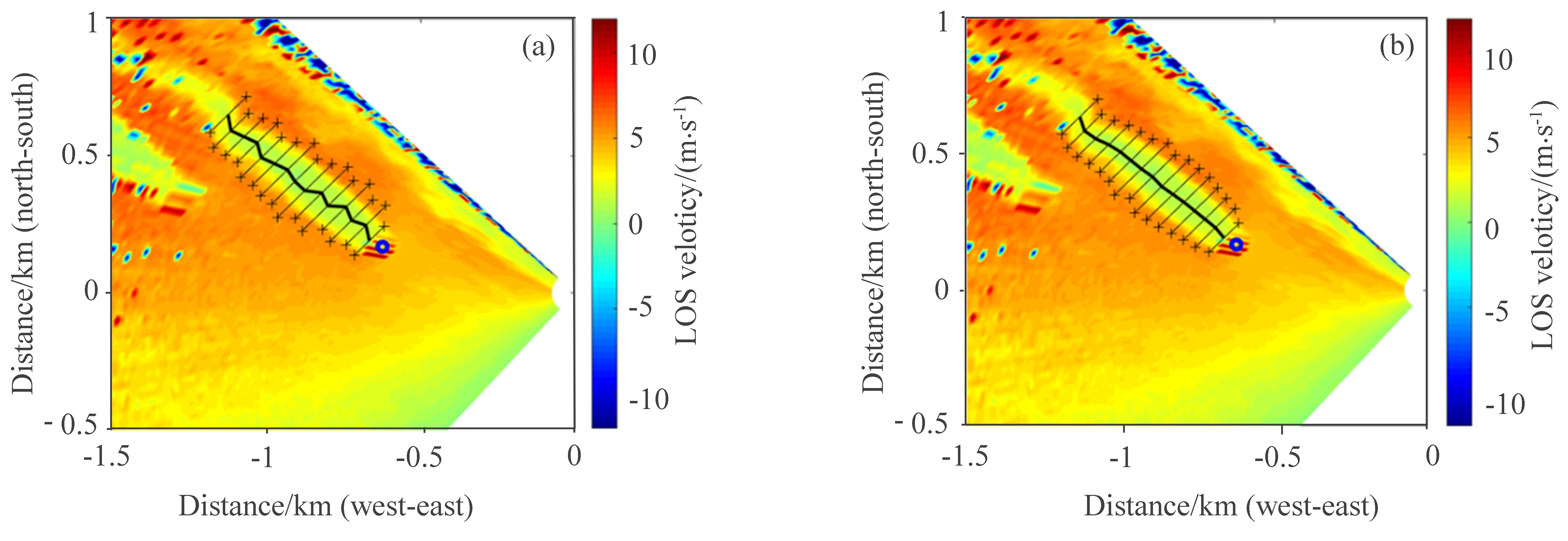
图15 修正尾流中心位置。(a)传统定义的尾流中心位置;(b)单-双高斯拟合计算的尾流中心位置Fig.15 Correction of wake center position. (a)Traditional single Gaussian fitting,(b)single-double Gaussian fitting

3 结 论

运用相干多普勒测风激光雷达在江苏某海上风电场开展了风电机组尾流观测实验,通过PPI 扫描模式对风电机组尾流速度场进行了可视化探测与分析。针对传统单高斯拟合算法拟合精度不足的问题,提出单–双高斯拟合算法订正单次拟合误差较大的数据,修正尾流中心位置,提高尾流特征参数分析的准确性,同时对海上风电机组尾流特征进行统计分析,实验观测结果显示:

1)由于风电机组叶轮对气流的切割作用明显,中间机舱对气流的影响较弱,气流经过风电机组扫风平面时,下风处气压骤降、湍流增强,紧邻风电机组叶轮的尾流横向风速呈双峰不对称的双高斯分布;随着距离增加,气压逐渐回升,尾流横向风速呈单高斯分布,尾流中心风速逐渐增大。传统单高斯拟合算法处理紧邻风电机组尾流横向风速数据出现拟合误差较大的情况,双高斯拟合算法处理紧邻风电机组尾流数据具有一定优势。本文提出单-双高斯拟合算法优化传统高斯拟合算法,对传统单高斯拟合算法进行参数优化,同时对单个尾流垂直截面拟合误差较大的结果进行修正,拟合曲线与实测尾流横向风速分布的相关系数可达到0.99,通过均方根误差和尾流宽度评估一组尾流横向风速数据的拟合结果,可以实现近尾流场的尾流特征参数的提取,提高尾流速度场分析的准确性。

2)在海上风电机组尾流特征分析中可知,在0～3 D 范围内风电机组尾流风速损失率较大,此时尾流宽度逐渐增加,背景风场风速为6.5 m·s−1时,平均风速损失率为85.53%,平均尾流宽度为1.49 D。3 D～5 D 范围内受周围大气风场影响,尾流中心风速逐渐增大,风速损失率逐渐下降,在5 D 距离处的平均风速损失率约为58.21%。在风电机组尾流扩散过程中,0～5 D 距离内的尾流中心无明显偏移。通过风速损失率的统计拟合分析可知,单-双高斯拟合算法估计尾流长度约为8 D,8 D 距离后尾流逐渐恢复成自由流场风速。