大气光学湍流廓线探测方法研究进展

王彩玉,苑克娥,时东锋,黄见,杨威,查林彬,朱文越

(1 中国科学院合肥物质科学研究院安徽光学精密机械研究所,中国科学院大气光学重点实验室,安徽 合肥 230031;

2 中国科学技术大学, 安徽 合肥 230026;

3 先进激光技术安徽省实验室, 安徽 合肥 230037;

4 脉冲功率激光技术国家重点实验室, 安徽 合肥, 230037)

0 引 言

湍流是一种极不规则且杂乱无章的宏观流体运动[1]。大气中温度分布不均的空气块随机运动会引起大气密度起伏,造成大气折射率的起伏,进而使光波在大气中传输时产生一系列光学湍流效应,包括闪烁[2]、到达角起伏[3]、光束扩展[4]和光束漂移[5]等。这些湍流效应为测量大气湍流强度提供了研究途径。衡量大气光学湍流强度最直接的物理量之一是折射率结构常数C2n,它是对折射率起伏强弱最直接描述的物理量。大气光学湍流随海拔高度的分布称为大气光学湍流廓线。相比于点式或整层大气光学湍流探测,大气光学湍流廓线的探测对激光大气传输和天文成像等具有更重要的价值和意义。

光线通过大气湍流产生的湍流效应,限制了多个领域的光电系统的应用。在成像或遥感等光学系统应用中,致使图像失真也使目标和背景的分辨率及对比度降低[6]。在激光工程、光通信系统和其他系统中,由于光学湍流效应的作用,激光光束相干性受到破坏,产生“光束漂移”。当光束偏离接收器时,信号会短暂地丢失[7,8],即通道漏码。传输在大气中的激光束还会受到湍流的衍射和折射的干扰,给光束造成空间和动态退化,不利于激光光束的长距离传输[9−11],降低了激光通信的性能[12−14]。对湍流强度进行准确测量,有助于理解自由光通信光波传播的信道效应[15]、光束相干度[16]、光强信号衰落[17]等,可用于评估通信链路的性能[18]。在温度遥感应用中,要求对辐射定量测量[19]。在存在湍流的情况下,辐射以不同的概率折射出并返回路径。通常利用光学湍流的强度廓线对其测量数据进行修正。无线电信号在大气传输中产生的延迟是全球导航卫星系统(GNSS)和测地甚长基线干涉测量(VLBI)等空间大地测量技术的重要误差源。利用大气折射率结构常数C2n对VLBI 测得的数据进行校正,可减少部分误差[20]。

大气湍流引起的一系列光学湍流效应,严重制约了激光技术的应用,限制了天文观测、大气光通讯、光学遥感等光电系统的性能发挥。了解和掌握大气折射率起伏即大气光学湍流的时空结构特征、实时测量湍流强度廓线对光传输研究和光电工程应用等具有非常重要的意义。多年来,国内外学者一直致力于大气湍流测量方法的研究,其测量方法主要分为温度脉动法和光传播方法。温度脉动方法是利用对大气温度起伏的测量间接得到大气湍流强度廓线分布,技术手段较为成熟。但由于大气光学湍流廓线在很大程度上是为光传输与光电工程提供应用,发展较为直接的光学测量方法可以避免间接测量带来的误差。光传播方法是直接对大气折射率的随机起伏导致的湍流效应(光波强度和相位起伏)进行测量,根据采用的光源不同,又可分为主动测量和被动测量两种方法。文中针对大气湍流强度廓线的探测方法,尽可能全面地分析、对比和总结了温度脉动法和光传播方法探测技术的进展及存在的优缺点,并展望了大气湍流激光雷达探测发展趋势,介绍了实验室研制的用于大气光学湍流廓线探测的差分波前激光雷达系统。

1 温度脉动法

温度的随机起伏是湍流的特征,早期获取大气折射率结构常数通常利用该特征[1]。温度结构函数是描述相距ρ=|ρ|的两点温度起伏的统计量之一,表示为

式中: r 是单点位置,T 是温度(K),〈···〉是集合平均。在Kolmogorov 的局部均匀各向同性湍流理论下,惯性子区之外,结构函数趋向于一个常数;惯性子区内(l0＜ρ ＜L0),温度的结构常数为

利用Gladstone 定律可得出折射率结构常数,其关系式[21]为

式中: 常数c 值取决于具体的环境,P 是气压(hPa)。

目前,根据上述原理反演得到大气湍流廓线的技术有微温传感器、Sodar、微波辐射和声速仪。若利用该类方法的测量结果对光传输研究和光电工程提供应用,会存在一定的误差。

1.1 微温传感器

Bufton 等[22]最早于1972 年详细地介绍了利用搭载在探空气球上的一对微温传感器来获得大气湍流廓线的方法,该方法是根据微温传感器测量路径上的温度脉动,在已知大气压力P 和温度T 的情况下,通过式(3)获得路径上的大气湍流强度廓线(h)的工作。相关人员之后还开展过将微温传感器搭载在飞艇[23,24]和桅杆上[25]来获得大气光学湍流廓线的研究。由于该探测方法原理简单并且测得的数据空间分辨率高,得以广泛应用,但实时性差。近年来,Wu 等[26]利用探空气球在拉萨首次进行了大气光学湍流廓线探测,每条20 km 廓线需要两个小时。

1.2 Sodar

1981 年Moulsley 等[27]详细阐述了Sodar 测量技术和理论,得出了温度结构常数。之后Forbes 等[28]利用发射声波来测量温度结构常数,进而获得折射率结构常数。由于需要测量不同高度上的大气光学湍流强度,所以该设备安装在铰链装置上[28]。的计算公式为

式中: PR为实测功率;T0为局地平均温度(K);exp(2R¯α)是由空气衰减引起的往返损失功率, ¯α 是在R(m)范围内散射体引起的平均衰减(m−1); Le为由额外的衰减和风速影响的有效效率;ER为接收声功率转换效率;PTET是辐射功率,PT为施加转换器的电能,ET为转换为声辐射功率的效率;c 是声速(ms−1);τ 为脉冲长度(s−1);κ 为入射声波数;AG/R2是散射体在R(m)处的天线孔径A(m2)对应的立体角,由天线方向引起的有效孔径因数G 修正。根据式(4)计算出,再利用式(3)得到。

Sodar 只能探测边界层内较低的高度,约为300 m 以下[28,29]。Sodar 具有可运输性,系统成本相对较低。但声波衰减较大,探测范围有限且探测信号很容易受到来自外部噪声源的污染[30],近年来用其测量湍流廓线的相关研究较少。

1.3 声速仪

声速仪(Sonic anemometers)是根据超声波传感器来测得风速及温度。由于微温传感器[31]在刮风和结冰的情况下易损坏,Aristidi 等[21]利用三对超声波传感器组成的声速仪探测南极Dome C 站点的湍流廓线。在铁塔8、17、24、31、39、45 m 处分别放置该声速仪,测量三个正交轴(即U、V 和W,其中W 为垂直轴)的风速以及温度T。由于是单点测量,故在Taylor 假设基础上,利用由各个高度上的单点温度起伏推出温度结构函数,即

式中: ν 为风速,∆t 两次测量时间间隔。再利用式(2)、(3)得到湍流廓线。为了获取有统计意义的数据,需要对其进行时间平均。经过一系列的实验得出30 分钟是一个合适的时段。

此外,还有一种方法来计算温度结构常数,即

1.4 微波辐射

微波辐射法(Microwave radiometric method)在Taylor 假设的基础上,通过微波辐射测量出,进而得到大气折射率结构常数[32]。的计算关系式为

式中: 〈···〉是集合平均,KC是交越频率, ¯U 是水平平均风速,ν 是随机起伏分量,∆t ≫1。之后再结合式(3)即可得到折射率结构常数。该方法反演得到的高空大气湍流强度数值偏大一个量级[32],这主要归因于交越频率是敏感参数,较难准确测量。为了避免这种情况,Vyhnalek[33]在辐射计温度测量的基础上利用几何射线追踪和延时成像技术的计算方法来获取大气折射率结构常数。

2 光传播法

光学湍流效应实际上都是随机介质对光波振幅和相位的影响。光传播法就是利用光波振幅和相位的变化来反演大气湍流强度的技术。该方法除了观测量和研究方法直接相关外,还有时间和空间的优越性。根据采用的光源不同,将其分为主动测量和被动测量两大类。

2.1 被动测量方法

2.1.1 SCIDAR

SCIDAR(SCIntillation Detection and Ranging)是Vernin 和Roddier 在1973 年为了测量光学湍流廓线而提出的概念[34],其主要思想是: 对穿过大气的双星光线进行快速记录,将获得的闪烁图像进行自相关和互相关处理,反演出h 高度的湍流强度,即折射率结构常数(h)。图1 为其原理示意图。

夹角很小的两颗星体光源在高度h 处同时受到湍流层的扰动,对应到望远镜焦面上是两点的光强度起伏特性。望远镜所观测到的闪烁星像,包含了该层湍流的信息。通过两个像差的相关运算,可以对湍流层的高度进行三角测量,相关峰值的幅值对应于该层的湍流强度。h 高度的湍流层产生的闪烁自相关函数由三个部分组成,一个在原点中心,另外两个在θh 和−θh,θ 为双星分离角[35]。闪烁自相关函数与的关系式为

式中: C(r,h) 是h 高度的恒星闪烁自相关函数, h 为湍流层高度, r 是自相关函数中心峰值的位置, 因子a=(1+α2)/(1+α)2, b=α/(1+α)2,α=10−0.4∆m,∆m 为双星星等差。

图1 SCIDAR 原理图Fig.1 Principle diagram of SCIDAR

SCIDAR 要求望远镜主镜直径大于1 m,庞大的体积导致这种仪器难以选址[36]。其测量所需的双星需在一定的角度范围内,不适合持续观测[37];且双星星等小于5～6 等星,从而减少了可供使用的恒星数目。该方法可以测量25 km 以下的大气湍流廓线,高度分辨率约几百米,但其对近地面湍流并不敏感。Fuchs[38]等随后提出了Generalized SCIDAR 方法来克服该缺点, 可以测量从望远镜至大气顶的完整大气湍流路径。Shepherd 等[39]在此基础上于2013 年提出具有高灵敏度的stereo-SCIDAR 技术,采用两个CCD 对两个星体分别成像。随后,Osborn 等[40]将stereo-SCIDAR 测量数据与SLODAR 和MASS 数据进行了对比,结果表明具有一定的相关性,但仍需继续验证其数据可靠性。

2.1.2 SLODAR

Shack-Hartmann 传感器主要由微透镜阵列和面阵CCD 探测器构成,微透镜阵列对光波畸变波前采样,光束聚焦成一个光斑投射到对应到CCD 阵列上。因波前倾斜聚焦光斑相对于CCD 定标中心会有随机漂移,测量光斑中心在水平和垂直方向的漂移量,就可以求出各子孔径范围内的波前在两个方向上的平均斜率,最终可以求得相位的起伏方差。相位起伏方差与湍流折射率结构常数之间的关系[19]为:

式中: dsub是望远镜瞳孔的子孔直径,γ 为观测的天顶角。

SLODAR 系统的垂直分辨率∆h 满足关系式

式中: dtelescope是望远镜瞳孔直径,n 是望远镜横向瞳孔的子孔数,θ 是双星之间的角度。该技术可以通过增加瞳孔的子孔数或双星之间的角度来提高分辨率。尽管该方法的高度分辨率受到Shack-Hartmann 传感器空间采样限制,但相比于SCIDAR,它的硬件成本较低[41]。

图2 SLODAR 原理图Fig.2 Principle diagram of SLODAR

图3 Paranal 天文台的SL-SLODAR 系统图(a)和原理图(b)Fig.3 Photograph(a)and principle diagram(b)of SL-SLODAR system at Paranal observatory

Wilson[41]早期利用SLODAR 测量的数据分析表明,近地面包含了整个大气层高度湍流强度的一大部分。然而SLODAR 无法准确地测量该范围的湍流强度。为了实现近地面高分辨率观测, Osborn 等[43]提出了SL-SLODAR, 用以测量近地面近百米的大气光学湍流廓线。图3 简单地展示了Paranal 天文台的SL-SLODAR 技术方案[44]。该方案中利用反射楔将两颗目标恒星的光分离到独立探测器的波前传感器中。使用光学三角测量方法在地面观测分隔双星(＞100′′)两条不同路径的波前相位差斜率的空间协方差,用来确定湍流廓线。SL-SLODAR 给出了从望远镜瞳孔开始的8 层(∆h)6～16 m 之间分辨率的(h),其分辨率取决于双星分隔θ 及其天顶距。

2.1.3 MASS

系统的基础设备在不同网络架构下的运行方式。其主要运行模式有：分布式电源/微电网联合并网运行、分布式电源/微电网联合离网运行、微电网独立并网运行等。在不同的运行模式下，其对分布式电源、负荷及储能的控制策略和能量分配策略也不一样。

Kornilov 等[45]于2003 年首次提出利用MASS(Multi-Aperture Scintillation Sensor)技术。它通过四个同心光阑探测单颗星体产生的闪烁空间特性, 计算四个常规闪烁指数和六个差分闪烁指数来反演湍流廓线[45]。其原理见图4。

图4 MASS 原理图Fig.4 Principle diagram of MASS

在弱起伏的情况下,大气湍流闪烁指数s2与折射率结构常数关系[45]为

式中: W(z)为权重函数,z=hsecγ,h 为高度,γ 为天顶角。在已知权重函数下,反演出高度0.5、1、2、4、8、16 km 的六个薄湍流层上的湍流强度。其分辨率满足∆h/h ～0.5。随后,Els 等[46]为MASS 仪器测量精度进行了评估,表明MASS 测量结果可靠,对轻微的配置差异相对不敏感。该技术设计成本低,设备安装简单。由于以单星为光源,探测方便,能够进行连续观测。但其在垂直方向的空间分辨率较低,仅能获得七层的湍流强度[29]。通常与DIMM 联合来获得1 km 以下的湍流强度。原则上,如果MASS 的孔径与望远镜瞳孔的散焦图像共轭,就可以测量近地面湍流廓线[36],与G-SCIDAR 原理相似。

2.1.4 LuSci 和MooSci

Hickson 等[47]最早利用月亮来测量夜间近地面湍流强度。LuSci(Lunar Scintillometer)和MASS 相似,它通过测量来自月亮光线的归一化闪烁协方差,来估计近地面不同高度上的湍流强度[19]。采用六个线性结构的光电二极管(PD)对月光的快速起伏量进行测量,并在计算机上进行数字化和记录。其原理见图5[48]。

每对信号之间的协方差计算式为

式中: ζi= Ii/〈Ii〉−1 是在i 探测器处光电流Ii的归一化起伏量, K 是累积时间内收集的信号样本数。Tokovinin 等[48]选取的累计时间段为1 min,其中每2 ms 记录一次信号的起伏量。信号的协方差与湍流强度廓线的关系式为

式中: z 轴的方向是由仪器指向到月亮,x,y 为垂直z 轴平面内的坐标, W(x,y,z)为权重函数。

图5 LuSci 原理图Fig.5 Principle diagram of LuSci

LuSci 是一个稳健且廉价的方法,可用于探测500 m 以下的光学湍流廓线[49]。由于该仪器要求月球照度大于80%,所以LuSci 只能在满月前后使用10 天,不适合近地层持续观测。

Thomas-osip 等[49]在LuSci 的基础上,通过将LuSci 的圆形探测器改为5.8 mm 的正方形,并在两个相同的基线上均放置探测器等改进,发展了MooSci。实际上MooSci 等同于将两个LuSci 仪器沿着同一轴线放置,两者的测量结果有较好的一致性。

2.2 主动测量方法

2.2.1 DIM

Eaton 等[50]为DIM(Differential image motion)技术提供了早期的理论基础,Belen′kii 等[51]于2000 年对DIM 激光雷达探测概念进行了实验验证。DIM 激光雷达是将DIMM[52](Differential image motion monitor)中的星体光源用激光代替,采用脉冲激光和距离选通成像系统测量湍流廓线[51]。其原理是用双孔望远镜接收聚焦在选定测量高度上的激光后向散射光,之后用玻璃楔将散射在焦平面的两幅图像分开,通过计算差分像运动的方差来反演湍流廓线。

为了简化噪声模型,采用开窗法计算焦平面质心的位置,即仅考虑距图像中心一定半径范围内的像素点,该方法通常将最亮的像素坐标作为已知的中心[53]。大气湍流廓线与DIM 雷达探测的质心方差之间的关系[54]为

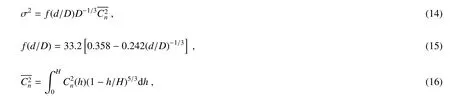
式中: d 为望远镜两个子孔间距(m),D 为望远镜子孔的直径(m)。联立式(14)、(15)、(16)即可反演出大气湍流廓线(h)。

DIM 方法具有对湍流外尺度变化不敏感、不会产生饱和现象、测量结果不受激光稳定性影响等优点[54]。近年来,DIM 雷达系统不断发展[55,56],但仍存在一些缺点,其采用聚焦在特定高度上的光源作为激光导星,存在聚焦焦移问题,且探测的空间分辨率较低,故不利于大气湍流廓线的高分辨率准确测量。

2.2.2 DCIM

Jing 等[57]于2013 年在DIM 雷达的基础上发展了DCIM(Differential column image motion)激光雷达,该装置用倾斜焦平面对一定高度范围的激光光柱成像,通过处理光柱图像可以得到不同高度的大气相干长度r0,进而利用合适的反演算法得到湍流廓线,测量高度范围为0～15 km。该方法克服了DIM 雷达分时测量r0受地面扰动的缺点。程知等[58]详细地介绍了该雷达系统,并对其探测数据进行了降噪及误差分析。DCIM采用旁轴结构,激光光束通过小口径发射系统发射至大气中,含有大气湍流信息的激光回波信号通过望远镜的两个子孔,成像在CCD 的焦平面上,获得两条散射光柱图像,其原理见图6。

图6 DCIM 雷达系统原理图Fig.6 Principle diagram of DCIM lidar system

大气相干长度r0与经向差分图像方差关系为

r0与的直接关系式为

式中: r0为Fried 横向相干长度, k 为波数, H 为传播距离。基于式(18), 通过测量不同高度上的r0(H1)、r0(H2)、r0(H3)等可得到大气湍流强度廓线。

该方法每22.5 s 可测得一条0～15 km 的湍流廓线,时间分辨率较高。但由于算法的限制,反演出的湍流廓线没有确定的空间分辨率,并且在近地面具有较大的误差。

2.2.3 Cross-Path

Belen′kii 等[59]于2007 年提出Cross-Path 雷达技术,采用人造双星测量大气湍流廓线。其原理类似于双星的SLODAR 方法,但是它采用激光生成两个激光导星来代替双星,克服了SLODAR 不易找到合适双星位置的限制。其原理见图7。同时雷达本身能够在移动平台上测量。激光脉冲在固定的测量范围内产生间隔为θ 角度的两颗激光导星,Hartmann 波前传感器和门控相机测得双激光导星穿过大气湍流层的波前倾斜。测量系统所用的Hartmann 子孔个数为nsub=dtelescope/dsub,其中dtelescope为望远镜孔径直径,dsub为子孔直径。波前斜率的互相关函数在双星分离方向S 基线上有一个峰值,该峰值与H 高度上的湍流强度有关。

波前斜率的互相关函数可用相位结构函数表示为

对于垂直传输方向上的Kolmogorov 湍流模型有

式中: L 为激光导星与接收望远镜的距离,ρl= ri+dsub。对于自然导星L = ∞。对于激光导星,假设ri和dsub与θ 向量平行。则波前斜率与湍流廓线的关系式为

式中: b(ri,θ)是归一化的斜率互相关函数, b(ri,θ) = 〈dsub1dsub2〉/〈d〉, W(ri,θ,z)是权重函数。根据式(19)、(20)、(21)可得到湍流廓线。

Cross-Path 雷达具有时间分辨率高、不产生饱和现象等优点。但其空间分辨率取决于Hartmann 波前传感器的子孔数,且其测得的廓线并不是完全垂直的,近年相关研究较少。

2.2.4 光强闪烁激光雷达

1994 年Belen′kii[60]提出了根据残余闪烁效应,利用激光光束的后向散射光强起伏来反演大气湍流强度的技术的理论基础。随后,又讨论了系统设备选取的注意事项[61]。2013 年崔朝龙等[62]研制出了一台光强闪烁激光雷达,并在水平方向上开展了探测实验。在此基础上,2018 年赵琦等[63]使用EMD 降噪后的回波信号获取不同高度上闪烁指数变化,利用分层迭代算法得到了有限内尺度和不考虑内尺度条件下的湍流廓线。该类雷达系统原理结构图见图8。

图8 光强闪烁激光雷达原理结构图Fig.8 Principle diagram of scintillation lidar system

式中: k 是波数,L 是探测光束传播的距离,Q1=10.89L/k,a1=1/Q1,b1=z(1 −z/L),Q1=tan−1(b1/a1),Γ(a)为Gamma 函数。根据式(22)-(25)即可得出C2n廓线。

该技术与DIM 雷达相比,具有测量对象直观、技术难度较低、空间分辨率较高等优点。但设备探测高度范围小(0～2 km),且准确度受到激光稳定性、设备振动等影响。

3 激光雷达的未来发展趋势

当激光在大气介质中传播时,激光雷达的后向散射信号受到大气湍流的影响,通过距离选通的方式接受不同高度的后向散射信号可测得大气光学湍流廓线的分布。激光雷达是一种非常成熟的主动式遥感探测技术,具有时间分辨率高、方向性好、测量精度高等优点,适用于大气的探测和研究[64]。未来为实现大气光学湍流廓线的精准测量,激光雷达探测将成为主流。

针对前述探测技术的优缺点,在前人研究的基础上,实验室拟开展基于差分波前激光雷达系统探测大气湍流廓线分布的技术方法研究。系统结构如图9 所示,基本原理为:激光光源经扩束后准直发射到大气中,利用望远镜双孔接收雷达回波信号,利用具有单光子探测能力的ICCD 对信号进行探测,分析波前的差分抖动,实现大气湍流廓线的高分辨探测。该系统激光光源准直发射,不会存在类似DIM 雷达的聚焦焦移带来的探测误差,具有较高的测量精度,同时,ICCD 纳秒级的距离选通功能使得高度分辨率可达米量级。从而实现大气光学湍流廓线高精度高度分辨率的时空分布探测。

根据激光雷达大气回波方程,可得通过望远镜每个子孔的光束在ICCD 光斑成像时,系统接收的光电子数为

图9 差分波前雷达系统原理图Fig.9 Principle diagram of differential wavefront lidar

图10 望远镜单孔接收光电子数随高度的变化及高度分辨率的变化(a)和不同高度分辨率下光电子数随高度的变化(b)Fig.10 Variation of photoelectron number received by single aperture of telescope with height and resolution(a)and variation of photoelectron number with height under different height resolution

式中: A 为望远镜子孔面积;Q0= E0/hcv为激光脉冲发射的光电子数, E0为脉冲激光总能量,h 为普朗克常数,v 为激光发射频率(用波数表示);χ 为激光雷达接收系统的光学透过率;kq为ICCD 光量子效率;β(R)为距离R(m)处大气介质的体后向散射微分截面;T 为激光脉宽;S(R)为距离R 的激光光束截面积;ds 为距离R 处激光雷达发射光束与接收视场角相交截面上面积元;σ(r)为大气消光系数,r 为垂直方向的距离变量。大气对532 nm 的后向散射和消光系数采用美国标准大气532 nm 分子和气溶胶模式。图10 表示了不同高度分辨率∆r 下,望远镜单孔回波光电子数在不同高度下的对数分布,其横坐标为高度分辨率,纵坐标为海拔高度,填色值为回波光电子的对数lgQICCD。在高度分辨率为20、40、60 m 时,10 km 高度上回波光电子数可达到102～103;在高度分辨率为80、100 m 时,10 km 高度上回波光电子数可达到103～104。结果表明,差分波前激光雷达能对湍流廓线进行有效的探测。

本系统尚属研制初级阶段,测量结果的可靠性和误差分析等还需要通过大量的实验来验证,以期成为大气湍流廓线高精度高度分辨率的常规观测设备。

4 结 论

目前,大气光学湍流廓线的探测方法主要有温度脉动法和光传播法。温度脉动法属于间接测量,存在一定的误差,所以发展较为直接的光学测量方法非常必要。而在已发展的多种光学方法中,被动测量方法存在一个共同局限性,就是以恒星作为光源,容易受到测量方向、测量时段和测量场景等影响。相关人员可以根据探测条件和目的选取恰当的探测手段,若限于探测成本,可选温度脉动法,将微温传感器搭载在气球上;若在陡峭的山上探测,受制于其地理条件可选取系统体积较小的被动探测法;如为了实时探测,可选取激光雷达主动探测。激光以其高相干度、高亮度、方向性好等优点代替了自然导星,激光雷达探测大气湍流得以发展。针对已发展的激光雷达存在聚焦焦移、探测高度分辨率低等问题,提出了差分波前激光雷达系统探测大气光学湍流廓线的方法。通过回波仿真,表明该雷达能对湍流廓线进行有效探测。后续工作会评估该系统探测数据。