浅析用于变换器的高阶并网滤波器
王江涛 陈国栋 叶傅华
浅析用于变换器的高阶并网滤波器
王江涛 陈国栋 叶傅华
(上海电气输配电集团技术中心,上海 200042)
本文首先分析了LCL型并网滤波器,给出了相应的参数设计步骤,并通过Matlab仿真得到网侧电感与机侧电感比值对滤波电容容值选取的影响,以及该比值对纹波电流分流的影响,同时分析了有源阻尼策略在LCL型滤波器中的应用;然后,又在LCL基础上对分裂电容型高阶滤波器做了详细分析,得到两个分裂电容比例对整体滤波性能的影响,同时提供了应用该类型滤波器的无功补偿器试验波形;最后,在分裂电容型高阶滤波器基础上增加LC陷波器支路,并分析得到阻尼电阻对滤波器整体性能的影响,同时提供了应用该类型滤波器的无功补偿器试验波形。
LCL型滤波器;分裂电容型高阶滤波器;有源阻尼
0 引言
随着电力电子装置的广泛使用,因其所产生的电能质量问题变得愈来愈严重,并网滤波器作为变换器与电网之间的接口,其拓扑结构与参数设计的合理与否直接影响到变换器的性能与电力电子装置对电网的负面影响程度。
并网变换器接入电网示意图如图1所示。

图1 并网变换器示意图
本文首先分析了LCL型高阶滤波器,给出了相应的参数设计步骤,常规设计中关于滤波电容的选取是基于注入到系统的无功功率限值[1-2],未考虑到滤波器中电感与电容之间的依赖关系。文献[3]给出了无源阻尼型LCL滤波器的参数设计步骤,其中滤波电容参数设计是基于基准阻抗给出的经验值。文献[4]提出了一种基于谐振频率的LCL参数设计方法,重点关注在弱电网条件下的系统稳定性和鲁棒性。文献[5]通过分析分裂电容电流反馈控制的原理及谐振特性,基于增大系统带宽的角度考虑,采用分裂电容电流反馈可使被控系统由三阶系统转换为一阶系统。本文建立各种类型滤波器数学模型,并推导出相应的数学公式,重在剖析参数间相互依赖关系,如通过公式推导分析得到网侧电感与机侧电感比值对滤波电容容值选取的影响,以及该比值对纹波电流分流的影响,为滤波器设计提供理论依据。首先分析基于有源阻尼策略的LCL型滤波器,并通过采用受控源的形式推导出各参数与滤波器整体性能的函数关系。然后,在LCL基础上对分裂电容型高阶滤波器做详细分析,得到两个分裂电容比例对整体滤波性能的影响,同时提供应用该类型滤波器的无功补偿器试验波形。最后,在分裂电容型高阶滤波器基础上增加LC陷波器支路,并分析得到阻尼电阻对滤波器整体性能的影响,同时提供应用该类型滤波器的无功补偿器试验波形。
1 LCL型高阶滤波器
1.1 传递函数推导及参数设计
LCL型滤波器等效电路模型如图2所示。式(1)为网侧电感电流与变换器输出电压之间的传递 函数。
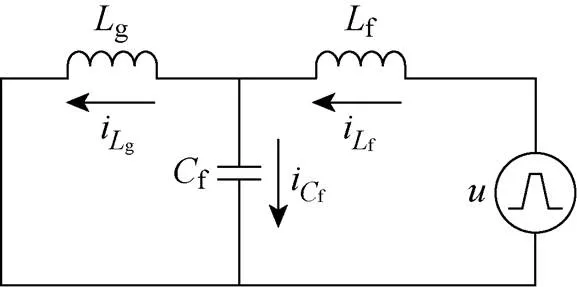
图2 LCL滤波器等效电路模型

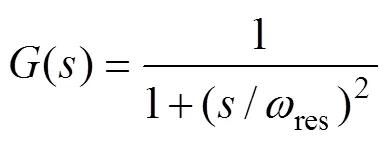
由式(1)可以看出,该传递函数可以分为两个环节,积分环节(电感)与二阶无阻尼振荡环节,通过调整谐振频率,可以改变开关纹波的衰减率,谐振频率越低,对高频纹波衰减程度越强,但同时会影响系统的低频特性。设计LCL型滤波器时,可以按照单电感滤波器设计方法,确定电感的取值范围(上限由变换器最大输出能力所决定,下限由纹波电流允许值所决定)。一般情况下,单电感滤波器较难满足纹波电流允许值的技术要求,或者即使满足,考虑到体积和成本,通常会选取较小的电感参数。
待总的电感值确定之后,可以根据该值与谐振频率设定值确定滤波电容及网侧、变换器侧电感比值的取值范围。其推导过程为
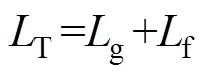


图3为滤波电容容值随k值变化曲线图,其中LT=520mH,fres =4kHz,工程设计时,基于成本与体积的考虑,一般选取容值相对较小的电容,k值宜选取在曲线谷点附近。
1.2 有源阻尼策略在LCL型滤波器中的应用
式(2)中,()为二阶无阻尼振荡函数,属于不稳定环节,其伯德图如图4所示。
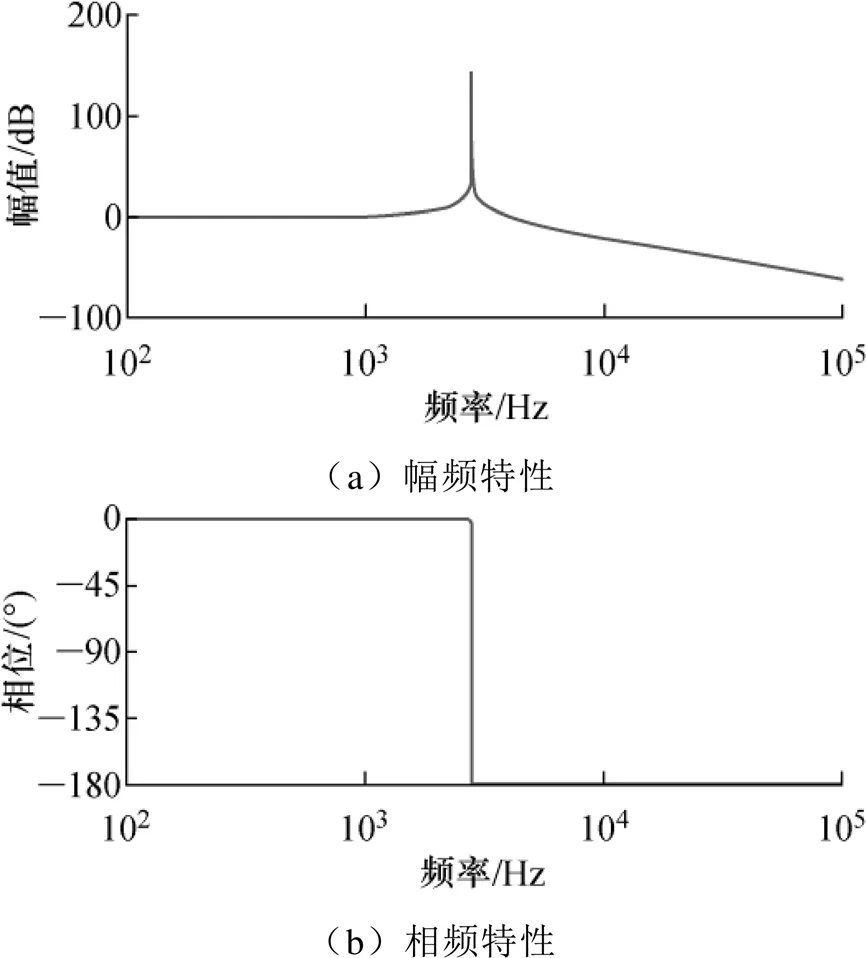
图4 G(s)函数伯德图
由图4可以看到,其幅频特性曲线中存在一个较大的谐振峰。为了抑制该谐振,可以将有源阻尼策略应用于LCL型滤波器,等效为在滤波器中增加了一个电流受控源,等效的电路如图5所示。

图5 采用有源阻尼策略的LCL滤波器等效电路图
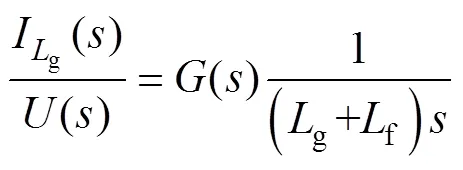


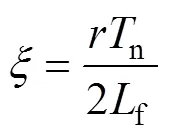
从式(7)可以看出,加入有源阻尼策略后,等效为在G(s)函数分母中增加了一次项,由式(9)可知,通过调整有源阻尼系数r来改变系统的阻尼比。图6为加入有源阻尼策略后G(s)函数的伯德图(Lg=120mH,Lf=400mH,Cf=18mF,r=1),从图中可以看到,谐振峰被大大削减。
图7为动态无功补偿装置的试验波形,该试验装置采用的是LCL型并网滤波器(参数同仿真),并使用有源阻尼策略。图中,三相网侧电感电流方均根值约为52A,中线电流方均根值为1.47A。

图7 采用有源阻尼策略试验波形图
2 分裂电容型高阶滤波器
第1节介绍的LCL型滤波器,为了抑制其固有的谐振,采用了有源阻尼策略。工程上,也有采用无源阻尼来抑制谐振,一般通过在滤波电容支路上并联或串联电阻来实现。以串联电阻为例,一方面电阻会产生额外的损耗,降低系统效率;另一方面,对高频纹波的抑制强度将会减弱。鉴于此,可以考虑将电容支路分成两条,其中一条支路上串联电阻,电路如图8所示。

图8 分裂电容型高阶滤波器电路模型
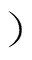
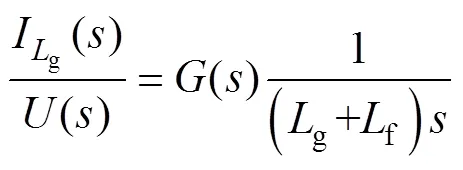
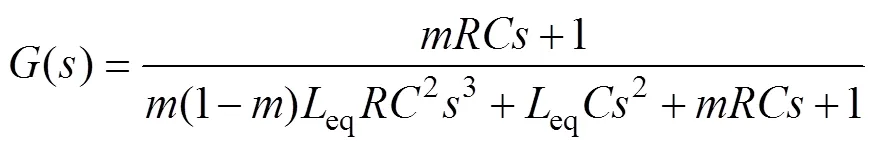

因惯性元件的增加,该滤波器阶数增高,通过Matlab编程计算可以直观了解传递函数的特性。图9为式(11)中()函数幅频特性随值变化的三维图(g=120mH,f=400mH,=16mF,=5W)。从图中可以看出,值宜取在0.5附近。
图10为动态无功补偿装置的试验波形,该试验装置采用的是分裂电容型高阶滤波器(参数同仿真),图中,网侧电感电流方均根值为51.72A,流经无源阻尼电阻的电流方均根值为2.486A,无源阻尼电阻两端的电压方均根值为12.12V。
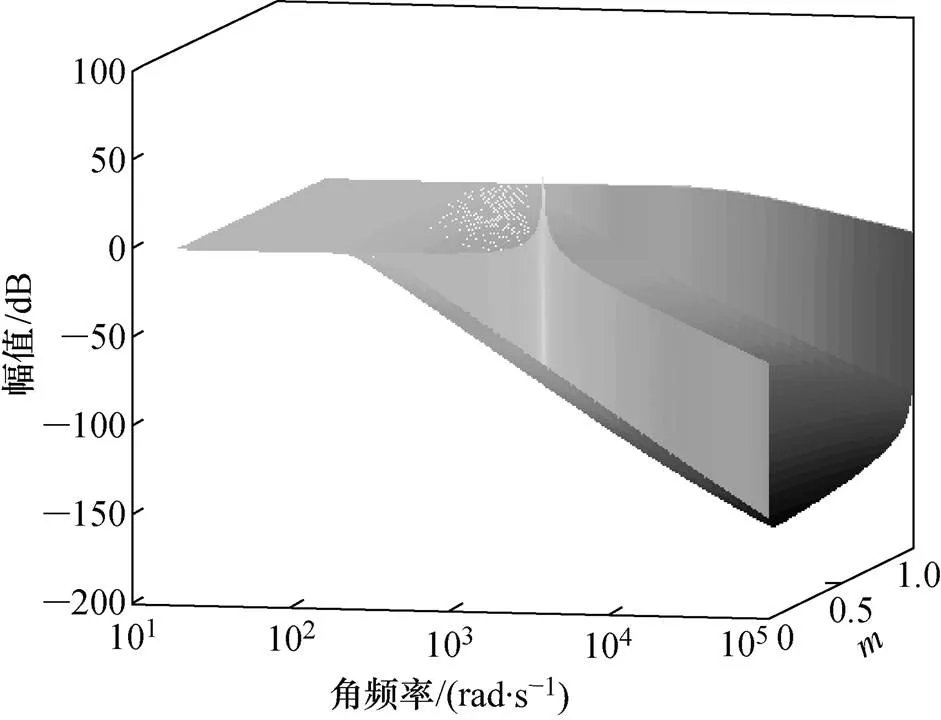
图9 G(s)幅频特性随m值变化三维图
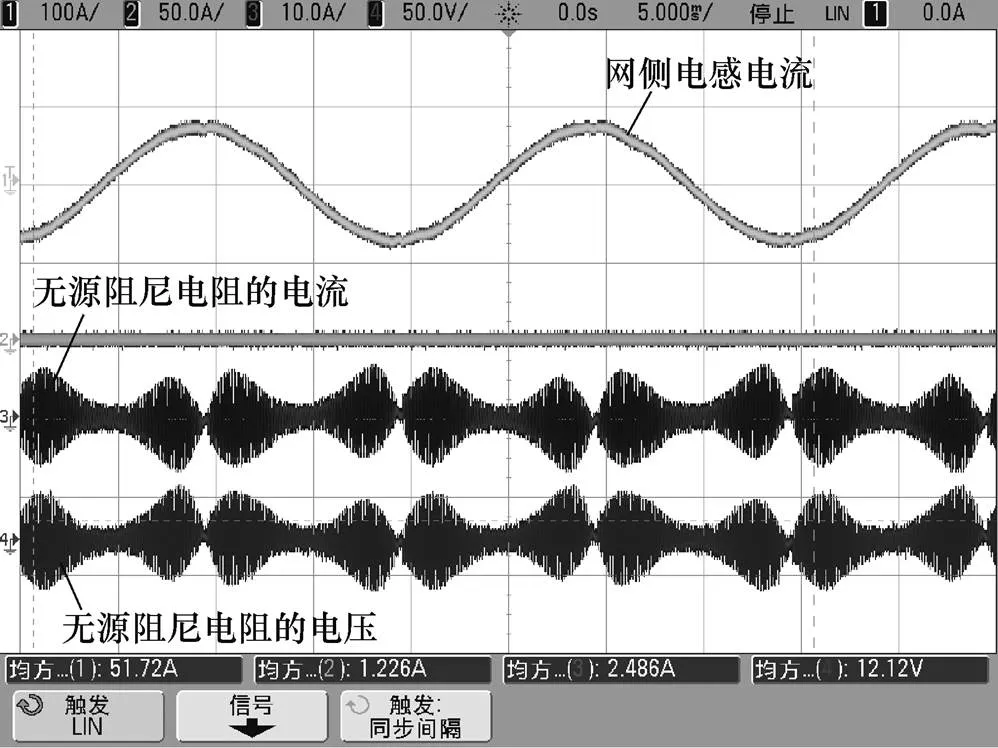
图10 分裂电容型高阶滤波器试验验证图
3 带陷波器支路的高阶滤波器
为了进一步减小流过电阻的电流,可以在分裂型高阶滤波器支路上,额外增加陷波器支路,中心频率为变换器的开关频率,该类型滤波器等效电路如图11所示。

图11 带LC型陷波器支路的高阶滤波器电路模型
该电路的传递函数推导如下。
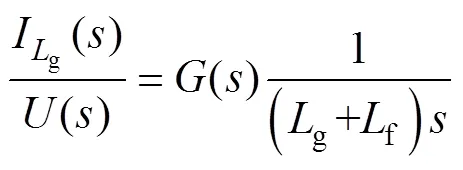
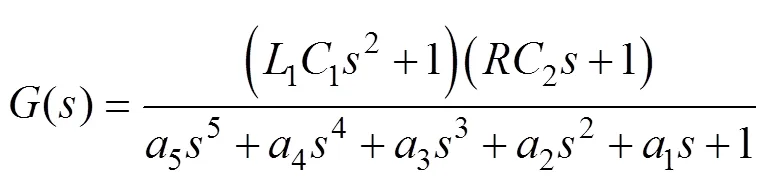

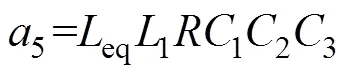
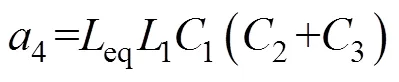



利用Matlab计算绘图可以对式(14)中()函数进行特性分析,图12为()函数幅频特性随电阻值变化的三维图(g=120mH,f=400mH,1= 33mH,1=4.7mF,2=3=8mF)。从图中可以看出,幅频图上有两个谐振峰,从轴看过去,存在值使得两个谐振峰最小。

图12 G(s)幅频特性随R值变化三维图
图13为动态无功补偿装置的试验波形,该试验装置采用的是带陷波器支路的高阶滤波器(=5W,其他参数同仿真)。图中,网侧电感电流方均根值为51.39A,流经LC支路的电流方均根值为7.894A,流经无源阻尼电阻的电流方均根值为0.799A,无源阻尼电阻两端的电压方均根值为3.34V。此试验与图10的试验相比,滤波器参数唯一不同之处在于增加了LC陷波器支路,对比图10与图13,流经电阻的电流有效值由图10的2.486A减小为图13的0.799A,绝大部分开关纹波电流都从LC支路流通,大大降低了额外的有功损耗,同时可以选用较小功率的电阻。
以上章节对3种类型高阶滤波器进行了详细分析,表1从设计难度、滤波效果、成本、稳定性、效率等几个方面对这几种高阶滤波器进行了优劣对比。

图13 带陷波器支路的高阶滤波器试验验证图

表1 3种高阶滤波器优缺点对比
4 结论
本文依次分析了LCL型高阶滤波器、分裂电容型高阶滤波器以及带陷波器支路的高阶滤波器,并通过Matlab分析了各滤波器的幅频特性,给出了设计参数间的依赖关系,通过图形方式可以很直观地确定参数的选取范围,上述3种高阶滤波器都通过实际试验得到了验证,最后对比了3种滤波器的优缺点,为高阶滤波器的工程设计提供参考。
[1] 张宪平, 李亚西, 潘磊, 等. 三相电压型整流器的LCL型滤波器分析与设计[J]. 电气应用, 2007, 26(5): 65-68.
[2] 刘超, 赵争鸣, 鲁挺. 三电平PWM整流器网侧LCL滤波器设计, 电工电能新技术[J]. 2012, 31(1): 56-59.
[3] 周圆, 任一彪. 用于光伏并网逆变器LCL滤波器的优化设计[J]. 电工技术, 2018, 11(22): 34-37.
[4] 刘芳, 张喆, 马铭遥, 等. 弱电网条件下基于稳定域和谐波交互的并网逆变器LCL参数设计[J]. 中国电机工程学报, 2019, 39(14): 4231-4241.
[5] 赵清林, 许方玲, 杨秋霞, 等. 基于LCL滤波器并网逆变器分裂电容控制研究[J]. 太阳能学报, 2016, 37(4): 815-822.
Analysis of the high-order grid-connected filter for the gird-connected converter
WANG Jiangtao CHEN Guodong YE Fuhua
(Shanghai Electric Power T&D Group Technology Center, Shanghai 200042)
This paper analyses the LCL-type grid-connected filter firstly. It gives proper designing steps. Through Matlab simulation, we get the affection of the ratio of the grid side inductor and the converter side inductor to the filter capacitor value and the cripple current. Simultaneously it analyses the application of the active damping control strategy into the LCL-type grid-connected filter. Then it analyses the splitting capacitor-type high order filter in detail. We get the affection of the splitting capacitor values to the filter performances, and the experimental waveforms using this type high-order filter into the static var generator. Finally basing on the splitting capacitor-type high order filter, it adds a LC trap branch, and analyses the affection of the damping resistor to the filter performances. We also get the experimental waveform using this type high-order filter into the static var generator.
LCL-type grid-connected filter; splitting capacitor-type high order filter; active damping
2020-05-06
2020-07-03
王江涛(1982—),男,硕士,主要从事电能质量方面的产品研发与应用工作。

