数值模拟河道疏浚后的泥沙再平衡过程研究

王 蒙，贺 苗，杨 慧，李栋梁

(徐州市水利建筑设计研究院，江苏 徐州 221000)

1 试验背景

河流集料被用作各种行业的原料，但是收集这些集料会影响河流中土石料的平衡，从而导致土石料的缺乏[1-3]。它会引起河底、底部宽度和床底的变化，从而导致河床冲蚀、侵蚀，并导致河流侵蚀和河流横向不稳定，以及码头冲刷和维修结构的稳定性问题。它降低了地下水位并影响了生态系统的栖息地[4-6]，因此，系统地调查和了解河流土石料的采集和疏浚影响下河流的适应过程，对于规划或管理受洪水影响显著的河流非常重要[7-10]。本试验以江苏省徐州市湖西地区疏浚工程实施为契机，利用当地河沙完成试验，为工程开展提供一定的技术支持。

评估河流中土石料采集(或疏浚)的各种影响，重要的是要了解水流，上游水流携带的土石料会和复杂的河道地形相互作用。Wu和Wang(2008)[11]则提出了对于土石料采集(或疏浚)河流工程的设计和管理方法：一维数值模型，建议使用最大深度和最大长度的头部侵蚀和尾切的经验包络法。但是这个方法存在一个局限性，即该模型的适用性尚未得到审查。为了研究河道底部采集点(疏浚点)，分析了藻类在河道土石料采集点(疏浚点)的浓度变化，并使用二维河床波动数值模型根据流向和河流剖面的变化确定了沉积过程。

先前开发的数值模型在定量识别土石料采集而引起的河流平面区域变化过程中存在局限性[12]。因此，本研究体现了总坐标系中的水流和床面波动在河流平面视图上的变化。利用能够模拟河床的二维数值模型，定量确定了根据河床坡度变化和采集(疏浚)规模引起的河床响应特征[13-15]。

2 控制方程介绍

在本试验的数值模型中，利用与由笛卡尔坐标系转换为总坐标系的二维千位数方程相似的连续方程式来计算床层相位波动，该流动方程式的连续方程式和动量方程式如下：

连续方程

(1)

动量方程

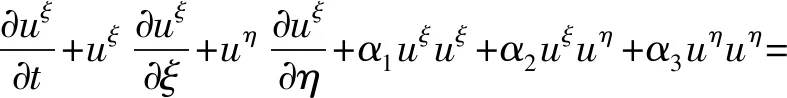
(2a)

(2b)

(3a)

(3b)

式(2)中的动量方程的扩散项Dξ和Dη可以表示为

(4a)

(4b)

在一般坐标系中，二维连续多态方程如下：

(5)

为了计算贯流进给速度，考虑了离心力引起的二次流和侧向斜率，ξ和η方向的流量计算如下：

(6)

(7)

(8)

式中，V—深度平均流速。

根据Engelund(1974)的假设，β可以表示如下：

β=3(1-σ)(3-σ)

(9)

在流线弯曲时，由于离心力的变化产生二次流，有线垂直方向的河床附近流速可使用如下公式：

(10)

式中，rs—流线的曲率半径，m；N*—二次流动强度因子，在本研究中，采用Engelund(1974)提出的7.0，该值是在弯道处为侧坡平缓时获得的。流线的曲率如图1所示。

图1 用于定义流线和曲率半径的示意图

在此，作为数值分析技术，动量方程式在交错网格中的对流项是称为Yabeetal提出的高阶Godunov方法的CIP(立方粒子)。对于扩散项，采用了中心差法(Jang和Shiizu，2005)，为了分析流动方程，在上游确定了流速，在下游确定了深度。为了防止冲刷，假定是固定河床底，在侧壁上假定没有垂直流动，在流动方向上作为滑动条件。

3 数值模型的应用

3.1 数值模型验证的数学实验

为了审查此数值模型的适用性，将结果与Chang-Rae Jang等(2008)进行的室内试验结果进行了比较。试验通道的大小为12m长，0.9m宽，0.6m高，使用地下储层中的泵进行测试。在配备有循环水系统的可变坡度运河进行室内实验，该循环水系统由上游的水箱供水。在闸门的下游端安装了一个闸板，可以调节下游的水位。水道的左侧壁由丙烯酸板制成，因此可以在试验过程中看到水道的内部，而右侧壁由钢制成。

为了进行流动相实验，使用自制的撒砂机将20cm的厚度的沙均匀地铺在测试通道的底部。当选择用于移动床室内试验的床土时，试样不得因实验过程中的表面张力而独立移动或上升至高于水面的高度，不得漂浮。

在试验过程中，在上游端不断供应土石料，防止在水道入口处出现局部冲刷，并保持床层移动平衡。排水后，使用电子点规在从上游2m到下游10m的横向间隔为5 cm，纵向间隔为20 cm的范围内进行测量，并继续进行试验，直到采集点(疏浚点)挖出的坑被完全填满为止。在试验过程中，为准确记录流路的波动，在测量床高之前和之后立即拍摄了照片，参数条件见表1。在此，描述了根据河床坡度变化对水池的适应过程。与河床坡度变化有关的试验是RUN1和RUN2，根据采集点(疏浚点)挖出的坑大小的变化来掌握河床平衡过程的试验是RUN2和RUN3。

表1 试验和数值模拟的水力参数

图2显示了RUN3随时间推移而重新填充的水坑的图像，底部挖掘点距上游4m，水坑长2m，宽0.5m，深0.1m。图2(a)开始运行后，在水坑异常水流处发生了快速的水头侵蚀，并向上游扩散。随着水波向上游扩散，水头变小，减少了水头侵蚀，水坑被上游提供的沙土填充，如图2(b)所示。在水坑的形状保持恒定的同时，在流动方向上重新填充水坑，如图2(c)所示。

图2 RUN3的试验结果

3.2 数值模拟条件

为了审查该数值模型的适用性，将平面和地下通道的变化以及水坑的运动特性与室内试验的结果进行了比较，表2列出了用于进行数值模拟的参数。每个参数的值是通过考虑基础道路的物理特性确定的。用于数值模拟的计算网格由河流的纵向60个网格和横向的20个网格组成，纵向网格的大小在横向上分别为0.2m和0.045m，长宽比为4.4(图3)。

图3 数值模拟的计算格

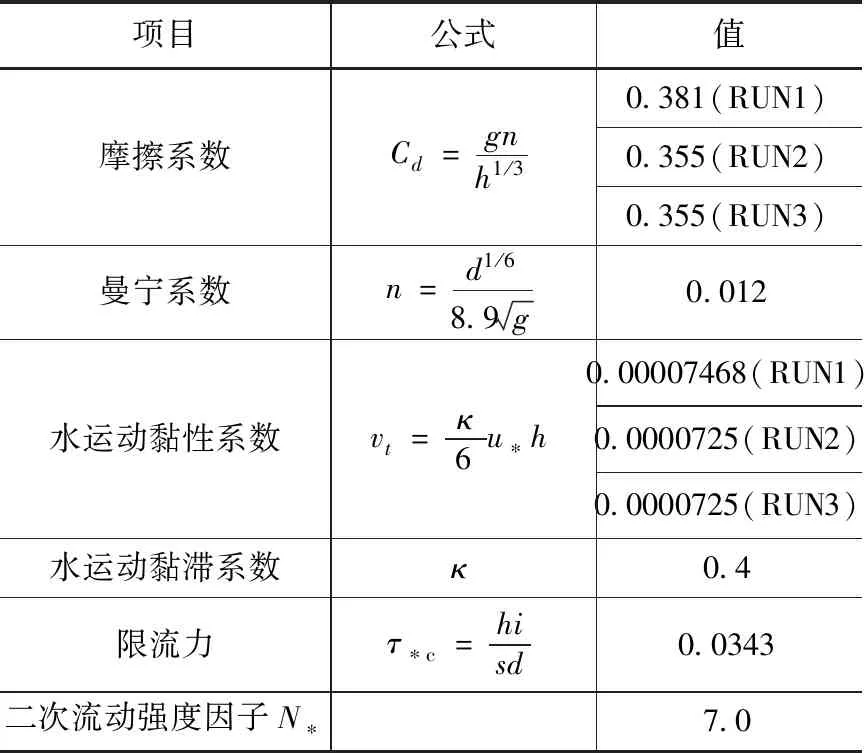
表2 数值模拟的参数

3.3 数值模拟验证结果

图4显示了通过RUN2的河底采集点(疏浚点)水坑平衡过程的室内试验和数值模型。当水开始流动时，采集点(疏浚点)水坑处的紊流迅速侵蚀了水头。随着时间的增加，由于上游提供了沙，采集点(疏浚点)水坑侵蚀减少了。沙几乎被水坑捕获，几乎没有沙转移到下游子池中。水坑保持了恒定的休止角，并且在子池中形成了无腐蚀侵蚀[图4(a)]。经过120min的注水，水坑的回填向下游移动约0.4m[图4(b)]，并发生了水流分离。

图4 RUN2在不同试验条件下的对比(水流从左至右)

图5显示了RUN2水坑的纵向高度随时间的变化，沙子在填充水坑的同时保持恒定的水下休止角。数值模拟很好地模拟了这一特性，此外，随着时间的增加，水坑被重新注满，显示出上游河床的轻微振动。

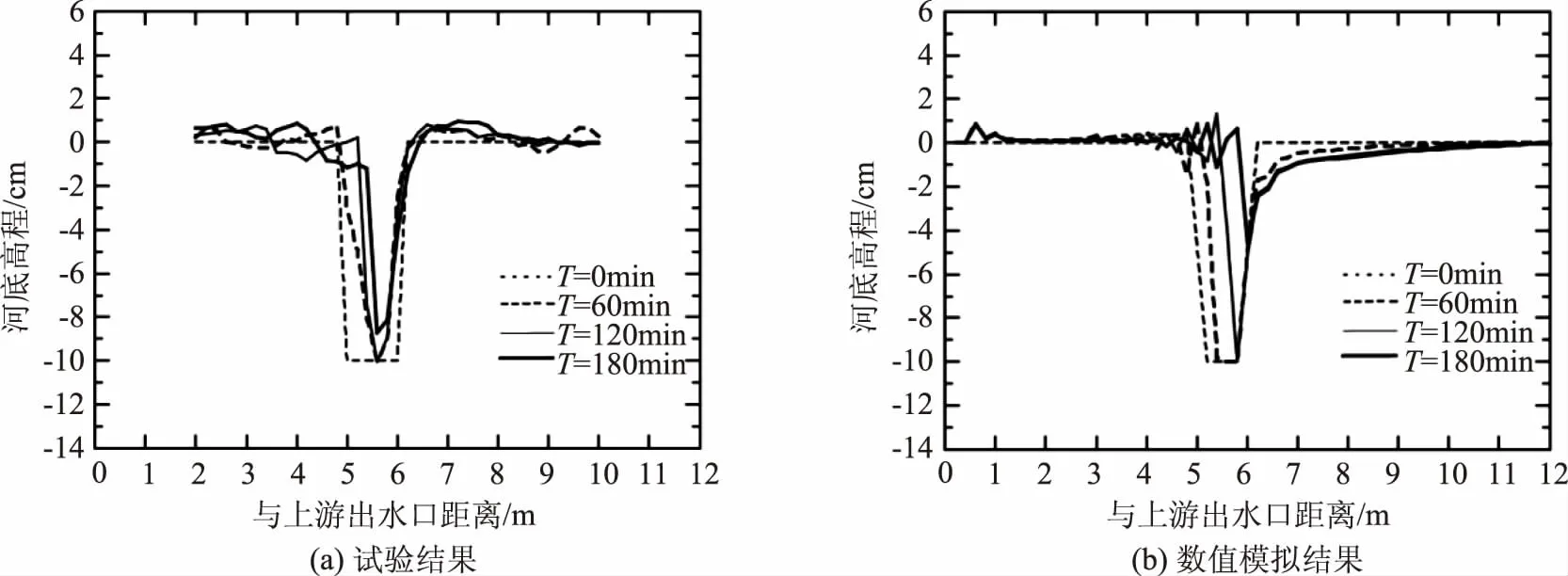
图5 RUN2水坑的纵向高度随时间的变化试验与数值模拟对比

在水坑的回填过程完全完成后的450min内，水坑回填完成时向下游发展，数值模型很好地模拟了该特征，但是水坑的位置位于实验结果的下游约1m处，与RUN2的结果一致，数值模拟的结果比室内实验的结果略微高估了下游子池中微侵蚀的特征。该差异可能是由于数值模型在模拟池中水流的三维特征方面存在局限性。

图6显示了水坑运动趋势的数值模型结果和室内实验结果，对于RUN1，水坑缓慢移动长达30min。这是因为回填完成后水坑的深度会变浅，数值模型通常可以很好地模拟实验结果。在RUN2中，达到平衡的时间是240min，数值模拟结果表明实验结果吻合得很好[图6(b)]。在RUN3中，水坑填充过程中的运动特性也与数值模拟结果和实验结果非常吻合。

图6 沙子在试验条件下和数值模拟的移动对比

图7显示了每个实验的水坑运动速度的数值模拟结果和室内试验结果。对于RUN1，它显示了水坑的移动速度比RUN2的结果要快；对于RUN3，其底坡度是相同的，因此，水坑的平均移动速度与RUN2的结果几乎匹配。

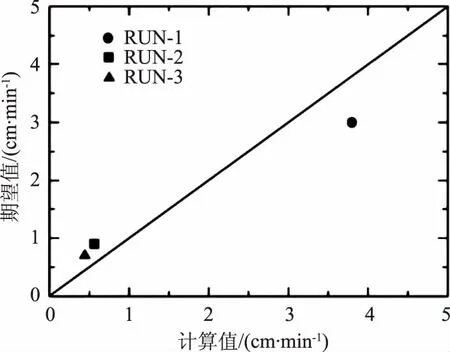
图7 沙子在试验和数值模拟下的移动速度

4 结论

本研究模拟了总坐标系中的水流和河床波动，定量地确定了根据土石料采集或疏浚工程中不同规模变化引起的河道响应特征。由土石料采集或疏浚形成的水坑，首先在水坑异常流量点迅速侵蚀，并扩散到上游。随着时间的增加，水坑的侵蚀由于上游提供的沙石而降低，水坑开始重新填充，水坑被上游提供的沙石填充，同时保持一定的休止角并以几乎均匀的速度移动。数值模拟的结果很好地模拟了这个过程。当然数值模拟在模拟水坑中水流的三维特征方面存在局限性，仅能模拟二维情景。且这种数值模型是在河床坡度较大且池塘尺寸较小的情况下使用的。因此，有必要研究广义的适应过程。