泡沫沥青膨胀率与沥青表面能的相关性分析
宋庆瑞
(山西省公路局 晋中分局,山西 晋中 030600)
0 引言
泡沫沥青冷再生技术作为一种新型的节能环保路面维修技术,在国内外沥青路面养护工程中被广泛应用[1]。沥青的发泡性能是影响泡沫沥青混合料性能和冷再生工程质量的关键因素之一[2],而膨胀率(Expansion Ratio,ER)为泡沫沥青膨胀达到的最大体积与原沥青体积之比,被用作评价沥青发泡性能的重要指标[3]。膨胀率越大代表泡沫沥青表面积越大,在拌和过程中与集料接触面积就越大,进而保证再生混合料拌和均匀性[4]。但在实际工程应用过程中,由于沥青发泡效果不理想进而更换沥青品牌,以致延误工期的情况时有发生。为此,大量研究从沥青种类、发泡温度、用水量[5-6]以及发泡剂[7]等方面分析了各因素对沥青发泡性能的影响,并得出了发泡效果最佳的条件组合。现有研究成果虽然对泡沫沥青冷再生技术的推广应用起到较好的指导作用,但并无从沥青材料本质属性上揭示泡沫沥青膨胀机理。
该研究首先从理论上分析了膨胀过程中泡沫内蒸汽压、沥青膜表面能做功的转换关系,推导了单个沥青泡沫的膨胀率与沥青表面能的函数关系;其次采用WLB.10S型发泡设备联合激光测距技术,实测了4种沥青在不同发泡温度及发泡用水量条件下的发泡曲线,通过发泡曲线计算了泡沫沥青的膨胀率;同时基于躺滴法测定了4种沥青与蒸馏水、甲酰胺、甘油的接触角,进一步计算了4种沥青的表面能;通过建立4种泡沫沥青膨胀率与沥青表面能间的相关性,从试验角度验证了理论推导的函数关系。
1 泡沫膨胀过程理论分析
为分析蒸汽压与沥青膜表面能间平衡问题,首先不考虑沥青泡沫与泡沫间的相互作用,独立分析单个沥青泡沫的膨胀过程。
图1所示,初始半径为r1、表面能为γ的沥青泡沫,由于泡沫内蒸气压P1与外界大气压P0间存在压强差Δp,导致泡沫体积不断膨胀(半径由r1扩张为r2)。因泡沫内部气体物质的量保持不变,假设在膨胀过程中泡沫体系温度保持恒定,则泡沫内部气体体积变化规律满足波义耳(Boyle)定律,即气体的压强与体积成反比关系。因此,在膨胀过程中沥青泡沫体积不断增大,内部压强不断减小,直至系统达到平衡状态。
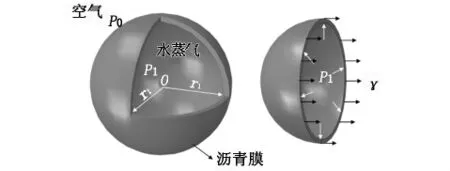
图1 单个泡沫膨胀示意图
泡沫表面积由A1变为A2,泡沫表面能增加量ΔGb为:

式中:A1、A2分别为泡沫膨胀前后的表面积,m2;γ为沥青表面能,J/m2;r1、r2分别为泡沫膨胀前后的半径,m。
泡沫体积由V1变为V2,压强差Δp做功ΔGs为:
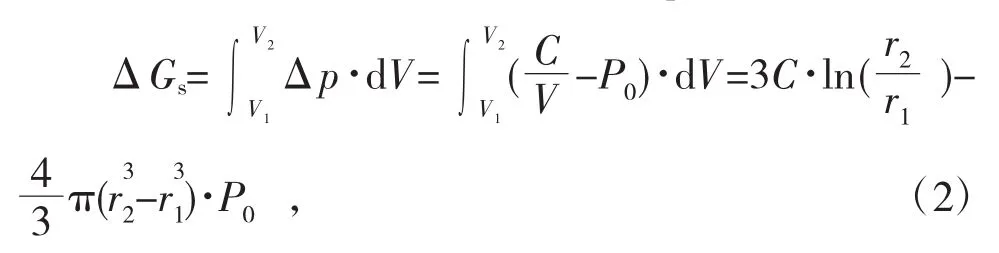
式中:V为泡沫内气体体积,m3;C为波义耳定律常数,Pa·m3;P0为大气压,Pa。
在泡沫膨胀过程中,水蒸气压强差所做的功ΔGs等于泡沫表面能的增加量ΔGb,则有:

假设单个泡沫体积膨胀率为ERs,经膨胀后其半径扩大为则有:
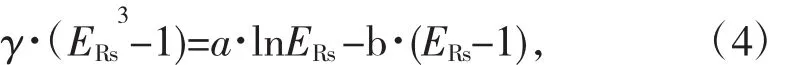
2 试验
2.1 原材料
选用不同品牌的4种石油沥青(QL-70号、ZN-70号、PJ-90号、ZJ-70号),根据JTG E20—2011《公路工程沥青及沥青混合料试验规程》对沥青基本性质进行测试,结果见表1。
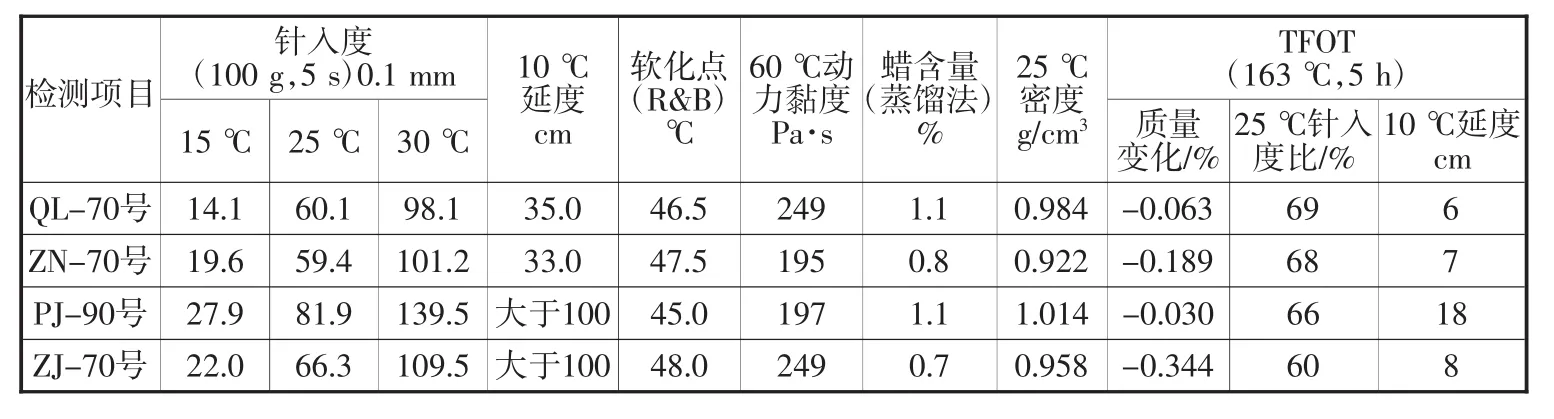
表1 沥青基本性质
2.2 沥青表面能测试
2.2.1 测试原理
基于躺滴法进行沥青表面能参数测试,其基本原理为杨氏接触角方程。杨氏接触角示意如图2。
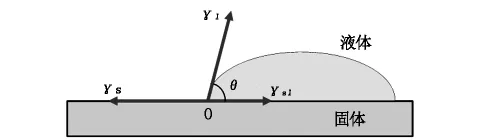
图2 杨氏接触角示意图
当液滴达到平衡稳定状态时,存在如式(5):

式中:γs为固体表面能,mJ/m2;γl为液体表面能,mJ/m2;γsl为固体-液体界面能,mJ/m2;θ为γl与γsl的夹角,(°)。
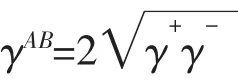
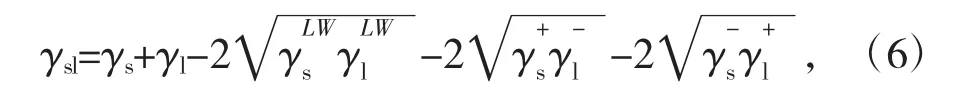
代入Young方程,拓展如下:
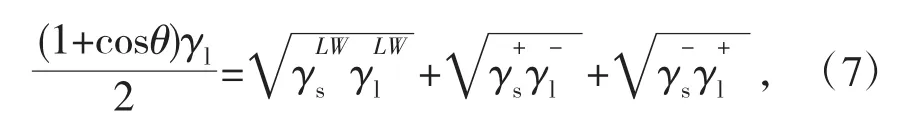
式中:γlLW、γl+、γl-分别为液体色散分量、极性酸分量、极性碱分量,mJ/m2;γsLW为固体色散分量;γs+为固体极性酸分量;γs-为固体极性碱分量。
2.2.2 试样制备及接触角测定
将4种沥青分别加热至163℃备用;采用载玻片作为沥青膜载体,并将其置于烘箱中60℃条件下预热2 h;预热后的载玻片均匀蘸入加热备用的沥青中,缓慢提出后将其平置冷却。化学试剂采用蒸馏水、甘油、甲酰胺,其表面能[9]及相关参数如表2。
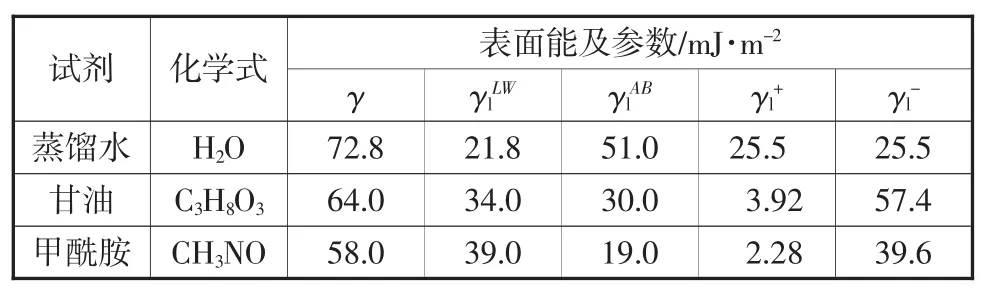
表2 化学试剂表面能参数
2.3 沥青发泡试验
该研究采用维特根WLB.10S型发泡设备进行沥青发泡试验,并基于激光测距技术实时、准确采集沥青发泡与坍塌全过程数据。
3 结果与讨论
3.1 理论关系
为直观表述沥青表面能γ与单个泡沫膨胀率ERs间的关系,依据式(4)对各参数进行赋值,进一步绘制两者关系曲线如图3。参数赋值情况:Biruk[10]采用X射线观测了沥青在发泡过程中泡沫的尺寸分布,认为泡沫形成初期单个泡沫截面积为0.2~10 mm2,该研究取泡沫初始半径r1为0.25 mm;大气压P0取值101.325 kPa;气体物质的量取值0.1 mmol,热力学温度T取值423.15 K(160℃),摩尔气体常数R取值8.314 J/(mol·K),波义耳定律常数项C=nRT=0.360 J。
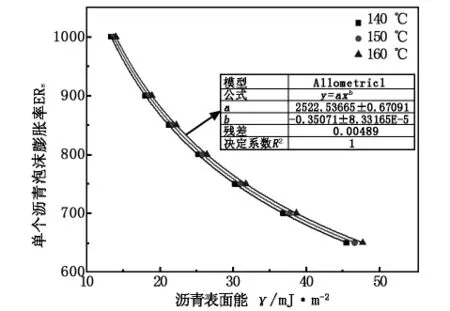
图3 单个泡沫膨胀率ERs与沥青表面能γ的理论关系
图3可知:a)单个泡沫膨胀率ERs与沥青表面能γ的理论曲线中,x轴为沥青表面能,其取值范围为13.33~47.76 mJ/m2,与文献[11]中17种沥青表面能试验统计结果11.28~43.07 mJ/m2基本一致,表明理论曲线赋值的合理性。该研究设定泡沫初始半径r1为0.25 mm,结合关系,可计算得出半径r2的范围为2.19~2.52 mm。文献[12]统计分析了不同温度下沥青泡沫直径的分布,表明发泡温度140℃~160℃范围内,泡沫直径范围为4.6~5.6 mm;与该研究理论计算结果基本吻合。b)单个泡沫膨胀率ERs与沥青表面能呈负相关关系,即随沥青表面能增大,其膨胀率ERs呈降低趋势;且两者间采用幂函数拟合效果较好(R2=1)。
3.2 沥青表面能计算结果
4种沥青与3种滴定液体间的接触角数据分布情况如图4a。另外,验证数据有效性方法[13]如下:对于给定的某一固体,不同滴定液体的γlcosθ与γl存在线性关系,即决定系数R2越大,接触角数据测试越可信。沥青接触角数据有效性检验如图4b。
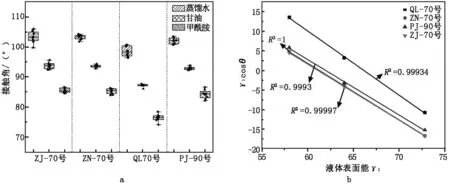
图4 沥青接触角数据分布及有效性检验
图4可知:同种沥青与同一滴定液体间接触角多次测量其数据较为集中,试验结果重现性较好。另外,4种沥青接触角数据有效性检验结果其决定系数R2均大于0.999,说明沥青γlcosθ与γl线性关系显著,数据准确度高。
沥青表面能及分量计算时,由式(7)可知表面能及各分量参数均为非负值,该研究利用Matlab 2018a软件中求非负最小二乘解命令lsqnonneg对所建立的矩阵方程式进行求解。4种沥青表面能及分量计算结果如图5。

图5 沥青表面能及分量计算结果
图5可知:a)实测的4种沥青其表面能γ测试范围为22.053~ 29.441 mJ/m2,平均为24.158 mJ/m2;其中,QL-70号沥青表面能(29.441 mJ/m2)显著高于其他3种沥青。b)4种沥青表面能组成中均呈现相同规律,即色散分量γLW在沥青表面能γ中占比较大(99.8%),而极性分量γAB占比相对较小(0.2%)。该规律与沥青材料组成有关,即表面能参数反映材料本质属性,沥青由非极性碳氢化合物组成,故其色散分量γLW在表面能γ中占主要部分。
3.3 试验验证
采用WLB.10S型发泡设备联合激光测距技术,实测了4种沥青在不同条件下的发泡t-Δh曲线。依据各沥青发泡过程t-Δh曲线,直接获取曲线最大高度hmax,进一步与未发泡状态下沥青高度hv的比值,即可计算出泡沫沥青的膨胀率ER;进而建立沥青表面能γ与泡沫沥青膨胀率ER的相关性如图6。
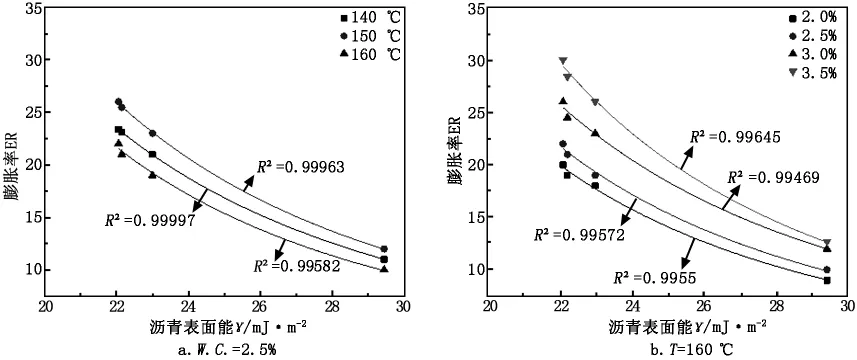
图6 沥青表面能γ与膨胀率ER关系验证
图6a为在相同发泡用水量(2.5%)、不同发泡温度(140℃、150℃、160℃)条件下,泡沫沥青膨胀率与沥青表面能的关系。采用幂函数对其进行拟合,发现其决定系数R2均大于0.99;表明沥青表面能与泡沫沥青膨胀率之间存在较好的幂函数关系,与前述理论分析一致。另外,相同表面能前提下,150℃时沥青发泡膨胀率大于140℃与160℃时的膨胀率,一定程度说明沥青发泡存在最佳发泡条件,而并非温度越高发泡效果越好。发泡温度升高时沥青黏度降低,泡沫沥青膜的流动性增大,进而导致膜体破裂影响膨胀率。图6b为相同发泡温度(160℃)、不同发泡用水量(2.0%、2.5%、3.0%、3.5%)条件下,泡沫沥青膨胀率与沥青表面能的关系。在相同表面能条件下,随发泡用水量增加,泡沫沥青膨胀率ER增大;表明发泡用水量增加有利于产生更多的水蒸气,进而水蒸气压强做功增大,导致泡沫沥青膨胀率增大。综上,泡沫沥青膨胀率与沥青表面能之间为幂函数关系,且随沥青表面能增大,其膨胀率呈降低趋势。
4 结语
a)从理论上分析了沥青泡沫膨胀过程中蒸气压做功与沥青表面能做功的平衡问题,得出单个沥青泡沫膨胀率ERs与沥青表面能γ间函数关系为:γ·(ERs3-1)=a·lnERs-b·(ERs-1),其中a和b为与泡沫起始半径r1相关的常数。
b)对膨胀率ERs与表面能γ的函数中各基础参数进行赋值,数值上ERs与γ两者间符合幂函数关系,且决定系数R2=1。
c)实测并建立不同发泡条件下泡沫沥青的膨胀率以及对应沥青表面能间的关系,两者间亦存在较好的幂函数关系;且随沥青表面能的增大,泡沫沥青膨胀率呈降低趋势。

