气泡脱离毛细管时曲率半径的变化规律

彭 宁

(桂林理工大学 化学与生物工程学院,广西 桂林 541000)

在日常生活中,我们会发现一些有趣的现象,例如水珠在洁净的玻璃上会以球形的形状存在、毛细管中液体会自动的上升(水)或下降(汞)而不同于外液面齐平、自来水笔中的墨水不会因地心引力而滴出等,吹出的肥皂泡泡、荷叶或芋叶上滚动的水珠都以球形形式存在,这实际上都与液体表面受到一种作用力有关,即液体的表面张力。表面张力是液体最重要的性质之一,它的形成是由于液体表面分子受力不均匀导致的。如在气-液系统中,由于液体内部分子对液体表面分子的作用力远远大于液面上方气体分子对它的作用力,从而使得液面分子受到指向液体内部的拉力作用,因此液体都有自动缩小其表面积的趋势[1]。而在相同体积下,球形具有最小的表面积,因此液体都有趋向于变成球形的趋势。如若要增大液体的表面,就需要克服所受作用力做功,从力的角度规定沿着表面并和表面相切、垂直作用在单位长度液相界面上的力,称为表面张力σ,单位为N·m-1；而从能量角度分析,为克服液体所做的表面功所需比表面吉布斯自由能的改变ΔG 规定为表面张力,单位为J·m-2。

对平面液体而言,由于液面分子所受的表面张力方向是与液面相切的,无指向液体内部的表面张力的分力,因此液面下方的液体分子所受到的压力即为外界环境对液体的垂直压力；然而,对于弯曲液面而言,由于液面分子所受的表面张力方向是与液面相切的,由于液体表面张力的存在且表面液体分子所受合力不为零,会在弯曲液体表面产生一个合力,并且该合力方向指向弯曲液面的中心点。因此,由于表面张力的合力不为零并且指向弯曲液面的中心,导致液面两侧的压力并不相等,最终在弯曲液面下方的液体受到来自液面产生的附加压力ΔP 的作用,显然附加压力的大小与表面张力的大小具有紧密联系。对于水滴等凸液面而言,该附加压力为外界压力与弯曲液面所受压力的差值,表达式为ΔP=P外-P内=Pg-Pl,其中Pg为外界环境中的大气压力,Pl为凸液面本身所受的压力Pl；相反,对凹液面而言,即对液体中存在的气泡来说,该附加压力仍然为外界压力与弯曲液面所受压力的差值,表达式为ΔP=P内-P外=Pg-Pl,其中Pg为气泡内的压力,Pl为凹液面所受的压力。基于拉普拉斯方程,可以获得附加压力ΔP,表面张力σ 及弯曲液面曲率半径r 之间的关系为ΔP=2σ/r,因此如若能够通过实验方法获得某一液体的ΔP 和r 的数值,将其代入到上述方程式即可求出该液体的表面张力大小[2]。

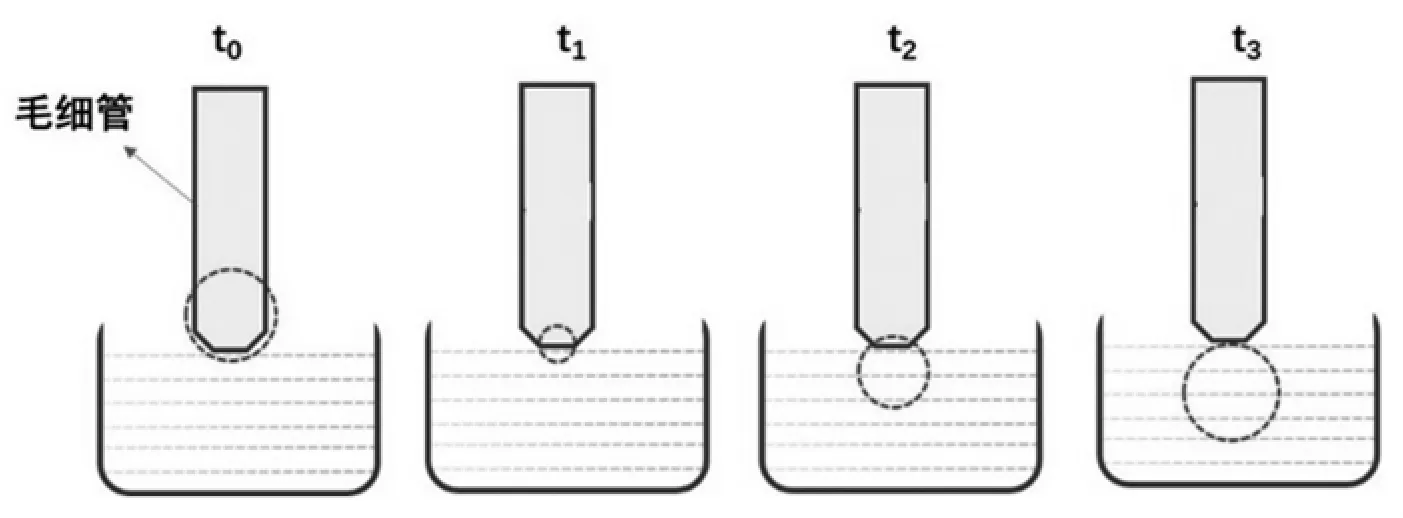
图1 毛细管端气泡形核-长大直至脱离的过程示意图

通常测定溶液表面张力的方法较多,如毛细管升高法、滴体积法、拉环法等,而较为常用的方法为最大泡压法。该方法利用毛细管端的气泡从形核-长大-脱离过程中测量气泡所受的最大附加压力值来求得液体的表面张力。首先来考察一下气泡的形成过程,如图1 所示,为毛细管端气泡从形核(t0)到长大(t1、t2)最后从端口脱离(t3)过程的示意图,可以发现在整个过程中,气泡曲率半径r 的变化为从开始的平面,即r 为无穷大逐渐减少直至最小值,此时曲率半径即为毛细管端的半径,然后在逐渐增大至极大值直到气泡瞬间脱离毛细管断口并上升逸出[3]。通过分析可以发现,在气泡曲率半径为毛细管端的半径时,由拉普拉斯方程可知,此时对应的附加压力ΔP 为最大值,通过数字微压差仪可以读出该最大的附加压力值,再把读取的数值和对应的毛细管的半径代入到拉普拉斯方程即可求得液体的表面张力,这就是最大泡压法测定液体表面张力的基本实验原理。液体的表面张力与温度、压力和相互接触两相物质的性质、组成等有关。一般地,随着温度的升高(促使分子间距增加,相互作用减弱)、压力的增大(使两相物质的差异缩小),表面张力都会减少；此外,当在液体中加入溶质后,液体的表面张力也会发生变化,如在水中加入氯化钠、蔗糖等溶质会使表面张力升高,而诸如乙醇、高分子表面活性剂等的加入会使表面张力降低。在现阶段本科实验教学过程中,对该实验的要求和目的为掌握最大气泡压力法测定溶液表面张力的原理和技术,包括测量出纯液体和不同浓度溶液的表面张力即可。所需要用到的仪器一般包括表面张力测定装置(包括带恒温夹层的具支试管、毛细管、滴液漏斗、广口瓶、数字微压差仪),超级恒温槽,烧杯等；所需用到的试剂包含蒸馏水、不同浓度的N-N-二甲基甲酰胺水溶液(分析纯)。

然而,在长期的教学实践中我们发现,同学们会非常好奇气泡从毛细管端脱离后,其脱离尺寸的大小具体为多少,毛细管的半径的不同是否对气泡的脱离有影响。而感兴趣的原因是同学们在平常的生活中都玩过如下游戏：在水中加入适量的洗衣粉,混合均匀后制成肥皂水溶液,用圆珠笔外壳的一端蘸肥皂水后用力吹,能够吹出不同形状的气泡；但如果用半径尺寸大的圆珠笔外壳时,发现并不能够吹出气泡,表明如若要吹出气泡需要合适的毛细管半径。那么,毛细管半径与气泡脱离时的尺寸半径究竟有何联系呢？面对学生们的疑问,一般的实验指导教材中并未有过明确的计算方法,学生们在如何计算气泡的脱离尺寸大小时,常常疑问重重,或面对问题无从下手。基于此,为了解决上述问题,本文将详细探索推导出气泡脱离时的尺寸半径,从而让学生们不仅仅掌握表面张力的测量技术,同时也可以更为深刻地理解和掌握在该过程中气泡尺寸变化的整个过程。如图2 所示为气泡从毛细管端脱离瞬间的受力分析示意图,单纯考虑气泡脱离毛细管端的受力,此时气泡受到液体对其的浮力F浮作用,此外在脱离毛细管瞬间,吸附于毛细管底端的那一部分气泡膜所产生的向下的压力F压的作用,其作用的垂直面积为πr2,该压力限制了气泡从毛细管端脱离并进行上浮[4]。当该气泡发生瞬间脱离毛细管端时,有：

而我们知道,F浮的计算公式如下：

其中,ρ 为该液体的密度,g 为重力加速度,V排为气泡排开液体的体积,也即为气泡体积,d 为脱离瞬间气泡的半径。

而对于F压的计算,有如下公式：

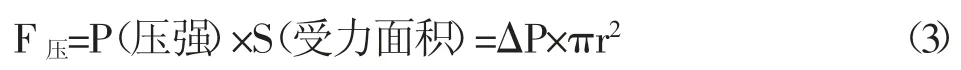
其中,ΔP 为气泡表面张力所产生的附加压力,r 为毛细管的半径。

利用拉普拉斯方程,将方程带入到上述方程(3)中可以得到F压=2σπr,将该方程和上述方程(2)代入到方程(1),我们可以得到：

化简后,即可得到气泡脱离毛细管时的半径d 的计算公式为：

如公式(5)所示,即为气泡从毛细管端脱离瞬间,该气泡所获得的最大半径d 的计算公式。通过方程(5)我们发现,液体的表面张力σ、毛细管端的半径r 对气泡所获得的最大半径具有正影响；而液体的密度ρ 及重力加速度g 对其具有负影响。因此,毛细管端半径r 越大,气泡需要脱离毛细管端的半径也需要越大。但是,过大的毛细管半径要求毛细管端口初始形成曲率半径大的弯曲液面,这对于粘度或弹性很差的气泡膜来说是很困难的[5]。因此,当我们用圆珠笔外壳蘸肥皂水吹气泡时,圆珠笔外壳的半径尺寸不能够过大,以避免不能够形成初始的气泡膜。

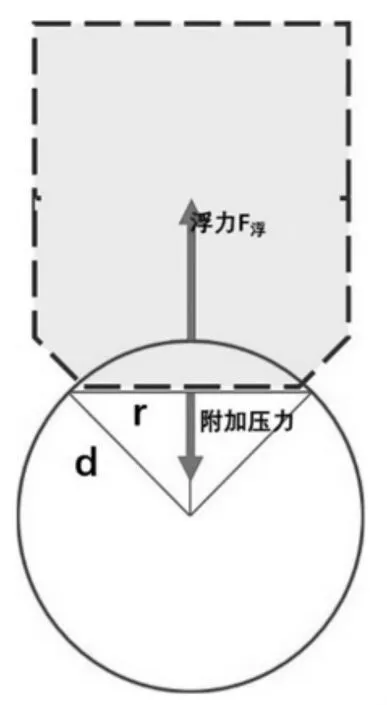
图2 气泡从毛细管端脱离瞬间的受力分析

综上所述,本文基于多年的物理化学本科教学实验的进一步思考,立足于学生们对最大泡压法测量液体表面张力本科实验教学过程中的疑问,尝试进一步探索气泡从毛细管端脱离瞬间其尺寸的大小计算。基于对气泡的受力分析,确定了在单一因素影响下气泡脱离毛细管端面时气泡尺寸的计算公式。作为对该实验的一些探索性分析,对实验教学研究中学生们感兴趣的一些问题做了初步讨论和回答,在针对该实验教学上具有一定的价值,能够让学生们更为深刻地理解毛细管端气泡从形核-生长直至脱离的整个过程,激励学生们从兴趣出发,勇于探索分析日常生活中遇到的问题并用相应的科学原理和科学方法进行分析和解决。