差分自回归移动平均模型在南通市手足口病疫情预测中的应用

练 维，魏 叶，韩颖颖，帅小博

1南通市疾病预防控制中心科研质量管理科，2急性传染病防制科，3慢性非传染病防制科，江苏 南通 226007；4南通市崇川区疾病预防控制中心检验科，江苏 南通 226000

手足口病（hand⁃foot⁃mouth disease，HFMD）是一种病毒性的急性传染病，1980年在我国广州首次报道［1］，2008年被列为法定丙类传染病，它由包括柯萨奇病毒、新型肠道病毒、埃可病毒等在内的20 余种肠道病毒引起，其中又以肠道病毒71 型（EV71）和柯萨奇病毒A组16型（CoxA16）最为常见，一直为优势流行毒株，这两者可交替或者共同传播［2］。但近年来，由柯萨奇病毒A 组6 型（CoxA6）、柯萨奇病毒A 组9 型（CoxA9）、柯萨奇病毒A 组10 型（CoxA10）、埃可病毒11型（ECV11）等引发的疫情有上升趋势［3-5］，值得密切关注，5岁以下尤其是3岁以下的儿童是防控的重点人群［6］。本文对2010—2019年南通市手足口病发病情况进行分析，以2010年1月—2019年6月南通市手足口病分月报告病例数据为基础，通过建立差分自回归移动平均（autoregressive integrated moving average，ARIMA）模型［7］，预测2019 年7—12月发病率，并与当时的实际发病率比较，验证模型效果，为南通市手足口病的防控提供策略和技术支撑。

1 资料和方法

1.1 资料

资料来源于中国疾病预防控制信息系统2010年1 月1 日—2019 年12 月31 日南通市常住人口的手足口病监测数据和人口数据。

1.2 方法

以2010年1月1日—2019年6月30日南通市手足口病疫情月报告发病率为基础建立时间序列。手足口病月发病率时间序列为季节性时间序列，故采用乘积季节模型，即ARIMA（p，d，q）×（P，D，Q）S。其中d为平稳化过程中差分的阶数，p、q分别为自回归阶数和移动平均阶数。P、Q分别为季节自回归和移动平均阶数，D为季节差分阶数，s为季节性周期循环长度。模型建立的步骤分为：①确保时序的平稳性。平稳性是ARIMA模型中的一个重要假设，一般可通过时间序列图直观判断。对于不平稳时序，则需要通过数据变换和差分使序列满足平稳性假定，并使用ADF统计检验来验证平稳性假定。②模型识别和定阶。根据平稳化后序列的季节差分自相关（ACF）函数图和偏自相关（PACF）函数图，进行模型的识别和定阶。③模型的参数估计和检验。使用非线性最小二乘法估计模型的参数，Ljung⁃BoxQ统计量检验，P＞0.05，提示残差是白噪声序列，反之为非白噪声序列。④评价模型预测效果。利用非参数检验法（两个独立样本检验法），对2019年下半年实际月发病率与预测月发病率进行比较，评价模型预测效果。

1.3 统计学方法

运用Excel2007 建立和管理数据库，运用SPSS 25.0 软件进行统计分析和模型构建，分类资料采用例数和构成比进行统计描述；采用非参数检验法对率进行比较：利用χ2检验对不同型别手足口病阳性检出率进行比较，利用两个独立样本检验法对手足口病实际发病率与预测发病率两组数据进行比较，以P＜0.05为差异有统计学意义。

2 结果

2.1 手足口病发病情况

2010—2019年南通市共报告手足口病90 766例，年平均发病率为124.36/10 万，其中2018 年发病率最高，为235.29/10万（图1）。

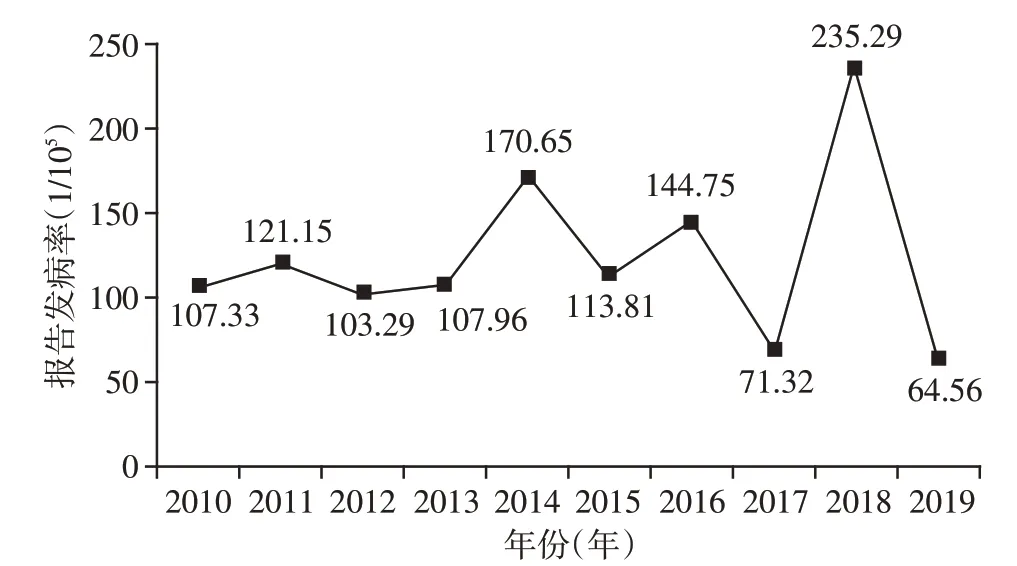
图1 2010—2019年南通市手足口病发病率Figure 1 The morbidity of HFMO in Nantong from 2010 to 2019

2.2 病原学检测结果

2010—2019 年90 766 例中实验室诊断病例数为2 950 例，其中EV71 阳性757 例，占25.75%；CoxA16 阳性925 例，占31.4%；其他肠道病毒阳性1 268例，占42.9%，不同的阳性型别检出率比较，差异有统计学意义（χ2=206.95，P＜0.01）。不同年份间EV71、CoxA16和其他肠道病毒阳性检出率差异均有统计学意义（χ2值分别为365.20、119.06、334.47，P均＜0.01，表1）。

2.3 时间分布情况

2010—2019 年，每个月份均有病例发生，经统计，2014 年和2018 年发病水平较高，总体上2 月份发病数最少，6 月份发病数最多，有明显季节性，呈双峰特征，为夏季（5、6、7月）高峰和冬季（11、12月）次高峰，从2013年起，有隔年高发、偶数年份增强的流行特征（表2）。

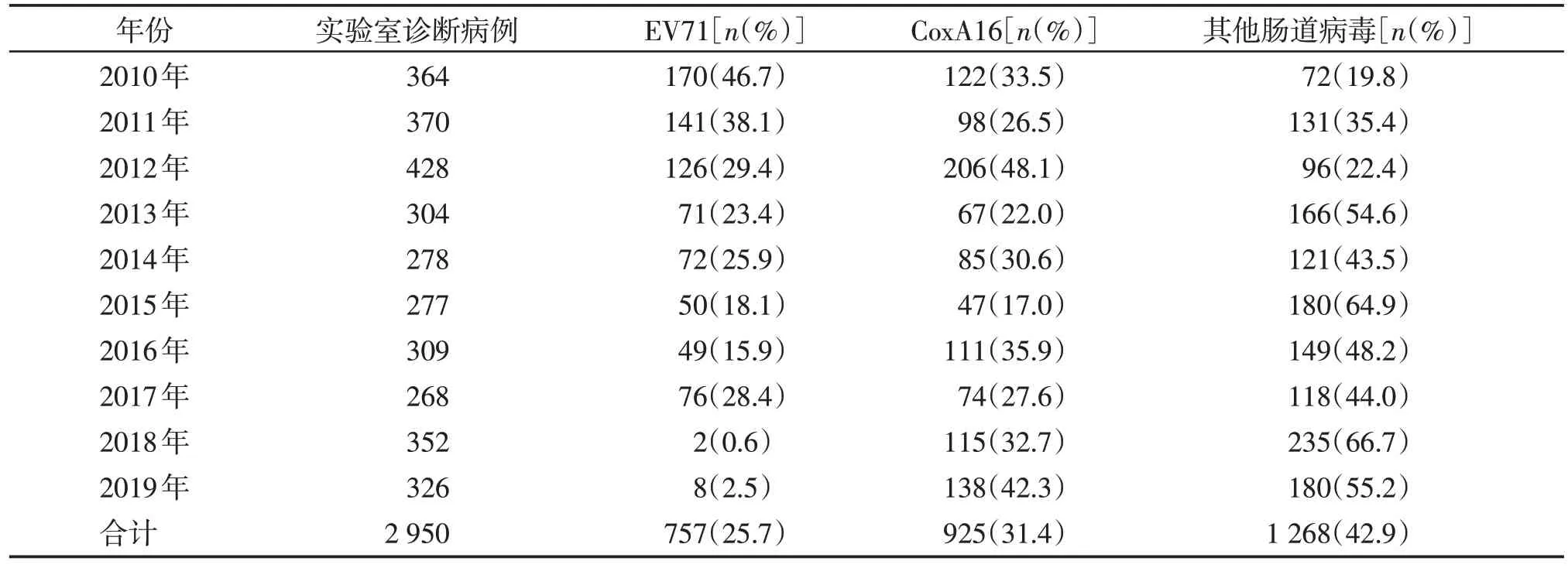
表1 2010—2019年南通市手足口病病原学检测结果Table 1 The results of etiological detection of HFMO in Nantong from 2010 to 2019

2.4 预测模型构建

以2010年1月—2019年6月南通市手足口病分月报告病例数据为基础，构建符合季节性时间序列的ARIMA（p，d，q）×（P，D，Q）S模型，获得2019年7—12月发病预测值，然后用2019年7—12月全市手足口病月发病率为验证数据进行验证，并绘制实际值和预测值序列图。估计预测值与实际值相对误差来判断模型的预测效果。

2.4.1 序列平稳化和预测模型识别

2010年1月—2019年6月南通市手足口病月发病率时间序列图存在以12 个月为1 个周期的季节性波动趋势（图2），不能满足平稳化的要求，需对数据进行平稳化处理；通过对原序列进行一阶季节差分处理后，时间序列ACF 和PACF 函数无明显截尾和拖尾的现象（图3、4），亦无线性衰减，差分后的时间序列图接近平稳，提示差分后序列适合时间序列模型，确定模型为ARIMA（p，d，q）×（P，D，Q）12。

2.4.2 模型的参数估计和检验

根据序列平稳化处理过程，确定模型的d 和D值分别为0和1；根据手足口病的季节性调整，确定s为12；根据ACF函数图和PACF函数图，确定模型的p和q值均为1。模型中的P、Q值分别取0～2由低阶到高阶逐个进行摸索试验。采用Ljung⁃Box 方法检验残差白噪声，若为非白噪声模型则排除。通过筛选，模型ARIMA（1，0，1）（1，1，1）12标准化的贝叶斯信息量（BIC）值为3.59，在模型中最小，R2=0.83，较大，残差序列的自相关系数及偏自相关系数均落在95%CI 中，Ljung⁃BoxQ=19.77，P=0.14＞0.05，提示残差是白噪声序列，确认ARMIA（1，0，1）（1，1，1）12模型最优，可以使用。对该模型的参数进行检验，差异均有统计学意义（P＜0.05，表3）。

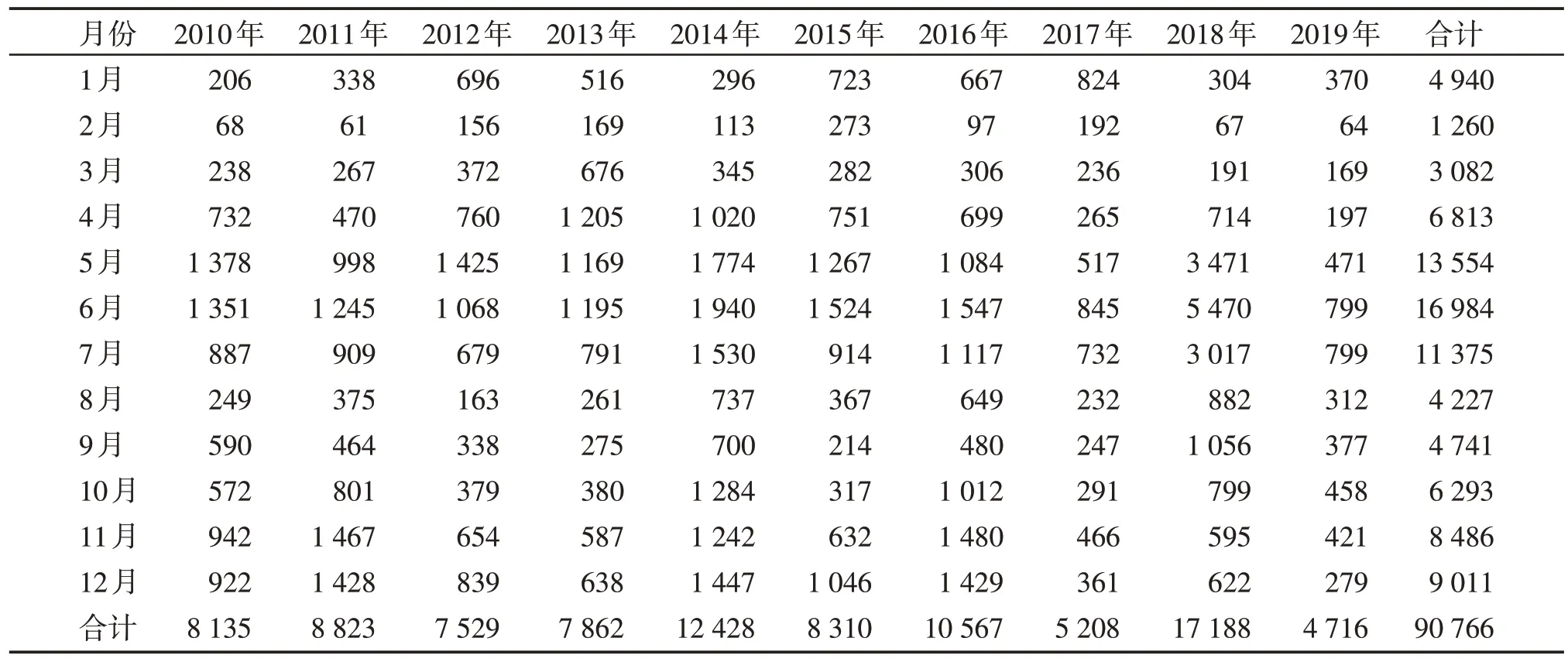
表2 2010—2019年南通市手足口病各月份发病情况Table 2 Monthly incidence of HFMO in Nantong from 2010 to 2019 （例）

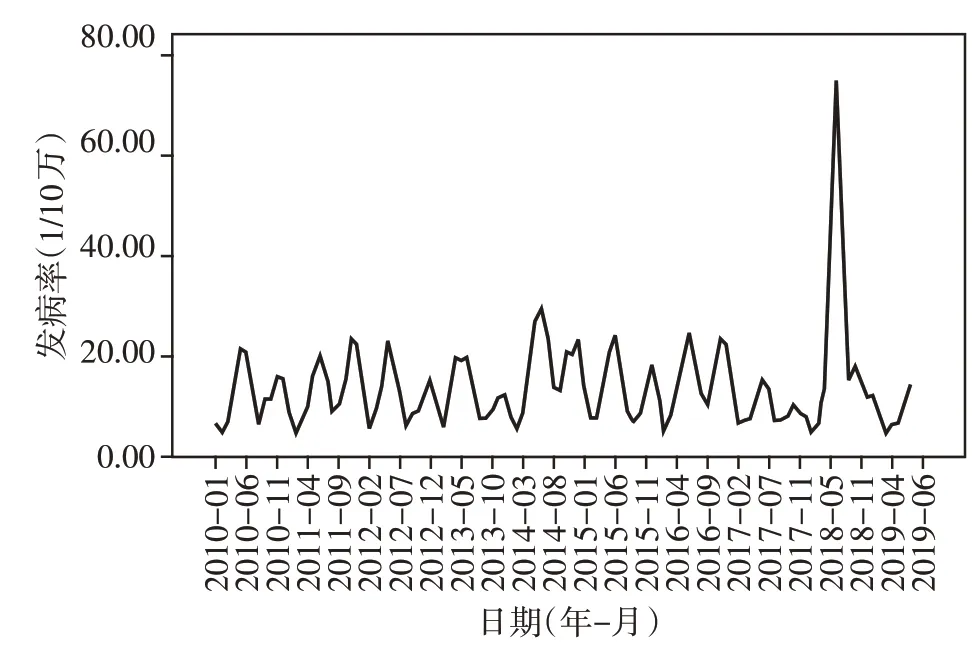
图2 2010年1月—2019年6月南通市手足口病月发病率时间序列图Figure 2 Time series plot of the monthly morbidity of HF⁃MO in Nantong from January 2010 to June 2019

图3 2010年1月—2019年6月南通市手足口病月发病率季节差分自相关（ACF）函数图Figure 3 Seasonal difference autocorrelation function graph of the monthly morbidity of HFMO in Nantong from January 2010 to June 2019

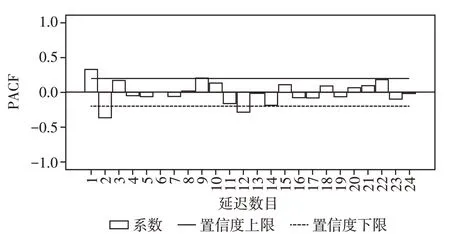
图4 2010年1月—2019年6月南通市手足口病月发病率季节差分偏自相关（PACF）函数图Figure 4 Seasonal difference partial autocorrelation func⁃tion graph of the monthly morbidity of HFMO in Nantong from January 2010 to June 2019

2.4.3 预测模型的效果

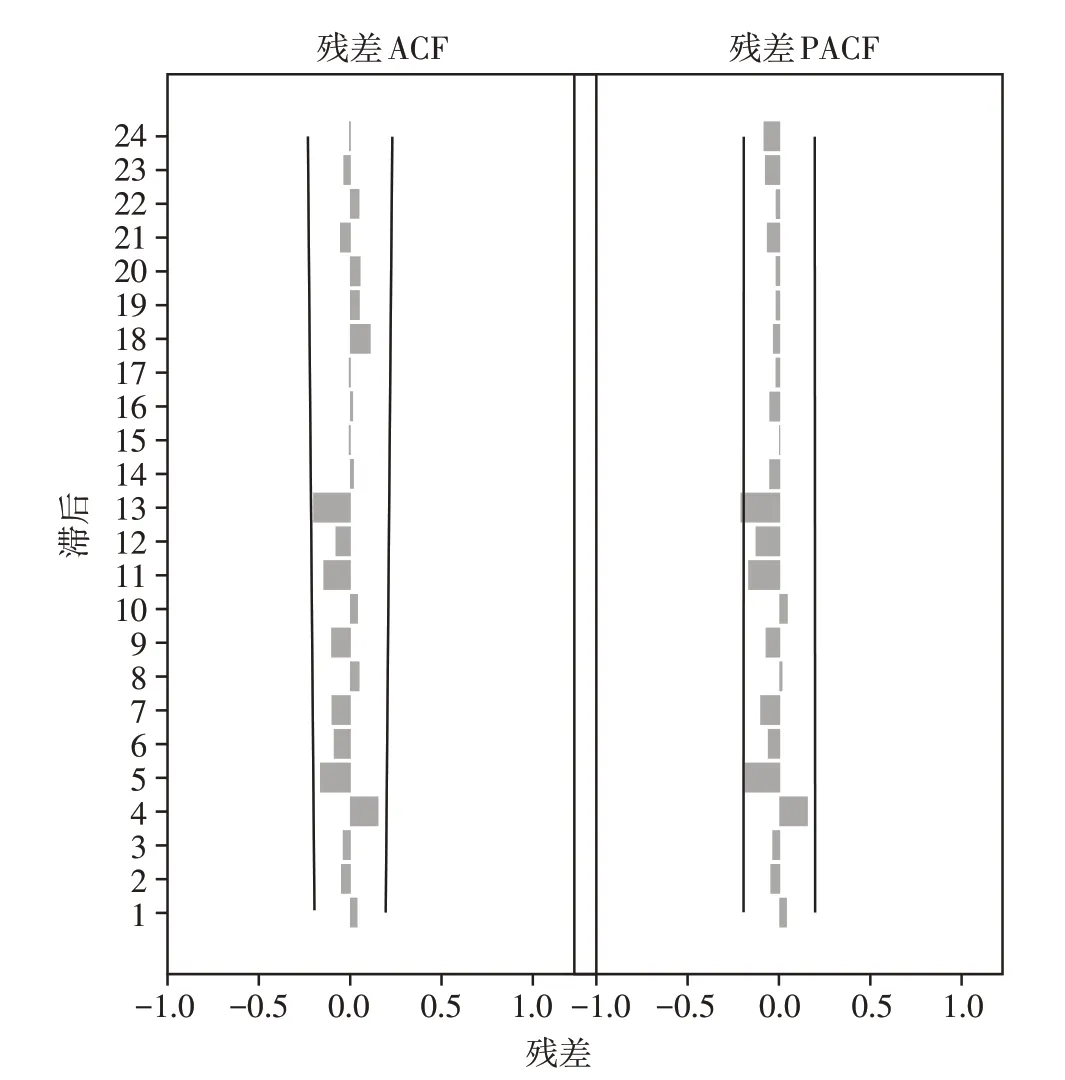
图5 模型ARIMA（1，0，1）（1，1，1）12残差序列的自相关与偏自相关图Figure 5 Autocorrelation and partial autocorrelation function graphs of ARIMA（1，0，1）（1，1，1）12 model residual sequence

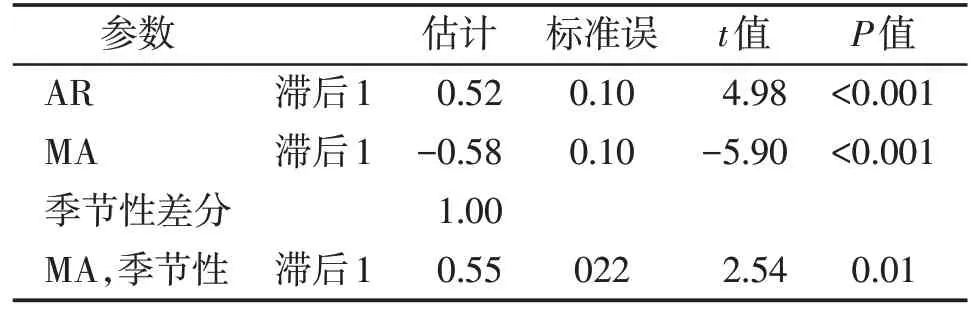
表3 ARIMA（1，0，1）（1，1，1）12模型参数估计Table 3 Parameter estimation of ARIMA（1，0，1）（1，1，1）12 model

通过ARIMA（1，0，1）（1，1，1）12模型对2019 年7—12 月手足口病发病率进行预测，预测结果分别为7.08/10 万、1.81/10 万、3.74/10 万、7.21/10 万、10.71/10万和11.29/10万，绘制实际值和预测值序列图（图7）。

采用两个独立样本检验法，比较2019 年7—12 月手足口病实际发病率（10.96/10万、4.30/10万、5.15/10 万、6.25/10 万、5.83/10 万和3.82/10 万）与预测值的差异，经分析两者间的差异无统计学意义（Z=0.48，P=0.63），预测数据与真实值比较接近，因此该模型有较好的预测效果。

3 讨论

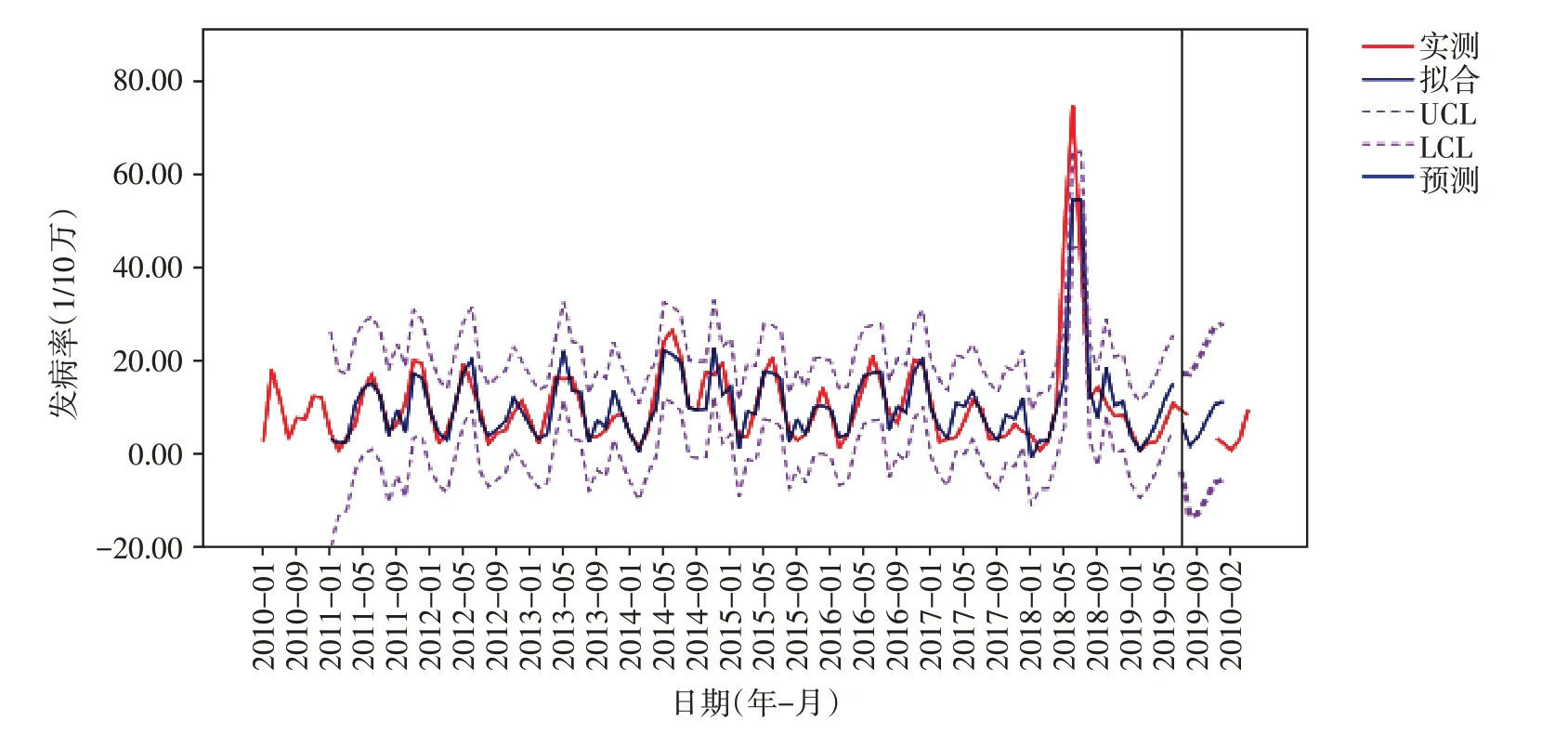
图6 ARIMA（1，0，1）（1，1，1）12模型拟合图Figure 6 Fitted figure of ARIMA（1，0，1）（1，1，1）12 model

本研究结果显示，2010—2019 年南通市手足口病年平均发病率为124.36/10万，低于同时期苏州［8］、无锡［9］和全国［6］平均发病水平，整体呈现隔年高发、偶数年份增强的流行特点。值得关注的是相比往年，2017 年发病率有较明显下降，但随后2018 年出现最高峰，2019年又出现类似情况，按照本市手足口病的流行规律，2020年仍有很大概率出现发病高峰，这可能与易感人群的积累有关［10］。因此做到关口前移，提前做好宣传防控并加大疫苗接种的覆盖率很有必要。

从病原学检测结果来看，2010—2012年引起南通市手足口病的主要病原体为EV71 或CoxA16，从2013 年起转变为其他肠道病毒，这种变化趋势与国内其他地方报道相一致［11-12］。从2010—2019年各月份发病数来看，疫情有明显季节性，呈双峰特征，为夏季（5、6、7月）高峰和冬季（11、12月）次高峰，亦符合我国大部分省份手足口病的发病模式［13］，究其原因，主要是5、6、7月气温适宜，湿度较大，有利于肠道病毒的生存和繁殖，而11、12月儿童的自身免疫力下降。

由于肠道病毒各型之间没有交叉免疫力，且病原体类型较多，传播途径复杂，造成了手足口病反复感染，发病率一直居高不下。因此提前建立预警模型，进行预警分析，进而采取相应措施就显得很有必要。ARIMA模型主要用于拟合具有平稳性（或者可以被转换成平稳序列）的时间序列，最早由Box和Jenkins提出，属于时间序列模型，在手足口病、肺结核、猩红热等传染病的预测中得到了广泛的应用，具有较高的实际价值［14］。本文以2010年1月—2019 年6 月南通市手足口病月发病数为基础，通过序列平稳化、预测模型的识别、预测模型的参数估计和检验，构建了ARIMA（1，0，1）（1，1，1）12模型，最终模型的预测结果与实际拟合度较高，表明该模型对手足口病的流行趋势预测有很好的适用性。尽管其具有拟合度较好、适用性强的特点，尤其对周期性、季节性的传染性疾病有明显优势，但也存在一定局限性，比如只能应用于短期预测，一般不超过时间序列的10%［15］，受外部因素影响［16］等。有资料显示，手足口病的发病与温度、湿度等气象因素以及人口密度呈正相关［17］，并由此衍生了空间累加非线性时空、空间贝叶斯风险评估等一系列模型，提示在今后的实际应用中，可将更多的影响因素纳入手足口病的预警系统，进一步优化模型，从而提高模型的整体预警效果。