可调频悬臂梁式动力吸振器多频减振研究

陈文华，牛军川

（1.中国船舶科学研究中心，江苏 无锡214082；2.山东大学 机械工程学院，济南250061）

手持打磨工具广泛应用于机加工生产中，其工作过程中振动大，存在多个低频线谱，容易引起手部不适导致职业病。常用的解决方案中，阻尼减振对低频线谱控制效果不好，佩戴防护手套影响操作性，而设备的重新优化改进周期长、投入大，均不是最佳方案。动力吸振器（Dynamic vibration absorber,DVA）是进行窄带振动控制的有效措施，对多个振动线谱的控制需要附加多个子结构。而手持打磨工具安装空间小，传统的“弹簧—质量”形式动力吸振器频率不易调节，多子结构的集成性不好，目前缺少适用于手持打磨工具多频减振的动力吸振器。

悬臂梁结构可用于动力吸振，有学者利用悬臂梁自身的多模态进行振动控制[1-3]，经验证能够在多个频率起到减振效果。然而利用悬臂梁自身模态进行振动控制的效果有限，虽然能够实现多频减振，但不能有效地调频，不适合实际工程应用。多重动力吸振器既可以对单一频率进行设计提高减振效果，又可以针对多个频率同时进行减振设计，是进行多频减振的有效方案。目前有关多重动力吸振器的研究[4-5]大多是针对单一频率，分析多重动力吸振器在提高单频减振效果、拓宽减振频域上的优势。但是缺少多重动力吸振器子结构耦合对振动特性影响的讨论，以及针对多个频率进行振动控制的有效性分析。

本文以频率可调、可多频吸振为目标，提出一种适用于手持打磨工具的悬臂梁式动力吸振器，该设计能够根据实际需求进行频率调节，多子结构的集成性好。然后根据结构阻抗特性分析子结构耦合对系统振动特性的影响，最后结合动力学仿真与实验验证了多频减振的有效性。

1 动力吸振器减振原理

从结构阻抗角度分析动力吸振器的作用，对于单自由度系统，主系统质量m1受到激励力F的作用产生振动，其位移变化为x1，则有：

式中：Z1为主系统的速度阻抗。如图1所示。可知：

式中：ω为角频率。为控制其振动，在主系统上附加动力吸振器结构，形成了多自由度系统。主系统振动引起动力吸振器附加质量m2随之振动，其位移变化为x2，m2的振动满足关系：

由此得到x1与x2存在关系：

动力吸振器质量m2的振动提供给主系统一个反作用力f，其大小为

图1 振动系统模型

即添加动力吸振器后引入的附加阻抗大小为

此时振动系统存在关系：

对式（7）进行变形，可以得到：

从式（8）可以看出，主系统质量m1的振动与主系统阻抗Z1及附加阻抗Z2有关，附加阻抗Z2越大m1振动越小。由添加动力吸振器前后的m1振动比值，可以得到插入损失为

从式（9）可以看出，插入损失与附加阻抗呈正相关，附加阻抗越大则振动控制效果越好。为分析系统阻抗特性及动力吸振器的振动控制效果，观察振动系统的阻抗特性如图2，从图2(a)可以看出主系统在固有频率处阻抗幅值最小接近于0，根据式（1）可知此时系统振动最大，即产生共振。图2(b)为动力吸振器的附加阻抗特性，在子系统固有频率处阻抗幅值最大。如将子系统阻抗峰值设计在主系统固有频率位置，根据式（8）可知能够减小主系统的振动。如图3所示为添加动力吸振器后的振动插入损失，可以看出在主系统固有频率位置插入损失最大，即有效地控制了系统共振峰。

图2 振动系统阻抗特性

图3 加入DVA后振动插入损失

2 悬臂梁式动力吸振器设计

2.1 结构设计

本文振动控制对象为手持打磨工具，其振动频谱中存在多个振动峰，对于它的振动控制兼有调频和多频减振的需求。常见的“弹簧—质量”形式动力吸振器由于弹簧刚度不易调节因此频率不可调，且由于安装空间限制难以布置多重动力吸振器，不适用于手持打磨工具。

考虑采用“悬臂梁—质量块”的结构来实现动力吸振，悬臂梁的等效刚度与材料的属性、截面尺寸、悬臂的长度有关系。图4所示为“悬臂梁—质量块”的物理模型，质量块重心到固定端的长度为悬臂梁有效长度。

图4 “悬臂梁—质量块”结构

对该结构进行分析，悬臂梁自由端受集中载荷时，挠度计算公式为

式中：x为悬臂梁的有效长度；E为材料的弹性模量；I为截面惯性矩；Y为自由端挠度；F为集中载荷。因此悬臂梁的等效刚度kbeam为

从式（11）可以看出，通过调节质量块在悬臂梁上的位置，即可改变等效刚度，克服了弹簧刚度不易调节的缺点，达到调频的目的。基于以上分析，可进行悬臂梁式动力吸振器的具体设计。

根据手持打磨工具外形特点并考虑安装的方便性，设计如图5所示的悬臂梁式动力吸振器。悬臂梁上设置有多个频率调节孔，不同位置安装配重对应的频率不同。当振动峰频率变化时，一方面可以调整质量块的安装位置通过改变等效刚度进行调频，另一方面还可以叠加配重改变质量调节频率。该结构能够方便地安装多重动力吸振器，可以对同一频率进行动力吸振器的设计，提高单一频率减振效果；也可以对不同频率进行设计，同时降低多个频率的振动。

图5 悬臂梁式DVA结构设计图

2.2 参数分析

由式（6）可知附加阻抗与动力吸振器子结构的质量和刚度密切相关，而刚度是由质量及设计频率所决定的，因此影响动力吸振器减振效果的主要参数为附加质量的大小。为分析附加质量对减振效果的影响规律，利用动力学软件ADAMS 计算动力吸振器在不同质量比工况下的振动响应，观察减振效果如图6所示。

图6 不同质量比DVA减振效果对比

从图6中可以看出：质量比越大，对于共振峰的抑制效果越好，对应的振动频谱越平坦，减振频域越宽。但是并非质量比越大越好，当质量比为0.1 时，已取得较好的减振效果，继续增加质量则效果提高有限。考虑到应避免质量比过大导致系统重量增加，一般规定动力吸振器的引入质量与原系统质量的比值应小于0.2[6]。

3 减振效果验证

多重动力吸振器的设置一般是为了降低系统对于参数变动的敏感性和提高单一频率的减振效果，但是针对某一频率的振动设置多重动力吸振器会产生资源的浪费，设想如果在多个频率分别进行动力吸振器的设计，将得到多频减振的效果。

根据对某型手持打磨工具的测试，得到其振动特性如图7所示。可以发现在45.5 Hz及81 Hz存在振动峰，采用多重动力吸振器对这两个频率分别进行减振设计。首先确定附加质量，并计算所需的刚度k值，由此确定质量块在悬臂上的安装位置。悬臂梁材料为钢，弹性模量E=2.1×1011Pa，单个质量块质量0.1 kg。根据相关研究内容[7-8]，同时安装两组悬臂梁式动力吸振器时的设计参数如表1所示。

图7 手持打磨工具振动频谱

表1 DVA参数表

3.1 仿真分析

为分析悬臂梁式动力吸振器的减振效果，利用ADAMS进行仿真，对结构添加力激励，观察位移响应。添加动力吸振器前后的振动特性如图8所示。可以看出当添加动力吸振器后，同时有效的抑制了45.5 Hz及81 Hz两个振动峰值。

3.2 实验分析

为分析实际中的减振效果，根据悬臂梁式动力吸振器的设计，进行零件的加工与实验系统搭建，实验测试系统如图9所示。

为排除手部握持力变化对实验的影响，采用固定装置代替人手夹持设备。分别测试设备运行工况下添加单组控制不同频率振动的动力吸振器及同时添加两组动力吸振器的减振效果，着重关注45.5 Hz和81 Hz振动较为突出的频域。

图8 仿真减振效果

图9 实验测试装置示意图

3.2.1 实验等效模型分析

首先对实验系统进行理论分析，根据图9所示的实验设置，将其等效为图10所示的物理模型。将角磨机视为刚体，夹持固定时存在2个自由度，分别是竖直方向的线位移x和相对于水平面的转角θ，分别定义x竖直向下及θ顺时针转动为正方向。

图10 等效物理模型

添加动力吸振器前该系统的运动方程为

式中：m1为角磨机质量；k1为支撑刚度；Jc为转动惯量；G为转动刚度；l1为支撑位置到质心的距离。此时系统位移阻抗为

计算式（13）的矩阵行列式，其特性曲线如图11所示。其中f1和f2对应阻抗为0的频率点，即振动系统的两个固有频率。

图11 原始阻抗矩阵特性曲线

添加动力吸振器后，系统的运动方程变为

式中：l2为动力吸振器安装点到质心的距离；mi、ki分别为动力吸振器的质量和刚度。此时阻抗变为

可以发现添加DVA 后相当于在原有阻抗基础上附加了新的阻抗，从而改变了系统振动特性。对比阻抗Z′与Z0，得到动力吸振器引入的阻抗增量特性曲线如图12所示，其中f3和f4为DVA固有频率。

图12 阻抗增量特性曲线

计算添加动力吸振器前后的系统振动，观察振动控制效果。2自由度系统受迫振动的解为

图13所示为各工况下响应点的振动特性（响应点位移按式(17)定义），可以看出动力吸振器能够有效降低相应频率的振动峰。此外还应注意到动力吸振器对系统其他频率振动特性的影响，从阻抗矩阵可以看出振动系统存在弹性耦合，当仅对其中一个振动峰添加DVA 后，另一振动峰虽未进行减振设计，但依然会受到影响，向低频偏移。图12所示的阻抗增量特性可以解释振动峰向低频偏移的原因：原结构阻抗与阻抗增量相加为0 时会产生振动峰，当添加第一组DVA 时，阻抗增量在f2是正值，会“抬高”原阻抗特性曲线，使得新的振动峰频率向低频偏移；添加第二组DVA时，阻抗增量在f1为负值，会“拉低”原阻抗特性曲线，使得新的振动峰频率向低频偏移。在进行多频减振设计时应考虑到这一影响。

式中：l为响应点与质心之间的距离。

图13 各工况响应点振动特性计算结果

图13中除了动力吸振器幅频特性的典型峰值外，还有A1和A2两种峰值。其中A1是由于阻抗为0而产生的振动峰，而A2是在系统综合作用下产生的减振峰。不同工况下这两种峰值频率也会发生偏移：当同时安装两组DVA 时，相对于单组工况其阻抗增量（正值）在f1附近有些“下沉”，与该区域的原阻抗（负值）相加，则阻抗为0 的点在单组工况的左侧（图11中小图），因此振动峰A1(1)向低频偏移；同理，可解释另一振动峰A1(2)向高频偏移。A1和A2均是在特定参数下产生的，由于理论分析仅作定性分析，其参数设置不是实验系统的精确等效参数，因此这两种峰值在实际系统中未必存在。

3.2.2 实验结果

根据实验设置进行实验，当仅安装第一组控制45.5 Hz振动的动力吸振器时，可以从实验结果图14中看出，降低了45.5 Hz 振动约35 dB，而原81 Hz 的振动峰值未明显降低，略向低频偏移，其原因已在上文进行了解释。

当仅安装第二组控制81 Hz 振动的动力吸振器时，可以从图15中看出，降低了81 Hz处的振动峰值约18 dB，而原45.5 Hz处的振动峰未明显降低，略向低频偏移。

图14 安装第一组DVA减振效果（45.5 Hz）

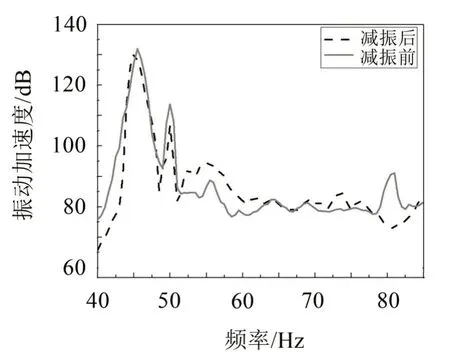
图15 安装第二组DVA减振效果（81 Hz）

当同时添加两组不同频率的动力吸振器时，可以从实验结果的对比图16中看出，动力吸振器同时有效地降低了两个频率的振动。实验中单组DVA工况取质量比为0.1，而为了满足附加质量比小于0.2 的要求，在同时安装两组DVA 时减小了第一组质量比至0.05。由于附加质量减小，45.5 Hz 振动峰减振效果较图14所示的单组DVA控制效果差。

图16 同时安装两组DVA减振效果（45.5 Hz和81 Hz）

为定量分析动力吸振器的减振效果，计算各个工况下40 Hz～85 Hz 频率范围内的振动加速度级，列于表2中。由于振动能量主要集中在45.5 Hz 附近，81 Hz振动峰值较低，因此安装第一组DVA减振效果显著(16.1 dB)，相比较而言第二组DVA 减振效果有限仅为2.3 dB。当同时安装两组DVA时减振效果最好，振动插入损失为17.5 dB，比第一组工况减振效果提高1.4 dB，体现出多频减振的优势。实验结果说明在实际应用中，本文所述悬臂梁式动力吸振器可以发挥减振的作用，且可以同时进行多频减振。

表2 各工况振动加速度级

4 结 语

针对手持打磨工具的振动控制，设计一种可调频悬臂梁式动力吸振器。该设计可根据实际需求进行频率调节，且对多频振动控制的集成性好。根据设计对手持打磨工具采用多重动力吸振器布置方案，结合仿真分析和实验验证了悬臂梁式动力吸振器的实用性，实现了动力吸振器频率可调、可多频吸振的目标。