复杂截面周期性隔振桩带隙特性构型影响因素研究

姜博龙

（中国铁路设计集团有限公司 城市轨道交通数字化建设与测评技术国家工程实验室，天津300308）

在城市轨道交通快速发展、城市土地利用集约化的双重背景下，城市轨道交通线位逐步逼近甚至下穿既有或规划建筑物敏感点，造成了一定的负面影响和经济损失，亟需采取防治措施。当线路开通运营无法更换减振轨道、既有建筑物无法搬迁或加装隔振支座的情况下，传播路径控制具有一定的必要性，对其展开研究具有重要意义。其中，排桩作为一种典型的隔振屏障，被认为在低频隔振中有潜在优势[1]。与此同时，受凝聚态物理及声子晶体的启发，周期结构的带隙特性[2]被引入到隔振排桩的研究中。所谓带隙，是指存在于无限尺寸的周期结构中、具有抑制某个频段内的波传播的特性[3]。带隙特性引入一方面改善了城市轨道交通隔振排桩设计缺乏理论指导的现状，另一方面，通过周期结构或材料的人为设计来调节带隙的带宽和分布，可更具针对性地阻隔目标频段振动，具有良好的应用前景。

周期性隔振桩带隙特性的研究才刚刚起步，目前还是以理论研究为主。黄建坤[3]以圆截面排桩为例，针对周期常数、土体弹性模量和桩半径等各类因素对圆截面排桩带隙起止频率、带宽的影响展开研究，并获得其规律；刘心男等[4]针对采用平面应变模型求解无限周期排桩带隙问题中桩长无限长的假设，建立了三维有限元模型，讨论三维模型与二维模型计算结果的差异，发现随着桩长的增加，二者的结果差异逐步减小，这也说明了在有限周期和有限桩长条件下，带隙范围内的振动可有效衰减，可实现相当的隔振效果；蒲兴波等[5]提出了一种全新方法，用于获取二维周期桩隔振系统的面波频散曲线；此外，甘莹莹[6]针对复阻尼周期排桩的减振性能展开研究，孟庆娟等[7]针对饱和土条件下隔振排桩的衰减特性展开研究。文献[8]利用原理性试验获得了周期结构带隙理论指导下设计排桩的振动传输衰减规律，并与带隙计算结果对比，吻合情况良好，验证了该理论的正确性；姜博龙等[9-10]建立了隧道-地层-隔振周期排桩耦合的三维有限元数值模型，获得了计算带隙范围内隔振排桩的衰减效果，验证了周期结构带隙理论指导下设计排桩隔离轨道交通环境振动的可行性和有效性；提出了基于带隙性能评价函数的选型方法，为隔振周期排桩选型和设计提供依据，提高了选型设计效率。此外，Kattis、冯桂帅等[11-12]研究了隔离桩截面形状对隔振效果的影响，Takemiya 等[13]研究了蜂窝形波阻块（WIB）的隔振效果，而这些构型因素对于带隙特性的影响尚不明确。为进一步丰富该问题的研究，本文提出了带隙特性丰富的三种周期性隔振桩，并对带隙特性的构型影响因素展开研究，为该类型排桩应用及设计选型提供理论依据。本文研究的带隙特性全部为首阶完全带隙，其在隔振应用中有重要意义。

1 周期排桩频散计算的平面波展开法

平面波展开法[2]可用于求解周期排桩带隙特性，其基本假设包括无限周期假设和无限桩长假设，此时振动在排桩-土层中的传播可视为平面应变问题，并解耦为平面内问题和出平面问题。不失一般性，波动方程可表示为式（1）的形式：

式中：ρ 为密度；λ 和μ 为拉梅常数；u 为位移矢量；uj表示位移分量。

其中：

由于排桩的周期性排列，密度ρ和拉梅常数λ和μ可按照傅里叶级数展开为

式中：G1为倒格矢；r为位置矢量。

其中：

f=ρ(r)，λ(r)或μ(r)

r=(x,y,z)

根据Bloch-Floquet理论，位移解可展开为

式中：K为波矢；G2为倒格矢；ω为角频率；u(r,t)为位移矢量。

把方程（2）和方程（3）代入方程(1)，可得到本征方程：

其中：

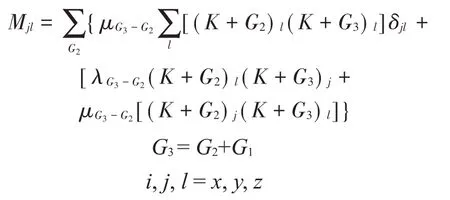
对于散射型排桩，傅里叶系数可表示为

其中：

式中：η 为单个基本单元中桩的占比；P(G1)为结构函数；S 为典型单元面积；J1为第一类第1 阶贝塞尔函数。

使波矢K 扫掠第一不可约Brillouin 区[2]即得到排桩-土体体系的频散曲线和带隙。该方法的正确性和有效性已经过实验验证[14]。

2 蜂窝截面隔振桩构型影响因素研究

蜂窝截面隔振桩首阶完全带隙主要受填充率和周期常数两个构型因素影响。本节以六角晶格排列形式为例，如图1（a）所示，简化的基本单元和计算用到的六角晶格第一不可约Brillouin区分别见图1（b）和图1（c），其中A为散射体（蜂窝截面桩），B为基体（土体），计算所采用的参数如下：土体密度1 900 kg/m3，弹性模量65 MPa，泊松比0.35；混凝土排桩密度2 300 kg/m3，弹性模量30 000 MPa，泊松比0.18。本节计算蜂窝截面隔振桩所采用的几何参数如表1所示。

开展频散关系计算，并画出频散曲线获得其带隙分布。研究其几何构型，包括周期常数和填充率，对其平面内和平面外首阶完全带隙的起始频率、截止频率和带宽的影响规律。其中填充率η可表示为η=基本单元中散射体所占面积/基本单元面积，在本例中，η=(b/a)2。

图2给出了平面内和平面外首阶完全带隙的起、止频率以及对应的带宽随周期常数变化的规律，其中阴影部分表示带宽，余同。

由图2可知，无论是平面内还是平面外，在填充率不变的情况下，首阶完全带隙的起、止频率和带宽都随着周期常数的变大而降低，且平面外的带宽比平面内带宽更大。因此，若设计带隙需具有较宽的带宽，则需要缩小周期常数；若设计带隙需要出现在较低频段，则需要增大周期常数。

图1 蜂窝截面隔振桩平面构型示意图

表1 蜂窝截面隔振桩构型影响因素计算工况

图2 周期常数对蜂窝截面隔振桩首阶完全带隙的影响

图3 填充率对蜂窝截面隔振桩首阶完全带隙的影响

图3给出了平面内和平面外首阶完全带隙的起、止频率以及对应的带宽随填充率变化的规律。由图可知，无论是平面内还是平面外，在周期常数一定的情况下，首阶完全带隙的起、止频率以及对应的带宽都随着填充率的降低而减小，起始频率随填充率增加而变大的速度较缓慢，截止频率和带宽在填充率达到50%以上时，随填充率增加速度变快；同样平面外带隙宽度较平面内更大。从这里可以看出，通过增大蜂窝桩的截面尺寸可有效增加其填充率，对获得低频且具有较宽的首阶完全带隙具有良好的效果。

3 正交截面隔振桩构型影响因素研究

对正交截面隔振桩进行研究，排桩截面形式是正交十字型，以正方晶格排列形式为例，如图4（a）所示，简化的基本单元和正方晶格第一不可约Brillouin区分别见图4（b）和图4（c），其中A为散射体（正交截面桩），B 为基体（土体），材料类型和参数同蜂窝截面隔振桩，图4（c）中字母X、M、Γ为第一不可约Brillouin区顶点，余同。由图4（b）不难看出，正交截面隔振桩具有m、n两个控制尺寸，几何参数更加丰富。本节计算正交截面隔振桩所采用的几何参数参见表2。

根据上述几何参数和材料参数，对以正方晶格排列的正交截面隔振桩结构进行频散关系计算，并画出频散曲线获得其带隙分布情况。研究其几何构型，包括周期常数、填充率和控制参数m、n，对其平面内和平面外首阶完全带隙的起、止频率和带宽的影响规律。其中填充率η可表示为η=基本单元中散射体面积/基本单元面积，在本例中，η=(2mn-m2)/a2。

图4 正交截面隔振桩平面构型示意图

表2 正交截面隔振桩构型影响因素计算工况

图5给出了平面内和平面外首阶完全带隙的起、止频率以及对应的带宽随周期常数变化的规律。可以看出，无论是平面内还是平面外，在填充率不变的情况下，首阶完全带隙的起、止频率和带宽都随着周期常数的变大而降低，且平面外的带宽比平面内带宽更大，这与蜂窝截面隔振桩规律相一致。

图6给出了平面内和平面外首阶完全带隙的起、止频率以及对应的带宽随填充率变化的规律。可以看出无论是平面内还是平面外，在周期常数不变的情况下，首阶完全带隙的起、止频率和带宽随着填充率的变化波动十分大。在低填充率和高填充率两个极端值附近出现了较宽的带隙分布，且平面外带隙在这两种填充率附近分布频段也较低，平面内首阶完全带隙不具备明显规律，从这里可以看出，由填充率作为变量来研究正交截面隔振桩带隙是不合理的，因此，要进一步研究其首阶完全带隙随着几何控制参数m、n的变化规律。

图7给出了平面内和平面外首阶完全带隙的起、止频率以及对应的带宽随控制参数m变化的规律。当周期常数一定时，平面内，随着m/a增大（由于a不变，即m增大），起始频率变化不大，截止频率和带宽先增大后减小，当m/a达到0.8附近时截止频率和带宽最大；平面外，随着m/a增大，起始频率、截止频率先减小后增大，带宽先增大后减小，起、止频率在m/a=0.8 附近达到最小值，带宽在此处达到最大值。

图8给出了平面内和平面外首阶完全带隙的起、止频率以及对应的带宽随控制参数n变化的规律。当周期常数一定时，平面内，随着n/a增大（由于a不变，即n增大），起、止频率和带宽都增大，且当n/a超过0.85时增速变大；平面外，随着n/a增大，起始频率、截止频率减小，带宽增大，但是变化幅度均不如平面内大。

上述分析再次印证了当周期常数和晶格类型确定时，填充率受到两个控制参数m、n共同影响，因此，仅仅从填充率来探寻正交截面隔振桩的首阶完全带隙分布规律是不合理的。

4 X截面隔振桩构型影响因素研究

本节对X截面隔振桩进行研究，X截面隔振桩排布形式如图9（a）所示，晶格类型选取六角晶格，图9（b）、图9（c）为简化的基本单元和六角晶格第一不可约Brillouin区，其中A为散射体（排桩），B为基体（土体）。从图9（b）中不难看出，相比于正交截面隔振桩，X截面隔振桩又增加了一个几何参数，夹角α，因此，具有更加复杂的调节规律。本节计算所采用的几何参数参见表3，材料参数同蜂窝截面隔振桩。

图5 周期常数对正交截面隔振桩首阶完全带隙的影响

图6 填充率对正交截面隔振桩首阶完全带隙的影响

图7 参数m对正交截面隔振桩首阶完全带隙的影响

图8 参数n对正交截面隔振桩首阶完全带隙的影响

图9 X截面隔振桩平面构型示意图

根据上述几何参数和材料参数对以六角晶格排列的X截面隔振桩结构进行频散关系计算并画出频散曲线获得其带隙分布情况，来研究其几何构型，包括周期常数、填充率和控制参数p、q、α，对其平面内和平面外首阶完全带隙的起、止频率和带宽的影响效果进行分析，具体见图10。在本例中，填充率η可由式（6）计算得到。

图10给出了平面内和平面外首阶完全带隙的起、止频率以及对应的带宽随周期常数变化的规律。由图可知，无论是平面内还是平面外，在填充率不变的情况下，首阶完全带隙的起、止频率和带宽都随着周期常数的变大而降低，且平面外的带宽比平面内带宽更大，这与蜂窝截面隔振桩和正交截面隔振桩的规律相一致。

图11给出了平面内和平面外首阶完全带隙的起、止频率以及对应的带宽随填充率变化的规律。平面内，首阶完全带隙整体随着填充率增大而增大，但是在25%～30%之间出现了一个明显的突变，起止频率突然变大、带宽突然变小，这个规律在平面外首阶完全带隙变化规律也有所体现，这主要是因为周期常数一定时，填充率大小同时受到控制尺寸p、q、α三个参数的影响，且起、止频率对于三个参数变化的敏感性差异较大，因此，单独讨论填充率对带隙分布的影响是不合理的，下面将分别讨论带隙分布随参数p、q、α单独变化规律。

表3 X截面隔振桩构型影响因素计算工况

图10 周期常数对X截面隔振桩首阶完全带隙的影响

图11 填充率对X截面隔振桩首阶完全带隙的影响

图12给出了平面内和平面外首阶完全带隙的起、止频率以及对应的带宽随控制参数p变化的规律。当周期常数一定时，平面内，随着p/a增大（由于a不变，即p增大），起始频率、截止频率和带宽都增大，变化幅度不大；平面外，随着p/a增大，起始频率略增加，变化幅度不大，截止频率和带宽增幅较大。

图13给出了平面内和平面外首阶完全带隙的起、止频率以及对应的带宽随控制参数q变化的规律。当周期常数一定时，平面内，随着q/a增大（由于a不变，即q增大），起始频率、截止频率都增大，且当q/a超过0.55 时增速变大，带宽变化幅度不大；平面外，随着q/a增大，起始频率、截止频率和带宽都增大，但是变化幅度不大。

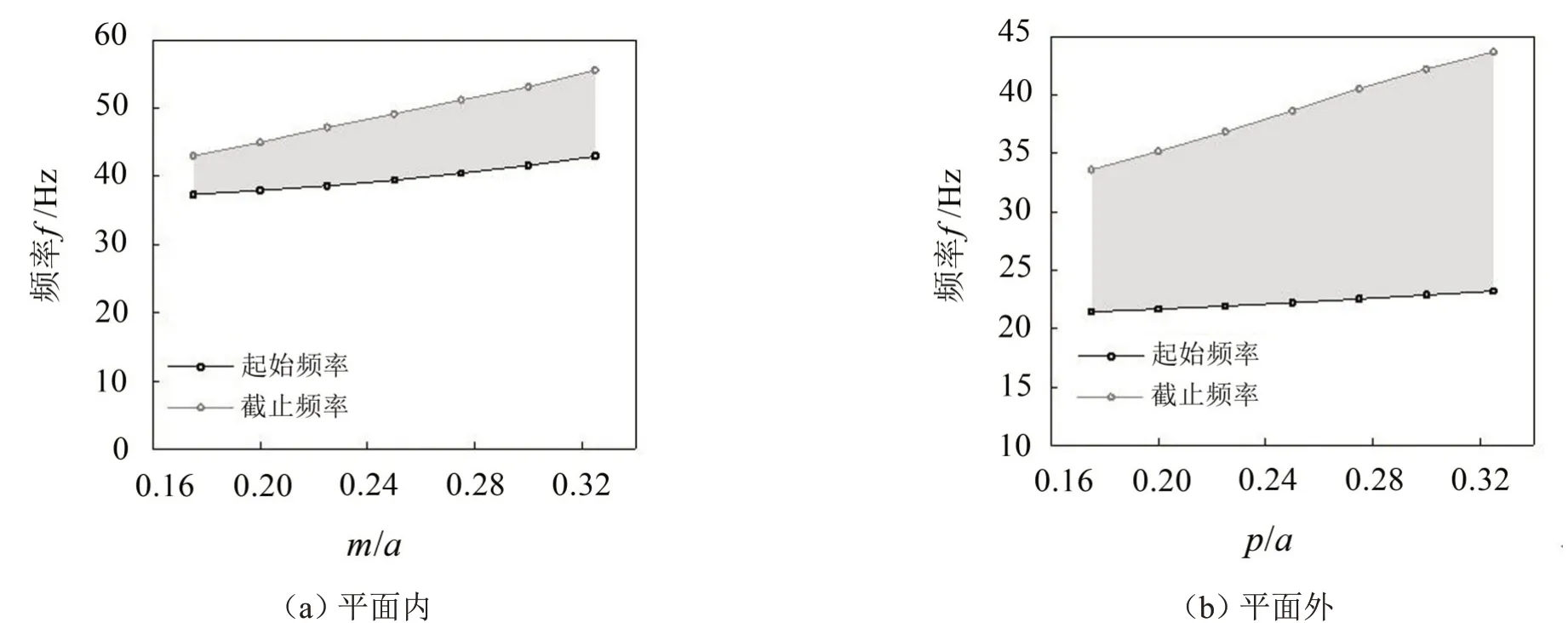
图12 参数p对X截面隔振桩首阶完全带隙的影响

图13 参数q对X截面隔振桩首阶完全带隙的影响

图14 夹角α对X截面隔振桩首阶完全带隙的影响

图14给出了平面内和平面外首阶完全带隙的起、止频率以及对应的带宽随控制参数夹角α变化的规律。平面内，当夹角超过75°时带隙起止频率变大，但对带宽影响不大；平面外，夹角达到75°以上时，带宽急剧下降。可见夹角对平面内带隙起、止频率影响较大，对平面外带宽影响较大。

5 结语

本文提出了三种全新构型的排桩形式，包括蜂窝截面隔振桩、正交截面隔振桩和X截面隔振桩，并根据带隙分析理论对三种排桩进行了频散计算，掌握了其带隙分布特征，揭示了几何构型因素对带隙分布及变化的影响规律。研究发现：

（1）随着周期常数的增加，三种排桩的平面内和平面外首阶带隙的起始频率、截止频率、带宽都呈下降趋势，且平面外的带宽比平面内带宽更大；

（2）随着填充率的增加，蜂窝截面隔振桩平面内、外首阶完全带隙的截止频率和带宽都呈上升趋势，且在填充率达到50%以上时上升变快，起始频率增幅较平缓；

（3）填充率变化对正交截面隔振桩和X截面隔振桩平面内、外首阶带隙分布影响规律不明显；

（4）正交截面隔振桩和X截面隔振桩的几何控制尺寸更复杂、带隙调节能力更丰富。