基于SCADA数据和改进BP神经网络的塔筒应力预测

薛 磊，王灵梅，孟恩隆，郭 超

(1.山西大学 山西省风电机组监测与诊断工程技术研究中心，太原030013；2.山西乾盛新能源有限公司，太原030032)

大型风力发电机本身整体结构复杂，大多分布于地形复杂的山地风电场，不可避免地承受着湍流运动、风切变、塔影效应、尾流效应等作用，而且常在低温、风沙、结冰等恶劣的外部环境下运行，因此存在着系统载荷和振动波动大、故障率高、可靠性差、运维难度大且成本高[1]等问题。此外，风速在时空两个维度都存在着多变性和不平稳性，大型风电机组的机械结构时刻承受着随机交变载荷[2]。塔筒作为其关键支撑结构，一旦发生疲劳损伤或故障，将会导致倒塔等严重事故，造成不可估量的经济损失。因此，对风电机组塔筒的受力情况进行监测评估，具有十分重要的意义。

粘贴应变片是一种常用的载荷测量和监测手段，但这会耗费一定的人力物力和财力。实践中该方法也暴露出一些缺陷，如：输出电压信号容易受到电磁干扰；测量线路较为复杂；此外，最重要的一点是应变片的自身寿命有限，并不适合长期监测。研究出一种经济可靠的风电机组载荷预测方法，是很有必要的。国外的Woo等[3]提出了一种基于多任务学习卷积LSTM(Long short-term memory)模型的风电载荷预测方法。仿真研究结果表明，该模型考虑了输入风流中复杂的湍流结构，能够利用单个深度神经网络模型准确地预测风电机组的功率和结构载荷。 Vera - Tudela 等[4]结合SCADA(Supervisory control and data acquisition)系统的数据，定义了四种滤波器和一维约简算法，选择最优的预测子集并借助于前馈神经网络算法，实现了叶片在平面外弯矩的损伤等效载荷监测。周士栋等[5]基于某2.5 MW风电机组的实测载荷数据和SCADA 系统的多个参数，运用BP(Back propagation)神经网络建立了载荷与SCADA参数之间的关系模型，实现了对7处关键位置的载荷预测。

综上所述，相关研究均建立了神经网络模型，并实现了较好的载荷预测效果。但是BP 神经网络存在着学习收敛速度较慢、不能保证收敛到全局最小点等缺陷[6]。此外，风电机组状态监测参数种类繁多，并伴随着一定的电磁干扰，需要对神经网络输入参量筛选方法做进一步选择。因此，本文采用综合相关系数筛选模型的输入变量，并基于遗传算法和粒子群算法对BP 神经网络模型进行改进。在此基础上，建立GA - BP（Genetic algorithms - back propagation）和PSO-BP（Particle swarm optimizationback propagation）神经网络模型，对钢制塔筒结构进行应力预测。最后，对两种改进模型和BP神经网络模型的预测效果进行比较。

本文以山西某风电场的1.5 MW 陆上风电机组的塔筒应力数据和SCADA 数据为基础，建立基于GA-BP 和PSO-BP 神经网络的塔筒应力预测模型。仿真分析结果表明，在提出的改进模型中，塔筒应力预测精度均得到有效提高，且GA-BP神经网络相对PSO-BP神经网络的预测模型精度更高。

1 基于SCADA 数据的塔筒应力预测模型

基于SCADA 数据和塔筒应力监测数据，利用GA-BP神经网络和PSO-BP神经网络构建的风电机组塔筒应力预测模型结构如图1所示。

1.1 输入数据

输入数据包括SCADA 数据和塔筒应力监测数据两大类。SCADA 数据通过风电机组控制系统收集得到，而塔筒应力监测数据是由塔筒应力监测系统采集得到的，该系统由山西省风电机组监测与诊断工程技术研究中心设计安装[7]。

1.2 数据清洗

风电机组服役期间每一天内都会伴随着工况的变化，由于正常发电工况所占时间较多，且是我们最为关注的工况，因此选择风电机组正常发电工况的数据进行预测。

为确保数据准确有效，对正常发电工况下采集的数据进行清洗。主要清洗的数据有三种：限功率状态下的数据；信息不完整的数据；其他异常数据[1]。

1.3 BP神经网络及改进

BP神经网络按照误差反向传播算法训练，采用梯度下降法来调整各层神经元的权值和阈值，直至最终满足预先设定的误差要求。尽管BP 神经网络有强大的非线性映射、自学习、结构简单等优点，但其也有训练速度较慢、存在陷入局部极小值的可能等不足，因此我们采用进化算法可以对BP神经网络进行改进以提升性能[8]。

图1 塔筒应力预测模型结构图

遗传算法是一类参考自然遗传机制的模拟随机全局搜索和优化方法。遗传算法优化BP 神经网络能获得更好的初始神经网络权值和阈值，网络训练能避免局部最小，同时加快了收敛速度。

粒子群算法是一种群体智能优化算法。借用粒子群算法可以对BP 神经网络的初始权值和阈值进行系统优化，也能够有效实现BP神经网络的收敛速度和精度的提高。

1.4 模型的训练及预测

清洗数据之后，对SCADA 数据中的多个参量与塔筒应力数据进行相关性分析，就可以准确筛选得到与应力变化关系密切的几个SCADA 数据参量。基于这些实测数据，通过GA-BP 神经网络和PSO-BP 神经网络建立塔筒应力与SCADA 数据的关系模型，利用建立好的关系模型进行基于SCADA数据的塔筒应力预测，并对比3个模型的预测效果。

2 风电机组塔筒应力监测

2.1 塔筒应力监测系统

为弥补风电机组载荷监测方面的不足，山西省风电机组状态监测与诊断工程技术研究中心在山西某风电场的1.5 MW 风电机组上安装了塔筒应力监测系统[7]。该风电机组为水平轴双馈型风电机组，主要参数为：轮毂高度80 m，风轮直径82 m，额定风速11.3 m/s。塔筒为圆锥管状钢塔，共分为4 大段，总高度为67 m，塔筒材料为Q345D和Q345E。塔筒应力监测系统共监测了3个不同高度处塔筒的应力情况。该系统由数据采集设备与应变片等组成，通过数据传输，在风电场集中控制中心里即可实现对塔筒应力的监测与掌握。最下层的法兰圈附近布置了9个通道，其中8个应变通道（1-1、1-2、1-3、…、1-8），1个补偿通道；紧接着的法兰圈附近布置了4个通道（2-1、2-2、2-3、2-4）；最上层的法兰圈附近布置了9个通道（2-5、2-6、2-7、…、2-12），其中1个为补偿通道，其余为应变通道。测点示意图如图2所示。塔筒应力监测系统界面如图3所示。图4为现场布置的某个应变片。

塔筒受力类似于头部受载的悬臂梁，从顶部到根部载荷逐渐增大。因此，综合考虑信号质量等因素，本文选择1处布置点的8号应变片所测位置的塔筒应力值，用于预测模型输出层1 个神经元的训练和预测，下文的塔筒应力均指的是此处的塔筒应力。

图2 应力测点示意图

2.2 数据简介

收集的SCADA 信号包括：风速，风向，偏航角度，叶轮转速，有功功率，无功功率，电机转速，电机扭矩，振动X轴，振动Y轴，系统压力等。

塔筒应力数据由应变片测量应变值并得到的。应变片测量的原理是，应变数值乘以材料的弹性模量，即为应力数值。Q345D的弹性模量E为2.1×1011N/m2。则塔筒应力σ可由以下公式计算得到：

上式中：ε为应变片测得的应变值，με。

3 应力预测模型的建立与应用

基于现场实测数据，分别建立基于GA-BP神经网络和PSO-BP神经网络的塔筒应力预测模型。通过两种预测模型的预测结果与实测结果对比，验证优化后的GA-BP神经网络和PSO-BP神经网络的塔筒应力预测模型的有效性及适用性。

3.1 数据库

本研究选择2017年4月19日的测量数据。塔筒应力预测模型使用的数据为间隔30 s 的SCADA数据和塔筒应力测量数据。如前文所述，在原始数据中剔除以下数据：

①启停机等瞬态工况下的数据；

②限功率及未并网发电的数据；

③电磁干扰导致的异常数据；

④不完整的数据[5]。

图3 塔筒应力监测系统界面

异常数据可结合SCADA 中风速、有功功率、叶轮转速、日发电量等信号进行分辨，图5为风速-有功功率-叶轮转速三维散点图，表1为异常数据分类方法的描述。

表1 异常数据的分类

图4 现场布置的应变片

3.2 GA-BP神经网络

采用遗传算法进行优化BP 神经网络的初始阈值与连接权值，主要内容包含BP神经网络结构参数确定、GA-BP和预测输出三个步骤，其主要训练流程如图6所示。

GA-BP 神经网络的对象是初始权值和阈值，其优化过程的步骤如下。

图5 风速-有功功率-叶轮转速三维散点图

图6 GA-BP神经网络模型训练流程

种群初始化。个体编码采用二进制编码，对于每个个体，其均为二进制串，由BP 神经网络输入层与隐含层连接权值、隐含层阈值、隐含层与输出层连接权值、输出层阈值组成。

适应度函数。通过个体可确定BP 神经网络的初始阈值与权值，对训练完成的BP神经网络预测值与期望值之差进行求和，能够得到个体的适应度：

在上式中：n为神经网络输出变量节点的个数；yi和oi分别表示神经网络第i个节点的期望输出和实测输出；k为系数。

选择操作。利用轮盘赌法进行遗传算法选择操作，采用适应度比例选策略，个体i的选择概率pi为

上式中：Fi为个体i的适应度值；k为系数；n为种群数目。

交叉操作。个体基于二进制编码，交叉操作基于实数交叉策略，第k个染色体al与第l个染色体ak在j位的操作分别为

上式中：b为[0,1]间的随机数。

变异操作。选取第i个个体aij的基因进行变异，变异操作方法为

上式中：amax和amin分别为基因aij的上、下界；f(g)=r2(1-g/Gmax)2；r2为随机数；g代表的是当前迭代次数；Gmax表示的是最大的迭代次数；r为[0,1]间的随机数。

3.3 PSO-BP神经网络

采用粒子群算法优化BP 神经网络的初始阈值与连接权值，主要包含三个步骤：BP 神经网络结构参数确定、PSO-BP 和预测输出，训练流程如图7所示。

PSO-BP神经网络的对象是初始权值和阈值，其优化过程的步骤如下。

（1）确定粒子的适应度。通过采集与预测相关的数据和PSO算法处理得到的数据来确定粒子的适应度数值，如下式所示：

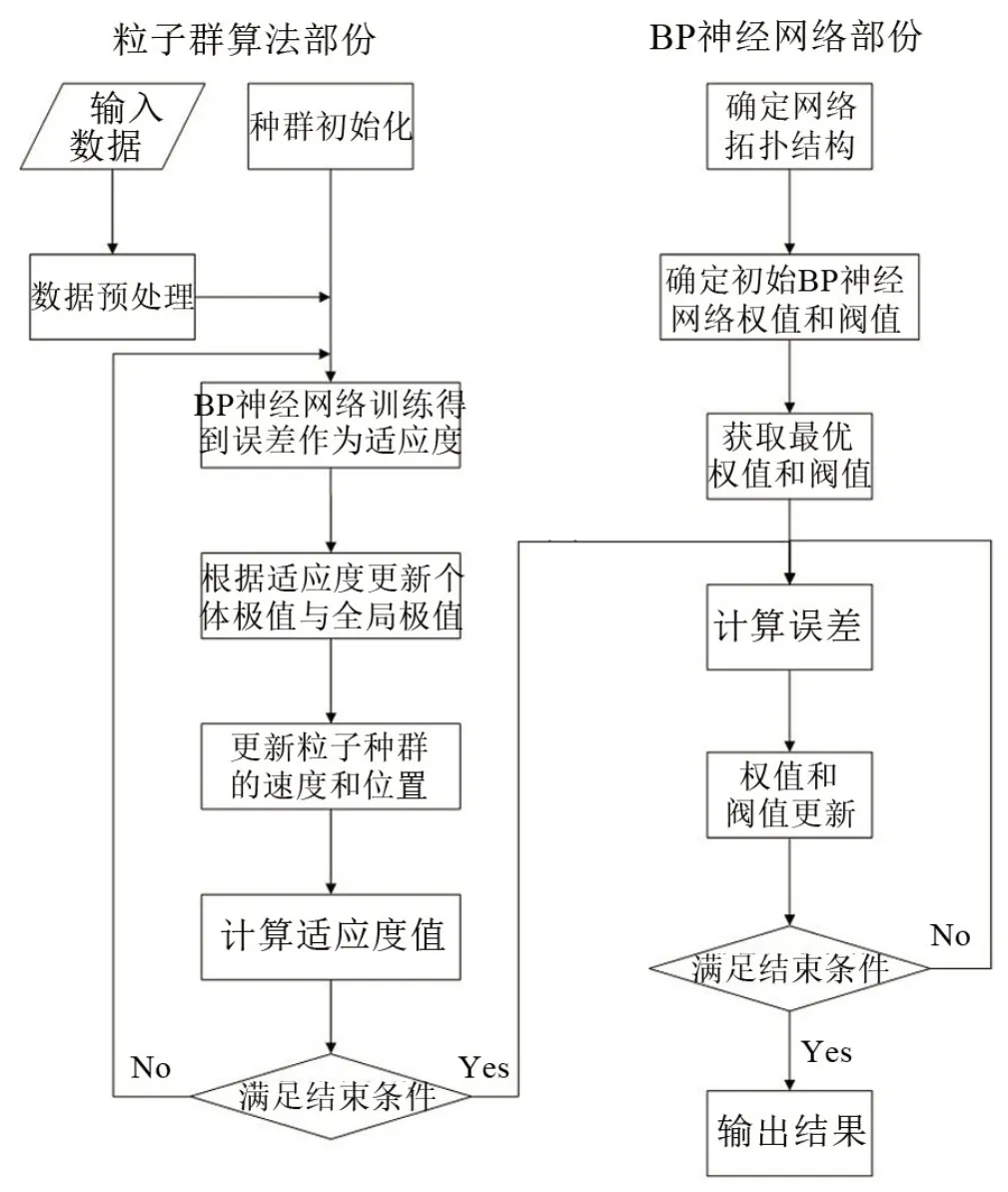
图7 PSO-BP神经网络模型训练流程

其中：N为样本个数，yi为样本i的观测值为样本i的预测值。

（2）粒子适应度的选取。选取当前粒子适应度Psee和历史最优适应度Rbest中最优的，用来作为当前粒子的适应度；选取当前粒子的历史最优适应度和全局最优适应度gbest中最好的，作为当前粒子的历史最优适应度。

（3）对粒子的位置及速度进行更新。相应的计算公式如下：

在上式中：a=1,2,…,n；b=1,2,…,n,l1为粒子个体最优步长，l2为粒子的群体最优步长，r1和r2为之间的随机数，Xab表示第a个粒子的位置，Vab表示第a个粒子的速度。

（4）设置粒子速度最大区间为[0,Vmax]，当粒子的速度大于Vmax，则该粒子此时的速度改为Vmax。

（5）对当前迭代次数与最大迭代次数作比较。如果CurIte≥MaxTte，则停止迭代；否则，返回步骤①确定粒子的适应度。

3.4 参量选择

风电机组各个子系统或部件之间存在复杂的耦合关系，而训练参数的选择对于神经网络模型的准确性具有重要意义。因此为尽量减小采集数据样本中非线性畸变或脉冲干扰、风机的运行波动、电网负荷的随机性等多种因素的干扰，以及准确建立风电机组塔筒应力与SCADA 数据之间的关系模型，引入Pearson、Kendall、Spearman 相关系数的综合相关系数来分析变量间的关系，以优化参量选择[1]。

（1）Pearson相关系数

设(X,Y)(i=1,2,…,n)是来自连续监测变量(X,Y)的样本，则Pearson相关系数为

式（10）中：rp是Pearson相关系数；Xˉ和Yˉ分别代表了X和Y样本的平均值；n是样本的总体个数。Pearson的值rp反映了X和Y的相关性，rp越接近于1 或者-1，X和Y的相关性越显著，当rp越靠近于0，表明变量X和Y之间越不相关。

（2）Kendall秩相关系数

设(x1,y1)、(x2,y2)分别是两个连续监测变量的样本值，则样本数为n产生的对数为C2n=n(n-1)/2，Nc表示协同数对的个数，可由(x1-x2)(y1-y2)＞0 来计算，Nd表示协同的数目对，可由(x1-x2)(y1-y2)＜0 来计算，并且有Nc+Nd=n(n-1)/2，由Kendall的相关性定义：

当Kendall的值rk越接近于1 或者-1，两个主要变量的相关性越强，rk越接近于0，两个监测变量就越不相关。

（3）Spearamn相关系数

对于两个监测变量参数Xi和Yi，分别求得其两个变量参数的秩记为Pi和Qi。则由Spearman 相关系数定义：

当Spearman 的值rs越接近于1 或者-1，两个变量的相关性越显著，rs越接近于0，X和Y越不相关。对收集的SCADA 信号和塔筒应力数据等参量进行相关性分析，可以从中剔除无关或关系较弱的冗余参数，从而提高模型计算速度与精度。本文采用基于Pearson、Kendall、Spearman 三种相关系数的综合相关系数r来进行参量选择。综合相关系数r的计算公式如下：

根据相关系数法理论，当两个物理量之间的相关系数绝对值满足0 ≤ |r|≤0.09 时，表示两个监测变量之间没有相关性；当相关系数绝对值满足0.09 ＜ |r|≤0.3 时，可认为两者存在弱相关性；当相关系数绝对值满足0.3 ＜ |r|≤0.5 时，表明两者具有中等相关性；当相关系数满足0.5 ＜ |r|≤1 时，足以说明两者之间是强烈相关的。因此，本文从众多的SCADA参量中筛选出综合相关系数大于0.5的参量和塔筒应力数据作为输入变量。表2是筛选得到的模型输入参量之间的相关系数（表中相关系数均为绝对值大小）。

表2 塔筒应力与输入参量间的相关性

1 处布置点的塔筒应力主要取决于该截面处的塔筒弯矩大小，而塔筒弯矩主要与塔顶弯矩、塔筒上部所受推力、风在此截面处产生的弯矩和塔筒重力等有关。塔筒弯矩产生及传递的过程为：风-叶片-叶轮-轮毂-传动系统（齿轮箱）-发电机-机舱-塔顶-塔筒。风作用到叶片上，驱使叶轮旋转，旋转的叶轮带动齿轮箱主轴转动并将动能输入到齿轮副，经过变速，齿轮副将动能通过联轴器传递给发电机，发电机将输入的动能转化为电能，最终经过变流器及变压器输送到电网。风速、叶轮转速、桨距角通过轮毂扭矩影响着齿轮箱主轴力矩的大小，齿轮箱输入轴温度、齿轮箱输出轴温度、齿轮箱油温均与主轴力矩息息相关；同时主轴力矩是发电机电机扭矩的来源，影响着电机转速，也间接影响着有功功率、无功功率、变频器功率、变频器无功功率、电流。主轴力矩和其它载荷影响着塔顶弯矩、塔筒上部所受推力，因此，这些输入参量与塔筒应力密切相关。

由于塔筒不同高度截面处所承受的重力不同，所受风速的大小和风向不同，不同应力测点位置的塔筒应力与输入参量间的相关性也不尽相同。同一高度、风速和风向接近的两个位置的塔筒应力与输入参量间的相关性接近。

3.5 模型预测结果对比

对所选的输入变量进行数据信息的处理后，分别针对GA-BP 神经网络模型、PSO-BP 神经网络模型以及BP 神经网络模型进行训练。建立的数据库中共有400 组数据，其中，选取了前320 组数据作为训练数据来建立塔筒应力预测模型，其余80组数据作为测试样本来验证和对比不同模型的准确性。

参照相关研究中对模型准确性的度量，本研究引入了平均相对误差MAPE (Mean absolute percentage error)和均方根误差RMSE(Root mean square error)作为指标[1]，对基于GA-BP 神经网络、PSO-BP神经网络和BP神经网络建立的塔筒应力预测模型进行对比分析。

其中：ym是塔筒应力的测量值，yp为模型预测值，n=1,2,…,N是测试样本的数量，N为80。

设置1 层隐含层，为探究最合适的隐含层神经元个数，分别对比了隐含层神经元个数为4、5、6…、14时，三种不同预测模型预测10次的平均误差，表3列出了隐含层神经元个数为4、5、6、7 时的预测误差。结果表明，隐含层神经元个数为6 时的预测效果最好。

表3 不同隐含层神经元个数的预测误差/（%）

输入层设置为13 个神经元，隐含层为1 层，共6个神经元，输出层设置为1 个神经元。在三种神经网络模型进行训练的过程中，为保证对比和兼顾训练速度，统一设置了最大训练次数为1 000，网络训练目标为0.001，学习率为0.15；在遗传算法优化神经网络初始权值的过程中，种群数量为20，遗传迭代次数为100，交叉概率的值为0.7，变异概率为0.1；在粒子群算法优化神经网络初始权值的过程中，种群数量为20，进化次数为100。通过对基于三种神经网络算法的塔筒应力预测模型分别进行多次仿真训练，分别取80 个预测值的平均值与期望值进行比较。10次预测的效果对比情况如图8和图9所示。

图8 三种神经网络模型预测值与期望值的对比

图9 三种神经网络模型预测的相对误差

通过式（14）和式（15）计算对比三个塔筒应力预测模型的预测效果，结果如表4所示。

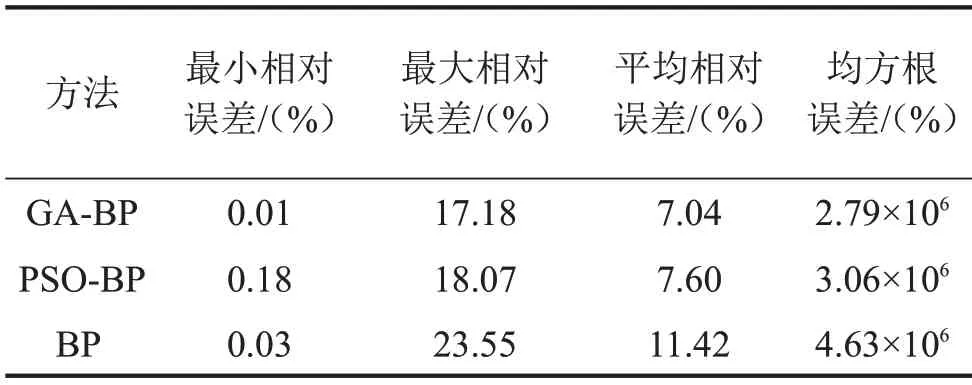
表4 三种神经网络模型预测性能对比

GA-BP神经网络模型仿真预测的最大的相对误差为17.18%，最小的相对误差仅为0.01%，平均相对误差MAPE为7.04%，说明GA-BP神经网络的仿真预测效果好，可以较为准确地预测塔筒应力的变化；PSO-BP神经网络模型仿真预测的最大相对误差为18.07%，最小相对误差为0.18%，平均相对误差MAPE为7.60%，说明PSO-BP神经网络的仿真预测效果较好，可以较好地预测塔筒应力的变化；而BP神经网络的最大相对误差为23.55%，平均相对误差MAPE 为11.42%。GA-BP 神经网络、PSO-BP 神经网络和BP 神经网络模型的均方根误差RMSE 分别为：2.79×106、3.06×106、4.63×106。可以看出，通过对BP神经网络模型进行优化之后，GA-BP神经网络和PSO-BP神经网络模型在预测的最大相对误差、最小相对误差、平均相对误差MAPE 方面都有了明显的优化，均方根误差RMSE 也小于BP 神经网络模型。3 种塔筒应力预测模型中，GA-BP 神经网络模型的预测精度最高。

进一步对比三个模型的预测性能，GA-BP 神经网络模型明显优于BP 神经网络模型，也优于PSOBP神经网络模型，说明采用遗传算法和粒子群算法对BP神经网络进行优化是可行的。

基于GA-BP 神经网络的塔筒应力预测模型具有更强的预测能力，网络输出值与实际值更加接近，预测误差、精度都优于BP神经网络、PSO-BP神经网络模型，是一种更为有效的塔筒应力预测方法，对挖掘风电机组海量监测数据用于机组载荷监测具有一定的应用意义。

4 结语

本文以1.5 MW风电机组塔筒为例，对比了基于BP 神经网络和改进后的GA-BP 神经网络、PSO-BP神经网络的塔筒应力预测模型预测效果，研究结果表明：

(1)针对SCADA 系统信号种类繁多、风电机组状态监测时伴随着不同程度的电磁干扰等因素，基于综合相关系数选取输入参量，可最大程度减少这些因素的干扰，不仅避免了使用试错法的耗时耗力，同时实现了参量选择的准确和高效。

(2)利用改进后的GA-BP 神经网络、PSO-BP 神经网络的塔筒应力预测模型，均能建立更优的预测模型，平均相对误差MAPE 分别为7.04%、7.60%，均小于BP 神经网络相对误差MAPE 的11.42%，其中GA-BP 神经网络的塔筒应力预测模型预测精度最高。说明本文提出的基于GA-BP神经网络、PSOBP 神经网络的塔筒应力预测模型，比基于BP 神经网络的预测模型更有效准确，更适合塔筒应力监测。

(3)基于GA-BP 神经网络、PSO-BP 神经网络的塔筒应力预测模型具有较高的预测精度，对于风电机组其它部位的载荷预测具有借鉴意义。

为进一步实现大型风电机组的载荷预测与评估，未来可从以下方面进行更加深入的研究：

①研究基于风电机组塔筒应力预测模型能否推广到其他关键部位的载荷预测中；

②将应力预测模型应用于塔筒安全监测与预警工作中。