改进的A-FAP图像去噪算法
刘巍巍,李海新
(沈阳工业大学 机械工程学院,辽宁 沈阳 110870)
0 引 言
在处理材料图像时[1],国内外学者提出几种典型的去噪算法,如文献[2]中的巴特沃斯高通滤波去噪,文献[3]中的维纳滤波去噪,文献[4]中的多方向的加权均值滤波去噪以及文献[5]小波变换的图像去噪研究等,以上算法对图像进行了不同程度的去噪,但是这些去噪算法的掩模模板均为整数阶积分,在去噪的同时造成了图像边缘和纹理细节的缺失。
近年来,分数阶微积分在图像去噪上成为一个新的研究热点[6,7]。文献[8,9]采用Grünwald-Letnikov分数阶微积分掩模去噪,虽然可以保留部分纹理细节,但是整幅图像的噪声点未能精确去除;文献[10]提出的分数阶Alexander多项式去噪算法,能较好保留图像的纹理信息,但该算法利用自定的微积分阶次,在处理不同类型的噪声时,只能根据同一阶次的频率特性曲线,难以达到优良的去除噪声效果。
本文提出改进的A-FAP图像去噪算法,通过分析原始图像的灰度值,调定去噪的微积分阶次,利用构造的自适应分数阶Alexander函数(adaptive fractional Alexander polynomials,A-FAP)滤波器对图像进行去噪,使处理后的图像具有清晰的视觉效果,对图像的弱边缘和纹理细节信息的显现具有明显优势。
1 问题描述及算法流程
材料图像在传输过程中受到信号和设备的干扰,极易产生高斯、椒盐和乘性噪声,从而造成图像失真和模糊,图像边缘和纹理细节信息的缺失则会导致色偏现象的出现。本文提出改进的A-FAP去噪算法,通过建立去噪模型,构造A-FAP掩模模板对图像进行去噪,利用小波反变换对图像进行重构,得到去噪后的图像。本文算法的过程如图1所示。
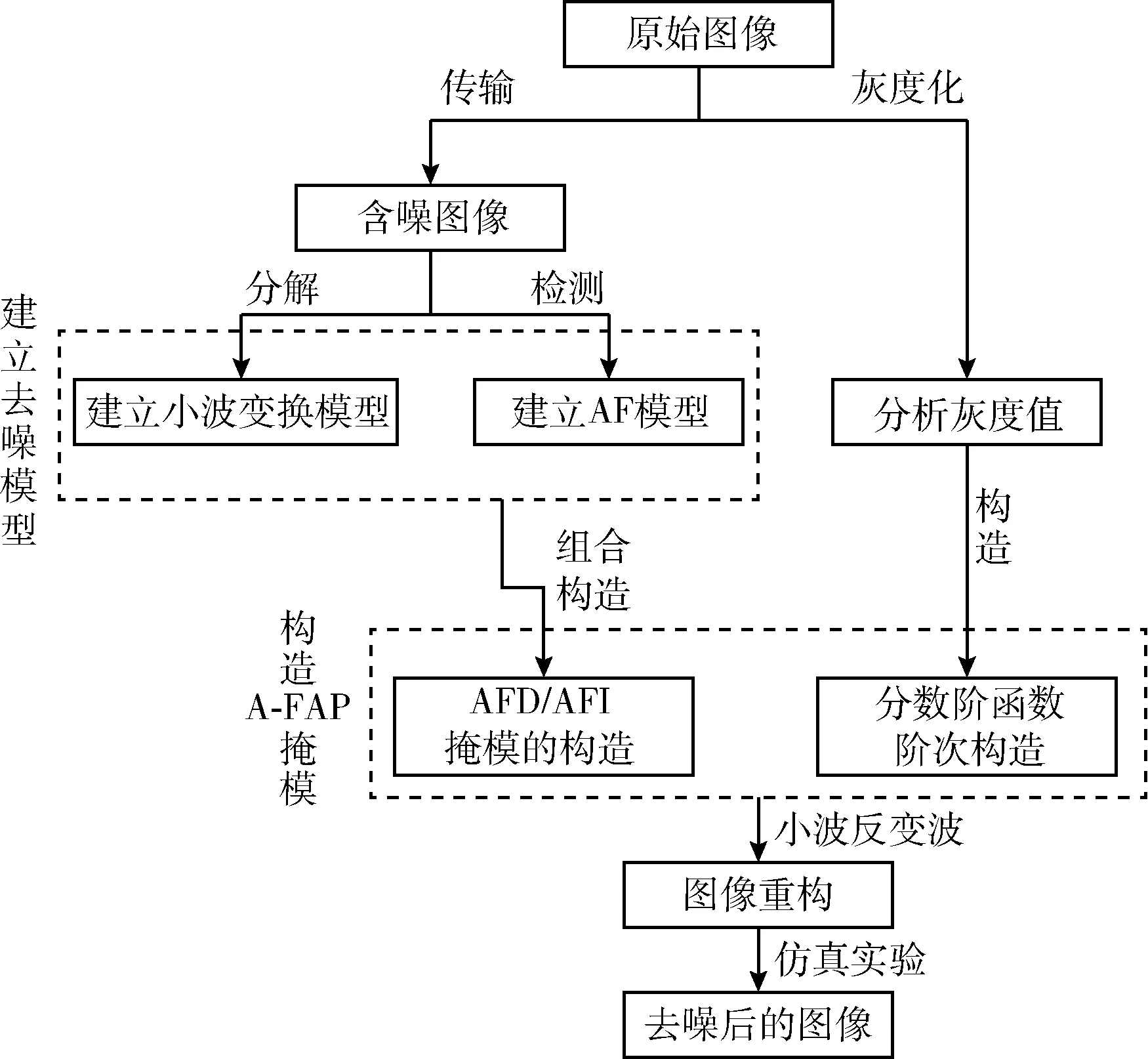
图1 A-FAP算法去噪流程
2 去噪模型的建立
2.1 建立二维离散小波变换模型
小波变换在处理大小为M×N的图像时,通常根据规范正交基函数,将小波级数进行展开,展开为二维尺度空间函数和二维小波空间函数;具体展开形式如下

(1)

(2)

对受到噪声污染的lean图像,采用二维离散小波进行二层展开,如图2所示;其中J2是低频分量,通过分级滤波和沿横纵方向的双重提取获得;H1、H2、V1、V2和D1、D2表示水平、垂直和对角线上的高频分量系数。尺度空间函数二层展开k的近似J2是图像的高尺度、低频分量,小波空间函数中的i的二级分解为H2、V2、D2、H1、V1和D1是低尺度、高频分量。因为噪声属于高频信号,通常存在于高频分量中。

图2 二维离散小波的二级展开
2.2 建立Alexander分数阶微积分(Alexander fractional,AF)模型
2.2.1 Alexander函数

(3)
式中:lm为正整数。
2.2.2 分数阶微积分函数
当v>0时,函数s(t)的分数阶微积分为
(4)

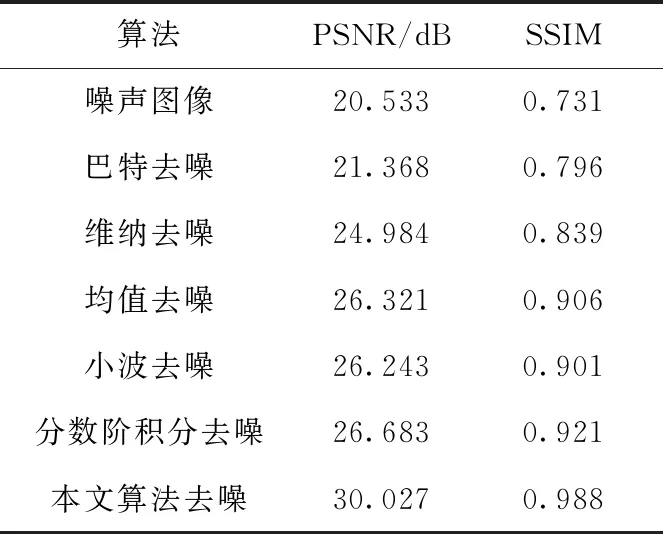
当0 (5) 为保持图像的边缘信息,进一步丰富图像纹理细节,更好抑制噪声,对式(4)、式(5)进一步推导;α=0时 (6) (7) 基于Mittag-Leffler函数的定义参见文献[6],结合Alexander函数(3),根据式(6)、式(7)得出分数阶微分算子(AFD)和分数阶积分算子(AFI)的两个掩模窗口系数。 分数阶微分算子(Alexander fractional differential,AFD) (8) (9) (10) (11) (12) (13) 分数阶积分算子(Alexander fractional integral,AFI) (14) (15) (16) (17) (18) (19) 图3 分数阶掩模模板 图像的边缘和纹理信息主要与图像结构特征(图像梯度)、图像统计信息特征(信息熵)和图像差异特征(对比度)有关,因此利用以上3个特征构造自适应分数阶函数,确定分数阶微分阶次。 图像梯度(G)体现了图像灰度频率特征,判断图像纹理信息是否丰富;图像在灰度点(x,y)处的梯度是对该图像离散小波模型的微分,具体表示为:G[f(x,y)]=[∂f/∂x,∂f/∂y];为计算方便,定义梯度模值为 |G|=max{|Gx|,|Gy|} (20) 信息熵(S)是表征图像灰度信息量的频率变化,S较小时,图像表现为平滑区域,反之,则为边缘和平滑区域。表达式为 (21) 式中:pij表示为灰度点(x,y)在分量展开区域中出现的概率。 对比度(C)表现图像灰度差异性的特征,图像灰度差异性显示图像的清晰度、纹理度,即图像越清晰,纹理细节越明显,C越大,反之,C越小。其公式为 (22) 式中:σ为图像灰度值的标准差,u2为图像灰度的中心距离。 因此,分数阶微积分算子根据以上3个特征参数进行自适应的变化,本文对二维离散小波分解后的图像进行去噪,高噪声密度区域主要集中在高频区域;因微分阶次随G、S、C的增加而增加,所以本文利用指数函数的性质,构造阶数v与f(G,S,C)之间的函数关系。 即 v=ef(|G|,S,C)-b (23) 为突出掩模中心点的纹理细节,增设一个平衡系数β,式中,f(|G|,S,C)=lG+mS+nC+β,表示对梯度、信息熵和对比度的加权求和。其中l+m+n+β=1,l,m,n分别表示为梯度加权系数、信息熵加权系数和对比度加权系数。 对于分数阶阶次函数v=ef(|G|,S,C)-b,设:φ=f(|G|,S,C),即v=eφ-b,φ∈[0,1];对分数阶次函数进行求导,v′=eφ>0,函数在区间[0,1]内>0,函数为增函数,即vmin=1-b,vmax=e-b。 为保证v∈[0,1],b的取值范围为[1,e-1],保持去噪效果的稳定性,本实验b取中间值1.35。 为验证本文算法的去噪性能,选取标准库中受到高斯、椒盐和乘性噪声污染的256×256的原始lena图像,在操作系统为Windows7,处理器为inter-COREi3-3217 CPU,内核为1.80 GHz,RAM2.00的条件下,通过软件MATLAB 2013a进行去噪处理。仿真实验的具体分析过程如下: (1)对受到噪声污染的图像进行二层级数展开,得到高、低频分量系数; (2)对低频分量系数采用AFD模板进行处理,最大限度保留低频图像的边缘和纹理信息; (3)对高频分量系数(水平、垂直、对角)运用构造的分数阶函数自适应确定去噪阶次,采用AFD和AFI掩模模板相结合的方案进行处理,即可以显现高频图像的边缘和纹理信息,又可以最大程度抑制噪声; (4)对处理后的分量系数进行重构,得到去噪后的图像。 对处理后的lena图像,采用PSNR和SSIM对算法进行性能评价。其定义参见文献[12] (24) (25) 式中:Ii,j是像素点为256×256的原始lena图像,Ki,j为去噪后的图像,u1,u2分别为Ii,j,Ki,j的均值,σ1,σ2分别表示Ii,j,Ki,j的方差,σ1,2表示Ii,j,Ki,j的协方差,为保持系统的稳定性,引入定量常数c1=0.01,c2=0.02;其PSNR越高,SSIM越大,表示图像的去噪效果越好。 采用3组实验验证本算法的去噪效果,分别利用巴特去噪、维纳去噪、均值去噪、小波去噪、分数阶积分去噪和A-FAP图像去噪算法对高斯噪声、椒盐噪声、乘性噪声进行去噪。 第一组(图4)对加入高斯噪声(噪声中有均值u1=u2=0,方差σ1=σ2=0.02,协方差σ1,2=0)的lena图像进行去噪效果的验证,并与其它算法进行对照,去噪结果分析如图4所示。 图4 不同算法对受到高斯噪声的处理结果 图4(a)为初始lena图像,图4(b)是加入高斯噪声的图像。图4(c)~图4(f)是对加入高斯噪声的图像,通过传统方法进行去噪[1-5],对高斯噪声的处理有一定的抑制作用,但是易造成lena图像的面部、头发和帽檐边缘部分出现模糊现象。图4(g)为分数阶积分去噪,根据文献[11]利用梯度检测噪声点,运用分数阶积分模板进行去噪,图像的边缘细节得到了部分显现,整体的去噪效果有所欠缺,显现出一种模糊现象。利用本文算法去噪的结果如图4(h)所示,该算法抑制了大量的噪声,保留了图像的边缘和纹理细节,使lena图像的面部、头发和帽檐边缘部分清晰显示出来。 此外,从表1中的PSNR值和SSIM值可以得出,本文算法得到的PSNR值和SSIM值高于其它每个算法,相对于其它算法的平均值提高了2.286 dB、0.123,这从客观说明了本文算法对高斯噪声去噪效果的良好性。 表1 各算法对高斯噪声去噪后的PSNR和SSIM 第二组(图5)对加入椒盐噪声(其噪声概率为0.2,u1=u2=0.01,方差σ1=σ2=0.03,协方差σ1,2=0.01)的lena图像进行去噪效果的验证,并与不同算法进行对比,去噪结果分析如图5所示。 图5 不同算法对受到椒盐噪声的处理结果 图5(a)为原始图像,图5(b)是被椒盐噪声污染的lena图像。图5(c)~图5(f)为传统去噪算法,其中巴特去噪[2]和维纳去噪[3]对噪声的抑制能力较弱,均值去噪[4]和小波去噪[5]对椒盐噪声有一定的抑制作用,但是整幅图像的边缘和纹理细节较为模糊。图5(g)为分数阶积分去噪[12](阶次为v=0.52),图像边缘和细节信息得到了很好的凸显,但是由于缺乏梯度的自适应阶次判别,其噪声点未能很好的去除。本文算法的去噪结果如图5(h)所示,对于图像的纹理细节有较好的保留,对噪声造成的模糊边缘有针对性的去除,从图像的清晰度和视觉感知上较其它算法有了明显的改善。 同理,对比表2中的数值可以得出,本文算法得到的PSNR值和SSIM值高于其它每个去噪算法,相对于其它算法的平均值提高了4.707 dB、0.108,这从客观说明了本文算法对椒盐噪声去噪效果的优越性。 表2 各算法对椒盐噪声去噪后的PSNR和SSIM 第三组(图6)对加入乘性噪声(u1=u2=0,方差σ1=σ2=0.04,协方差σ1,2=0)的lena图像进行去噪效果的验证,并与其它算法进行对照,去噪结果分析如图6所示。 图6 不同算法对受到乘性噪声的处理结果 图6(a)为初始图像,图6(b)为加入乘性噪声的lena图像。图6(c)~图6(f)是采用传统滤波器进行乘性噪声去噪的结果图,其中巴特算法[2]对乘性噪声抑制作用较弱,维纳算法[3]、均值算法[4]和小波算法[5]对乘性噪声有一定的抑制能力,噪声得到了很好的去除,但是对于lena图像面部纹理细节和发丝的边缘细节未能得到较好的保留,造成局部模糊的现象。图6(g)是运用分数阶积分[13]对乘性噪声进行去噪的结果图,由于该算法对乘性噪声点的去噪能力有限,虽然对于发丝的细节有所保留,但是该图整体较为模糊。图6(h)为本文算法去噪,根据图像的灰度情况,自适应的确定积分阶次,抑制了大量的乘性噪声点,并对图像面部、发丝的纹理和边缘细节得到了保留。 通过比对表3中的结果可以得出,本文算法得到的PSNR值和SSIM值高于其它算法,相对于其它算法的平均值提高了2.259 dB、0.070,进一步说明了本文算法对乘性噪声去噪的性能高于其它算法。 表3 各算法对乘性噪声去噪后的PSNR和SSIM 本文提出改进的A-FAP图像去噪算法,通过图像的梯度、信息熵和对比度的参数变化,判断去噪的微分阶次,配合高低频二级展开的分量系数,针对性地抑制大量噪声点,利用构造的AFD、AFI掩模算子,对图像进行自适应去噪。仿真结果表明,本文提出的算法对比与其它各类型的算法,从视觉感知和性能评价上显现出本文算法的去噪效果,其抑制噪声的能力突出,保持图像纹理细节和边缘信息上具有优势,得到的PSNR值和SSIM值高,从而验证了本文算法在对高斯、椒盐和乘性噪声去噪方面的准确性和优越性。3 自适应分数阶Alexander滤波器的构造
3.1 Alexander分数阶微积分掩模的构造

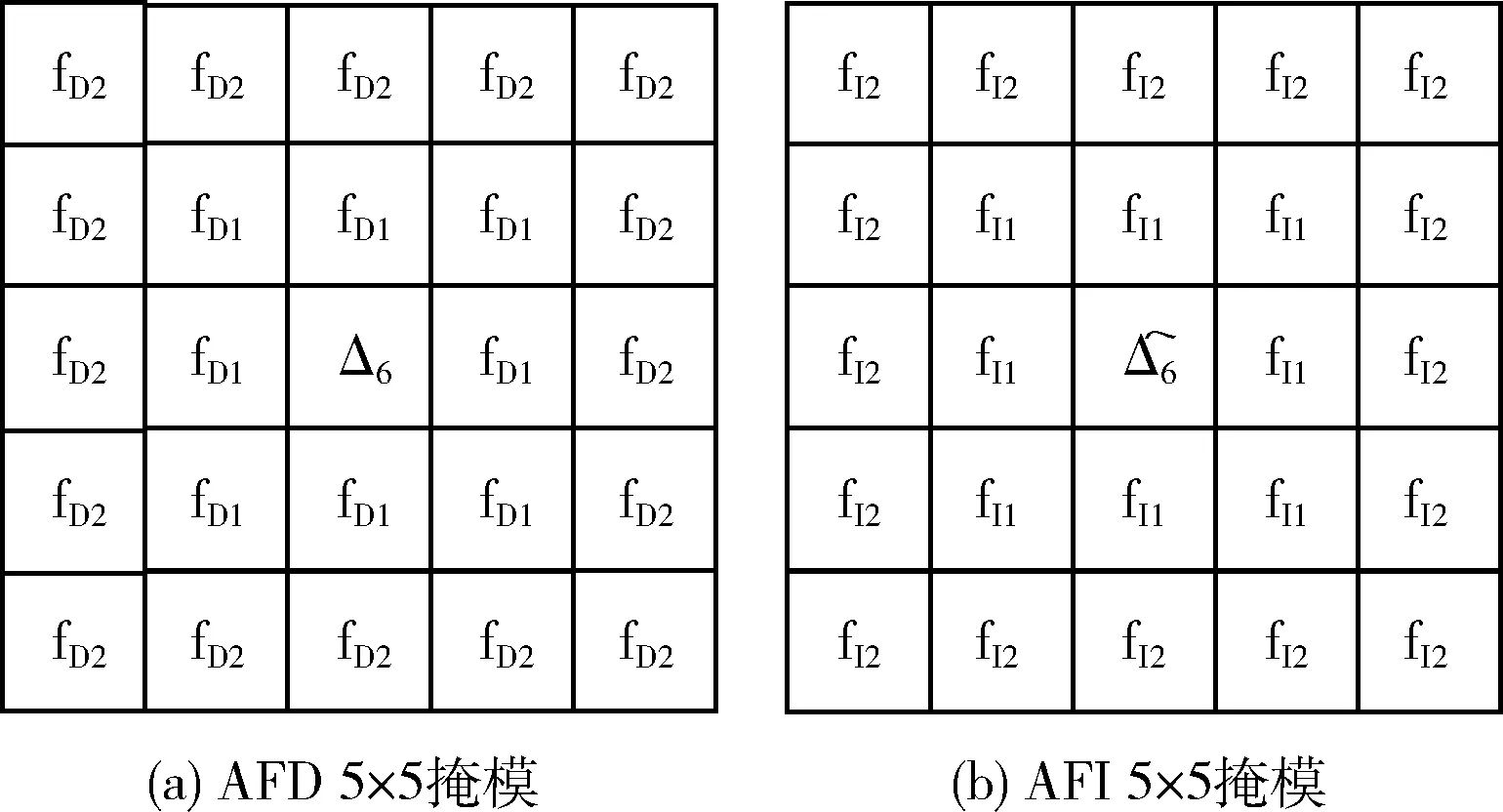
3.2 自适应函数阶次的构造

4 仿真实验及结果分析
4.1 仿真实验
4.2 结果分析





5 结束语

