利用布隆滤波二次拆分的数据倾斜处理算法
张 强,张学文
(1.重庆大学城市科技学院 电气信息学院,重庆 402167;2.北华大学 机械工程学院,吉林 吉林 132013)
0 引 言
大数据处理往往采用MapReduce并行任务处理的方式来进行[1],主要包含映射(Map)操作和归约(Reduce)操作[2]。其中,Reduce操作中混洗(Shuffle)阶段的功能为通过调用分区程序将映射器(Mapper)的输出结果转移到归约器(Reducer)中进行排序(Sort)与归约(Reduce)操作[3]。分区程序往往采用Hash函数,并忽略Mapper与Reducer之间网络拓扑以及Mapper输出数据量规模。缺点在于由于并行计算任务量、数据集物理属性参数分布特性、Mapper数据规模以及网络拓扑分布的差异性,Shuffle的时间开销将变得不可控[4-6],即数据集的倾斜特性将影响Map-Reduce的计算性能。
文献[7]以文件均衡偏差值作为数据倾斜的度量标准,设计了面向数据均衡的贪心策略,但缺点在于抽样统计操作会引入额外的时间开销。文献[8]通过JobTracker监控Map阶段产生的数据规模,提出改进的Hash分区函数将较大数据规模的任务索引到负载较轻的Reducer上。此种方案同样引入额外的时间开销,且降低了Mapper与Reducer的并发度。此外,现有研究仍有以下两个缺点:①现有文献大多以Reducer同构为假设前提设计数据倾斜消除策略,但忽略了Reducer硬件配置、计算资源等差异性对MapReduce性能的影响;②构建Mapper与Reducer最优映射关系为NP难问题[9],需在时间开销与映射方案选择间折中选取。
针对以上不足,提出一种基于流量开销自适应感知和自动学习机的数据倾斜处理算法。主要创新点为:
(1)在Map阶段检测过载Reducer,并考虑到硬件配置、计算资源等异构特性的实际约束,提出二次分拆机制对Mapper输出数据集进行分片,设计了基于布隆滤波的Hash分区算法,使Mapper根据自身流量开销部署到Reducer。与传统算法相比,所提策略能够根据Mapper流量开销自适应选择Reducer的候选范围,缩短Reducer选择的时间开销。
(2)在Reduce阶段设计了基于学习自动机的分区算法,使用均匀分布抽样算法获取任务类型与规模,并以Reducer候选范围为约束条件搜索Mapper与Reducer在有限时间内的近似最优映射关系。与传统方案相比,学习自动机方法有效解决了映射构建时的NP难问题,提升分区算法执行效率。
1 基于布隆滤波Hash分区的流量开销感知机制
Mapper中的输出为具有
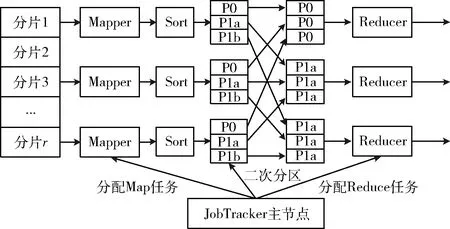
图1 所提改进Hash分区策略
1.1 提前传输与二次拆分机制
为缩短MapReduce计算时间开销,设Mapper执行完成度达到某一阈值后,对于已完成的任务进行提前传输。设θ为Mapper完成任务量占总任务量的百分比,即
(1)
式中:Taskfinished和Task∑分别表示已完成的任务数量以及总的任务数量。符合传输条件的判据为数据量分片值大于分片均值,分片均值计算如下
(2)
式中:Saverage为分片均值,Num为Reducer的总数量。
在Map阶段完成后,主节点统计所有中间结果的数据倾斜程度,并按照式(2)重新计算现阶段的负载均值。对于超过负载均值的数据进行二次拆分,其拆分公式为

(3)

采用式(3)所示拆分操作后,尽管主节点中保留了二次拆分的具体列表,但Mapper端的中间结果中,分片仍然是完成的临时文件。因此,在确定各子分片与Reducer间的对应关系后,临时文件需要整体打包发送至Reducer节点。若所有分片无差别地传输至Reducer势必引发网络负载的激增。因此,设计了布隆滤波器以选择仅符合条件的子分片数据进行传输。
1.2 布隆滤波传输机制
如图2所示,对于每一个子分片,首先创建具有n个特征比特串和k个Hash散列函数的布隆滤波器。传输过程包含如下两个子过程。

图2 二次拆原理
(1)特征置位阶段:初始条件n个特征比特串全为0。进一步地,定义子分片的Key值为每个散列Hash函数的输入,输出则为[0,n-1]之间的整数,从而映射到特征比特串的n个位置。若对应的特征位置为0,则将其置为1;反之,若该位置已经为1,则保持不变。
(2)查询传输阶段:对特征比特串1~n通过Hash函数进行逐次计算,生成对应的k个Hash值,并以此作为布隆滤波阈值。可以严格证明,布隆滤波的错误传输概率P满足如下关系[11]
(4)
式中:Numbit为通过布隆滤波器的特征比特串。
基于上述分析可知,与传统一次分区操作相比,所设计方法实现了对规模过大的数据块的自适应二次拆分,且避免了数据块重复传输带来的额外网络开销。
2 基于学习自动机的Mapper-Reducer最优映射机制
2.1 变动作学习自动机基本原理
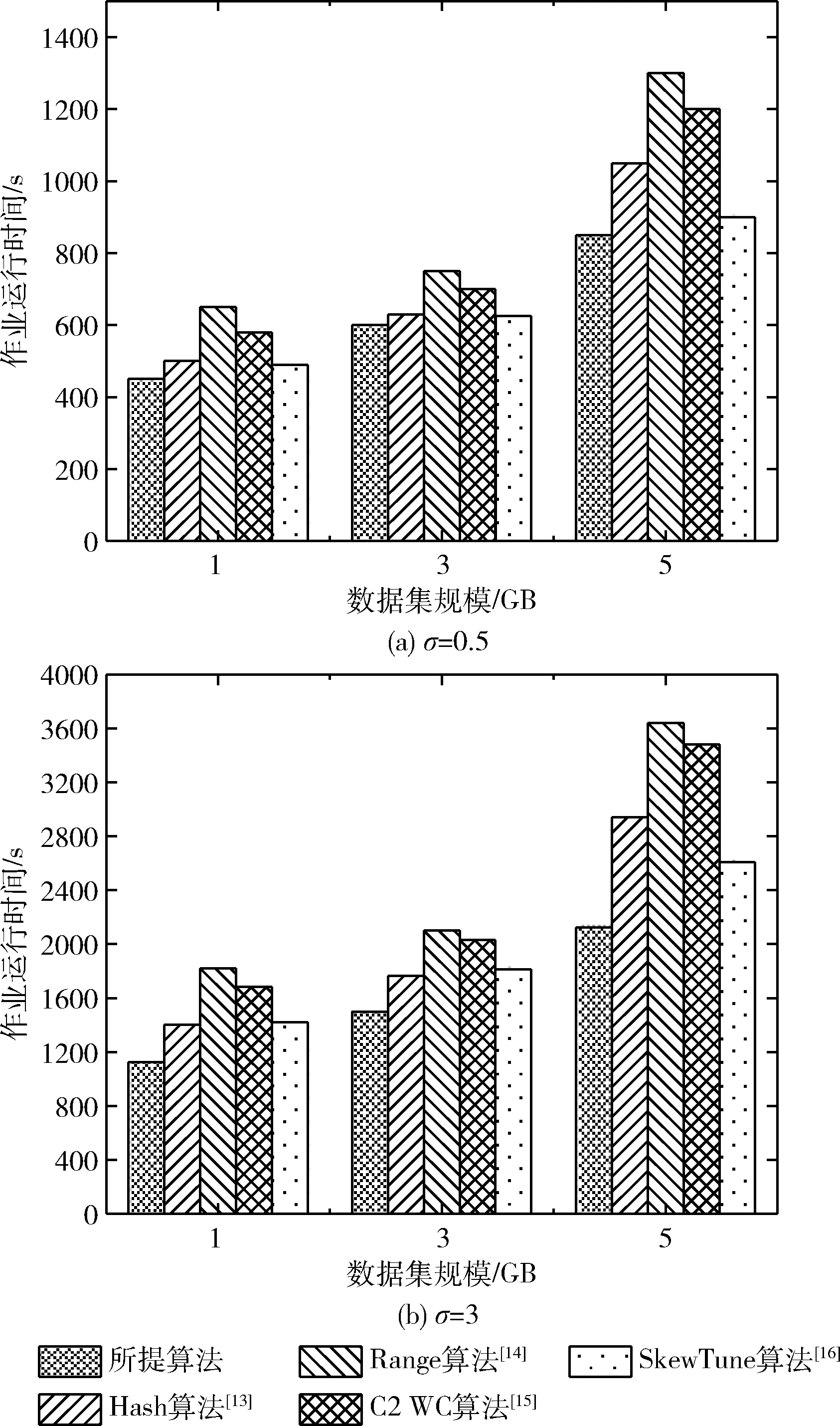
对于具有r个Mapper和s个Reducer的MapReduce框架,其可能的映射关系为sr种,当r和s数量较大时,搜索并建立Mapper与Reducer最佳映射关系可视为NP难问题。本文选择可变动作学习自动机进行最优映射关系构建。基本原理为:设B={b1,b2,…,bn}为一个有限动作集,且这组动作可以随时间的变化而变化。自动机可以从中选择动作,若在时间t暂时禁用某些动作,从而得到B′={b′1,b′2,…,b′n′}, 且n′ 学习自动机中规定,所有动作被激活的概率之和始终等于1[12],即 (5) 学习自动机算法中,活动动作总是基于其概率向量随机选择,并且基于环境响应,更新活动动作的概率。在更新活动动作的概率之后,自动机必须再次激活已被禁用的所有动作并更新概率向量,使所有行动的总概率等于1,更新公式如下 (6) 由于第1节中已然对Mapper的数据量进行了平衡处理,而Reducer的工作能力未知,显然若Reducer为同构的,则最佳的映射关系下所有的Reducer工作负载应相等;反之,若Reducer为异构的,则每个Reducer上的工作负载应与其所提供的处理能力成正比。 所提学习自动机的输入包含3个内容:①Reducer的数量;②每个Mapper的平均数据量,即Saverage;③Reducer可提供的计算资源。相应的,其输出则为Mapper到Reducer间的映射列表。不妨令学习自动机的集合定义为{LA1,LA2,…,LAr},每个学习自动机的动作集合为A={A1,A2,…,As},表示所选择的Reducer集合。每个自动机中,选择每个Reducer的概率记为p={p1,p2,…,ps}。所有自动机过程开始时,选择每个Reducer的概率是相同的且等于1/s。进一步地,令CS={CS1,CS2,…,CSr}表示Mapper上处理的数据集,RC={RC1,RC2,…,RCs}表示每个Reducer可提供的处理性能。因此,基于学习自动机的映射构建机制如下所示。 不失一般性,设Reducer数量为3,Reducer1、Redu-cer2、Reducer3上的期望负载比例为1∶1∶3,则RC可设为{RC1=1,RC2=1,RC3=3}。此种情形下,若要在3个Reducer上分配1200个Mapper的输出数据量,则可根据下式进行分配,即 (7) 式中:Porj为放置在第j个Reducer上的数量,WL={WL1,WL2,…,WLs}为Mapper的数据量大小。从而Reducer1、Reducer2、Reducer3的数据量为 (8) (9) (10) 如前所述,学习自动机的输出为一个具有s个成员的列表集合,不妨记为List={List1,List2,…,Lists},Listj表示发送到第j个Reducer。学习自动机算法在Map操作结束后迭代进行直至找到近似最优映射方案或达到迭代终止的阈值。 考虑到Reducer的计算能力差异性,定义如下的负荷变异系数对Reducer整体的工作负载进行度量,即 (11) 式中:STD(·)、AVG(·)分别为标准差和均值操作,workload为Reducer的负载集合。在同构Reducer环境下,最优映射建立时每个Reducer的工作负载相同,从而工作负荷变异系数为0;而异构Reducer环境下,最优映射关系下的COV应接近于0。 因此,所提迭代学习自动机流程如下: (1)学习自动机激活:CS集合中的每个成员进行迭代次数为r的循环迭代,学习自动机执行如下操作:当负载大于其未动作的部分时,激活对应的自动机动作并按式(6)进行概率更新。而每个Reducer分配的任务量则根据式(7)进行分配。 (2)Reducer映射确立:学习自动机根据其概率相量随机选择Reducer,例如Ae,即Reducere与CSi建立映射关系。从而将CSi的数据规模添加到workload集合中,并更新Reducer整体的数据规模。对每个CS重复上述过程。运行循环r次后,每个群集将被放置在Reducer上。 (3)映射方案评估,将新发现的解决方案的COV与最佳解决方案的COVbest进行比较。如果新解决方案的COV小于最佳解决方案的COV,则自动机的所有选定动作都会受到奖励,否则将受到处罚。每次迭代完成后具有最小的COV的映射方案保存为新的最优解决方案,并在下一次迭代过程中重新激活每个自动机的所有禁用动作,并根据等式(6)更新其概率向量。此过程继续,直到达到接近最优的解决方案或预定义的阈值。 算法最终返回的为有限迭代步骤下的最优解决方案。其中,时间复杂度为O(itrmax×r×s),其中itrmax为最大迭代次数。所提算法的步骤如下所示。 算法1:基于学习自动机的分区算法 输入:CS={CS1,CS2, …,CSr},RC={RC1,RC2, …,RCs},r 输出:List={List1,List2, …,Lists}为s列集合,初始值为∅。 假设: (1){LA1,LA2, …,LAr}为r个自动学习机,其中r是Mapper节点数量,每个自动学习机具有s个动作,s是Reducer数量; (2)令s个动作的概率矢量在所有的自动机中都初始化为同样的值1/s; (3)令Itrmax为最大迭代次数,ε为接近于0的值。 算法流程: 步骤1 初始化:itr=0;COV=∞;Sizeworkload=0//当前Reducer节点总负载大小。根据式(11)计算当前初始最优COVbest 步骤2 while(itr Begin Forj=1 tordo Begin Else 随机选择一个LAj的活动动作,如Ae,并根据式(5)更新LAj的概率矢量 workloade+=CSe×Sizee; Sizeworkload+=CSe×Sizee; Liste=Liste∪CSe。 End 根据式(11)计算COV If (COV 保存List集合作为新的可行解,COVbest=COV, flag=0; Else flag=1 End if Forj= 1 tordo Begin If flag==0,奖励选定动作LAj Else 惩罚选定动作LAj End if 启用所有禁用的动作并根据式(11)重构概率矢量 End itr++; END While 输出List={List1,List2, …,Lists} 为验证所提方案的可行性与优异性,本文在Hadoop 2.7.1环境下进行实验验证。其中,5台虚拟机配置与惠普 HPE ProLiant DL20Gen10服务器上,并采用KVM作为虚拟机管理程序,表1示出了虚拟机的配置参数。 表1 虚拟机参数配置 本节中,除特殊说明外所有实验均采用Hadoop中默认配置参数。此外,在所有实验中使用参数α=0.02的线性学习方案,并使用针对标准数据集的常用操作——文本数据集字数统计来分析所提数据倾斜处理算法的性能。其中,文本中的单词出现频率符合如式(12)所示的zeta分布,σ的变化范围为[0.5,3]。所有算法均运行20次并计算其平均值进行对比分析 (12) 本文选择如下算法作为对照实验: (1)传统Hash算法[13]:在Hadoop和Spark中用于数据分区的默认算法; (2)Range算法[14]:该算法分区结果为可变范围,并保留了Reducer分区顺序; (3)C2 WC算法[15]:该算法通过对MapReduce任务量进行采样并使用启发式方法进行Mapper任务量聚类组合; (4)SkewTune算法[16]:该算法在Mapper执行期间在检测落后计算节点的基础上在其它节点间分配剩余工作负载。 为了比较各算法的优劣性,采用如下指标: (1)作业运行时间。此参数等于作业完成时间减去作业开始时间; (2)负载变化系数。衡量Reducer节点间负载均衡度,根据式(11)计算; (3)负载极值比率。通过将Reducer节点上的最小工作负载除以最大工作负载得到。 首先按照式(12)生成大小为分别为1 GB,3 GB和5 GB的3组数据集,数据集的倾斜程度与σ成正相关关系。图3示出了σ=0.5和σ=3,数据量从1 GB到5 GB的作业运行时间。可以看出,在σ取值较小和σ取值较大两种场景下,5种算法随数据量变化的趋势相接近。在数据量较低时,5种算法的运行时长较为接近,随着数据量的增加,算法的运行时间均出现了明显的上升,而所提算法的运行时间比其它算法的上升幅度缓慢2.4%和15.8%以上。此外,显然在任何数据量规模下作业运行时间都小于其它算法的作业运行时间。这是由于本文所提算法采用提前传输机制与二次拆分方法,使已完成任务的Mapper节点在不等待其余节点完全工作结束后提前传输,并将规模较大的计算负载分摊至其它节点,从而节省了Mapper与Reducer间的传输时间以及Mapper的计算时间。因此,所提出的算法在处理数据倾斜问题中能具有更快的处理速度。 图3 不同算法下作业运行时间 进一步地,采用负载变化系数以及负载极值比率来分析不同算法下Reducer上工作负载的分布均衡度。如果COV的值接近于零,则意味着存在更平等的分布。而负载极值比率则反映了Reducer上的最小工作负载大小相对于分布在它们上的最大工作负载大小。该值越接近1,则最小工作负载与最大工作负载之间的距离越短,因此意味着发生更公平的分配。 图4(a)和图4(b)分别示出了不同数据集规模与不同zeta分布参数下Reducer节点的负载变化系数与负载极值比率,从上至下所用算法分别为:所提算法、传统Hash算法[13]、Range算法[14]、C2 WC算法[15]和SkewTune算法[16]。由图可知,所有算法中的负载变化系数与zeta分布参数σ和数据集规模大小成正相关性,而负载极值比例则与上述两个参数成负相关性。然而,当zeta分布参数固定,即数据倾斜程度相同时,所提算法相较于Hash算法、Range算法、C2 WC算法和SkewTune算法的负荷变化系数平均小31.96%、35.88%、44.36%、54.12%、62.01%;当数据集规模固定,即MapReduce所需处理的任务量固定时,所提算法相较于Hash算法、Range算法C2 WC算法、SkewTune算法的负荷变化系数平均小28%、33.3%、40%、48.57%和55%。类似的,zeta分布参数固定时,所提算法相较于Hash算法、Range算法C2 WC算法、SkewTune算法的负载极值比率大8.07%、9.72%、14.4%、22.91%和34.74%,而数据集规模固定时,所提算法相较于Hash算法[13]、Range算法[14]、C2 WC算法[15]和SkewTune算法[16]的负载极值比率大7.317%、8.974%、7.5%和8.07%。结合作业运行时间实验结果,表明所提算法在更短的运行时间内能够获取比其它传统算更优的执行性能。 图4 不同数据集规模与不同zeta参数下负载变化系数与负载极值比率 针对MapReduce平台下数据倾斜特性带来的Reduce阶段执行效率下降的问题,提出了基于布隆滤波二次拆分与学习自动机最优映射构建的数据倾斜处理算法。由于算法中采取已完成子任务提前传输机制、过载Reducer节点任务分摊机制与自动学习机迭代寻优机制,与传统数据倾斜处理算法相比,所提算法使Reducer节点能够在更短的工作运行时间里获得更小的负荷变化系数与更大的负荷机制比率,从而有效均衡了Reducer节点间的处理负荷。 由于本文假设数据集是真实可信的,因此,未来工作将着眼于数据真实性存疑时所提算法运行性能的提升研究。
2.2 算法流程
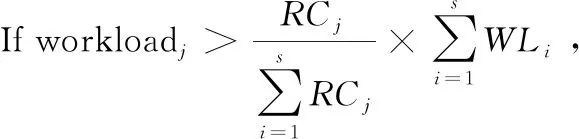
3 实验验证与结果分析
3.1 实验环境设置


3.2 评估指标
3.3 性能对比与分析

4 结束语

