基于波形净化技术的内陆湖泊波形重跟踪算法
黄征凯,汪海洪,温志强,陈志平
(1.华东交通大学 土木建筑学院,南昌 330013;2.东华理工大学 江西省数字国土重点实验室,南昌 330013;3.长江科学院 流域水资源与生态环境科学湖北重点实验室,武汉 430010;4.武汉大学 测绘学院,武汉 430079)
1 研究背景
卫星测高是成熟的水位观测技术,广泛用于全球海平面观测和冰盖监测[1]等领域。随着测高数据精度的提高以及数据处理方法的优化,测高技术也逐渐运用于监测内陆水体的水位变化[2-3]。然而,卫星测高技术研制最初针对于海洋环境,而在地形复杂或面积较小的湖泊的精度仍然有所局限[4]。
提高卫星测高数据精度的方法主要包括优化各种改正参数,如电离层延迟改正、对流层干湿分量改正以及其他地球物理改正项[5]等。波形重跟踪算法是另一种提高卫星测高数据精度的有效途径,国内外学者对此进行了大量的研究。传统的波形重跟踪算法主要针对于开阔水域和冰面条件[6]等,测高技术在近海区域的数据精度也较低,为此有学者针对近海区域提出了改进的波形重跟踪算法。鲍李峰等[7]采用函数逼近算法确定波形重跟踪改正参数,进而改善了测高卫星近海岸海面高精度;汪海洪等[8]提出了以聚类分析为基础的近海测高波形重跟踪的自适应方法。国外研究机构也发布优化后的近海和内陆水体测高产品,如PISTACH和ALES[9]等。近海区域精度较低的主要原因是受到陆地污染的影响[10],Tseng等[11]针对近海区域提出了一种波形修正技术,并通过试验验证了该技术能大幅提高测高数据精度。
内陆湖泊水域的测高精度限制与近海区域类似,即陆地反射效应引起的波形污染影响了卫星测高的观测精度,并且内陆湖泊的面积更小、地形较近海区域更为复杂。因此,本文针对内陆水域提出了改进的波形净化技术,并利用湖泊中水文站的实测水位数据进行精度检验。
2 近海区域的波形修正技术
当卫星地面轨迹接近陆地时,雷达回波受陆地反射信号的影响,在波形后缘中出现异常波峰。图1是轨迹编号为228的Jason-2测高卫星在近海区域的回波信号,图1(a)为11.55°N—11.95°N区域的波形采样数据集,平面坐标轴分别是纬度和波形采样点号,纵轴是回波功率;图1(b)和图1(c)分别为距岸0.5~2 km和2~8 km范围的波形,可看出在波形后缘中出现明显的异常峰值;图1(d)为距岸20~30 km的回波波形,形状近似于规则的布朗模型。
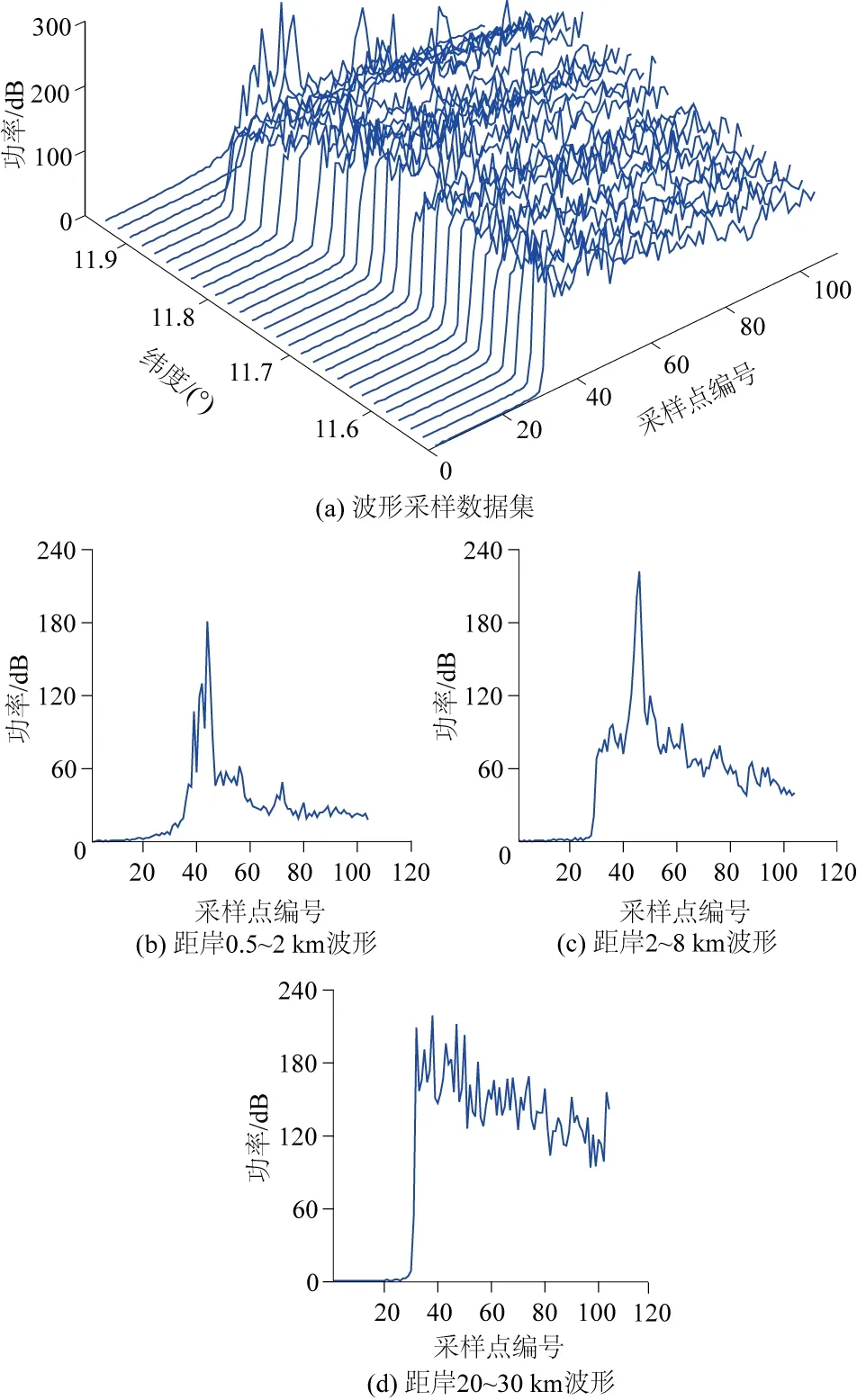
图1 近海区域的测高卫星返回波形Fig.1 Return waveforms of satellite altimeter in offshore area
汪海洪等[12]研究表明该异常信号将影响传统波形重跟踪算法对前缘中点的判断,并为此提出一种波形校正技术,用于剔除回波中的异常波峰。该技术主要原理是利用未受陆地污染的波形(距岸20~30 km)的平均波形作为参考波形(图2(a)),将近海波形依次与之比较,当差异大于一定阈值时,判定为异常点予以剔除(图2(b)),利用周围点内插值修复异常点的数据。实验结果显示,这种波形修正技术可有效提高近海区域重跟踪算法的精度。波形修正技术本质上不是直接改进重跟踪算法,而是修正回波中部分子波形。然而,该算法在内陆水域的波形重跟踪改正中仍有一定的局限性[13]。首先,波形修正技术的关键在于选取参考波形,利用距岸20~30 km的波形计算参考波形,与近岸波形差异较大,可能导致波形过度修正[12]。其次,回波中异常峰值周边的点很可能也受陆地污染的影响,利用这些点内插修复的结果可靠性也随之降低。
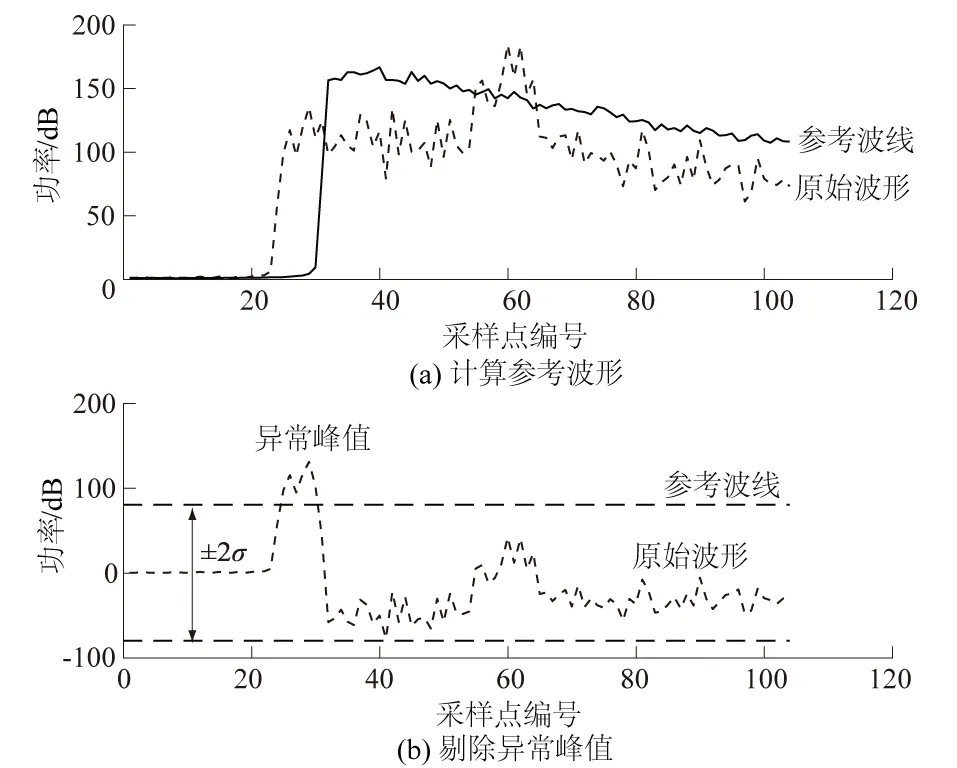
图2 利用波形修正技术探测异常波峰Fig.2 Detection of abnormal peaks by waveform adjustment technique
3 改进的波形净化技术
目前,卫星测高技术广泛应用于海洋学研究。由于受到内陆水域的面积所限,测高技术在内陆湖泊的观测精度远落后于传统水文观测手段。湖泊与近岸海域均为水陆交界区域,测高回波中受陆地污染的影响,可在上述波形修正技术基础上进行算法优化,并用于内陆湖泊的测高数据重跟踪改正。然而,波形修正技术主要针对近岸区域进行算法设计,多数内陆湖泊面积较小且地形更复杂,无法利用该算法计算参考波形。
上述波形修正技术中水陆交界区域波形修正的前提是利用开阔水域(20~30 km)计算参考波形,多数内陆水体并不满足该条件,因此该技术仅适用于近海或面积较大的湖泊。为此,本研究提出一种波形净化的技术,可用于消除内陆水域中的陆地污染引起的异常峰值。首先,本文改进了参考波形计算方法,即利用均值滤波消除异常波峰后的波形作为参考波形,用于净化测高波形。其次,对探测出的异常波峰不再用内插算法修复,而是直接赋予空值,避免波形的过度修正问题,利用优化算法对净化波形后的波形进行重跟踪改正。该方法的优点在于:①不需要利用开阔水域的波形数据提取参考波形,可用于净化多数小面积内陆水域的雷达回波;②每个波形的参考波形并不完全相同,实现了参考波形的动态选取;③利用滤波算法计算的参考波形与实际回波信号更为接近,既能修正雷达回波中的异常波峰,同时避免了由于波形过度修正导致的波形前缘偏移的问题。
图3为青藏高原扎日南木错中某周期的Envisat测高卫星的回波信号,图3(a)、图3(b)分别为利用波形净化技术处理前后的波形;横轴为波形的采样点,纵轴为沿轨迹方向排序的回波序号。从图3(a)可看出,在湖泊中间位置(波形序号30—60区域),波形中无明显的陆地污染效应,总体上接近布朗模型的波形特征。当测高轨迹靠近湖泊的边缘,波形后缘中逐渐出现异常波峰。图3(b)为净化后的波形。比较图3(a)、3(b)的色彩条可发现净化后波形功率值大幅降低。从图3(b)可明显看出靠近湖泊边缘的异常波峰被准确的探测并剔除。值得注意的是,湖泊中间位置的部分波形也出现了波形剔除现象。
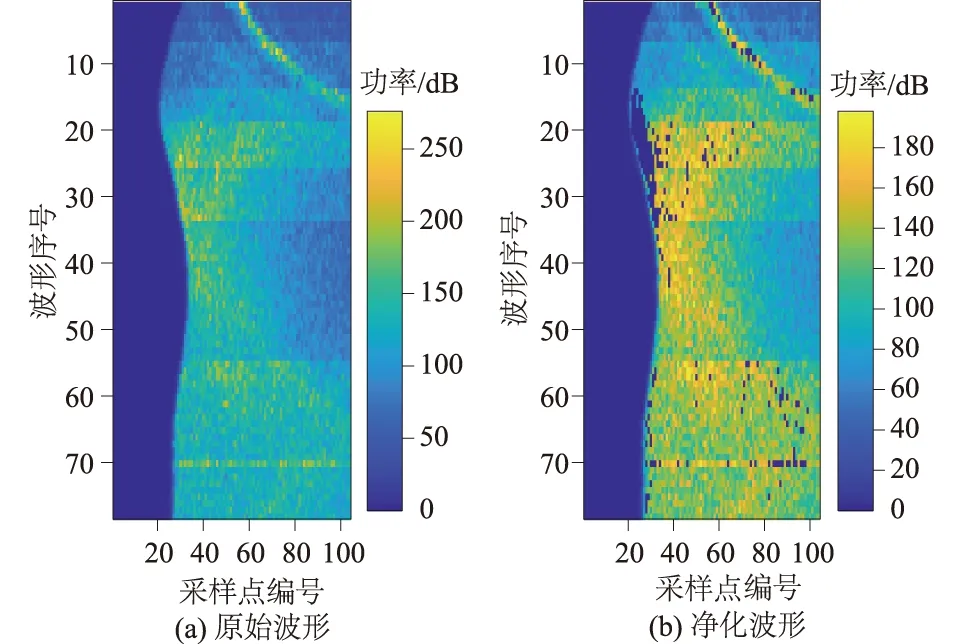
图3 Jason-2测高卫星途径扎日南木错的回波波形Fig.3 Return waveform while Jason-2 satellite approaching Zhari Namco
图4为从上述波形数据中选取的2个湖泊边缘的回波波形;其中图4(a)是距离陆地0~1 km的波形,波形呈“尖锥波形”(虚线),绿色线表示滤波算法计算的参考波形,红色线表示净化后得到的波形,净化波形只修剪了异常波峰部分;由于距离陆地的距离较远(1~7 km),图4(b)中异常波峰出现在波形后缘,利用参考波形消去了部分异常波形,而波形整体形状没有大幅调整。从图4中可发现2个不同位置计算的参考波形并不完全一致,由此说明本文提出的波形净化技术初步实现了参考波形的动态选取,这种方法能很好地探测出异常波峰,同时保证其余信号不被修正。
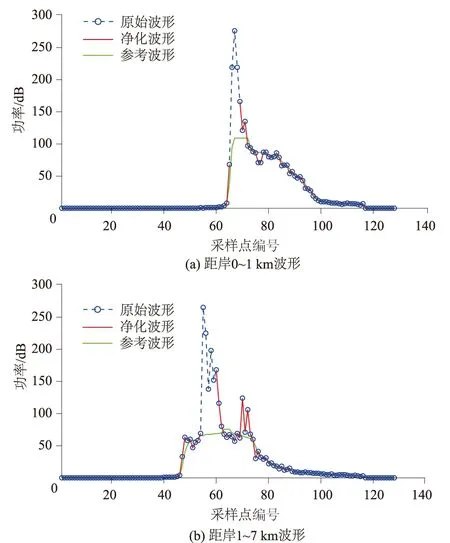
图4 探测回波波形中的异常波峰Fig.4 Detection of abnormal peaks in altimeter waveform
4 波形重跟踪算法实验
青藏高原地区分布着我国面积最大的湖泊群,由于自然环境和经济条件的制约,绝大多数湖泊中没有实测水文资料。本研究选取青藏高原少数布设水文站的湖泊作为研究区域,利用Jason-2和Enivsat测高卫星数据计算湖泊水位变化,并以实测水位数据分析波形净化技术在湖泊水位观测中的精度。图5为研究区域分布,分别介绍了途径青海湖、纳木错、扎日南木错和羊卓雍错等湖泊的测高卫星地面轨迹以及水文站的分布情况。在青藏高原地区(27°N—39°N),Jason-2测高卫星的轨迹间距较大(215~253 km),其地面轨迹仅通过其中的扎日南木错。因此,Jason-2测高数据仅用于计算扎日南木错的水位,其余3个湖泊均采用Envisat数据。由于青藏高原中多数湖泊无法获取长时间的水位观测数据,因此仅以上述4个青藏高原湖泊水文站数据作为外部检核资料,分析本文提出的波形净化方法的精度。表1列举了研究区域中测高轨迹编号、起止周期和水位数据起止时间。
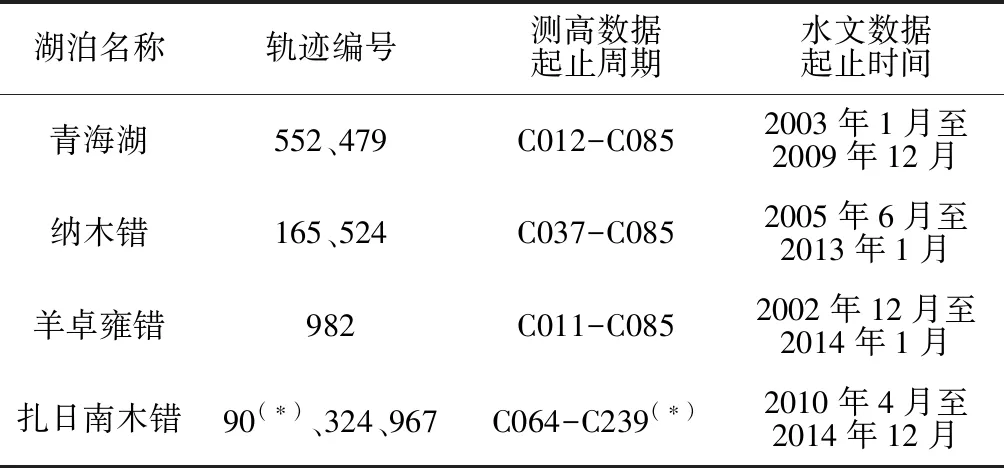
表1 改进波形净化算例中测高和水文数据Table 1 Altimetry and hydrological data in the improved waveform decontamination example
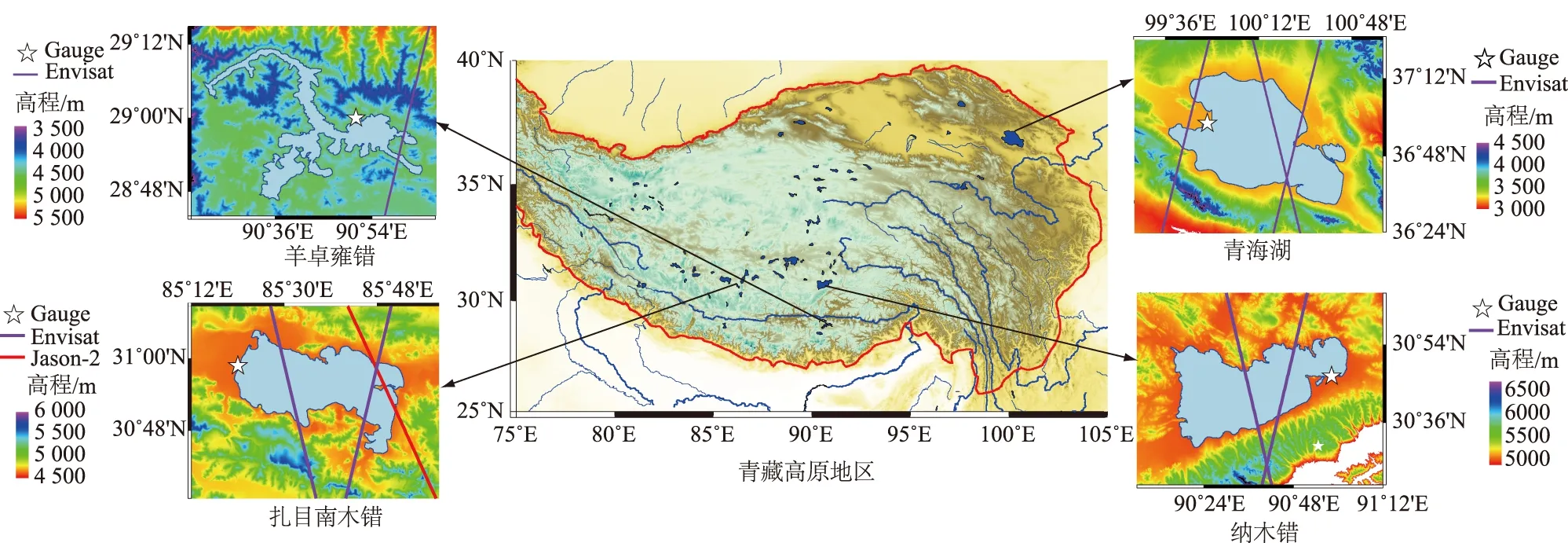
图5 研究区域分布Fig.5 Distribution of study area
图6为上述湖泊利用卫星测高技术获取的水位时间序列,图例中从左至右依次为实测水位数据、未改正的测高观测水位及用3种重跟踪算法(ICE-1、阈值法、波形净化和阈值法的组合方法)恢复的水位。从图6可看到,经过重跟踪改正后的测高数据均能取得和水文站观测较为一致的水位数据,其中青海湖和羊卓雍错中恢复的水位变化更加贴合。
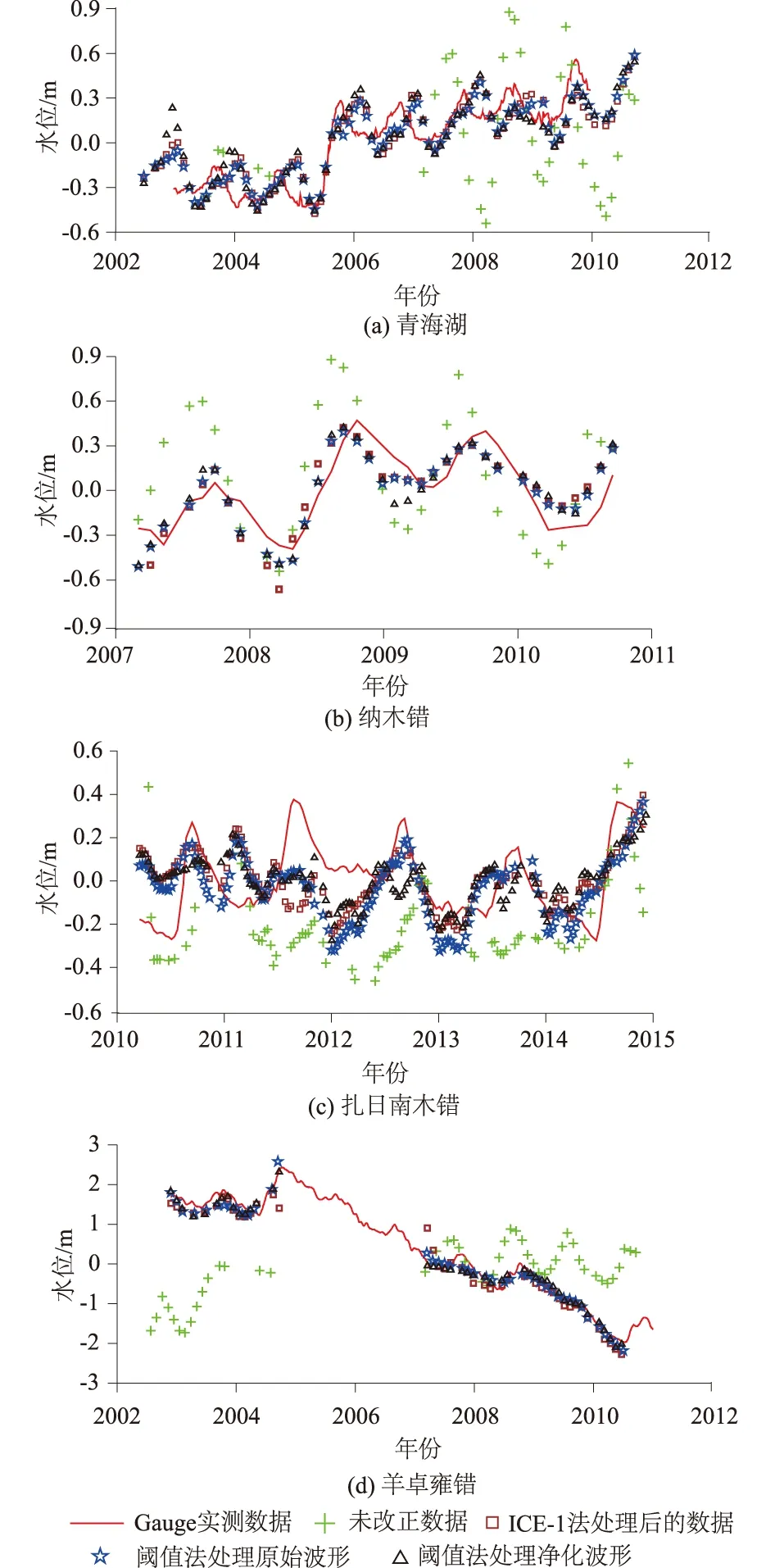
图6 利用各种重跟踪算法恢复湖泊水位时间序列Fig.6 Time series of lake water level retrieval by various retracking algorithms
表2统计了各种重跟踪改正的结果与实测水位数据的对比。从表2可看出,4个湖泊的测高观测数据精度均达到分米级。利用水文站和测高观测数据计算出湖泊水位变化速率,其中位于青海湖和纳木错为稳定上涨,速率分别为(11.7±0.45)cm/a 和(5.5±8.2)cm/a;扎日南木错表现为略微上涨,速率为(0.6±1.4)cm/a;羊卓雍错则为快速下降,速率为(-46.5±4.0)cm/a。
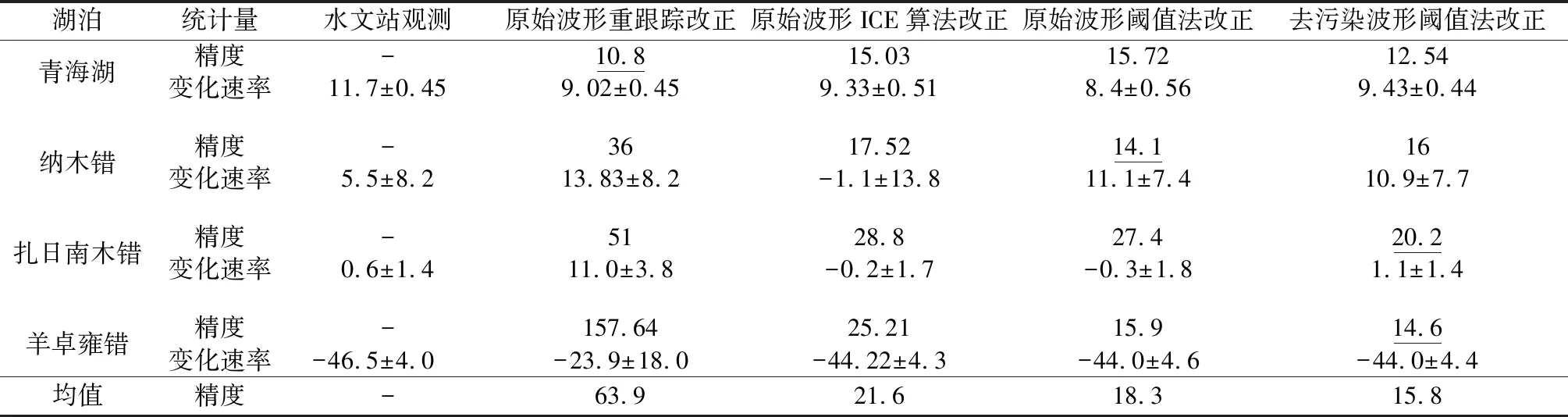
表2 利用测高技术获取部分青藏高原湖泊水位精度统计Table 2 Statistics of water level accuracy of some lakes in the Qinghai-Tibet Plateau using the altimetry technology
综合研究区域的实际情况和实验结果可知,由于青海湖和纳木错的水域较为开阔,用于计算水位变化的轨迹较长(约为60 km和25 km),仅通过简单的剔除湖泊边缘的观测数据,即可获得较为精准的水位变化信息。在青海湖和纳木错中,分别是未重跟踪改正和对波形进行阈值法改正计算湖水位与实测水位数据最接近(精度分别为10.4 cm和14.1 cm)。上述2个湖泊的波形净化过程中,由于部分湖泊中间区域的波形被过度净化,从而影响重跟踪算法对波形前缘的判定,因而这2个湖泊中波形净化方法的精度较低。相反,在扎日南木错和羊卓雍错的测高轨迹长度较短,“陆地污染”效应对测高回波信号有明显的影响,未经重跟踪改正的测高数据精度极差,在羊卓雍错的精度甚至只有157.64 cm。在这2个湖泊中,对净化后的波形进行阈值法改正获取的水位数据精度表现最好,分别为20.2 cm和14.6 cm。实验结果表明,利用本文提出的波形净化技术消除回波中“陆地污染”产生的异常波峰后,利用阈值法进行重跟踪改正,可大幅提高测高数据精度。
本实验利用Jason-2和Envisat测高卫星计算4个青藏高原湖泊水位变化,并与水文站数据进行比较,以分析内陆水域改进波形净化技术的可行性。从实验结果中看到,结合波形净化技术和阈值法处理测高数据获得的水位与水文站的观测结果更加一致,研究区域的平均精度达到15.8 cm,较ICE-1算法和阈值法分别提高了14%和27%。
5 结 论
我国仍然有大量湖泊缺少水文观测资料,尤其是在经济不发达的偏远山区,卫星测高技术作为成熟的水位观测技术可用于补充地面水文站的数据空白。由于测高卫星经过水陆交界处时,受到“陆地污染”的影响,雷达回波中出现的异常峰值,会影响传统波形重跟踪算法对波形前缘的判断,制约了测高技术在内陆湖泊的水位观测精度。本文在近海水域波形修正技术的基础上,针对内陆水域面积有限的特点,提出改进的波形净化技术,有效地消除了测高回波信号中的异常峰值,实验表明该方法可有效提高内陆湖泊的测高数据精度。
在本文中,部分面积较大的湖泊中出现波形被过度净化的现象,在后续的研究中可尝试利用自适应算法进行波形分类,并确定是否需要进行波形净化处理,或者通过测试不同的滤波方法或者组合多种波形重跟踪算法来解决这一问题。此外,单一测高卫星的重复周期为10 d甚至更长,无法获取更高时间分辨率的湖泊水位变化信息,融合多源测高数据是解决该问题的有效方法,目前大量运行的测高卫星计划为这一研究提供了重要的数据基础。

