考虑损伤缺陷的颚式破碎机齿轮传动寿命预测方法

刘永平

(宁夏东方钽业股份有限公司，宁夏 石嘴山 753000)

破碎作业是将大块物料加工成小块物料的过程，完成该作业的设备为破碎机械[1]。破碎作业广泛存在于矿山、冶金等行业中，在经济发展中具有重要作用。根据设备架构与工作机制的不同，破碎机械分为颚式破碎机、圆锥破碎机、冲击式破碎机等，其中颚式破碎机是最为常用的作业机械之一，具有噪声低、粉尘少、运行费用低等优势。磨损是影响颚式破碎机寿命的关键因素之一，在破碎机齿轮传动过程中，轮齿过度磨损不但会影响齿轮传动精度及速率，还会造成机械振动，产生噪声，甚至会导致齿轮断裂，造成重大事故[2]。为了最大限度地改善颚式破碎机的整体性能，预测其齿轮传动寿命是十分必要的。

针对颚式破碎机齿轮传动寿命的预测问题，文献[3]提出了一种基于非线性数据融合和多阶段退化的设备寿命预测模型，利用神经网络理论中的自编码器对表征设备退化的多维参数进行融合，构建设备退化指示量，采用CUSUM算法提取出设备退化过程中的分段点，建立多阶段维纳退化模型实现设备寿命预测，但该方法计算过程繁琐，且误差较大，时效性不高；文献[4]运用粒子滤波算法设计了一种寿命预测方法，采用多模型方法对机械设备运行过程进行建模，克服传统单一模型难以描述其生命变化周期的缺陷，借助粒子滤波算法和系统模型切换矩阵，预测系统运行状态，最后为提高预测精度，使用预测偏差补偿算法，达到无偏预测的目的，但该方法在预测过程中没有考虑机械设备整体状态，计算结果可靠性较差。

针对以上方法的不足，本文提出了一种基于损伤缺陷的颚式破碎机齿轮传动寿命预测方法，探究颚式破碎机齿轮传动失效原因，建立损伤树模型，并引入关联度计算，明确设备失效的具体位置，为后续齿轮传动寿命预测奠定基础。在初始数据基础上构建无偏灰色模型，代入马尔可夫优化，有效提高了寿命预测精度。

1 基于损伤树的颚式破碎机齿轮损伤缺陷定位

基于损伤树进行分析时，影响顶事件发生的底事件包含不同的组合，将各组合称作一个割集。最小割集表示顶事件可能发生的最小限度集合，是描述引发损伤树顶事件损失的一种方式[5-6]。若最小割集内的基础事件都已发生，必然会发生顶事件。

假设具备K个典型损伤，各类典型损伤通过若干特征参变量组成一个特征矢量XRj(k)，其中Rj为第j个损伤特征集合，k为损伤时段，将K个特征矢量构成的典型损伤矩阵记作[XRj(k)]K。如果有P组待检测数据，它们组成的待检测数据特征矩阵为[XTi(k)]P，其中Ti为第i个待检测数据集合。

各特征矢量均表示一种损伤形式，其基础工作原理如图1所示。

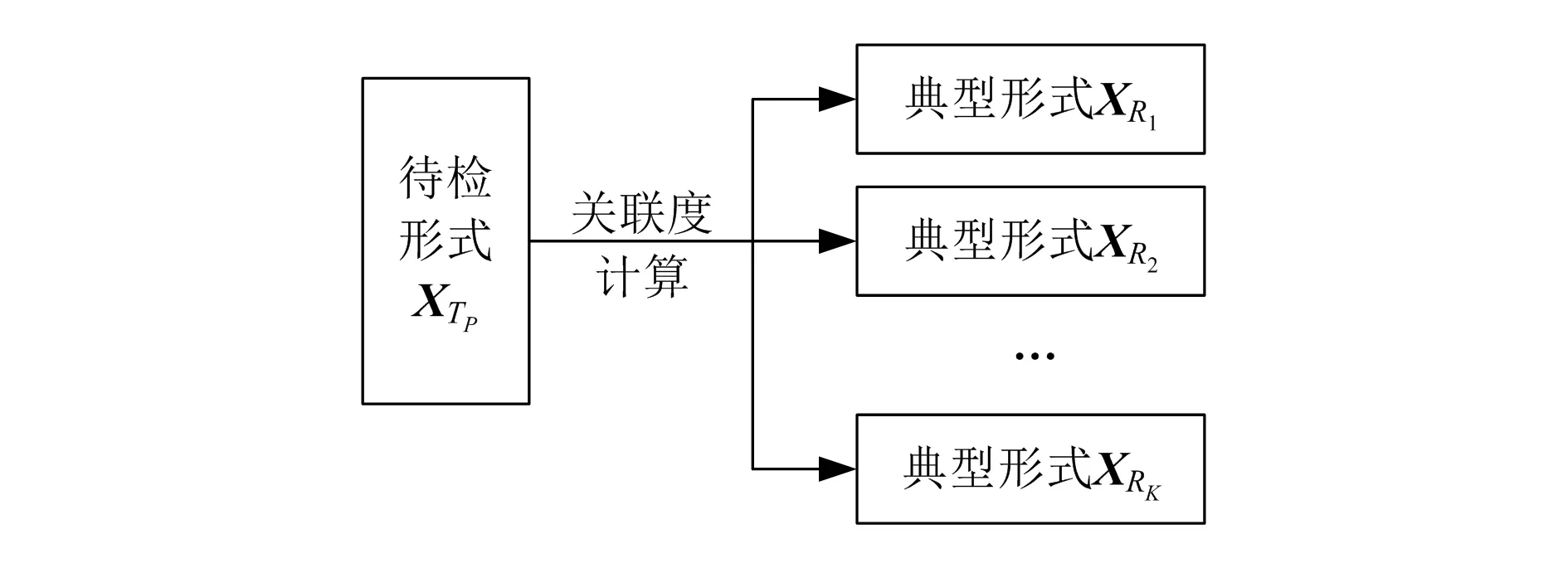
图1 工作原理示意图

设第i个待检测形式矢量是{XTi}，利用{XTi}和典型形式矢量{XRj}之间的关联度运算得到关联度序列{γTiR1,γTiR2,…，γTiRK}。关联度计算过程如下：

(1)

(2)

式中：εTiRj(k)为关联度系数；ΔTiRj为k时段两个数列的绝对差；ρ为分辨系数，其取值通常为[0,1]。

设T代表顶事件，即损伤现象，m表示损伤树最小割集数量，底事件是Xi。若发生顶事件，则把该事件结构函数记作：

φ(X)=φ(X1,X2,…，Xn)=

(3)

第i个最小割集Ti由ni个底事件构成，组成特征矢量[XTi(1),…,XTi(n)]。在最小割集Ri内，让ni个底事件全部是1，剩余的(n-ni)个底事件是0，由此m个最小割集就组成一个典型损伤特征矩阵[XTi(k)]m×n。

想要获得致使损伤树顶事件发生的各类损伤形式产生概率，可从底事件的关键性进行研究。结构关键性代表底事件在损伤树内重要地位对顶事件产生的影响[7]，具体描述为：

(4)

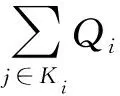
{Xz}={Xz(1),Xz(2),…，Xz(n)}=

{e1,e2,…,en}

(5)

利用{Xz}和典型模式矢量{XTi}间的关联度运算，即能获取关联度序列，由此完成齿轮损伤缺陷定位，有效获取齿轮的真实状态，为齿轮传动寿命预测奠定基础。

2 基于马尔可夫的齿轮传动寿命预测

根据最终残差值明确未来预测值区间。采用马尔可夫优化，通过最终残差值落入各状态的点算出下一步转移概率矩阵，来评估未来变化趋势，把初始数据模拟值与残差预测值相加就得到最终的模拟值[8]。无偏灰色GM(1,1)模型构建流程如下。

将非负初始数据序列X(0)从小到大排序：

X(0)={x(0)(t1),x(0)(t2),…，x(0)(tm)}

(6)

式中：x(0)(ti)为齿轮失效寿命。

为弱化初始数据随机性，利用累加可挖掘出数据的规律，对X(0)采取一次累加处理获得全新的数据序列X(1)：

X(1)={x(1)(t1),x(1)(t2),…，x(1)(tm)}

(7)

(8)

为了让新生成的序列具备平滑性[9]，对该序列进行紧邻生成操作：

Z(1)={z(1)(2),z(1)(3),…，z(1)(m)}

(9)

t=2,3,…，m

(10)

式中：Z(1)为紧邻系数；z(1)(t)为紧邻函数。

构建无偏灰色动态GM(1,1)模型，模型的微分方程为：

(11)

式中：x(1)为累加获得的全新齿轮数据；b，c分别为参变量和内部变量。采用最小二乘法能够求解出参变量b与内部变量c的值：

(12)

(13)

(14)

求解参变量a及A的值，把拥有指数转变趋向的初始数据x(0)(tk)进行一次累加，得：

(15)

(16)

通过传统灰色GM(1,1)模型构建能够得到式(16)，从而计算出a与A的值，分别为：

(17)

(18)

把无偏灰色GM(1,1)模型的竖直模拟值记作：

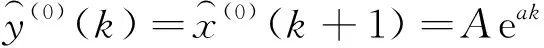
k=1,2,…,m-1

(19)

运用式(19)获取的模拟值偏差较多，可通过构建残差值绝对值的无偏GM(1,1)模型进行校正[10-11]。首先按照模拟值与真实模拟值推算残差值与相对偏差：

(20)

(21)

式中：ε(0)(k)为残差值；x(0)(k)为采用无偏灰色GM(1,1)模型获得的真实模拟值；η为相对偏差。

将残差值ε(0)(k)的绝对值进行一次累加处理，得到：

(22)

ε(1)(ti)={ε(1)(t1),ε(1)(t2),…,ε(1)(tm)}

(23)

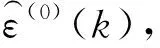
把最终残差值分割为多个子序列，然后按照最终残差值特征将其分成若干状态，依次记作⊗1，⊗2，…，⊗m，状态分割个数与样本个数相关。

利用式(24)计算状态转移概率：

(24)

式中：Mij(k)为通过状态⊗i使用k步转移至状态⊗j的齿轮疲劳寿命数据样本个数；Mi为状态⊗i内齿轮疲劳寿命数据样本个数；Pij(k)为状态⊗i通过k步转移至状态⊗j的概率。创建m步状态转移概率矩阵P(k)：

(25)

式中P(k)呈现出状态之间的转移规律，运用原始状态与P(k)能够明确未来齿轮传动发展方向。利用一步状态概率矩阵P(1)可了解被预测目标的下一步转移状态[12]，也就是将最高概率所在的状态当作未来齿轮传动的状态。

确立转移状态⊗i之后，得到预测值变动区间为：

(26)

最终得到齿轮传动寿命预测公式为：

(27)

由上述过程即能得到精准的齿轮传动寿命预测数值，为颚式破碎机稳定使用及故障维修提供坚实保障。

3 仿真实验

将颚式破碎机内的直齿圆柱齿轮当作实验对象，使用本文所提方法探究齿轮传动磨损寿命。

图2是齿轮传动轮齿间啮合点对应滑移速率伴随啮合压力角变化的曲线图。齿轮包括主动轮与从动轮，由于齿轮传动受真实啮合线限制，因此啮合压力角有固定的取值范围。由图2可知，齿轮间对应滑移速率在主动轮齿根和从动轮齿顶刚接触时最高，随着啮合点的转移，滑移速率逐渐下降，在节圆位置为零，这是因为在节圆位置轮齿间是纯滚动。超过节圆位置后，对应滑移速率逐步升高，但方向为负方向。

图2 啮合点的对应速率

图3所示为齿轮传动过程中齿间接触应力曲线，由图可知，伴随啮合压力角增加，主动轮啮合点从齿根向齿顶移动，齿间接触应力逐渐减少，但数值改变不多，证明齿轮传动平稳时，轮齿内每个点承受的接触应力差距较小。

图3 啮合点接触应力示意图

图4所示是齿轮内各点磨损后曲率半径变化的情况，图中实线是磨损前各点曲率半径，虚线是磨损后曲率半径。通过比较可以看出，由于磨损齿廓内每个接触点曲率半径都会变小，齿根和齿顶的变化较大，节圆位置变化较小，证明齿轮传动啮合时，齿根和齿顶周边磨损较为严重，这也是致使齿轮传动失效的重要部位。

图4 磨损后曲率半径变化状态示意图

根据上述颚式破碎机直齿圆柱齿轮的相关数据进行实验验证，以损伤缺陷位置的检测准确性与齿轮传动寿命的预测精度为实验对比指标。

3.1 损伤缺陷检测

损伤缺陷检测是准确预测寿命的重要前提，采用本文所提方法对齿轮损伤缺陷进行检测，结果如图5所示。

从图5可以看出，本文所提方法的损伤缺陷检测结果与实际情况基本一致，能够准确检测齿轮损伤缺陷，为预测齿轮传动寿命打下坚实基础。

3.2 齿轮传动寿命预测

图6为固定转速下齿轮传动寿命随转矩变化的曲线图，图中带*点线表示不同转矩工作状态下多次仿真获得的齿轮磨损寿命初始曲线，另一条曲线是对初始曲线进行拟合获取的预测拟合曲线。

图5 损伤缺陷检测

图6 本文方法下齿轮传动磨损寿命预测示意图

从图6可知，在固定转速下，齿轮磨损寿命随转矩的增大而减少，原始转矩从小变大过程中，齿轮磨损寿命变化较为明显，在转矩达到一定值时，齿轮传动磨损寿命变化才逐步稳定。由此说明本文方法可有效呈现齿轮磨损真实状态，预测结果较为精确。

4 结束语

针对颚式破碎机齿轮传动失效问题，本文提出了一种基于损伤缺陷的颚式破碎机齿轮传动寿命预测方法，所提方法可有效提升齿轮传动寿命预测准确性，为颚式破碎机合理运用奠定基础。但在计算设备损伤缺陷时，仅能依靠领域专家诊断经验进行损伤树构建，有较强的主观性，可能导致计算结果精确度不高，在接下来的研究中将对此问题进行改进。