粗糙度对高速电主轴温升的影响

雷春丽，赵明齐，贾希斌，巩宝儒

(兰州理工大学机电工程学院，甘肃 兰州 730050)

电主轴作为机床的关键部件，对机床的整体加工性能起着决定性作用。电主轴内置电机和轴承的发热不可避免，由此引起的热变形若得不到及时处理，会严重影响电主轴的加工精度。因此，对电主轴温升及热变形的研究是十分必要的。

国内外学者对电主轴热态特性进行了研究。Bossmanns等[1]建立了高速电主轴的有限差分热模型，并基于此模型对电主轴进行了稳态和瞬态温度场分析；Holkup 等[2]用有限元方法建立了电主轴的热-机耦合模型，经过实验验证的热-机耦合模型可以预示实际工作状态下主轴温度分布、热位移；陈小安等[3]建立了一种考虑系统热响应和预紧方式影响的角接触球轴承热-机耦合动力学模型，分析了运行状态下主轴轴承的摩擦损耗及动态支承刚度，理论计算和试验结果表明模型具有足够的精度；邢军强等[4]基于3D流场模型对转子空气摩擦损耗与电机转子转速、表面粗糙度等进行了分析，并通过实验验证了方法的有效性。另外，文献[5]～[8]利用有限元分析软件对电主轴进行热-结构分析，得到了电主轴温升和热变形的变化规律。综上所述，虽然对电主轴热态特性模型的研究取得了丰硕的成果，但具体分析定转子表面粗糙度因素对电主轴热态特性影响的文献较少。本文基于有限元方法，在考虑定、转子表面粗糙度对电主轴换热系数及空气摩擦损耗影响的基础上，建立了电主轴单元模型，详细研究了考虑定、转子表面粗糙度时电主轴系统温度场及热变形的分布规律。

1 电主轴生热模型的建立

电主轴系统中，内部热源主要有电机损耗发热和轴承摩擦生热。为了更贴合机床电主轴实际运转状况，热源计入空气摩擦损耗及附加损耗。

1.1 电机损耗发热

电机位于主轴单元体内，自然散热条件较差。电机在实现能量转换的过程中，其内部产生功率损耗，从而使电机发热。研究发现，在电主轴高速运转情况下，近2/3的热量由定子产生，1/3的热量由转子产生。

1.2 轴承摩擦发热

轴承的发热主要和摩擦力矩有关，力矩越大，生热越多。根据Palmgren摩擦力矩经验公式[9]，轴承的摩擦力矩由润滑剂黏性产生的摩擦力矩M0和与速度无关的载荷作用产生的摩擦力矩M1组成，轴承发热功率则是两类摩擦力矩之和与轴承角速度的乘积，公式为：

(1)

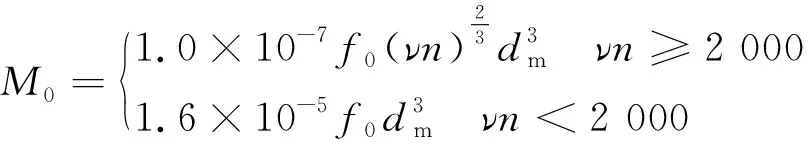
(2)

M1=f1P1dm

(3)

式中：Hf为轴承的发热功率；n为主轴转速；f0为与轴承设计和润滑有关的系数，对于角接触球轴承，采用油气润滑时，f0=1；ν为润滑油在运转温度下的运动黏度；dm为轴承节圆直径；f1为与轴承类型和所受负荷有关的系数；P1为确定轴承摩擦力矩的计算负荷。

f1=1.3×10-3(P0/C0)0.33

(4)

P1=Fa+0.1Fr

(5)

式中：P0为轴承当量静负荷，P0=0.5Fa+0.46Fr；Fa为轴承的轴向负荷；Fr为轴承的径向负荷；C0为轴承的额定静负荷。

由于润滑油黏温效应的存在，随着温度的升高，其运动黏度不断降低。轴承常用的机油型号为32#，其不同温度下的运动黏度可以表示为：

ν=32e-0.024 2(T-40)

(6)

式中：T为润滑油温度。

1.3 空气摩擦损耗及附加损耗

高速电主轴运转过程中，在定、转子间隙中存在着空气摩擦损耗。空气摩擦损耗Pwin与定子和转子的表面粗糙度、转子转速、空气流速、定子和转子的间隙等有关，其计算公式为[10]：

(7)

式中：Cf为空气摩擦阻力系数；ρ为空气密度；ω为转子的角速度；D为转子的直径；l为转子的长度。

高速电主轴转子表面的粗糙度一般为3 μm[11]。本文分别计算了定、转子表面粗糙度为3，4，5，6 μm时对空气摩擦损耗的影响。因它们变化趋势一致，故在此仅详细描述表面粗糙度为3 μm和6 μm时对空气摩擦损耗的影响，计算结果如图1所示。

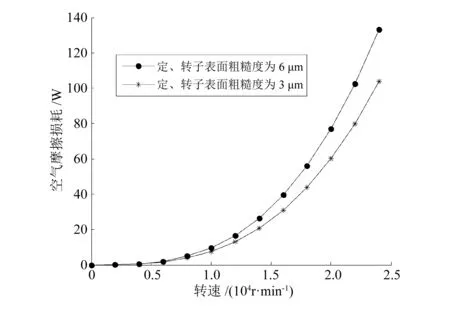
图1 不同粗糙度下空气摩擦损耗随转速的变化

由图1可知，随着主轴转速的增加，转子与周围空气的相对速度增大，空气摩擦损耗也逐渐变大。同时可看出，与定、转子表面粗糙度为3 μm时相比，粗糙度为6 μm时其空气摩擦损耗随转速增加变化较快。因此，在电主轴高速运转过程中，空气摩擦损耗不可忽略。

附加损耗通常是按生产时间中积累的经验数据选取。电主轴在空载运行时，取额定功率的1%～5%作为附加损耗。

2 边界条件

由热力学第一定律可知，电主轴热边界条件主要有热对流、热辐射和热传导3种，其中对流换热是其与周围环境热交换的主要方式。

2.1 定、转子之间气隙的对流换热系数

考虑到定、转子表面并不是绝对光滑的，在计算定、转子气隙内的换热系数时，不可忽略表面粗糙度对摩擦阻力和散热的影响。故努谢尔数Nu[10]可由式(8)求得：

(8)

(9)

式中：Cf2为转子空气摩擦阻力系数。当定、转子表面粗糙度相同时，可按下式计算摩擦阻力系数：

(10)

式中：δ为气隙长度；h为转子表面粗糙颗粒高度。进而可推导出换热系数hsr为：

(11)

式中：λ为空气的导热系数。

根据式(8)～式(11)，可得出定、转子表面粗糙度与换热系数的关系，如图2所示。

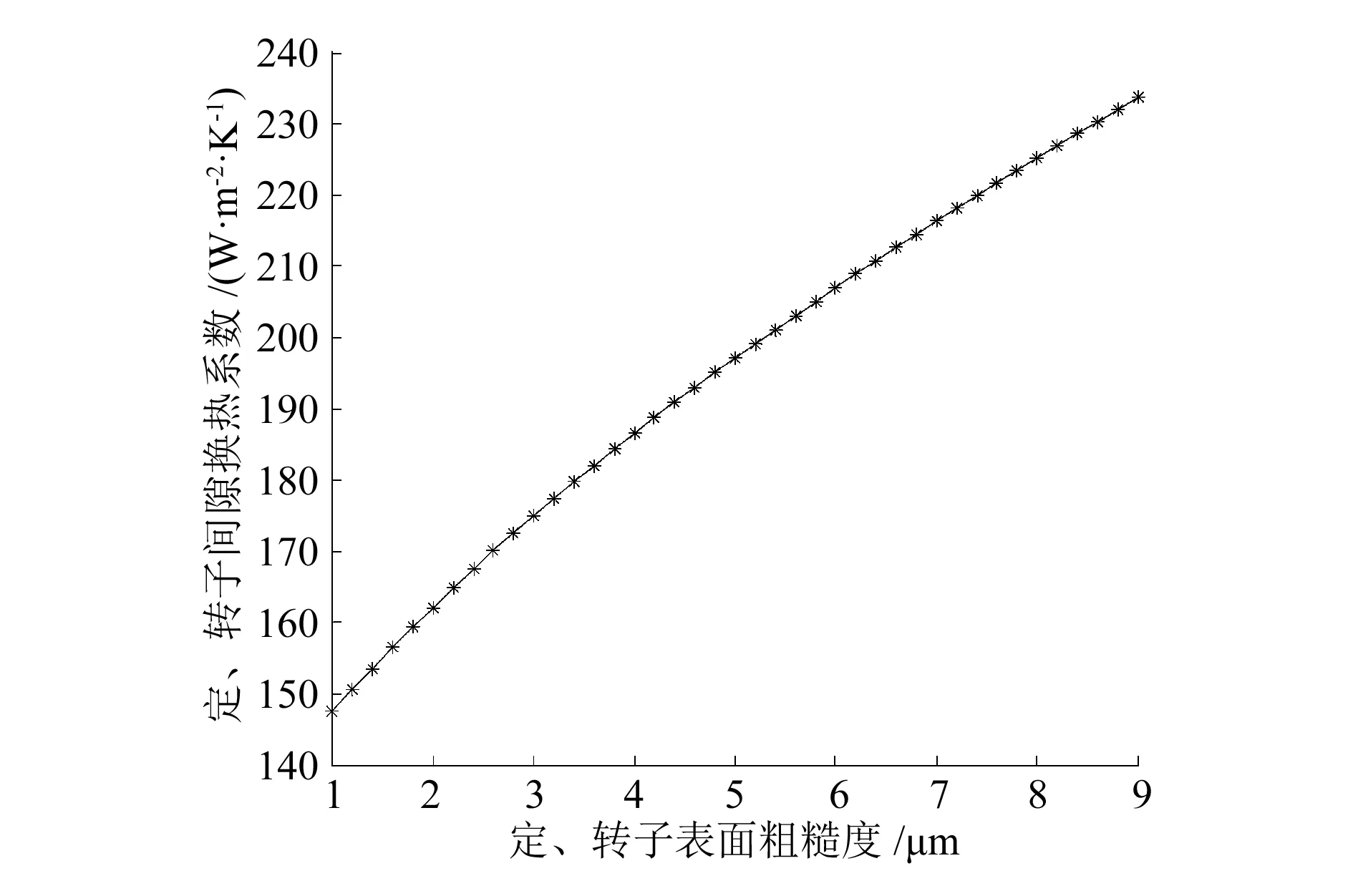
图2 定转子表面粗糙度对换热系数的影响

从图2可看出，随着定、转子表面粗糙度的增加，定、转子间气隙的换热系数不断增大。

2.2 转子端部与空气的对流换热系数

电主轴运转过程中，转子端部与周围的空气发生对流换热和辐射换热，其计算公式为：

(12)

式中：hz为转子端部与空气的对流换热系数；vz为转子端部的平均速度。

2.3 轴承与油气润滑气体之间的换热系数

轴承进行油气润滑时，所需要的油量很小，因此假定热交换只发生在轴承和压缩空气之间，忽略被润滑油吸收的热量。由于压缩空气为紊流射流，在向轴承喷射时，使得轴承受到附加的轴向气流，因此轴承与油气润滑对流换热系数是主轴转速和压缩空气流量的函数，可由多项式函数α拟合：

α=c0+c1uc2

(13)

式中：c0，c1，c2为实验测得的常数，分别取9.7，5.33，0.8；u为轴承中空气的平均流动速率。

(14)

式中：v1为通过轴承的轴向气体流量；Aax为气流流过气隙的面积；dn为轴承的平均直径。

2.4 冷却套与冷却水之间的对流换热系数

定子外分布有矩形螺旋冷却水套，对定子产生的热量进行吸收和冷却，其换热方式属于管内流体强迫对流换热。由于冷却水在管中的流态不同，其对流换热系数计算公式[12]也不同。

2.5 电主轴与外部空气之间的换热系数

电主轴外表面和周围环境的对流分为两部分：一是主轴外表面的非旋转部分与周围环境的对流换热；另一部分是主轴头部运动外表面与周围空气的对流换热。

电主轴与周围的空气同时进行着对流和辐射传热。电主轴外壳静止，表面与周围的空气之间的传热为自然对流换热，其传热系数也反映了辐射传热的影响，取复合传热系数hs=9.7 W/(m2·℃)。

主轴头部运动表面与空气的对流换热系数h可按下式计算：

h=c0+c1u1c2

(15)

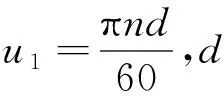
3 电主轴有限元仿真分析

3.1 高速电主轴有限元模型

仿真分析采用的电主轴型号为170SD24Q15，其最高转速为24 000 r/min。为了便于分析，对电主轴系统的结构进行一定的简化处理。电主轴是轴对称结构，为了更好地观察每个部分的仿真结果，进行整体建模。

基于ANSYS15.0设置材料密度、弹性模量、比热容等参数，并进行网格划分，得到1 368 569个节点和591 356个单元。电主轴网格模型如图3所示。

图3 电主轴网格模型

3.2 仿真分析条件

数值模拟时的条件如下：1)环境温度为20 ℃；2)水冷系统入水口温度为17 ℃，出水口温度为25 ℃，冷却水流量为8 L/min，主轴转速为20 000 r/min；3)润滑方式采用油气润滑，压缩空气压力为0.5 MPa。

根据生热率和传热公式可得相应的电主轴边界条件参数，具体数值见表1。

表1 电主轴边界条件

3.3 电主轴温度场分析

基于Workbench中Steay-State Thermal模块对电主轴有限元模型加载生热率及边界条件，其中生热率是通过体积载荷加载到前、后轴承及定、转子上，换热系数通过面载荷进行加载。然后对模型进行仿真，得到电主轴温度场分布图。

由于低转速时，定、转子表面粗糙度对空气摩擦损耗的影响可忽略，因此考虑主轴高转速，即转速为20 000 r/min时，分析定、转子表面粗糙度分别为3 μm、6 μm时的主轴温度场分布规律。图4为不同粗糙度下的电主轴温度场分布图。

图4 不同粗糙度下温度场分布图

从图4可知，定、转子表面粗糙度为3 μm时，其最高温升为56.654 ℃，高于6 μm时的最高温升55.103 ℃。这是因为随着定、转子表面粗糙度的增加，定、转子间隙换热系数和空气摩擦损耗均不断增加，但定、转子表面粗糙度为3 μm时，定、转子间隙换热系数小于6 μm时的换热系数。电主轴温度场最高温升随着粗糙度增加有下降趋势，这表明定、转子间隙换热系数对最高温升的影响比空气摩擦损耗对温升的影响更明显。

为了研究电主轴系统各个时刻各部分的温度变化情况，通过Transient Thermal模块实现瞬态热求解，其他参数和边界条件与稳态热分析保持一致。

设定求解时间为3 000 s,取电主轴定子上一个关键点,描绘出其温度随时间的变化曲线，如图5所示。

从图5可知，定子温度在1 000 s之前上升较快，大约在1 500 s时达到热平衡。定子最高温升的变化与温度场最高温升变化一致，即定、转子表面粗糙度小的温度比粗糙度大的高。

图5 不同粗糙度下定子温度随时间的变化

3.4 主轴热变形分析

将3.3节温度场计算结果作为结构载荷进行加载，并对电主轴的位移进行约束，得到电主轴系统的热变形。主轴的热变形主要包括轴向和径向热变形，取轴向热变形进行分析。

为了直观地看出主轴的轴向热变形，通过ANSYS中的路径功能，可得到主轴热变形随主轴长度变化的曲线，如图6所示。

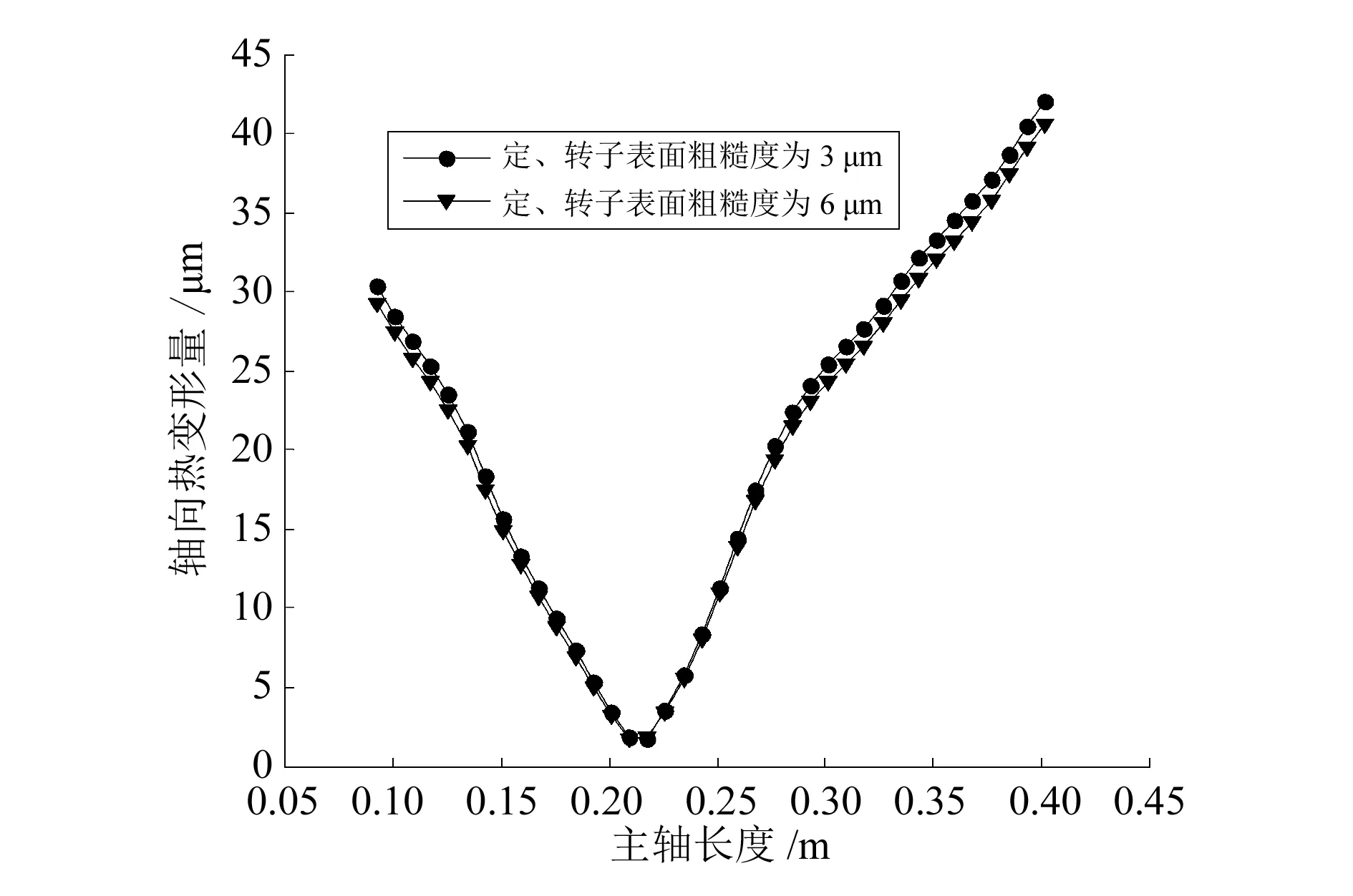
图6 不同粗糙度下轴向热变形量随主轴长度的变化

由图6可知，最大变形量出现在主轴两端，转子芯部变形最小。原因是主轴定、转子生热及前、后轴承生热造成的热变形逐渐向两端累积而成，其热变形越大对加工精度影响就会越大。同时可看出，定、转子表面粗糙度为3 μm时，最大变形为42.002 μm；而粗糙度为6 μm时，最大变形为40.589 μm，下降了3.48%。这是因为随着定、转子表面粗糙度的增加，定、转子间隙换热系数不断升高，热交换进行得更充分，对外散热较快，降低了变形量。

4 结论

本文在考虑定、转子表面粗糙度的情况下，采用有限元方法对电主轴进行了热态特性分析，得到以下结论：

1)电主轴高速运转时，其摩擦损耗较大，变得不可忽略，因此在研究电主轴生热量时应考虑空气摩擦引起的损耗。

2)随着定、转子表面粗糙度的增加，定、转子间隙换热系数不断增加，使得定、转子产生的热量得到更好的扩散，降低了主轴的最高温升，最大热变形量随之减小。

3)定、转子表面粗糙度对空气摩擦损耗和定、转子间隙换热系数均有影响，但换热系数对温升的影响更大。