基于力学与数学的机械设计难点易化研究

刘 庆，尹晓丽,，李春明，李万腾，刘 晓，孙 凤，曹 惠

(1.中国石油大学(华东)中国石油大学胜利学院，山东 东营 257061) (2.中国石油大学(华东)机电工程学院，山东 青岛 266580) (3.山东大学机械工程学院，山东 济南 250061)

在机械设计[1]学科确定之初，力学和数学尚未完善和普及，一些知识点的表述缺乏力学和数学基础，导致理解难度高，初学者必须将其当成基本概念而死记硬背。比如一些计算公式是直接给出的，没有推导过程，因而成为难懂的知识点。这些高难度知识点阻碍了学科的发展与普及。

为降低机械设计诸多知识点的理解难度，需要补充师生均易忽略的力学和数学基础及分析步骤。目前，STEM(science科学, technology技术, engineering工程, mathematics数学)教学理念已成为各学科的研究热点。基于该理念，也应补充机械设计学科的数学和力学基础。

1 螺纹连结力与强度的难点易化

1)“联”指抽象的，“接”指连在一起可动，而“连”指具体的，“结”指不可动地合并，因此多个零件合成一个构件应为“连结”，两个构件相连应为“连接”。原来的“螺纹联接”，应改为“螺纹连结”。

2)螺母扳拧力学模型的建立。根据运动和受力特点，将螺母与螺杆的相对运动简化为滑块在斜面上的上升和下降运动，并以滑块为研究对象进行受力分析。分析支承力和摩擦力的关系式应补充矢量的平行四边形法则及正交分解与合成方法。假设螺母相对于螺杆做匀速旋动，根据螺母所受外力及牛顿第二定律列出力的矢量方程。计算拧紧和放松时的驱动力矩，需补充力矩M的矢量定义：

M=l×F

(1)

式中：l为从转动中心到力作用线垂足的矢量；F为力矢量。

在平面当中研究受力，所有的力矩均垂直于该平面，只有正负之分，因而可作为标量进行运算，在数值上等于力乘以力臂。

3)用矢量方程图解法求取未知量时需补充矢量等式的几何意义。在分析各矢量的大小和方向后，等号两边的矢量分别首尾相接，如果两者的起点相同，则终点重合。该特点与矢量的连接顺序无关。

4)计算轴向力所作的功时需补充功的定义。功是标量，位移是螺母的轴向移动距离，而不是路程。求螺旋升角的最大值时应补充函数的极值条件及复合三角函数求导公式。计算螺旋转动一圈的输入功[2]时应补充转矩T所作功W的定义：力矩与转动角度的乘积。W在数值上为：

W=T2π=Fr2π=FC

(2)

T=r×F

(3)

T=rF=Fr

(4)

式中：整体传动角度上的转矩T与零件受力角度上的扭矩在数值上相等，与施力角度上的力矩M也在数值上相等；F为产生力矩的力；r为力作用点所在螺母上圆的半径；C为该圆的周长；黑斜体符号为相应的矢量。

5)对于具有自锁功能的螺纹，证明效率η小于50%时需补充不等式成立的条件。

(5)

式中：ψ为螺纹升角；ρ′为接触面的当量摩擦角。

第一个不等式成立的依据为分母增大则分式减小。

(6)

第二个不等式成立的依据为螺纹连结的自锁条件：

ψ<ρ′

(7)

也可根据式(7)及半角公式证明：

(8)

6)当铰制孔螺栓连结或铆结承受横向载荷时，螺杆或铆钉杆受到挤压。需补充：当被挤压面为圆柱面时，有效挤压面积为实际接触面在直径平面上的投影面积；螺栓或铆钉杆在受力面积上可视为均匀受力，压强可作为正应力，力除以剪切面积可作为切应力。

7)受横向工作载荷的紧螺栓连结会受到摩擦力矩的作用，需补充：转矩T作用下转动零件所受的切应力计算式。用于起吊重物的松螺栓连结需考虑冲击的影响。如忽略冲击，则设计的设备容易损伤。因此，必须增大安全系数、载荷系数或螺栓直径。

8)细长螺杆受较大轴向压力时，存在失效[3]的可能。目前除临界载荷之外尚无其他设计依据。该依据来源于压杆失效。原来，该失效与受轴向压力转轴失去自动定心能力的失稳相混淆，定义为压杆失稳。该定义误导了研究方向，导致避免该类失效的设计准则尚无成熟理论。如果以失效的机理为研究目标则更有希望获得进展。

9)螺栓连结的强度计算需采用试算法。许用应力随螺栓尺寸的变化而有所变化。因此，设计时，先假设螺栓尺寸来确定许用应力并计算最大应力，再比较两者的大小。如果最大应力大于或远小于许用应力，则修改螺栓尺寸并重复上述步骤。螺栓既受到正应力又受到切应力，需用当量应力设计尺寸或校核强度。因此，需补充零件设计常用的第三强度理论(最大切应力理论)和第四强度理论(形状改变比能理论)[4]。

2 传动部件的难点易化

(9)

(10)

式中：W为所作的功；t为时间；F为所受的力；s为力方向上发生的位移；r为转动中心到F的垂直距离；n为转速。

如果所有变量均采用国际单位制，则很多公式的常数不再出现，且更便于理解。

2)设计软齿面中心距时需采用模数、齿数和螺旋角的试算值，然后再校核试算的模数是否满足弯曲强度要求。如果校核结果为不满足，则需要依次调整这3个参数。

轮齿之间是点线接触，计算齿面疲劳应力时需补充赫兹公式。该式根据应力定义及变形特点推导而来，但是未介绍推导过程。理解各符号含义即可用于教材上尚未介绍的齿轮齿条传动、凸轮传动等的接触应力计算。计算轮齿弯曲应力时需补充弯曲疲劳应力计算公式、危险界面的弯曲截面系数、30°危险截面等材料力学知识点。

3)分析带受力的步骤为：建立坐标系—取微带—沿切向和法向分别分析所有受力，根据牛顿第二定律获得方程组。计算带的应力分布时需补充力的叠加原理，即各力单独作用结果之和与共同作用的结果相同。一般情况下，机械上的力学系统都是线性系统。求压轴力(作用在带轮轴上的力)时需补充正弦定理和余弦定理。可由几何关系获得方程，需要特别注意的是带传动紧边和松边的拉力不相等的情况。带传递的功率可表示为拉力与带速乘积的形式，该定义推导式为：

(11)

4)推导挠性体摩擦的欧拉公式[5]时需补充重要极限、二阶近似式、对数函数及其求导方法。带传动的离心惯性力FC的计算需利用：

(12)

式中：x为变量；α为带轮的包角。

带由两段线段和两段圆弧组成，在求带长时，需要使用该极限(见式12)，同时还要使用有限项无穷阶近似级数(泰勒级数)的近似公式：

(13)

式中：f(·)为函数；x0为当前点。

5)悬垂的链在传动方向、竖直方向、横向上均存在周期性变化的速度分量。分析链传动的多边形效应需要补充振动力学[6-7]的简谐振动。此外还需根据相对运动建模。

6)凸轮轮廓线的反转法设计需补充相对运动原理[8]。如果令纸作匀速转动，令从动件按给定规律运动，则两构件接触点在纸上留下凸轮轮廓线，但是实现难度很高。如令整个机构反转，而纸保持不变，则易实现绘图。

刚化反转法是在确定结构尺寸时常用的机构设计方法。将多个设计条件分别绘在纸上，根据已知构件将多张纸重合，则可将给定连架杆位置的设计转化为给定连杆位置的设计。

在机械加工中，刀具与工件通过相对运动完成复杂的加工。当转动的刀具刚度不足时，可令工件转动，完成相同的切削任务。复杂的加工面可由刀具和工件同时运动而获得。

7)周转轮系的转化轮系需基于相对运动建立。针对实际啮合情况，标注各体的假定转动方向，基于啮合关系建立转速与齿轮齿数之间的关系式。对于图1所示的机构，标注系杆的转动方向，系杆指向纸外的运动会造成齿轮2转速变慢或反转，因此齿轮2上向左标注系杆的转动方向可与齿轮3上向下标注相一致。根据啮合关系，可列出参考计算式：

(14)

(15)

式中：i为传动比；ω为角速度；z为齿数；数字下标为齿轮序号；下标H为系杆代号；上标H表示相对于系杆。如果由方程组或方程求得某体转速为负值，则其实际转动方向与假定方向相反。

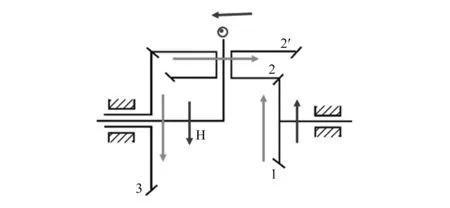
图1 标注方向的周转轮系

3 轴系部件的难点易化

1)轴上多个键槽布置原表述为：布置在同一母线上。一个形状布置在一条线上，难以确定位置。因此，该表述改为：为了加工方便，同一轴上的多个键槽，必须与经过轴线的同一个平面对称，并且宽度应尽量相同。

2)轴承支反力在经典著作上只提供了需死记硬背的计算式。理论上，在轴线所在的平面内，轴系没有转动，但是仍满足刚体的力矩平衡方程，基于此可推导计算式。计算角接触轴承的轴向力时，应明确轴承外圈为研究对象。轴的强度校核和刚度校核完全是一道力学应用题，需补充并强调材料力学的弯矩、扭矩、强度理论、叠加原理、挠度、转角、扭角等知识点[9]。这类综合运用多个力学和数学知识点的过程，只要有一处需要死记硬背，该过程的难度就陡然提升。

3)滑动轴承的工作过程应补充流体动压理论。根据形成动压的条件，可分析其启动过程的3个阶段。滑动轴承压力场与温度场的计算均需要另一个场已知，先假设一个温度场，计算出压力场之后，再计算温度场。该结果必然与假设值不同，修正之后，重新计算压力场。多物理场交替求解[10]，直到修正量足够小为止。

4)万向连轴器主动-从动轴的速比关系式推导过程需补充：动坐标系与静坐标系之间的坐标转换矩阵、三角函数求导公式、三角函数代换公式和矢量运算法则等。基于坐标系转换和矢量运算的推导结果[5]相同，二者之间相互验证。

令主动轴转角为φ1、从动轴转角为φ3、两轴夹角为β，则该速比关系式为：

(16)

4 结束语

机械设计是以高等数学、材料力学和弹性力学等为基础的专业学科，概念及理论体系必须具有连续性和交叉性。这种不同学科知识点之间的联系普遍存在，如：从蝙蝠吃肉到超声波应用，从二分法悖论到盲人探路及半步优化方法，从排列组合理论到穷举机构法等。

术语的命名如符合汉语语义则更易懂易学，否则凭空增加了知识点。从语言学角度重新审视基本概念是有必要的。目前，力学和数学知识足够普及，机械设计学科除定义外，任何死记硬背的知识点都能转化为可理解的导出概念。本文针对高难度知识点所补充的力学和数学基础，以及所提出的创新点，均有利于机械设计学科的发展。