一种锚杆锚固长度无损检测物理滤波技术的数值模拟

张建业,李青锋

(湖南科技大学 资源环境与安全工程学院,湖南 湘潭 411201;湖南科技大学 矿业工程研究院,湖南 湘潭 411201)

锚杆支护作为巷道的主要支护形式,其施工质量具有一定的隐蔽性,许多冒顶事故的直接原因是锚固参数未满足设计要求,利用应力波无损动力检测锚杆长度、锚固长度等参数,可以为锚杆施工质量提供保障,但在现场的检测工作中常面临长度检测精度低等问题[1-2],如反射位置识别错误、反射信号不明显.因此,本文为提高锚杆锚固长度参数的检测精度设计了一种物理滤波方法,并通过数值模拟的手段分析该方法的可行性.

1 应力波在锚杆中的纵向传播规律分析

图1a为普遍应用于煤矿锚杆支护中的树脂锚杆,锚杆杆体长度为L,其中锚固段长为L1,在托盘处由螺母对锚杆施加预紧力P.预紧力作用下托盘使围岩产生明显的挤压变形,所以将锚杆外端边界简化为一端弹性支承，则图1a所示锚固锚杆的模型可简化为外端弹性支承、锚固段与锚固剂黏结的纵向振动力学模型,如图1b所示.

图1 树脂锚杆纵向振动力学模型

对于如图1b所示的锚杆纵向振动力学模型,设杆长为L，锚固段长为L1,密度为ρ,截面积为A,弹性模量为E.沿x轴线上锚固段杆体周围的分布力为X(x).假定杆的横截面在振动中始终保持为平面,忽略因杆的纵向伸缩而引起的横向变形,即同一截面上各点仅在x方向产生相等的位移,则图1b所示力学模型可以看作如图2所示的均质等截面细直杆.以u(x,t)表示杆上距原点x处在t时刻的纵向位移.在杆上取微元段dx,其受力如图3.根据牛顿第二定律,它的运动方程为

图2 杆纵向振动

(1)

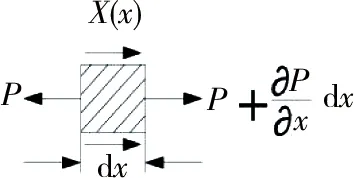
图3 杆上微元段受力

(2)

将式(2)代入式(1)并化简,得

(3)

或

(4)

其中

(5)

可见杆的纵向振动的运动微分方程也是一维波动方程,由于分布力X(x)的复杂性,式(4)的求解需要通过数值分析方法求得[3].

2 应力波在锚杆中的衰减规律分析

应力波在锚固系统传播过程中的衰减可分为空间衰减和时间衰减,轴向各点的幅值因传播距离的增加而减小称为空间衰减，每一点的幅值随周期增加而减小称为时间衰减[4].应力波的衰减可归因于几何因素和物理因素[5],几何因素包括波阵面的扩展和应力波在交界面的反射、折射等，物理因素为锚杆体系的非完全弹性、热传导等[6].本文通过分析由物理因素所导致的应力波在锚固锚杆中的衰减规律完成滤波目的.

2.1 应力波的时域衰减规律

地震学中,在一个周期中质元所消耗的能量ΔE与原有能量E的比值被称为品质因子Q,品质因子被用来表示介质对应力波的吸收特性,表达式为[7-8]

(6)

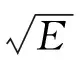
(7)

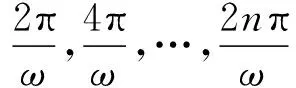
(8)

可得

(9)

所以

(10)

A(t)=A0exp-αt.

(11)

可得空间衰减因子Qt：

(12)

2.2 应力波的空间衰减规律

应力波沿锚杆的传播随着传播距离的增加,轴向各截面幅值A将发生衰减.令一个波长λ内振幅A的变化为ΔA,根据波长与频率关系可知：

(13)

(14)

式中:c为应力波在介质中得传播速度.

将式(14)代入式(7)可知：

(15)

求解可得

A(x)=A0e-ωx/2cQ.

(16)

A(x)=A0e-βx.

(17)

可得空间衰减因子Qs:

(18)

通过以上分析可得知,时域衰减因子Qt与空间衰减因子Qs，时域衰减系数α与空间衰减系数β之间存在关系如下:

Qt=Qs;

(19)

(20)

实际检测工作中,无法直接对服役锚杆的不同截面进行信号检测,但可以通过检测服役锚杆底端反射信号的幅值计算时域衰减系数,再通过式(20)将时域衰减系数转换为空间衰减系数.

3 含有辅助检测杆的锚杆锚固长度参数检测数值模拟

在检测现场,锚固锚杆外露段长度通常是不同的,导致在外露端局部段反射的信号周期不同，锚杆外露端截面因磨损、腐蚀等原因与传感器耦合程度低,检测工作前需要对外露端截面进行打磨.因此,设计一种辅助检测杆,通过辅助检测杆内螺纹调节使不同长度的锚杆外露段为定长,保证待测锚杆反射周期一致，同时辅助检测杆端面可以提高与传感器的耦合程度,提高检测效率.

3.1 含辅助检测杆的锚固预应力模型的建立

参考煤矿常用的锚杆锚固系统参数,利用FLAC3D建立初始模型,其中,锚孔深1.8 m,直径0.03 m;锚杆长1.95 m,直径0.02 m;锚固介质长0.5 m,厚0.01 m;螺母长0.025 m,内径0.02 m,外径0.03 m;托盘尺寸:0.095 m×0.005 m×0.095 m,内径0.026 m;围岩尺寸:0.4 m×1.8 m×0.6 m;辅助检测杆长0.1 m,直径0.04 m;托盘与围岩壁间建立了接触面;自辅助检测杆外露端面至围岩壁的距离为0.18 m.锚固模型建立完成后随即对锚固系统施加50 kN的预应力.

锚固系统初始模型如图4,锚固介质模型如图5,锚杆轴向受力如图6,托盘与围岩接触面如图7,各部分力学参数如表1.

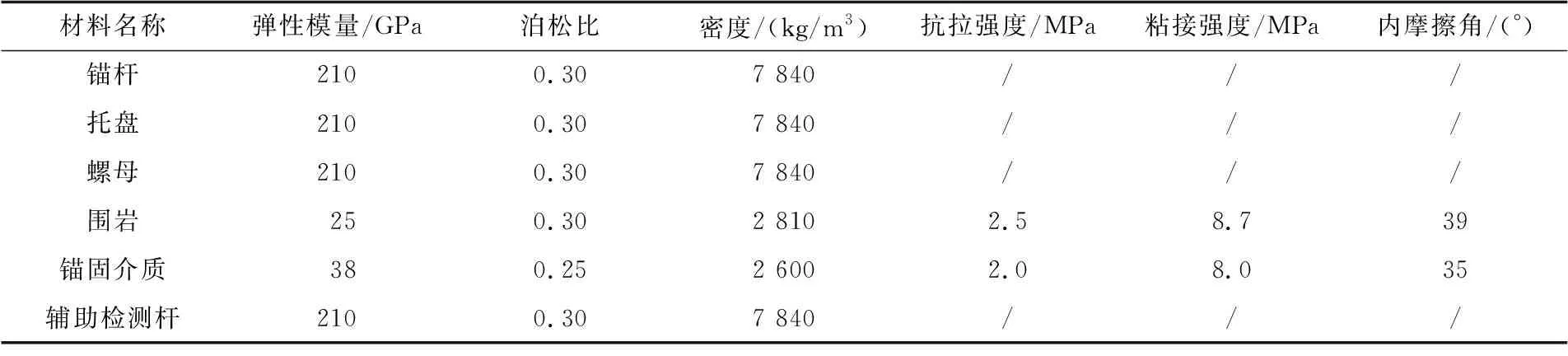
表1 锚固系统各部分力学参数

图4 含辅助检测杆的初始模型

图5 锚固介质模型

图6 预应力下锚杆受力云图

图7 托盘与围岩间接触面模型

3.2 锚固长度动测数值模拟

在桩基检测中,激振力作用时间主要受锤头材质影响,锤头越硬,质量越轻,荷载作用时间越短;反之,锤头越软,质量越重,荷载作用时间越长[9].激振力通常采用半正弦波来模拟,但半正弦波的一阶导数不连续[10].为此,本文采用式(21)模拟,即

(21)

式中:p(t)为激振力;t0为激振作用时间.

本文激振作用时间为60 μs,利用上述激发条件,激振辅助检测杆端面的中心位置,同时对辅助检测杆端面纵向振动速度的时域信号进行监测,根据围岩壁的反射信号确定反射周期(0.000 209 s),激振力如图8,整体检测结果如图9.

图8 模拟激振力

图9 锚固系统整体检测信号

3.3 纵向应力波在锚固系统中的波速分析

锚杆锚固长度参数的检测工作中,确定应力波在锚固段和非锚固段中的纵向传播速度尤为重要.通过式(5)计算理论波速,纵向应力波在非锚固段理论传播速度为5 175 m/s，纵向应力波在锚固段理论传播速度为4 819 m/s.

通过检测锚固段和非锚固段上等间距各点纵向振动速度的时域信号幅值,确定数值模拟中非锚固段的纵向波速c1=5 200 m/s,锚固段纵波波速c2=4 761 m/s.非锚固段部分点时域幅值信号如图10,锚固段部分点时域幅值信号如图11.

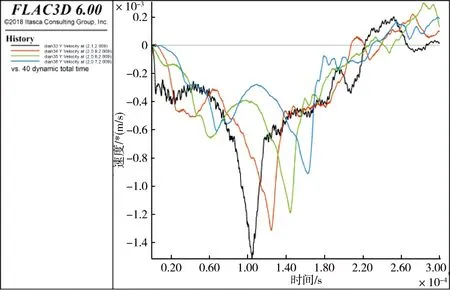
图10 非锚固段幅值监测

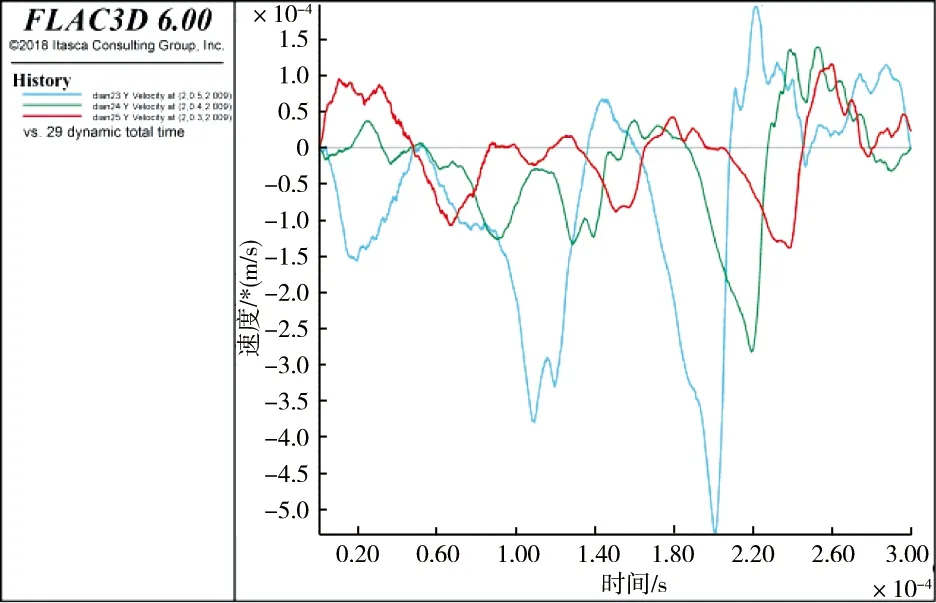
图11 锚固段幅值监测

4 非锚固段衰减拟合与检测信号的物理滤波

锚固锚杆的非锚固段和锚固段可以抽象为交界面两侧截面尺寸不同的连续杆,交界面附近两侧的位移、速度和力连续,但材料参数不连续.由交界面两侧材料的不连续性可知,应力波在非锚固段和锚固段的传播过程将产生不同程度的衰减,通过检测非锚固段上多个等间距点的时域信号幅值拟合应力波在非锚固段的时域衰减规律.利用辅助检测杆确定检测信号的反射周期,取一个周期的非锚固段反射信号代入应力波在非锚固段的衰减规律中,近似得到仅含非锚固段反射的滤波信号.将滤波信号与外露端检测得到的整体反射信号对比整合,完成物理滤波.

利用数值模拟手段,对非锚固段上等间距的不同截面进行检测,根据不同截面的时域幅值信号直接拟合得到应力波在非锚固段的时域衰减系数.

4.1 非锚固段衰减规律拟合

在锚固长度动测模拟过程中，检测非锚固段上多个等间距点的轴向振动速度信号,对每个点时域信号的幅值数据用最小二乘法进行拟合,得到本文中的纵向应力波在预应力锚固系统的非锚固段时域衰减规律,如图12所示.

图12 非锚固段衰减拟合曲线

根据前述对应力波在锚杆中的衰减分析,对应力波在非锚固段中的衰减进行拟合.拟合结果中R2为决定系数的平方,决定系数的值在0～1变化,R2接近1,说明拟合效果好.根据拟合结果,确定本文纵向应力波沿非锚固段传播t秒后,沿非锚固段传播的衰减与时间的关系为

v=v0e-9 750t.

(22)

式中:v0为非锚固段上某点纵向振动速度幅值;t为波的传播时间.

4.2 物理滤波

假设锚杆杆体中只存在一个交界面,那么检测过程中外露端将接收到一个明显的反射信号,然而完整的锚固系统包含多个交界面,两个交界面之间可以假设为具有某一厚度的层,位于层中的波将要经受多次反射与透射,使应力波能量产生衰减,随着透射波传播至新的交界面,新交界面的反射信号便会被层中的反射信号所干扰.在锚固长度检测工作中,如果可以拟合得到应力波在非锚固段这一“层状”结构中的反射信号作为滤波信号,那么作为新交界面的锚固起始位置和结束位置的反射将更加容易判断.

数值模拟检测过程中,通过来自围岩壁的反射信号确定反射信号周期约为0.000 140 5 s.取非锚固段反射周期信号数据并对振动速度数据取绝对值如图13;将处理后的数据代入式(22)中对非锚固段反射信号进行拟合并作为滤波信号,如图14;将检测得到的整体的数据取绝对值后与滤波信号进行整合,如图15.

图13 反射周期信号绝对值处理

图14 滤波信号

图15 滤波后的结果

由图15可知,在规律的波形中可以看到明显的起跳信号与起跳后的衰减,根据锚固段起始反射信号与入射信号反相,锚固段结束反射信号与入射信号同相,可以清楚地判断锚固起始位置反射时间为0.000 57 s,锚固结束位置反射时间为0.000 80 s.根据前述,可以确定非锚固段长度为1.48 m(模型中非锚固段长度为1.46 m),锚固段长度为0.54 m(模型中锚固段长度为0.5 m).

5 结论

1)依据应力波衰减规律,实验和模拟验证了应力波沿锚杆传播时呈负指数衰减，推算了预应力锚杆非锚固段的时域衰减系数.

2)辅助检测杆的设置为锚固长度参数无损检测提供了一种物理滤波方法,通过理论计算验证了数值模拟过程的准确性.辅助检测杆的设计尺寸应依据激振力作用时间而确定.

3)检测工作中可以利用辅助检测杆调节锚杆外露段长度为定值,从而确定反射信号周期,删减来自围岩处第一次反射产生的干扰波,使信号分析更准确.