混合非参数回归的贝叶斯推断

李道扬, 何幼桦

(上海大学理学院, 上海 200444)

混合回归模型是研究在样本服从的总体分布是不同分布混合时, 解释变量与被解释变量关系的统计模型, 由Goldfeld 等[1]在1973 年提出. 之后, 很多学者对混合回归的问题展开了研究. Wedel 等[2]于1995 年将混合线性回归模型推广到混合广义线性回归模型; 1999 年,Gaffney 等[3]使用期望最大化(expectation maximisation, EM)算法解决了混合回归中的一般参数估计问题; Song 等[4]在2014 年提出了基于拉普拉斯分布的混合稳健回归模型等. 对于混合非参数回归问题, 也有一些学者进行了研究. Huang 等[5]在2013 年使用基于样本局部似然函数的EM 算法解决了混合非参数回归问题; Wu 等[6]在2016 年提出了基于半参数模型的混合分位数回归模型; 胡烨[7]于2017 年在混合泊松回归模型的基础上进一步研究了半参数混合泊松回归的问题等. 在混合回归模型的应用方面, Fraley 等[8]在1998 年将混合回归模型应用于糖尿病患者与健康人的分类和密度估计问题; Gaffney 等[3]于1999 年将混合回归模型应用于视频中的动作识别问题等.

本工作针对一般的混合非参数回归问题, 给出了一种基于贝叶斯框架的方法. 首先, 对回归中的每个非参数混合成分用一个随机过程的有限维分布族作为先验, 同时分别构造混合比例、随机误差的方差和非参数混合成分的贝叶斯估计, 并通过马尔科夫链蒙特卡洛(Markov chain Monte Carlo, MCMC)法抽样来进行后验推断; 然后, 通过数值模拟来分析混合非参数回归模型的贝叶斯推断方法的有效性; 最后, 应用该推断方法解决了蚜虫数量与受感染烟草植物数量关系的实际问题.

1 混合非参数回归的贝叶斯估计

考虑有K个非参数回归的混合, 回归的解释变量为x, 被解释变量为y, 第k个非参数混合成分gk(x)的比例为αk, 满足αk ∈[0,1],αk= 1,随机误差εk ～N(0,σ2k),则混合非参数回归模型(以概率αk产生)为

在混合非参数回归问题中, 对任意给定的x, 需要给出其每一个混合成分下回归的估计值k(x)、混合比例的估计值k以及随机误差εk方差的估计值.

混合非参数回归模型中被解释变量y的分布函数一般为

式中:Φ(u) 为标准正态分布的分布函数, 记标准正态分布的概率密度函数为φ(u);g(x) =(g1(x),g2(x),··· ,gK(x)),α= (α1,α2,··· ,αK),σ= (σ1,σ2,··· ,σK). 在本模型中, 假定gk(x) 是非参数的, 而αk和εk与x无关. 如果gk(x) 是线性模型, 那么模型(1) 就退化为Goldfeld 等[1]提出的混合线性模型, 也就是说, 本工作中的混合非参数回归模型是混合线性回归模型中的线性回归在非参数回归上的一种推广.

设{(xi,yi),i= 1,2,··· ,n}是总体的一组随机样本,U= (xn+1,xn+2,··· ,xn+t)′是待预测点的向量. 记X=(x1,x2,··· ,xn)′,Y=(y1,y2,··· ,yn)′,T=[X′,U′]′. 那么可以得到样本的联合密度:

式中:φσk(u)=).

在本工作中, 引入中间变量zik来简化式(2)的复杂度. 如果第i个样本(xi,yi)属于第k类, 那么就记zik=1; 否则zik=0, 也就是说zik ∈{0,1}, 且有

记z=(zik)n×K, 则样本的联合密度函数可化简为

为了构造非参数成分gk(x)、混合比例αk和随机误差方差σ2k的贝叶斯估计, 需要分别给定其先验分布. 由于gk(x)是一个函数, 因此其先验需要使用一个随机过程的有限维分布族来刻画. 假设其服从高斯过程GP(gk0(·),·), 由于只关心gk(x)在T上的估计, 因此gk(x)在T上的先验只需用高斯过程的有限维分布来描述, 即N(gk0(T),τ-1Σk), 其中Σk是阶数为(n+t) 的协方差矩阵,τ是衡量先验分布信任程度的超参数; 考虑到混合比例αk的先验需满足αk0∈[0,1],αk0= 1, 取Dirichlet 分布作为混合比例联合密度的先验; 对于随机扰动的方差, 则将参数为θk和βk的逆伽马分布作为其先验, 即

式中:τ,g10(T),g20(T),··· ,gK0(T),Σ1,Σ2,··· ,ΣK,α10,α9,··· ,αK0,θ1,θ2,··· ,θK,β1,β2,··· ,βK均为先验超参数.

定理 在先验满足式(3)～(5) 的情况下, 关于α,gk(T)和σk的后验分布则有如下结论.

结论1gk(T)|g-k,α,σ,z,X,Y,T ～N(μ*,Σ*),k=1,2,··· ,K, 其中

结论2α|z,g,σ,X,Y,T ～Dirichlet(α*), 其中

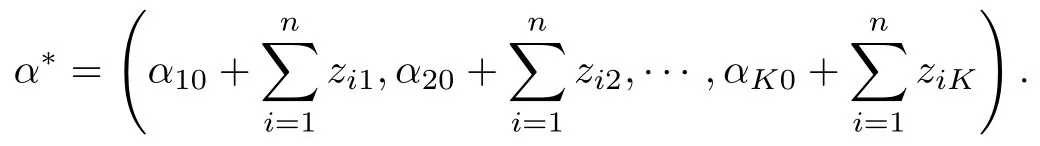
结论3σ2k|z,g,α,σ,X,Y,T ～IG(σ2k;θ*k,β*k),k=1,2,··· ,K, 其中

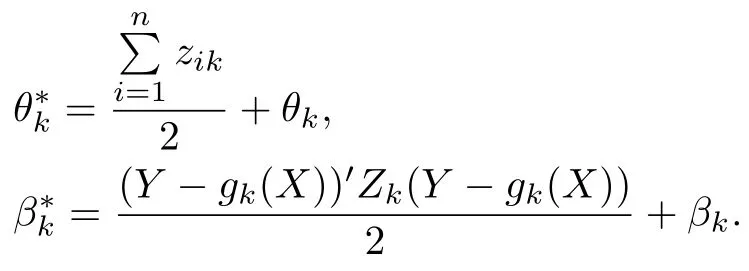
证明 根据贝叶斯定理可以得到各个参数的联合后验分布.

式中:g=(g1(T),g2(T),··· ,gK(T));Zk=diag(zik),i=1,2,··· ,n,k=1,2,··· ,K.

根据联合密度函数可以得到在给定其他参数的情况下gk(T)的后验分布:

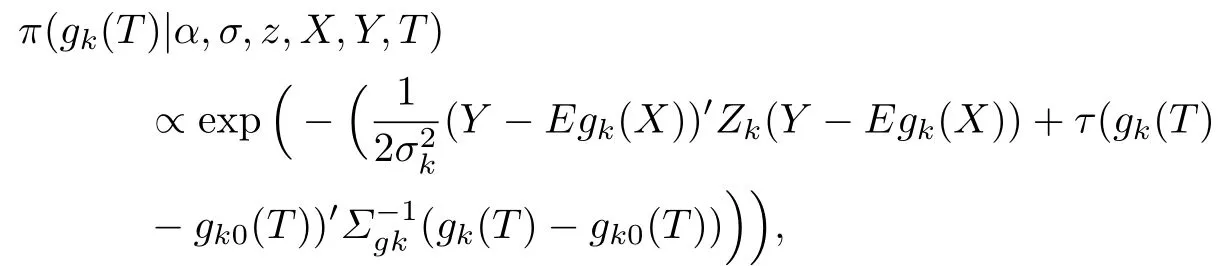
引入辅助矩阵E=[In×n On×t], 那么上式可化简为

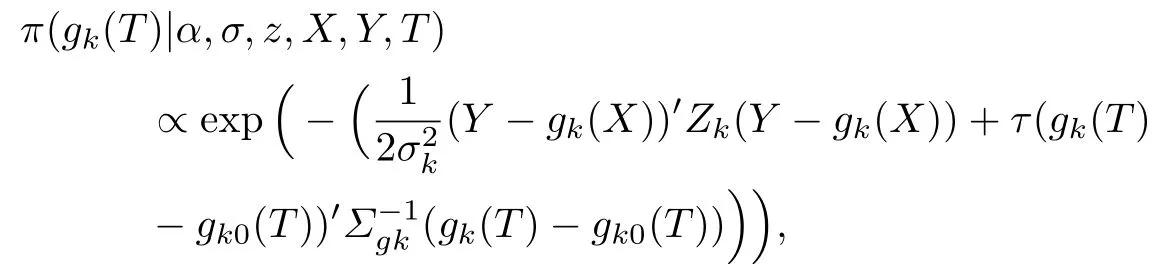
整理可得

结论1 得证.

同理对α可以得到后验分布:

从而α|z,g,σ,X,Y,T服从参数为α*的Dirichlet 分布. 结论2 得证.

同样对于σ可以计算后验分布:

于是,π(|z,g,α,X,Y,T)～IG(),k=1,2,··· ,K, 其中

结论3 得证.

从定理中可以得出,g,α,σ的后验分布均是结合先验信息和样本信息的结果. 特别地, 对于具体的gk(T), 其后验分布的均值可以看作先验信息与样本信息的加权平均, 也就是说, 在同样的样本信息的情况下, 较好的先验分布能得到更准确的后验估计.

由于联合后验分布的密度函数的结构较为复杂, 因此使用MCMC 方法中Gibbs 抽样分别得到g,α,σ的后验分布. 利用Gibbs 抽样构造MCMC 链的关键在于分别得到g,α,σ的满条件分布, 然后根据满条件分布依次轮换抽样得到相应的马氏链. 而马氏链的平稳性, 使得把这些链的实现作为样本来推断所需的联合分布得以实现. 结合定理的结果, 可以得到各参数满条件分布, 从而给出MCMC 抽样算法.

(1) 设定先验分布的超参数τ,g10(T),g20(T),··· ,gK0(T),Σ1,Σ2,··· ,ΣK,α10,α20,··· ,αK0,θ1,θ2, ··· ,θK,β1,β2,··· ,βK和g,α,σ的初值g(0),α(0),σ(0), 以及MCMC 抽样次数.

(2) 抽样第j步, 根据P(zik= 1|g(j-1),α(j-1),σ(j-1),X,Y) 分别计算zik= 1 的后验概率pik,k= 1,2,··· ,K,服从参数为(pi1,pi2,··· ,piK) 的多项分布, 即从～Multinomial(pi1,pi2,··· ,piK)抽取,i=1,2,··· ,n.

(3)根据gk(T)的满条件分布π(gk(T)|,X,Y,T)抽取(T), 其中g-k=(g1(T),g2(T),··· ,gk-1(T),gk+1(T),··· ,gK(T)),k=1,2,··· ,K.

(4) 根据α的满条件分布π(α|z(j),g(j),σ(j-1),X,Y,T)抽取α(j).

(5) 对σ2k, 根据满条件分布π(σ2k|z(j),g(j),α(j),X,Y,T)抽取σ2(j)k ,k=1,2,··· ,K.

(6) 重复(2)～(5), 直至完成预设的抽样次数.

2 数值模拟

本工作通过讨论混合非参数回归模型的贝叶斯推断方法在不同情况下的表现, 以验证该方法的有效性. 下面分别从样本量大小、各类回归线的相对位置以及多种混合成分的情况这3 个角度来讨论此推断方法的效果. 为了更加直观地显示贝叶斯推断方法的有效性, 采用Xiang[9]在2018 年提出的全局期望最大化(global EM, GEM)算法作为对照方法. GEM 算法是一种用于处理混合半参数混合回归问题的改进类EM 算法, 同样适合处理混合非参数回归问题.

2.1 样本量不同的情况

这里, 主要讨论考察样本量大小对贝叶斯推断方法估计精度的影响, 并与对照方法作比较. 为此, 本工作采取了一种2 个成分混合的模型, 考虑到产生样本的模型需要一定的波动性来反映贝叶斯推断方法和对照方法的拟合能力, 故采用如下方式设置产生样本:

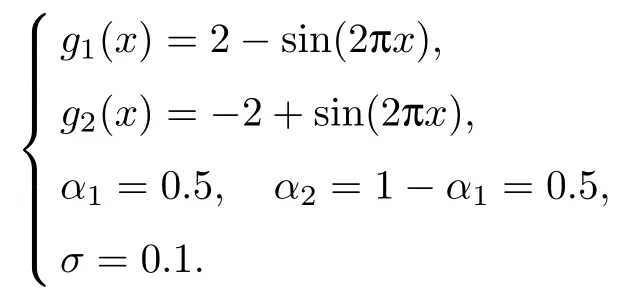
为了更直观地比较贝叶斯推断方法和对照方法的精度, 本工作采用平均根误差(square root of the average squared error, RASE)作为衡量估计精度的指标:

式中:xn+i,i= 1,2,··· ,t为待预测样本点;N为实验的重复次数;(xi)为第l次实验中gk(xi)的估计值. 采用均方根误差(root of mean square error, RMSE)作为衡量混合比例α和随机误差项ε方差σ2的估计精度指标:

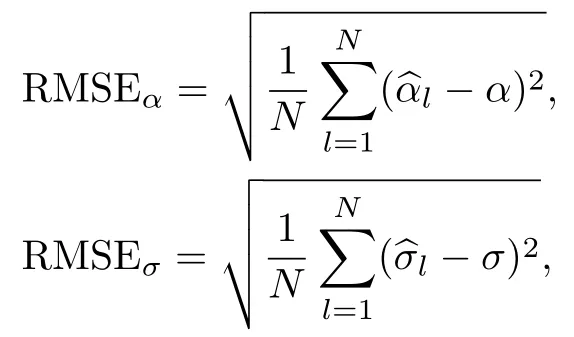
式中:,分别为第l次实验中α,σ的估计值. 在贝叶斯推断方法中, 采用后验均值作为回归和参数的估计值. 在贝叶斯推断方法中设置先验及超参数:

式中:g10(x) =(2;g20(x) )=-2;τ-1= 0.1;α10= 0.5;α20= 0.5;σ0= 0.1;θ=-1.5;β=0;(Σ)ij=exp;h为经验带宽.

本工作使用贝叶斯推断方法和GEM 算法分别在样本量n= 50,100,150,500 时计算100个预测点的结果, 并对各种情况重复100 次实验, 计算预测点的误差结果如表1 所示.

表1 样本量不同情况下的估计误差Table 1 Estimation error in different sample sizes

观察表1, 可以得到2 个结论: ①随着样本量的增加, 贝叶斯推断方法和GEM 算法的精度都得到了提高; ②对比贝叶斯推断方法和GEM 算法的结果可知, 在对α的估计方面, 贝叶斯推断方法略好于GEM 算法. 而在回归的精度和对σ的估计方面, 贝叶斯推断方法显著优于GEM 算法, 这表明贝叶斯推断方法能够利用先验信息来增强模型的拟合和预测能力, 并且贝叶斯推断方法即使在样本量不大的情况下, 也能得到较为精确的结果

2.2 各类回归线的相对位置

下面考察在各类回归线的不同相对位置情况下混合非参数回归的贝叶斯推断方法的表现. 当样本的类间距离较大时, 这类问题较容易解决, 因此本工作着重考虑类间距离较小时的情况.

当得到如图1(a)所示的样本时, 2 条回归线的形状存在2 种可能: ①混合成分之间存在交叉的情况; ②2 个混合成分在x= 0 处几乎相切但未交叉. 为讨论上述情况下模型的表现, 应用贝叶斯推断方法和GEM 算法下的所得结果如图1(c)～(d)所示.

此时, GEM 算法的混合非参数回归只能得到一种情况, 即默认曲线不交叉. 而通过贝叶斯推断方法可以结合先验信息对模型有一个初步判断, 并通过先验反映到模型上, 这样贝叶斯推断方法就可以根据不同的具体情况拟合2 种形状(见图1(c), (d)), 这一点是传统的类EM 方法不能做到的. 从这个角度看, 贝叶斯推断方法能够满足更一般的情况, 这也是贝叶斯推断方法显著的优势.

图1 样本及不同方法下的回归Fig.1 Sample and regression in different methods

从回归的结果看, GEM 算法对样本的拟合程度不高, 尤其是在两侧样本边缘处, 这也是非参数模型的共性问题; 而在贝叶斯推断方法的结果中, 无论是取交叉的先验还是不交叉的先验, 总体回归效果较好, 这说明贝叶斯推断方法能够在样本较少的地方结合先验信息来优化回归的结果, 这从侧面印证了贝叶斯推断方法的精度要高于GEM 算法的结论.

2.3 多种混合成分的情况

以3 种混合成分问题为例, 验证模型在多种混合成分情况下的有效性(见图2). 为测试贝叶斯推断方法和GEM 算法在复杂情况下的适应性样本分别由线性函数、三角函数和二次函数产生, 然后混合而成, 其实验结果如图2 所示. 图2 中的样本从上至下分别由线性函数、三角函数、二次函数产生.

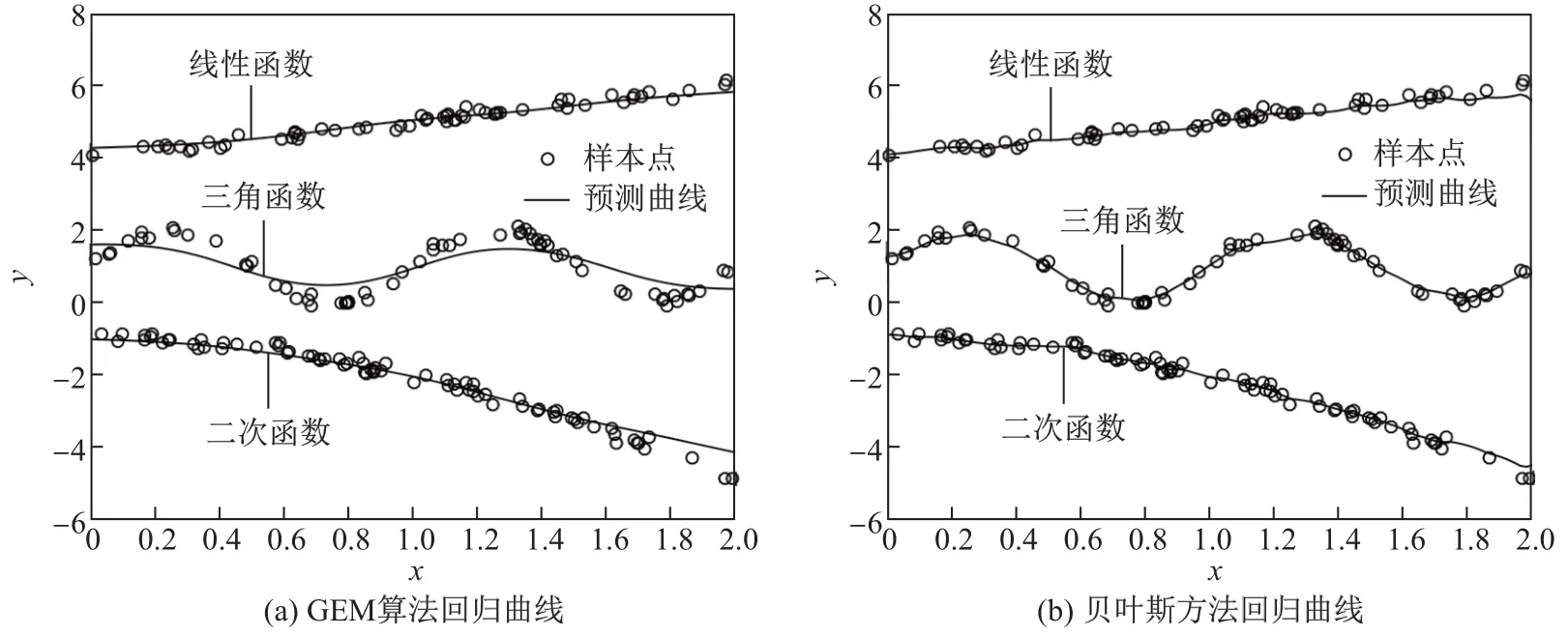
图2 3 种非参数混合成分下的回归Fig.2 Mixtures of three nonparametric regressions

从图2 中可以看出, 2 种方法都能处理多种成分混合回归问题, 而不是仅限于2 种混合成分的非参数回归问题. 在波动性较强的回归曲线中, GEM方法的表现较差, 因为传统的非参数方法只能通过核函数加权利用附近点的样本信息; 而贝叶斯推断方法不仅可以利用样本信息,还可以结合先验信息, 这就使得贝叶斯方法具有更强的拟合和预测能力. 对本例来说, 给定的先验信息只包含了3 条曲线的区分度信息, 而并未包含曲线的形状和趋势信息. 结果表明, 即便如此贝叶斯推断方法也能得到较好的结果.

3 实证分析

Boiteau 等[10]给出了一个关于蚜虫和感染烟草植物关系的生物学实验数据, 该数据包含51 个独立实验的结果. 在每个实验环境中设置12 株感染烟草植物和69 株健康烟草植物, 并在环境中释放不同数量的蚜虫. 在每组实验进行24 h 后, 检测先前健康植物的感染情况并记录受感染的植物数量. 所记录的释放蚜虫数量与受感染植物数量样本散点图如图3(a)所示.

随着蚜虫数量的增加, 感染植物的数量与其不是单纯的正向相关, 而是围绕在2 条回归线周围. 其中一条随着蚜虫数量的增加而增加, 且增长速度明显大于线性增长; 另一条受感染烟草植物数量极少, 且对蚜虫数量的增加并不敏感. 这种情况是传统的一条回归曲线所不能处理的, 需要用到混合回归. Boiteau 等[10]使用了混合线性回归来处理此问题, 拟合结果并不理想;Gr¨un 等[11]在2008 年用混合广义线性回归来拟合结果, 所得结果有一定的改进, 但因其对模型做了预设使得模型不具有一般性.

使用混合非参数回归的贝叶斯推断方法结果如图3(b)所示. 模型同时估计了混合比例和随机误差的标准差的后验均值. 在位于上方的曲线中, 混合比例α1的后验均值为0.621 5, 标准差σ1为5.412 0; 在位于下方的曲线中, 混合比例α2的后验均值为0.378 5, 标准差σ2为1.111 5. 总的来说, 在所有样本中约有62%的样本围绕上方的曲线波动, 此时感染植物的数量随蚜虫数量增加而增长较快, 随机误差的方差也较大; 在大约有38%的样本中, 受感染植物的数量几乎没有, 且与释放蚜虫数量的关系并不明显, 随机误差的方差也较小. 可见这2 条回归线表明此推断方法可以较好地捕捉样本的性质和结构.

图3 蚜虫数量与受感染植物数量的关系Fig.3 Relationship between the number of aphids and the number of infected plants

4 结束语

本工作基于贝叶斯的框架给出了一种混合非参数回归的统计推断方法. 首先, 分别给出非参数成分gk(x)、混合比例αk以及随机误差的方差σ2k的先验分布(其中对非参数成分gk(x)的先验以一个随机过程的有限维分布族的形式给出); 然后, 引入中间变量来简化样本的联合密度函数; 最后, 结合先验信息和样本信息给出后验分布. 数值结果表明, 由于混合非参数回归的贝叶斯推断方法能够利用先验信息, 故在适应性、一般性和精度上都优于GEM 算法, 并且即使在小样本的情况下也能得到较为精确的结果. 最后蚜虫数量与受感染植物数量关系的实证分析表明, 混合非参数回归的贝叶斯推断方法能够同时有效地处理聚类与回归问题, 且方法更具一般性.