一种确定活性炭滤盒源中碘活度分布的方法
柯链宝,夏 文,叶宏生,宋鑫鹏,徐利军,林 敏,陈克胜
(1.中国原子能科学研究院 计量测试部,北京 102413;2.中国原子能科学研究院 计量与校准技术重点实验室,北京 102413)
I-131是一种人工放射性核素,是核设施的气态流出物之一,也是其中重要的检测对象[1]。目前对I-131的检测主要通过检测仪对气体中的I-131进行收集,测量一定体积下的放射性碘的活度值。因此对于碘检测仪的校准极为重要。由于I-131的半衰期仅有8.02 d,常用长寿命的Ba-133源代替[2]。而目前主要方法是通过Ba-133源与I-131源的传递因子K将探测效率进行传递,一方面可以达到保存时间长的优点,又避免了直接使用Ba-133源所带来的13%的误差[3]。但影响仪器校准准确性的因素不仅如此,由于源距离探测器的距离会直接影响探测器的探测效率,因此用于仪器校准的校准标准源分布所造成的偏差,也是影响其准确性的因素之一。因此确定标准源中I-131的分布情况能够为开展仪器校准工作提供帮助。
不同形态的碘在活性碳中分布情况略有不同,例如无机碘(I2)在活性炭中由于吸附效率高,通常呈现平面分布(表面吸附的体源);有机碘(CH3I)在活性炭中吸附效率低于无机碘,其分布常呈现指数分布[4];当出现高浓度长时间的吸附时,活性炭中的吸附位被填满,则会出现均匀源的情况。由于不同分布的碘源得到的探测效率会产生差异,因此在利用均匀分布的Ba-133源进行量值传递的过程中,不同分布的碘源对于传递因子K的影响不同。因此需要对不同源的分布情况进行分析。
1 实验部分
1.1 主要仪器与装置
低本底高纯锗γ谱仪:美国Ortec公司,相对效率66%,对60Co能量点为1.33 MeV的能量分辨率为1.9 keV;全自动样本处理系统:型号SF6,中国上海永创医疗器械有限公司。
1.2 主要材料与试剂
活性炭滤盒:HI-Q公司,TC-45型TEDA浸渍活性炭滤盒;浸渍活性炭:TEDA,20~40目,HI-Q公司;Na131I标准溶液:利用符合测量装置进行绝对测量定值;三个待测活性炭滤盒I-131源。
1.3 实验方法
1.3.1利用点样器制备均匀分布的I-131平面源 设置点样器操作参数,参数信息列于表1,利用定好活度的Na131I标准溶液滴在已经裁剪好的滤纸上,将滴好的滤纸平面标准源进行塑封,塑封后裁剪至滤盒内径的尺寸。

表1 点样器操作参数信息
1.3.2效率深度曲线的测量 在确定一个活性炭滤盒中I-131的分布前,需要确定探测器对I-131探测效率与I-131所在深度的关系以及不同碳层厚度的自吸收影响。具体方法是通过控制同一平面标准源在活性炭滤盒中的不同深度进行实验探究,平面源下的碳层厚度利用电子天平对活性炭进行质量控制。为了避免探测器污染,设定该活性炭盒与探测器之间依靠塑料架支撑,如图1所示。
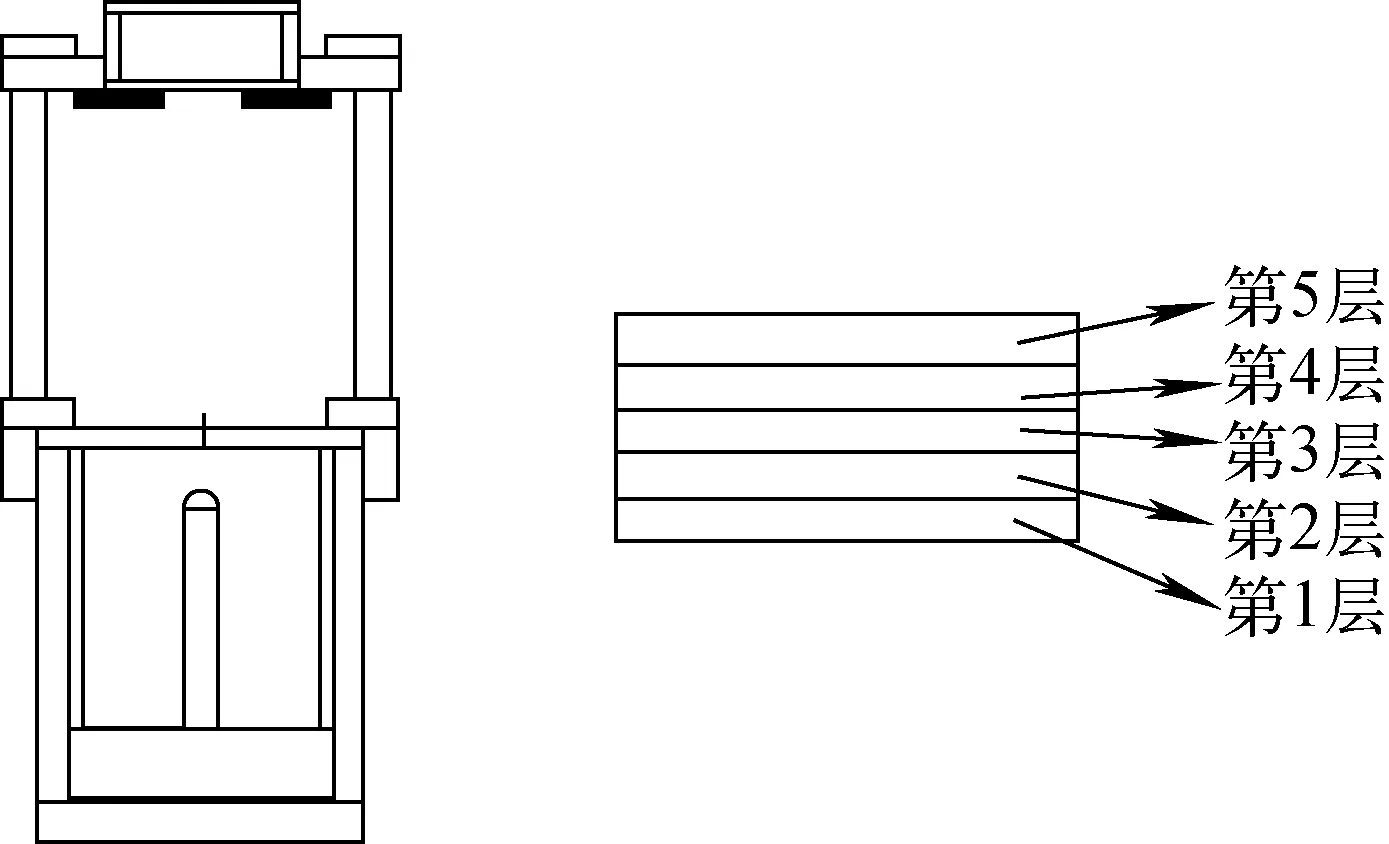
图1 高纯锗γ镨仪测量活性炭滤盒模型
将活性炭滤盒中的活性炭一共分为5层[5],取0、4.8、8.8、12.8、16.8以及20.4六个点位,共5层,分别是[0,4.8)、[4.8,8.8)、[8.8,12.8)、[12.8,16.8)以及[16.8,20.4]。
通过多次测量确定一般活性炭盒中活性炭的质量,平均质量为26.08 g,根据活性炭的平均值推算出每层的活性炭质量以及累积质量,并称量出实际质量。活性炭滤盒内高度为20.4 mm,每1 mm的活性炭质量为1.278 g。每层活性炭质量和累积活性炭质量,如表2所示。

表2 活性炭质量确定
将制备好的平面源依次置于6个位点,设定塑料架高10 cm(高纯锗探头距离活性炭滤盒的距离),进行测量,结果修正到第一次测量前。
利用MCNP进行模拟验证比较,探测器晶体参数如表3所示。
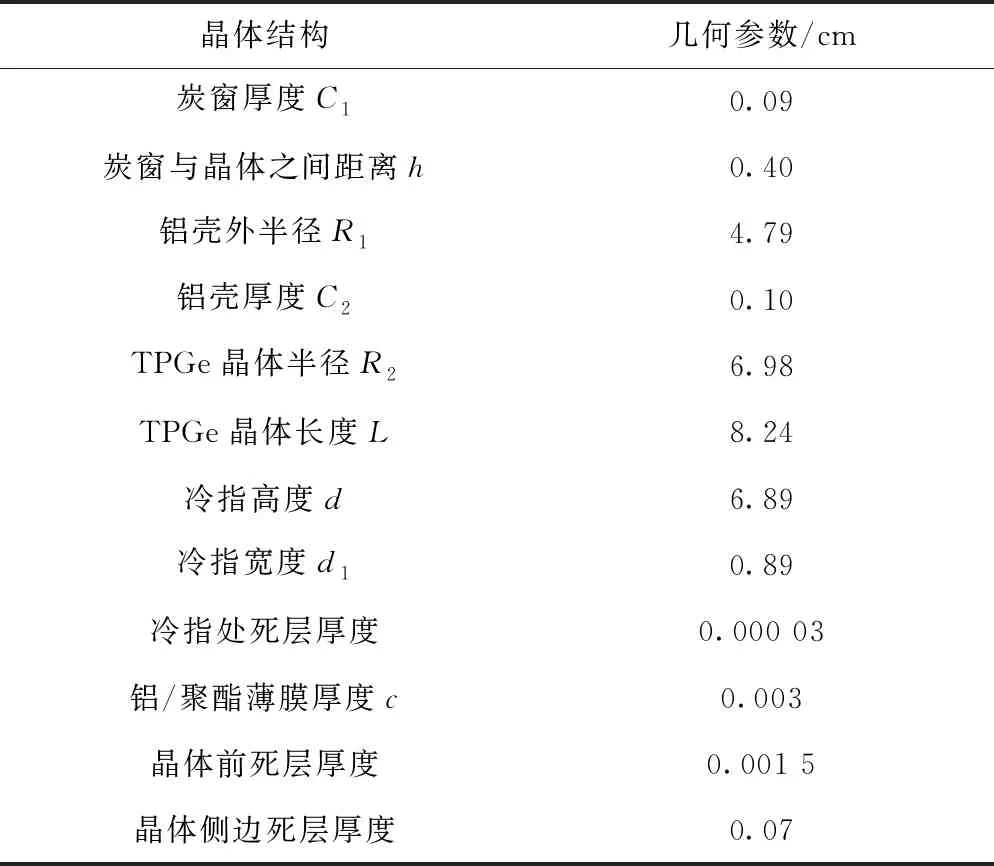
表3 探测器晶体参数
1.3.3分布函数的计算 将待测的活性炭碘盒置于塑料架上,利用高纯锗γ谱仪进行测量定值;将其反置于塑料架上,重新进行测量定值。
2 结果与讨论
2.1 I-131放射源分布的可能性
目前主要的体源分布形态有三种,均匀源、平面源(表面吸附的体源)以及指数源分布,其中均匀源和平面源分布仅有一种情况,指数源分布则有四种情况,如图2所示。

a——表面未吸附饱和且放射性碘未穿透活性炭滤盒;b——表面吸附饱和但放射性碘未穿透活性炭滤盒;c——表面未吸附饱和但放射性碘穿透活性炭滤盒;d——表面吸附饱和且放射性碘穿透活性炭滤盒
图2中的四种指数源以及面源和均匀源等六种情况均可能在实际操作中出现。实际检测器在进行检测时,探头对碳盒中不同深度的放射性碘的响应除了与该处的活度大小有关,还与其在该位置的探测效率有关。在不考虑测量时间产生的衰变,探测器的净计数率满足:

(1)
式中,A(x)为活性炭滤盒中放射性元素的活度分布函数;η(x)为活性炭滤盒中不同深度的探测效率;x为活性炭滤盒中的深度位置,x∈[0,20.4],mm。
对于不同分布的源,其在活性炭滤盒中的分布函数不同。
1) 均匀源的分布最为简单,其分布函数为:
A(x)=C,x∈[0,20.4]
(2)
式中,C为常数。
基于均匀源的分布函数,其正反两面分别进行测量,经过衰变修正,得到数值理论上相等。
2) 平面源(表面吸附的体源)分布,最先接触气流的一面为活度最高的一面,其余均未有活度,因此其分布函数为:
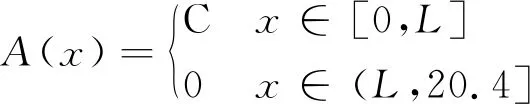
(3)
式中,L为平面源厚度,mm。
3) 指数源分布,根据图2的a)~d)四种情况可以分别归纳出其分布函数为:
(4)
式中,C、n、m、s为参数;L1为平面层厚度,mm;L2为空白层厚度,mm。
对于未被放射性源穿透的a)和b)两种情况,其参数n值为0,放射性穿透的c)和d)则有参数L2值为20.4;对于表面未饱和吸附的a)和c)两种情况,其参数L1值为0。
事实上,均匀源与平面源(表面吸附的体源)可以看作是指数分布源的特例。

对于平面源,是指数分布中s趋近于无限大的情况,(n+mesx)则趋近于单层活性炭的饱和吸附值,在活性炭本身均匀的情况下,可以认为其值为常数。实际制备过程中,即使活性炭对无机碘的吸附能力强,单层的活性炭对气体中的碘吸附率仍小于100%,因此,实际制备的无机碘源满足特殊情况的指数分布源。
2.2 效率深度曲线的确定
根据实验条件,将平面源分别置于0、4.8、8.8、12.8、16.8以及20.4六个点位进行测量,得到计数,与活度值进行比对即可得到相应点位的探测效率。利用MCNP对活性炭进行模拟得到的效率结果如图3所示。
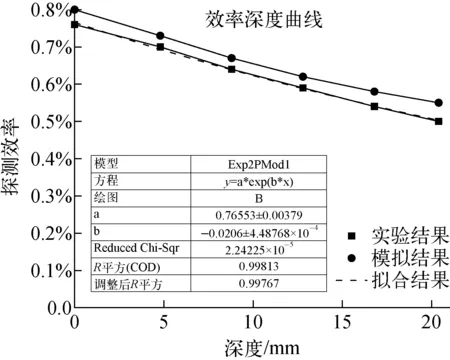
图3 效率深度曲线
拟合结果深度-探测效率关系为:
η(x)=0.007 655 e-0.020 6x
(5)
式中,x为活性炭滤盒内部深度,x∈[0,20.4],mm。
此拟合结果仅适用于本台高纯锗γ谱仪测量置于10 cm塑料架的I-131源,且碘源储存于活性炭滤盒(HI-Q公司,TC-45型TEDA浸渍)。利用相同方法进行实验求解可以得到其他仪器或源的深度-探测效率关系。
模拟结果明显高于实验结果,原因在于实际操作条件,活性炭铺层无法达到理想状态,会高于理想模型,因此实验结果低于模拟结果。
2.3 分布函数的求解
在测量过程中I-131会发生衰变,导致计数率下降,因此需要对计数率进行衰变修正,本文不对修正进行讨论,因此给定的计数率均为修正后的净计数率,修正时间为第一次测量开始时。
根据图1将函数分为5个区间,[0,4.8)、[4.8,8.8)、[8.8,12.8)、[12.8,16.8)以及[16.8,20.4]。以每个区间的中点为取值点,此时函数关系式可以转化为:
(6)
式中,n1为正方向(活度大的一面靠近探头)净计数率,已进行衰变修正;i为放射源所在层数,i=1,2,3,4,5;Ai为第i层放射源活度,Bq;ηi为第i层的探测效率。
第i层的探测效率ηi的值为区间起始点的探测效率值与区间终点的探测效率值的均值,因此可以分别算出每层的探测效率值,如表4所示。

表4 探测效率与层数
拟合结果与实际实验均值偏差小于3%,可以利用拟合结果估算实际的探测效率值。
反向探测效率随深度的函数η(x)未发生变化,其活度分布发生翻转且位移了长度L的距离,因此将活性炭滤盒翻转180°后重新进行测量,其函数关系式应为:

(7)
式中,n-1为反方向(活度小的一面靠近探头)净计数率,已进行衰变修正。
同样将原本的五层区间[0,4.8)、[4.8,8.8)、[8.8,12.8)、[12.8,16.8)以及[16.8,20.4]倒置,则总的函数图像面积即为总计数为:
(8)
式中,η′i为倒置区间的探测效率。
根据效率深度曲线拟合结果,将倒置的五个区间数据代入,得到倒置区间中值的探测效率,如表5所示。
2) 由于第五层活性炭层薄,仅有3.6 mm,因此倒置时其中值位置较正置炭盒低(后续炭层亦如此),更接近探测器,另一方面炭层薄自吸收小,因此其各区间中值位置的探测效率相较于正置区间高。
整理公式(6)(8)可得:
(9)
式(9)中单层的活度值Ai的表达式只需将深度x利用区间(Di,1,Di,2)中值代入即可求解:
Ai=A(x)×(Di,2-Di,1)
(10)
式中,i为区间标号,i=1,2,3,4,5;x为区间(Di,1,Di,2)的中位数;A(x)为活性炭滤盒第i层区间(Di,1,Di,2)的中位数x处的活度值,函数表达式为式(4)。
将每层区间中值x代入单层的活度关系式(10),得到式(11):
(11)
并将式(11)代入式(9),迭代求解式(9)可以得到参数n、m和s的结果。
将三个待测样进行正反测量,将测量结果代入,结果如表6所示。

表6 待测样分布求解结果
当活性炭碘盒属于均匀源时,其正反偏差小于0.1%,在实际测量过程中可以忽略该误差,认为正反测量结果相等,因此能够直接通过正反测量结果进行判定;当活性炭碘盒属于平面源(表面吸附的体源)时,正反偏差极大,达到50%以上;当活性炭碘盒属于指数源时,其偏差介于均匀源以及平面源(表面吸附的体源)之间。但无法通过正反测量结果的比较直接判断待测源属于指数源或者平面源(表面吸附的体源)。
得到三个待测样的活度分布函数,代入不同的区间范围,得到不同区间的活度分布情况,如表7所示。

表7 各区间及相应活度值

图4 不同分布的活度-深度曲线
不同区间的活度分布情况表明,均匀分布源活度数值与深度无关,而指数分布源与平面分布源则呈现出一定的变化规律,不同区间内的活度呈递减趋势,指数分布源活度主要集中于1、2、3三个区间,平面分布源其活度主要集中在第1区间。
根据待测源各区间平均活度求解结果,确定各区间的活度,绘制活度曲线,确定其分布情况,利用表7中区间的活度数据进行活度-深度曲线的绘制,得到图4所示的结果。
求解的过程将区间中值的函数结果认为是该区间内放射性碘的平均活度,但该区间的范围内,碘的活度并不是完全均匀,存在由大到小的渐变趋势,所得出的拟合结果也仅是一种渐变情况,不能完全符合实际的分布情况。
2.4 确定实际分布情况的方法
由于利用正反测量结果所解得的结果为可能分布的情况之一,因此可以通过限定条件对其函数进行限制。方法主要有两种,一种通过限定表面的最大吸附,另一种是通过测量活性炭碘盒的活度总量。
对于限定表面最大吸附的方法,由于在活性炭目数限定的条件下,单位质量活性炭的吸附量存在一个极大值,因此对于活度分布函数,其指数部分存在极大值的限定,其主要解决的对象是图2中的b)和d)两种情况,其中包括了平面分布(表面吸附的体源)。
对于活度总量的测量,其实验操作为:称量碘盒质量,打开碘盒,将碘盒中的活性炭中的活性炭摇匀,重新填充封装,称量第二次质量,进行质量修正。将经过均匀化处理的活性炭滤盒进行测量。
经物理手段将活性炭均匀化处理,原本的指数分布转变为均匀分布,再次利用高纯锗γ谱仪进行定值。基于均匀分布的函数关系式以及深度探测效率的拟合结果,可以确定总活度的关系式为:
(12)
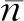
将公式(6)(8)(12)进行整理,可得:
(13)
代入活度分布函数A(x),可以求解出活度分布函数的三个参数。由于对活性炭的饱和吸附等条件进行限制,此时确定的分布函数更加吻合实际分布。
3 结论
任何一个含放射性的样品其分布是复杂的,直接与其制备条件有关,I-131的放射性样品主要有三种分布情况,平面分布、指数分布以及均匀分布。根据理论分析,均匀分布源与平面分布源属于特殊条件的指数分布源,在求解分布的过程中,均以指数分布源的求解方式进行处理,然后根据各区间活度绘制活度分布情况。理论上,将I-131的测试盒进行微分,在准确测得I-131深度效率曲线的情况下,可以通过迭代求解正反计数得到准确的源分布。结合绘制结果,得出均匀分布的I-131源正反测量结果偏差最小(0.062 5%),平面分布的I-131源(表面吸附的体源)正反测量结果偏差最大(51.0%),指数分布的I-131源正反测量结果介于均匀分布与平面分布之间(40.6%)。
在已知样品分布可能性的条件下,对样品具体的分布函数进行求解,主要用于研究在高精度测量条件下,不同制备条件所导致的样品微量分布的不均匀性,对现场校准过程中的校准标准源的制备工作提供帮助。

