基于扩散卡尔曼滤波算法的目标跟踪估计

程 华 张雪婷 房一泉

(华东理工大学信息科学与工程学院 上海 200237)

0 引 言

以往关于目标跟踪的研究大多专注于采用集中式算法，这些集中式算法常常运行在静态多传感器平台上[1-3]，而集中式卡尔曼(Kalman)滤波在传统的目标跟踪算法中又起到了至关重要的作用。对目标状态估计的性能在很大程度上依赖于所采用的协作跟踪算法。在集中式解决方案中，全部传感器节点将其测量值转发到一个数据融合中心，采用传统的Kalman滤波来得到最佳状态估计，然后又将全局估计值发送回每个传感器节点。显然，这种策略需要消耗大量的能量和通信资源[4]，而且依赖中心节点及与之通信的可靠性；为此，人们又提出了分布式协作跟踪算法，这种策略之所以成为一种很有吸引力的替代方案，是因为它通常需要较少的能量和通信资源，并且还允许并行处理，所以更具鲁棒性。

适用于这种分布式控制问题的算法主要是分散式Kalman滤波算法。文献[5]基于Gossip的分布式Kalman滤波算法，分别结合成对Gossip算法和广播Gossip算法提出了2种具体的基于Gossip的分布式Kalman滤波(Gossip based Distributed Kalman Filter,GDKF)实现算法，即基于成对Gossip的分布式Kalman滤波算法(Pairwise Gossip based Distributed Kalman Filter,PG-DKF)和基于广播Gossip的分布式Kalman滤波算法(Broadcast Gossip based Distributed KalmanFilter,BG-DKF)，同时给出了采用2种分布式Kalman滤波算法进行网络目标跟踪的具体实现步骤。文献[6]采用容积Kalman滤波器来处理分布式摄像机网络中的目标跟踪问题。首先将平方根容积信息滤波器进行扩展，提出了分布式平方根容积信息滤波器，使其能适应大规模网络。另外，针对摄像机网络中由于摄像机装置在一个较大的区域内，摄像机观测区域有限，目标可能会出现在观察的盲区，造成某些摄像机的测量数据无效的问题，提出了平方根容积信息加权一致性滤波器(Square-Root Cubature Information Weighted Consensus Filter,SCIWCF)对状态信息和信息矩阵加权，减小无效信息在一致性算法的作用，从而提高整体的滤波性能。仿真实验结果表明，算法能够在摄像机网络中对目标进行有效跟踪，在估计精度和滤波器稳定性等方面要优于传统的信息滤波。文献[7]基于两阶段Kalman滤波器对多传感器信息融合问题进行了研究。首先在并列集中式融合框架下，利用观测值扩维融合的思想，将各传感器的观测信息扩维为系统状态的增广观测矩阵，并构建出对应的增广观测方程。然后基于单传感器的两阶段Kalman滤波对系统状态和系统偏差进行联合估计。最后依据并列分布式融合框架，在分析各传感器局部两阶段Kalman滤波结果的基础上，利用系统状态估计误差协方差阵构建对应的加权融合系数，进而实现系统状态的全局融合估计。仿真验证了并列分布式两阶段Kalman融合滤波方法性能的优越性。文献[4]也对此问题进行了研究，但假设网络是完全连通的。文献[8-9]的研究中采用了同样的假设，但考虑了严格的量化通信情况。文献[10]提出了Kalman滤波迭代并行运行在一组传感器上。然而，该算法主要针对多处理器系统，而且仍然需要一个数据融合中心来合并估计值。文献[11]的研究采用了简化的状态空间模型，并提出了一种基于平均协商一致的聚合过程。

文献[12]针对Kalman滤波和RLS滤波之间的联系进行了研究。文献[13]把关于自适应传感器网络上的RLS研究扩展到了Kalman滤波领域。文献[14]针对在一般情况下的分布式目标跟踪问题，提出了一种基于协商一致性的Kalman滤波算法，算法需要若干平均迭代来获得估计值，但仍然要求网络是全连通的。

本文研究了一个节点网络(如传感器网络)上的分布式目标跟踪问题，提出了扩散Kalman滤波算法，目标是为每个节点估计系统的状态。首先对每个测量值和每个节点，采用来自于邻近区域的数据计算出一个局部状态估计值；然后，采用扩散步骤得到每个节点邻近区域估计值的一个局部平均。算法中节点仅与它们的邻居通信，不需要数据融合中心。仿真实验结果表明，本文算法在状态估计均方偏差性能和平均能耗方面都有很大的改进。

1 分布式Kalman滤波算法原理

1.1 Kalman滤波算法

考虑一个状态空间模型的形式为：

(1)

式中：xi∈CM和yi∈CP分别表示系统在时刻i的状态向量和测量向量；Fi、Gi、Hi为大小合适的系数矩阵；信号ni和vi分别表示状态和测量噪声，而且假设为零均值和白色的，具有协方差矩阵：

(2)

式中：E{·}表示求数学期望；*表示共轭转置；Qi和Ri分别表示时刻i的状态和测量矩阵；δij为克罗内克符号，即当i=j时，δij=1，当i≠j时，δij=0。假设初始状态x0有零均值、协方差矩阵Π0，且对于全部i，与ni和vi不相关。

测量值更新：

(3)

时间更新：

(4)

1.2 分布式Kalman滤波算法

考虑一组有N个节点在某个区域上空间分布的情形，设Nk表示节点k的闭邻域(即连接节点k且包括k自身在内的节点集合)。假设在时刻i，每个节点k根据式(1)的模型收集一个测量值yk,i∈CP如下：

yk,i=Hk,ixi+vk,ik=1,2，…,N

(5)

这一过程如图1所示。假设式(1)的模型对应于从式(5)收集全部N个测量值如下：

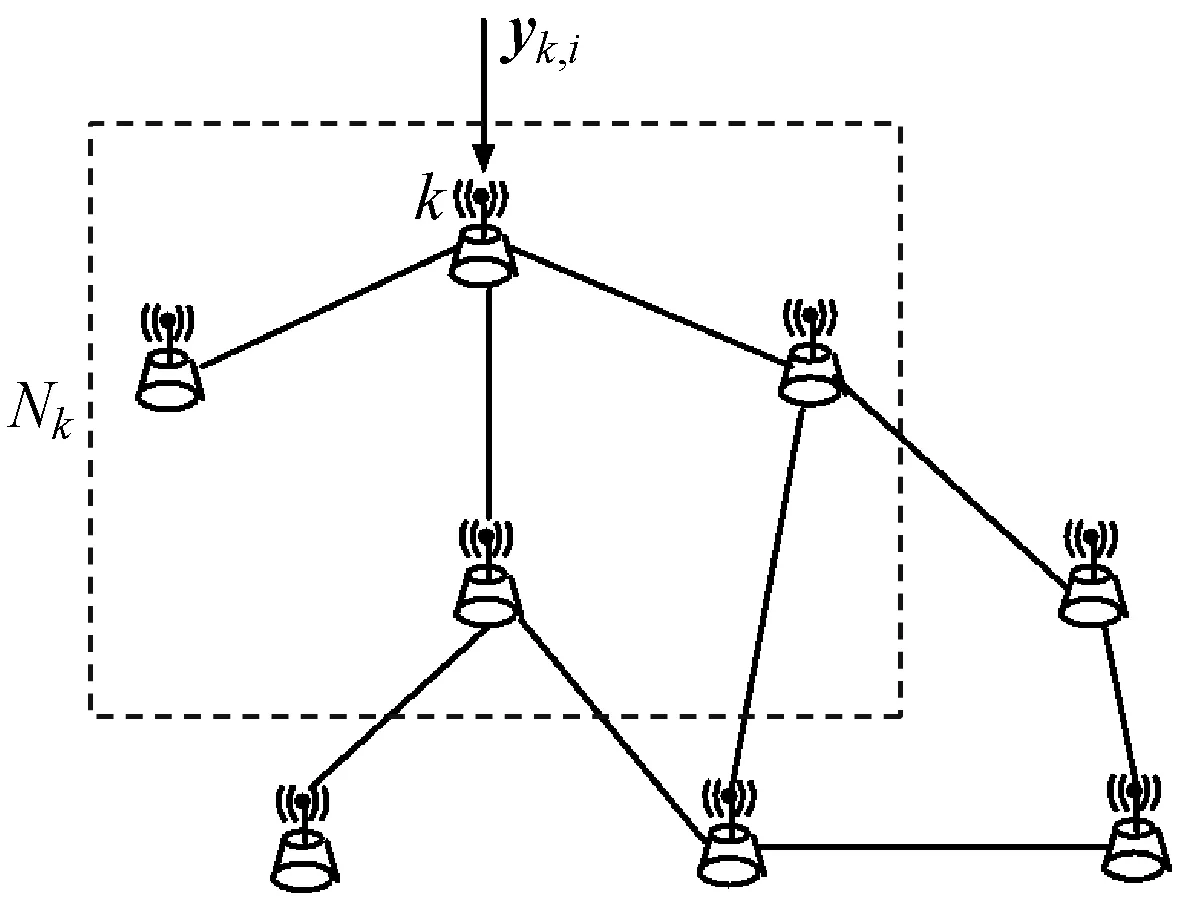
图1 每个时刻i节点k收集一个测量值yk,i

(6)

进一步假设测量噪声vk,i是空间不相关的，即：

(7)

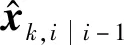
2 基于扩散Kalman滤波算法的分布式目标跟踪

2.1 局部Kalman滤波算法

为了实现扩散Kalman滤波的分布式目标跟踪，首先假设每个节点都能与它的邻居共享数据，并且仅使用来自于邻域给定的数据来获得目标状态的最佳估计，称这种估计为在节点k的邻域的局部Kalman滤波估计，它可以通过运行对于每个邻居的若干个测量值用式(3)更新来计算，其迭代伪代码如下：

Pk,i←Pk,i|i-1

forl∈Nkrepeat:

(8)

end

Pk,i|i←Pk,i

算法中箭头“←”表示按序或非并行任务。本文将式(8)称为增量步[15]，因为一个最优局部估计值是通过逐步将来自邻域的估计值和数据按顺序合并而得到的。局部Kalman滤波迭代算法仅计算每个邻域的最优估计值，而不考虑邻域的相互连接。而本文把一个扩散步骤增加到这个过程中，使得信息通过整个网络传播来显著地提高算法性能。

2.2 扩散Kalman滤波

在扩散算法实现中，节点以各向同性的方式与邻居进行通信和合作以获得比不合作情况下更好的估计值。对于自适应滤波的扩散算法如LMS和RLS已得到广泛研究[13,16]。本文遵循同样的思想来得到一种扩散Kalman滤波(Diffusion Kalman Filtering,Diff-KF)算法。

扩散KF算法及其变体需要定义一个扩散矩阵C∈RN×N，它具有以下性质：

(9)

式中：1是一个具有单位元素的N(1的列向量；cl,k是矩阵C的第(l,k)个元素。称C为扩散矩阵，是因为它控制扩散过程，并在网络的稳态性能中起着重要的作用。C中的元素表示权值，是扩散算法用于组合附近估计值的。此外，定义一个连接矩阵L如下：

(10)

根据扩散RLS算法[11-12]的并行机制，并结合局部Kalman滤波算法原理，通过在Kalman滤波更新后增加一个扩散步骤，就可以得到扩散Kalman滤波算法。这个扩散步骤就是采用邻域估计值的一个凸组合，即：

(11)

式中：ψl,i表示邻域估计矩阵。扩散步骤是通过局部节点交互通信来尝试获得全局KF性能的。可以证明，式(11)的组合是最小二乘最优的[11]。算法1为Diff-KF算法原理实现的伪代码。

算法1扩散Kalman滤波(时间和测量值更新)

Step1增量更新：

Pk,i←Pk,i|i-1

对于每个相邻节点l∈Nk，重复：

end

Step2扩散更新：

Pk,i|i←Pk,i

算法1要求在每个时刻i节点与它们的邻居节点的测量矩阵Hk,i、协方差矩阵Rk,i、增量更新测量值yk,i，以及它们的扩散更新先前估计值ψk,i通信。对于每个节点和每个测量值而言，总的通信需求是PM+M+P2/2+3P/2个标量，而且对于每个增量更新来说，它需要对一个矩阵求逆。

图2 扩散Kalman滤波算法的更新

尽管记号Pk,i|i和Pk,i|i-1已被保留，但这两个矩阵不再代表估计误差的协方差，因为扩散更新在这两个矩阵的递归式中不被考虑。

算法2扩散Kalman滤波的信息形式

Step1增量更新：

Step2扩散更新：

算法2中每个节点的每个测量值所需的总通信为M2/2+3M/2+P个标量，而且对于每个增量更新，它需要求2个矩阵的逆。算法1和算法2在数学上是等价的，会得到相同的估计结果。

算法2的增量更新类似于文献[11]中提出的更新方式，主要区别是扩散步骤。文献[11]采用基于协商一致性的方法求平均：

(12)

式中：ε为加权因子。与此相反，本文采用如式(11)的邻居的估计值的凸组合。这种差异使得本文算法的性能得到了显著提高。在文献[11]的基于平均协商一致性方法中，网络必须在达到协商一致之前执行重复的平均步骤。当这样的方法用于分布式估计时，节点更新它们的局部估计值(采用Kalman滤波或最小二乘法更新)，然后用若干迭代运行一个一致性步骤来融合估计值。在数据被融合后，采用一个新的测量值，估计值再次被更新，等等。因此，在协商一致性的估计算法中，有2个时间指标：一个是收集测量值；另一个是运行平均协商一致性。而在本文提出的Diff-KF算法中，操作是采用一个时间指标实时进行的，这样可得到更好的适应性和跟踪能力，从而提高算法的整体性能。

3 Diff-KF算法性能分析

本节分析Diff-KF算法(算法1)的平均性能和均方性能。对于每个节点，给出其均方偏差(Mean-Square Deviation,MSD)的表达式，即对于节点k为：

(13)

MSD采用时间i和节点k作为指标，是因为对于扩散算法而言，通常不同的节点会得到不同的估计值，同时，由于模型的动态性可能会随时间变化，故MSD又是时间i的函数。

(14)

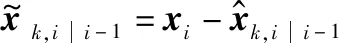
(15)

将式(14)和式(15)结合到算法2的扩散步骤中，得到：

(16)

对式(16)两边求数学期望，可以得到Diff-KF算法的估计期望值的递推式如下：

(17)

Hi=diag{H1,i,H2,i,…,HN,i}

Pi|i=diag{P1,i|i,P2,i|i,…,PN,i|i}

Pi|i-1=diag{P1,i|i-1,P2,i|i-1,…,PN,i|i-1}

同时还考虑扩展矩阵(根据式(9)和式(10))：

(18)

式中：⊗表示克罗内克积；IM为M维的单位矩阵。

现在可以用一个全局形式来表示式(16)，这个全局形式捕捉整个网络的演进：

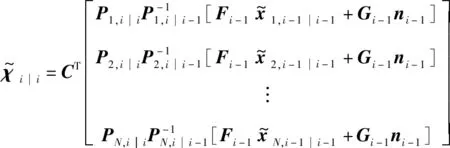
(19)

式(19)也可等价为：

(20)

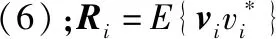
(21)

式中：

(22)

式(22)利用了克罗内克积(A⊗B)(C⊗D)=(AC)⊗(BD)的性质。

为了分析均方稳态性能，提出以下假设：

假设1模型式(1)中的矩阵是时不变的，即矩阵F、G、H、R和Q不依赖于时间i，而且F是稳定的，即它的全部特征值都在单位圆内。

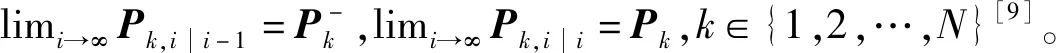
在这些假设下，矩阵Ai、Bi和Di也在稳态下收敛，且它们的稳态值如下：

(23)

假设1和假设2足以保证Diff-KF算法收敛，即式(23)中的矩阵A是稳定的，且式(22)收敛于李亚普诺夫方程的唯一解：

(24)

DRD*)

(25)

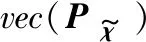
于是节点k的MSD现在可以表示为：

(26)

式中：Tr(·)表示求矩阵的迹；Ik是一个NM(NM的分块矩阵，每个块的大小为M×M，在块(k,k)位置为单位矩阵，其他地方为零。最后，整个网络上的平均MSD为：

(27)

引理1在假设1和假设2下，Diff-KF算法(算法1)是无偏且收敛的，而且每个节点的稳态均方偏差由式(26)给出。

4 算法仿真

为了评价和比较算法性能，将本文提出的Diff-KF算法与文献[11]的基于协商一致的算法、2.1节的局部Kalman滤波算法、文献[1]的集中式Kalman滤波算法的性能仿真结果进行比较。仿真中传感器网络尝试跟踪一个移动目标的位置，系统的状态就是目标的未知位置，即第一个元素和第二个元素分别是x和y坐标的一个二维向量。式(1)中的状态空间模型矩阵为：

图3 网络拓扑连接示意图

(28)

式中：|Nk|是节点k的闭邻域的基(即包括它自身在内的邻居的数目)；选择参数αk以使1×C=1*。仿真在NS2中进行。

图4为4种不同算法对于整个网络仿真得到的平均MSD(即式(18)给出的MSDave)随时间i(离散时刻)的变化关系。本文提出的Diff-KF算法在平均MSD性能方面几乎接近文献[1]的集中式Kalman滤波算法，分别优于文献[11]的基于协商一致的算法和2.1节的局部Kalman滤波算法约8.2和11.3 dB。最差的是2.1节的局部的Kalman滤波算法，因为这种算法没有扩散过程，每个节点尽管可以根据式(8)访问其邻居的数据，但每个节点都只能采用来自其邻域的数据运行传统的卡尔曼滤波。

图4 不同算法对整个网络的平均MSD随时间i的变化关系

图5为4种算法仿真得到的稳态MSD随不同网络节点数的变化关系。可以看到，本文提出的Diff-KF算法优于其余的3种分布式解决方案，仅次于集中式解决方案。这说明本文提出的Diff-KF算法是鲁棒和可扩展的。

图5 不同算法的稳态MSD随不同网络节点数的变化关系

图6为4种算法对于整个网络仿真得到的平均能耗随时间i(离散时刻)的变化关系以及平均能耗随不同网络节点数的变化关系。本文提出的Diff-KF算法尽管随着时间和节点数目的增加，能耗也会随之增加，但不如文献[11]的基于协商一致的算法和文献[1]的集中式Kalman滤波算法增加明显，因为后者或者需要全连通的网络，或需要数据融合中心。而局部Kalman滤波算法能耗增加最小，因为该算法中的每个节点仅与它的邻居共享数据，并且仅使用来自于邻域给定的数据来获得目标状态的最佳估计，而无须网络全连通和在整个网络上广播数据。

(a) 平均能耗随时间的变化关系

5 结 语

本文提出一种用于线性系统的分布式状态估计的扩散卡尔曼滤波策略。算法要求每个节点与它的邻居通信：首先共享数据，其次共享估计值。扩散过程确保信息在整个网络中传播。给出了算法的稳态均值和稳态均方分析，并通过仿真结果表明，本文提出的Diff-KF算法性能优于其他的局部式和分布式解决方案，可与最佳集中式解决方案相媲美。未来将把本文算法扩展到运动目标和摄像机网络的目标跟踪。