一种基于缓冲窗口的双哈夫曼压缩算法

乔 雨，嵇 浩

（1.南京工业大学浦江学院 计算机与通信工程学院，江苏 南京 211200；2.亚信科技（成都）有限公司，四川 成都 610000）

0 引 言

随着信息的爆炸式增长，需要传播和存储的信息量也随之增长。为了提升传播效率和节省存储空间，各种压缩文件的软件应运而生，如WinRAR等[1]。数据压缩技术可以应用在通信数据的传输、文件数据的存储、图像信息的隐藏与提取等多个领域。一般来说，整个压缩过程可能是有损压缩和无损压缩的混合，哈夫曼算法便是其中一种经典的无损压缩方法，得到了广泛的研究和应用[2]。本文对哈夫曼算法的压缩原理进行深入地研究，针对其压缩过程中存在的不足之处做出改进，进一步提升哈夫曼算法在压缩过程中的效果。

1 相关工作

1.1 哈夫曼编码算法介绍

哈夫曼编码是一种性能较优的无损数据压缩方法，在计算机科学领域，这种压缩方法被广泛用于压缩文本、图像和许多其他数据[3]。哈夫曼编码过程大致可以分为两个阶段：第一阶段先通过统计每个符号出现的概率，并将其作为符号的权重值；第二个阶段通过构造哈夫曼树，将较短的编码被分配给高概率的符号，较长的编码则分配给出现概率较低的符号。算法过程描述如下：

Step1：将每个给定的符号作为一个叶子节点，并为其确定权值；

Step2：合并两个权值最低的节点；

Step3：节点的左分支标记为代码“0”，右分支标记为代码“1”；

Step4：计算Step2中合并后两个节点的概率之和；

Step5：在树中添加另一个节点，并执行Step2～Step4；

Step6：在完成哈夫曼树的构造后，分别计算树中叶子节点的熵值、平均长度值和冗余值。

例如，有6个不同符号A、B、C、D、E、F，每个符号出现的频数见表1所列。

表1 符号频数表

将各符号出现的频数作为权值构造出如图1所示的哈夫曼树，若将树中的左分支标记为“0”，右分支标记为“1”，则该哈夫曼树中的各节点编码后的结果见表2所列。

上述的静态哈夫曼编码过程需要读取两次文件中的原始数据和权值表，存在较大的时间开销[4]。动态哈夫曼编码算法改进了静态哈夫曼编码中的不足之处，只需要在算法的第一阶段利用已编码符号的权值来构造哈夫曼树，不需要重复读取权值表。因此，动态哈夫曼编码算法的关键步骤在于如何统计所有待编码数据中符号的出现次数。由于符号出现的概率在不同的数据段中分布是不同的，并且在编码过程中会发生变化。因此，为了使算法能及时更新各符号的概率分布，文献[5]对哈夫曼编码进行改进，引入带有缓冲窗口的哈夫曼编码，来提高动态哈夫曼编码的性能。

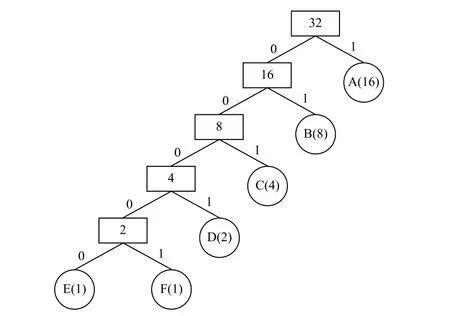
图1 哈夫曼树示例

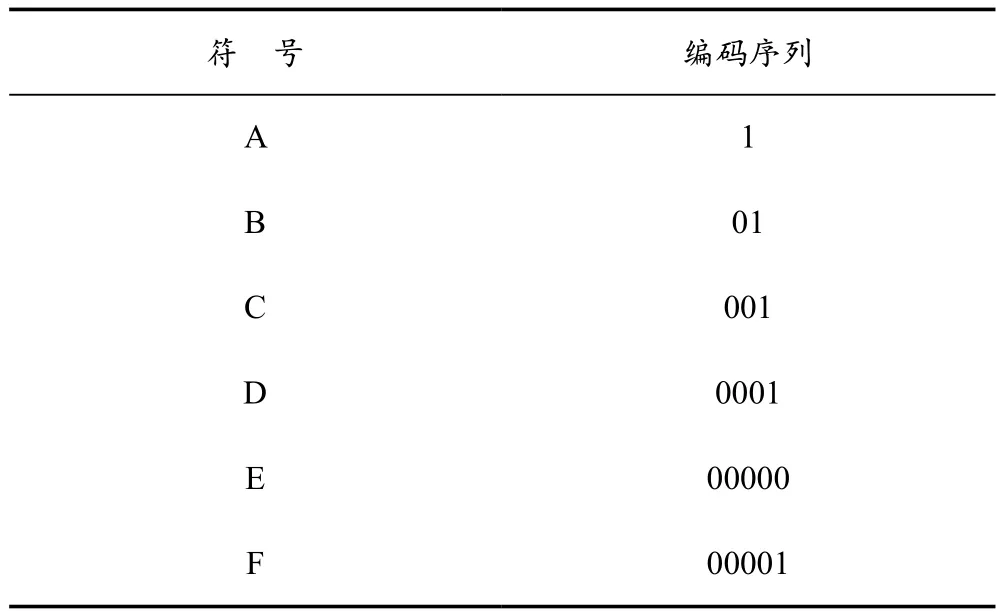
表2 符号编码表

1.2 哈夫曼编码算法研究现状

哈夫曼编码算法自1952年被提出后得到了行业内的高度关注，其在数据压缩领域的应用更是成为研究的热点。文献[6]在传统哈夫曼编码的基础上，提出一种自适应算法，该算法基于动态变化的查找表来构建哈夫曼树，进而提高哈夫曼编码算法的效率。张凤林等人提出在构建哈夫曼树的过程中利用堆排序来代替原来的排序方式，实验结果显示改进后的哈夫曼树的构建效率更高[7]。而文献[8]则是面向具体的应用系统，提出基于熵编码的哈夫曼编码改进算法，该算法利用固定奇偶码取代动态生成哈夫曼树的过程，使得编码和译码的过程更加简单，并保持可观的压缩效率。

在实际应用过程中，除了对哈夫曼编码算法本身的改进，同时衍生出了其他哈夫曼编码算法，如基于最小方差的哈夫曼编码算法[9]和基于范式的哈夫曼编码算法[10]。基于最小方差的哈夫曼算法是通过调整哈夫曼树构建过程中的中间结果的排序，使得最终的哈夫曼编码长度的方差最小。这是由于编码过程中的缓冲区大小受到编码长度的方差值的影响，方差越小，所需的缓冲区越小。因此，基于最小方差的哈夫曼编码算法能够有效降低缓冲区的空间大小，提升算法整体性能。基于范式的哈夫曼编码算法则提供一种限制编码的压缩方式，即对字符的编码均需小于或者等于设置的最大编码长度，相应的解码过程根据特定的编码方式进行解码，达到节省存储空间的目的。

文献[11]则提出了基于缓冲窗口的哈夫曼编码算法，该算法通过使用固定大小的窗口缓冲区来存放当前时间段出现的符号，随着文件中符号的依次读入，节点的权值随之进行更新。当缓冲窗口已满时，则删除窗口中最早存入的符号；同时更新与新进符号相关联的节点权重值，并调整哈夫曼树的形态。

基于上述的算法过程可以动态地生成一棵哈夫曼树，而由于符号的编码长度与树的深度成正比，因此，随着缓冲窗口中非重复符号的数量不断增加，依赖于这些符号的哈夫曼树的深度随之增加，这也就导致了符号的编码长度不断变长。最坏的情况下，符号的最大编码长度将达到（非重复符号的数量-1）位，如第1.1节中的示例描述。从表2和表3可知，符号E、F出现的频数只比缓冲窗口内其他的符号少一次，但是其哈夫曼编码的长度为5，体现了改编码方式的低效性，即使它们的频率相对较低。因此，在这种情况下，基于缓冲窗口的哈夫曼编码性能并不好。另一方面，基于缓冲窗口的哈夫曼算法的性能与窗口的大小有着直接的关系，因为在算法中使用的是固定大小的窗口，这导致该算法不能很好地适应不同类型的数据源。本文将对基于缓冲窗口的哈夫曼算法进行改进。

1.3 算法评价指标

（1）信息熵

信息熵[12]是指消息中包含信息量的平均值，可以表示为：

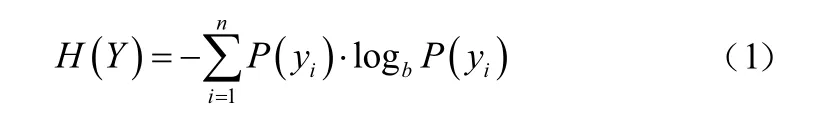
式中参数b是对数的底数。

（2）编码的平均长度

将符号出现的概率与该符号的编码长度值进行求积操作，就可以得到哈夫曼编码的平均长度，可表示为：

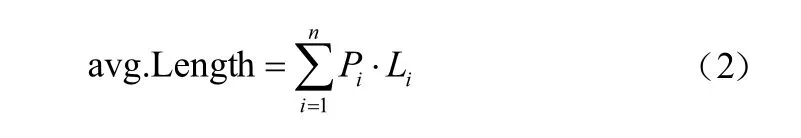
（3）信息冗余度

信息冗余度[13]在信息论中是指传输的信息的比特数与实际信息的比特数之差，即式（2）与式（1）的差，可表示为：

2 基于缓冲窗口的双哈夫曼编码算法（DHBW）介绍

为了解决上述提到的编码低效性和缓冲窗口无法自主地调整到最佳大小的问题，本文对基于缓冲窗口的哈夫曼算法进行了两个方面的改进。

2.1 限制缓冲窗口中符号种类的数量

DHBW算法中利用缓冲窗口来存储符号编码，该缓冲窗口中对不同符号的数量设置了阈值。需要说明的是，窗口中限制了不同符号的数量，而不是限制所有符号的数量。这是因为每个符号经过哈夫曼算法编码后的长度取决于不同符号的数量，与符号的总数量无关。缓冲窗口模型如图2所示。

图2 缓冲窗口模型

当缓冲窗口中不同符号的数量超过所设的阈值时，则重复删除最早的符号，直到不同符号的个数在阈值内。算法的步骤描述如下：

在传统的哈夫曼算法中通常采用数组等结构来进行存储，这种存储结构不易扩充，导致缓冲窗口的大小不能很好地适应不同类型的数据源。例如，缓冲窗口的大小size（N）=16，在进行编码时，如果编码位长度超过16位时就会发生数据溢出。因此，在本文提出的DHBW算法中利用线性链表[7]作为缓冲窗口的存储结构。这种改进能够使得算法中的缓冲窗口不受编码位数影响，只与内存大小有关。

2.2 基于缓冲窗口的双哈夫曼算法

在基于缓冲窗口的哈夫曼算法中，通常将不在窗口中编码的符号用转义码分开，然后用8位ASCII码进行编码，这样虽然能够缩短编码后的长度，但是当字符种类非常多时，仍存在编码后的码长过长的情况。为了进一步提升压缩效果，本文提出一种基于缓冲窗口的双哈夫曼算法，这里的“双”是指进行一次哈夫曼编码后，在编码的结果上再进行二次哈夫曼编码，算法过程如下：

Step1：将每个给定的符号作为一个叶子节点，并为其确定权值；

Step2：合并两个权值最低的节点；

Step3：节点的左分支标记为代码“0”，右分支标记为代码“1”；

Step4：计算Step2中合并后两个节点的概率之和；

Step5：在树中添加另一个节点，并执行Step2～Step4；

Step6：哈夫曼树构造完成后，分别计算树中叶子节点的熵值、平均长度值和冗余值；

Step7：在哈夫曼树生成后，根据左右分支的标记得出每个符号的编码，现在将这些代码字连接起来得到一个字符串；

Step8：将Step7中符号编码进行连接，形成一个只含有“0”和“1”的字符串，并且计算出该字符串中“0”和“1”的概率；

Step9：重复Step1～Step6。

这里以A、B、C、D、E、F这6个字符为例，字符的出现次数（视为权重值）见表3所列。

表3 符号频数表

利用上述的算法过程对表3中的字符进行处理，得到了如图3所示的哈夫曼树。其中，哈夫曼树中的每个节点左子树标记为“0”，右子树标记为“1”，则得到见表4所列的编码序列。

图3 由表3构造出的哈夫曼树

表4 符号编码序列表

根据第1.3节中的评价指标，分别计算该例子中的熵、平均长度和冗余度的值，结果见表5所列。

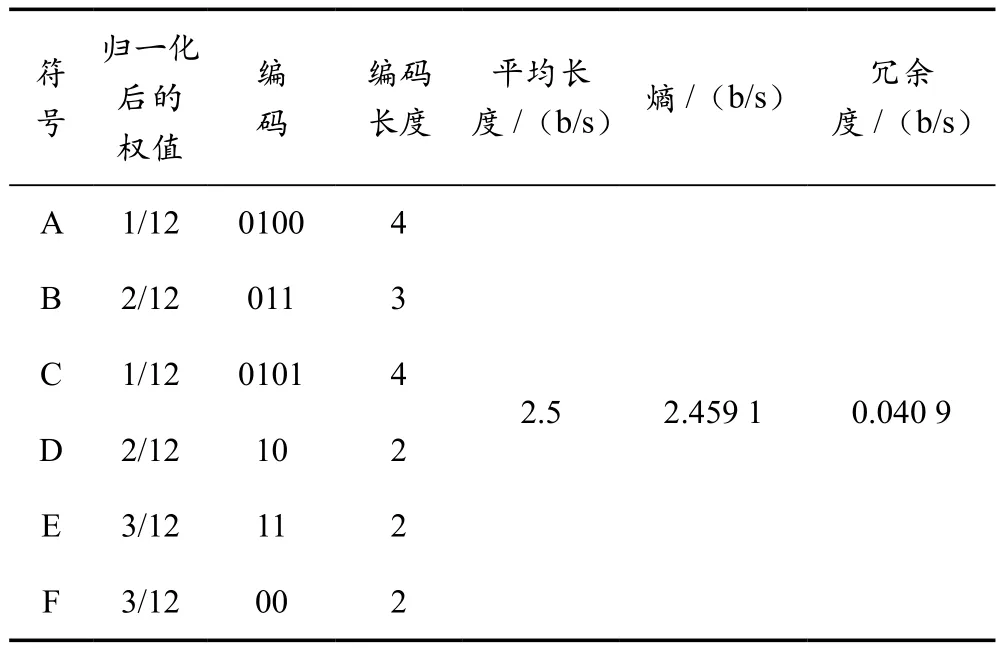
表5 哈夫曼编码的评价指标结果

在对原始符号进行一次哈夫曼编码后，将6位字符的编码进行连接，得到字符串“01000110101101100”，可以看到编码后的结果是只含有“0”和“1”的形式，且出现的概率分别为9/17和8/17。基于本文DHBW算法的思路，接下来将针对该结果进行二次哈夫曼编码。同样地，先根据符号出现的概率构造一棵只含有“0”和“1”的哈夫曼树，如图4所示。

图4 二次构造的哈夫曼树

根据左子树标记为“0”，右子树标记为“1”，得到见表6所列的编码序列；接着，分别计算二次编码后的熵、平均长度和冗余度的值，结果见表7所列。

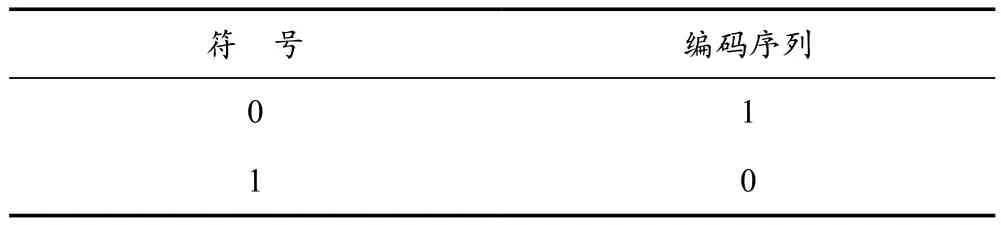
表6 符号编码表

以上结合具体的例子详细阐述了双哈夫曼编码的原理和过程，分别对比采用一次哈夫曼编码和二次哈夫曼编码的结果见表5和表7所列，从表中可以看出经过二次编码后的编码长度和信息冗余度均有下降，提升了有效信息的占比。

表7 哈夫曼编码的评价指标结果

3 实验过程与结果

为了验证本文提出的DHBW算法的有效性，分别与哈夫曼算法（Huffman）、基于缓冲窗口的哈夫曼算法（Windowed Huffman）进行压缩率和压缩速率的比较。选取不同类型、不同大小的文件，分别采用三种压缩算法进行压缩。

3.1 实验环境

实验是在操作系统为Windows 8.1，英特尔酷睿i7处理器，8 GB内存的环境下，利用Eclipse作为开发环境。实验数据采用了DOC、TXT和C++格式的文件，文件中的数据为英文文本，并包含部分数字。

3.2 实验结果与分析

（1）压缩率比较

选取大小为5 MB，15 MB，25 MB的文件，格式分别为DOC、TXT和C++的文件数据进行哈夫曼压缩、基于缓冲窗口的哈夫曼压缩和基于缓冲窗口的双哈夫曼压缩，得出的实验结果见表8所列[14]，其中：

压缩率=（1-压缩文件大小/输入文件大小）×100%

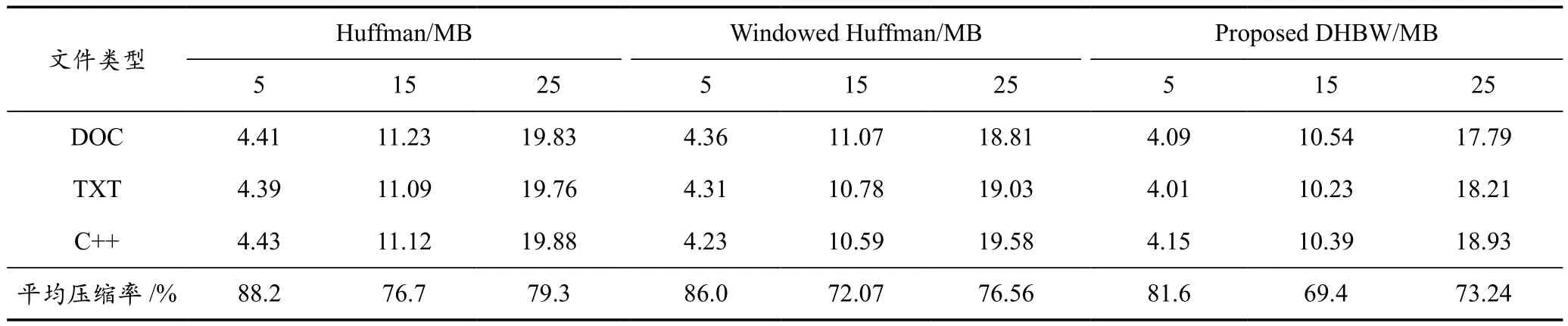
表8 不同算法的压缩率比较

由表8可以看出，本文提出的DHBW算法比传统的哈夫曼算法的压缩率分别降低6.6%，7.3%，6.06%；比基于缓冲窗口的哈夫曼算法的压缩率分别降低4.4%，2.67%，3.32%。由此可认为基于缓冲窗口的双哈夫曼压缩算法能够提升文件的压缩率。

（2）压缩速率比较

在使用三种压缩算法进行文件压缩时记录了压缩的时间性能，即平均压缩速率，结果见表9所列。从表中可以看出，本文提出的DHBW算法在压缩速率低于对比的两种算法，这是因为提出的DHBW算法需要进行3次数据扫描，因此会导致算法的整体压缩速率较低。

表9 三种算法的平均压缩速率 MB/s

4 结 语

本文在基于缓冲窗口的哈夫曼压缩算法基础上进行了两个方面的改进，首先，对缓冲窗口中不同符号的数量进行限制，以此来提升动态生成哈夫曼树的性能；其次，在一次哈夫曼编码的基础上再次进行只含有“0”和“1”哈夫曼编码，进一步降低字符的编码长度。实验结果证明，本文改进后的DHBW算法能够降低文件的压缩效果，但是需要耗费更多的时间。在未来的研究过程中，可以从提升压缩速率的角度出发，在保证压缩率的基础上也能保持较高的压缩速率。