多无人机协同监测Ad-Hoc网络组网方法研究
贺雄伟,王晋陶,胡欣宇,荆瑞俊,薛博文
(1.山西农业大学 软件学院,山西 晋中 030801;2.贵州电子科技职业学院,贵州 贵阳 550003;3.山西财经大学 管理科学与工程学院,山西 太原 030006)
0 引 言
我国作为农业大国,农业病虫害的监测及防治对粮食产量至关重要。近年来,随着无人机产业的快速发展,无人机农业遥感技术因其空间分辨率高、时效性强和成本低等特点,在农作物病虫害监测应用中发挥了重要作用[1]。但目前的应用大多以单无人机执行任务的方式为主,随着监测区域的变大、监测精度要求的提高以及监测结果实时处理的需求,单无人机执行任务能力不足的缺点越来越明显。多无人机协同执行任务必然成为一种趋势[2]。在多无人机协同执行任务时,通常会组成一个网络,即无人机Ad-Hoc网络[3-4]。网络构建的优劣对多无人机协同执行任务的性能产生很大影响,因而对组网方法进行研究成为多无人机协同控制的关键技术之一[5-6]。
针对多无人机组网方法,Parekh等人[7]提出一种最大节点度组网算法,该方法根据无人机的邻居数量进行网络分组。Vivek Yadav等人[8]针对各节点能量及处理能力的不同,提出了一种基于GNN(Grossberg Neural Network, GNN)的多无人机组网方法,该方法能够解决异构无人机的组网问题。文献[9]将节点的移动性、剩余电量、度,及与其他节点的平均距离作为评估标准,提出一种组合加权的簇头选择算法,该方法可以较好地解决多无人机组网问题。文献[10]针对移动Ad-Hoc易遭受攻击,网络安全性低等特点,在分组过程中加入了对节点安全性的计算评估,并作为选举簇首的参考之一。在簇首的选取中,优先选择安全性高的节点作为簇首,但上述方法存在以下不足:
(1)未将组网方法与具体任务相结合;
(2)对于组合加权组网方法中各长机的选取,主要考虑了无人机的剩余电量,而从负载均衡以及网络结构优化角度着手对长机的选取研究较少;
(3)对于通信距离约束下的多无人机组网方法未进行研究。
因此,本文以多无人机协同执行农业病虫害监测任务为研究背景,主要研究在通信距离约束下,如何通过控制各分组内部的无人机数量实现各无人机间的负载均衡以及网络结构的优化,进而达到提高多无人机协同农业病虫害监测效率的目的。
1 问题描述
假设多架携带有无线遥感设备以及通信设备的无人机对一块给定任务区域进行监测(各无人机通信距离有限),无人机在进入任务区域后,首先进行Ad-Hoc网络构建,然后基于构建的网络对任务区域进行监测,在监测过程中,各无人机依靠组建的网络进行信息交互,实现对任务区域的高效监测与覆盖。多无人机协同监测的典型场景如图1所示。
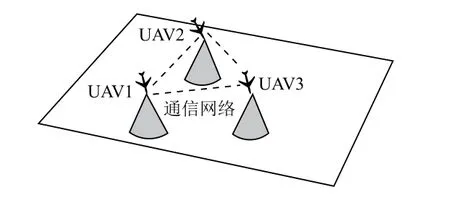
图1 多无人机协同区域监测示意图
2 多无人机协同区域监测问题建模
2.1 无人机运动学模型
假设各无人机的飞行速度和高度恒定。基于以上简化处理,给出飞机平台的运动学模型,以第i架无人机为例,其运动学方程如公式(1)所示[11]:
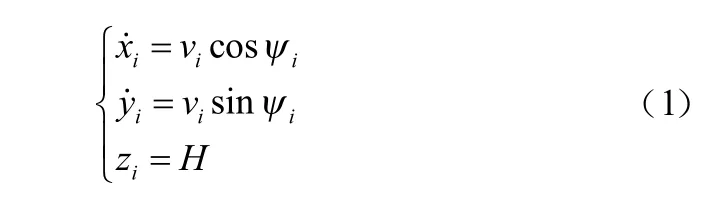
式中:(xi,yi,zi)表示当前时刻无人机i的位置;ψi为当前时刻无人机i的偏航角(0°≤ψi≤360°);vi为无人机i的速度(vmin≤vi≤vmax);H为给定的飞行高度。
2.2 无人机Ad-Hoc网络模型
无人机Ad-Hoc网络主要分为平面结构与分层结构[11-12]。本文中的无人机Ad-Hoc网络采用长机-僚机模型,网络结构如图2所示。
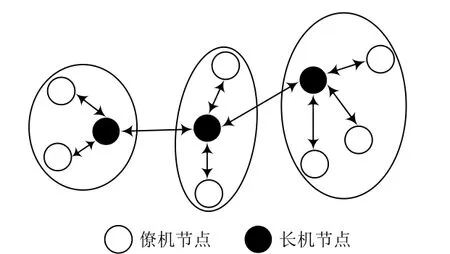
图2 无人机Ad-Hoc网络结构示意图
无人机在执行任务时首先进行Ad-Hoc网络构建,通过该过程形成分层的拓扑结构,各分组间通过长机节点进行信息交互。
2.3 通信距离约束
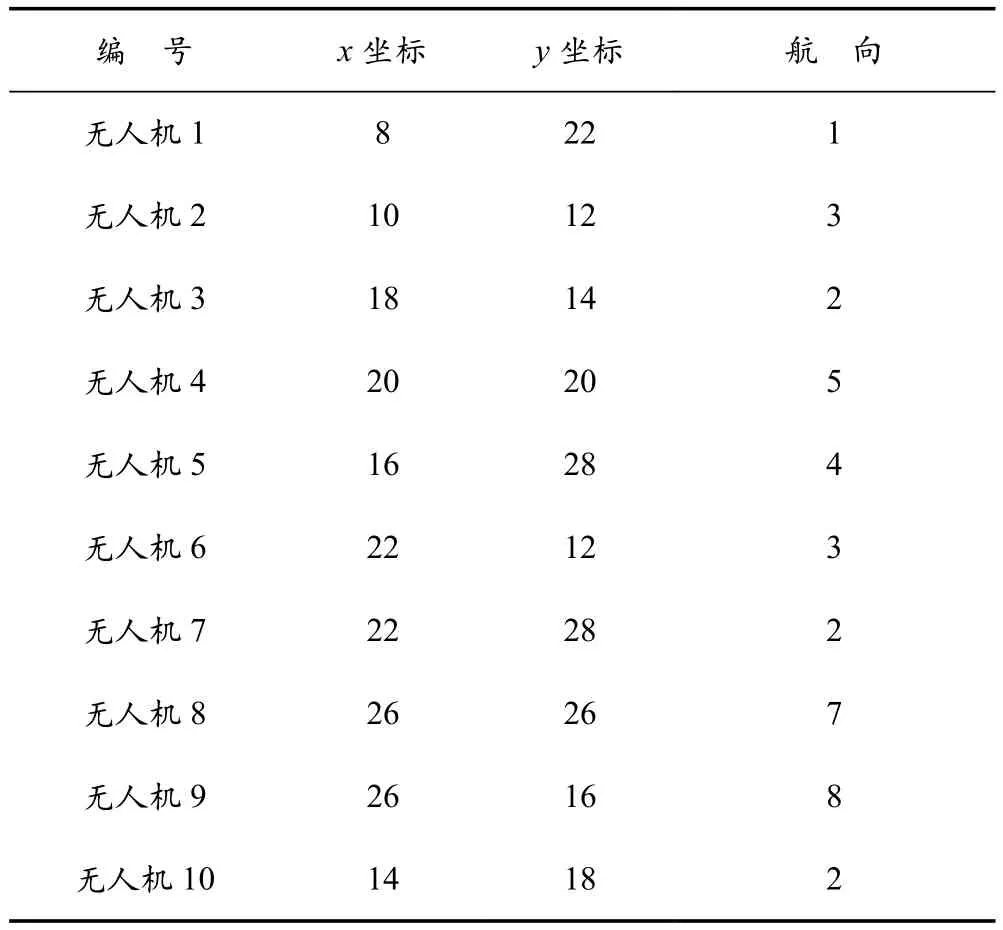
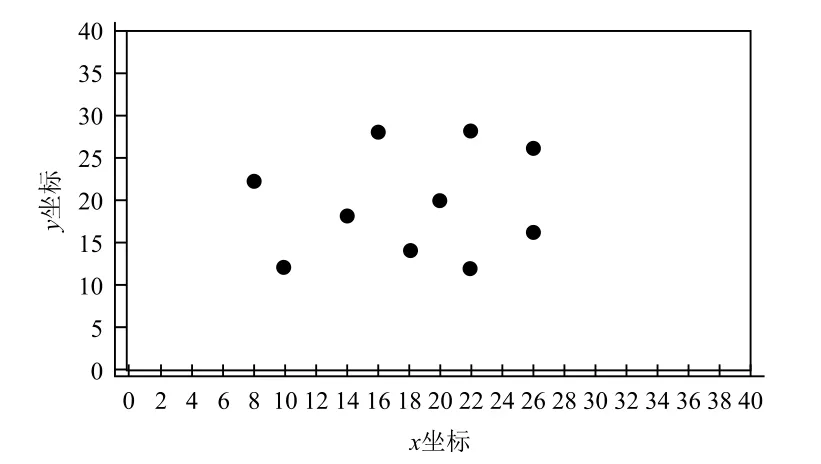
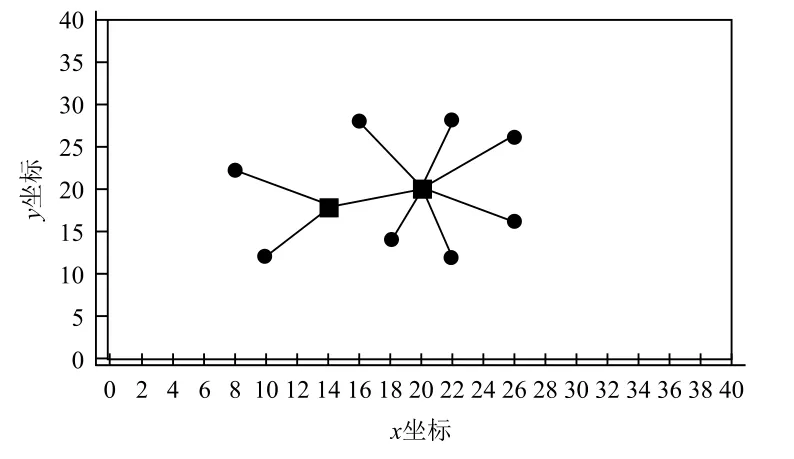
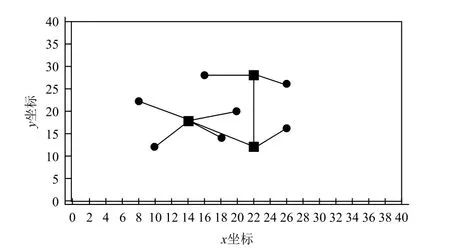
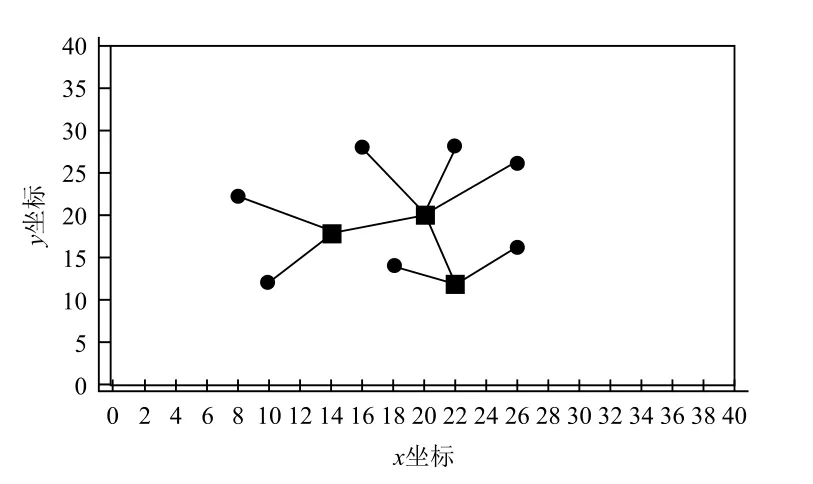
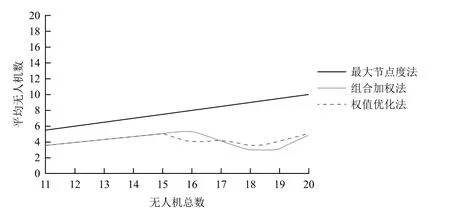
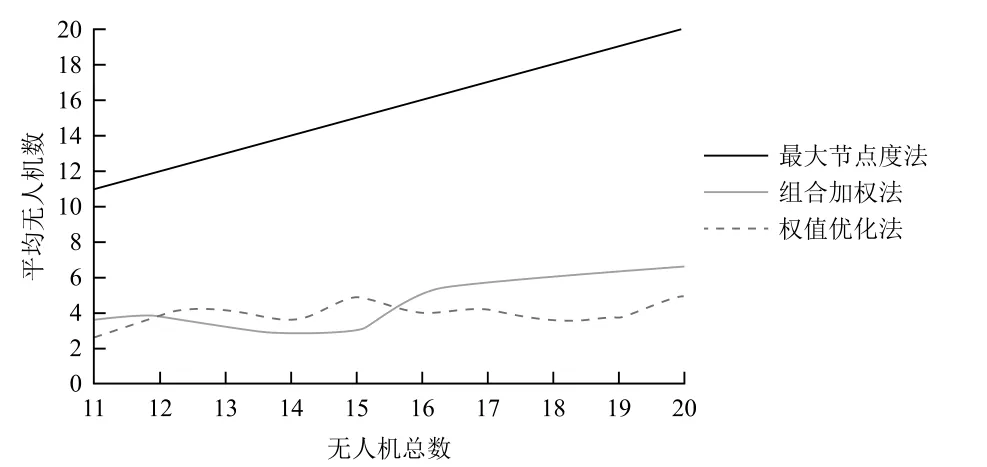
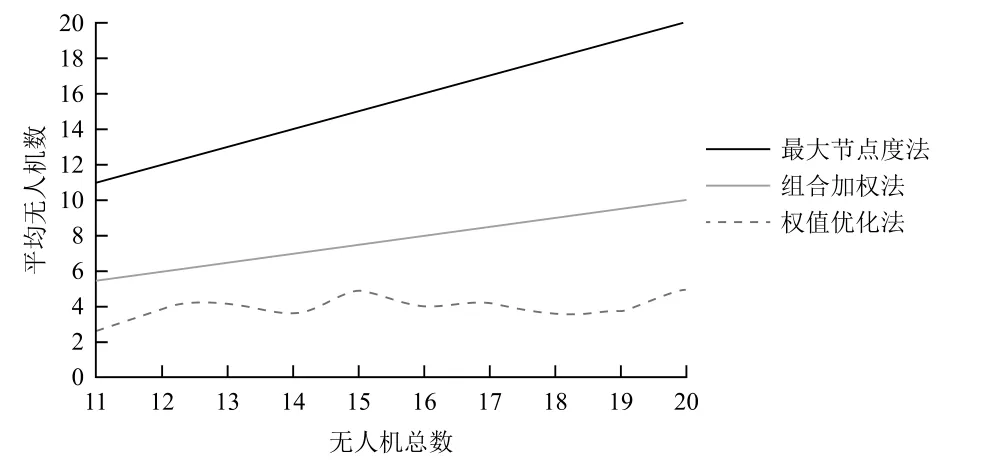
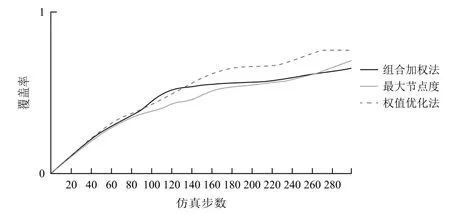
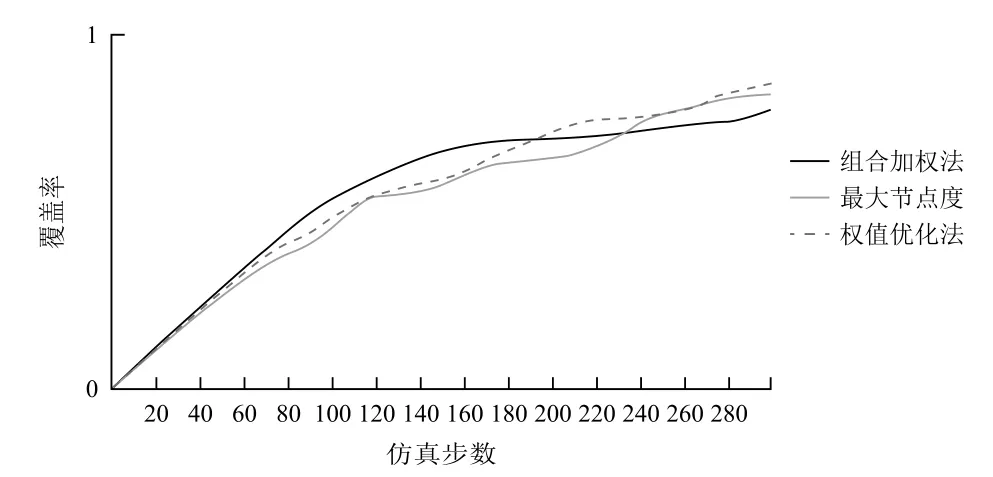
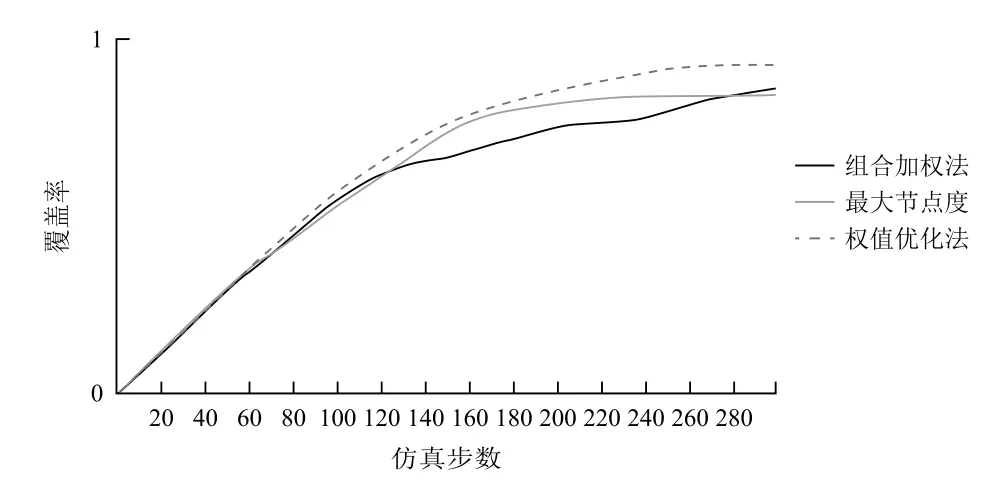
无人机执行任务时的通信方式为自由空间的无线通信。由于通信设备功率有限,因此无人机的通信距离有限。各无人机只有处于彼此通信范围内时才可以直接进行信息交互。由于本文中的无人机Ad-Hoc网络采用长机-僚机模型,因此给长机和僚机设置不同的通信距离。假设僚机通信距离为R1,长机通信距离为R2,且R1 Ad-Hoc网络构建完成后,无人机在保证网络连通的前提下对任务区域进行监测,为了实现对任务区域最大限度的覆盖,各无人机在进行下一航路点的选择时需要满足一定的准则。为此建立式(2)所示的飞行代价函数: 式中:p(x,y,t, ID)表示t时刻编号为ID的无人机地图坐标(x,y)处的信息素值,该值越小说明此单元格距离上次被监测的时间越长,因此网格中存在目标的可能性越大;q(x,y,t)表示该航路点的可行性,若无人机飞往该航路点可以保证网络连通,则该值为1,否则为无穷大;Disi代表下一可行点与无人机i的距离,该值越大无人机间碰撞的可能性越小;Dj代表各无人机与监测边界j的距离,该项主要使无人机远离监测区域边界;Δφ表示无人机从当前位置飞往下一可行点时所需转过的角度,该值越大表明飞往下一可行点所需的过载越大;S(x,y, ID)表示从当前位置飞往(x,y)处的总代价。 无人机在执行监测任务的过程中,通过代价函数计算公式实时计算,并选择代价值最小的航路点来尽可能降低环境的不确定性,从而实现对任务区域的高效监测。 无人机Ad-Hoc网络的拓扑结构对于多无人机协同监测效率有很大影响,而不同的组网方法所形成的拓扑结构各不相同。本部分从网络结构优化以及负载均衡的角度着手,提出一种有助于多无人机协同监测的权值优化有界节点度组网方法。该方法在组网时,考虑了无人机的邻居数量、与其他无人机的相对距离以及相对运动性等因素,在组网过程中设定了组内成员理想值Idel_NSlave,在保证满足无人机处理能力的前提下实现了负载均衡。具体的组网步骤如下: (1)为各无人机分配全局唯一的ID号; (2)选择ID号最小的无人机,根据权重计算公式计算该无人机的权重; (3)根据权重公式计算该无人机所有邻居节点的权重; (4)将权重最大的无人机定为长机,将该无人机分组标志位置1; (5)判断该长机所在分组中无人机数量是否达到理想值Idel_NSlave,若等于理想值则执行步骤(7),否则执行步骤(6); (6)判断步骤(5)所确定长机的所有邻居是否均已分组,若是,则执行步骤(7),否则在该长机的所有未分组邻居中选取权重最小的无人机加入长机所在分组,将该无人机分组标志位置1,长机所在分组中无人机总数加1,执行步骤(5); (7)判断是否所有无人机均已分组,若是,则结束分组,否则在未分组的无人机中选择距离上一次确定的长机最近的无人机,根据权重计算公式计算该无人机的权重,执行步骤(3)。 各无人机充当长机的权重见公式(3)所示: 式中:D为无人机的邻居数量;N为网络中的无人机总数;Dis为无人机与其所有邻居的相对距离;Max_Dis为相对距离的最大值;M为无人机的相对移动性;a1,a2,a3为各因素的权值系数,满足a1+a2+a3=1。 由于本文中假设各无人机的飞行高度不变,因此无人机间相对距离的计算可简化为二维平面内两点间距离的计算。计算公式如下: 式中:Disi表示无人机i与其他无人机的相对距离;K为第i架无人机的邻居数量;(xi,yi)为无人机i的位置坐标;(xj,yj)为邻居无人机j的位置坐标。 对于无人机相对移动性的评估以前后两个时刻无人机邻居的变化以及和其他无人机距离的变化为重点。分别介绍这两个指标的计算方法。 3.2.1 基于邻居变化的移动性度量 针对移动前后邻居的变化,本文通过建立历史档案来计算无人机的移动性。在历史档案中保存了每架无人机邻居的编号、位置、距离等信息,各无人机通过比较前一时刻和当前时刻历史档案中邻居节点的信息,得出移动前后邻居数量的变化,可进行无人机运动性的计算,计算公式为: 式中:n为移动前后未改变的邻居数量;n1为移动前无人机的邻居数;n2为移动后无人机邻居数。 3.2.2 基于邻居距离的移动性度量 针对移动前后无人机间距离的变化,本文使用无人机与其邻居之间距离方差的加权平均值来评估。在进行移动性计算时,通过比较前后两个时刻无人机与其邻居间距离的变化,得出各无人机距离的移动性,具体计算过程如下: (1)计算无人机N与其邻居M前后两个时刻的平均距离d,公式为: (2)计算节点N与其邻居M的距离方差c: (3)按照上述方法计算节点N与其所有邻居节点前后两个时刻的距离方差,记为{c1,c2, ...,cm},其中m为当前时刻节点N的邻居节点数,节点N的距离移动性指标为: 式中,ωi为无人机N与其邻居i通信链路的权值系数,若此链路越稳定,则权值ωi越小。 将基于邻居变化的移动性度量与基于邻居节点距离的移动性度量进行组合加权,可以得到最终关于节点移动性的度量方法。 式中,k1,k2为对于邻居变化和对于邻居相对距离变化的权值系数,本文选取k1=0.9,k2=0.1。 3.2.3 组内理想成员数的确定 在多无人机组网过程中,组内成员的多少对网络性能影响较大。若成员数量过少,则会导致分组数量过多,信息路由的平均长度与时延增大;若成员数量过多,则长机节点负载过重容易成为网络的瓶颈,因此必须选择合理的组内成员数量。为使网络实现最佳的负载均衡,本文引用参考文献[12]提出的关于最佳长机数的计算方法来计算理想组内成员数。 假设B1,B2分别表示组内和组间的链路带宽,Ntotal表示无人机总数,则可得最佳状态下的长机数Idel_NMaster为: 组内理想成员数Idel_NSlave为: 为验证本文所提权值优化有界节点度组网方法的有效性,选取最大节点度组网方法和组合加权组网方法作为对比,分别对上述3种组网方法在相同条件下所形成的网络结构、平均节点数随无人机总数变化以及在不同通信距离下对监测区域的覆盖率进行仿真分析。 仿真设定了一块40×40的正方形网格区域作为无人机的活动范围,在该范围内有10架携带有遥感设备以及无线通信设备的无人机在该区域内运动,各无人机的通信距离有限,无人机在运动过程中首先进行Ad-Hoc网络构建,然后基于飞行代价函数公式对任务区域进行协同监测。无人机初始信息见表1所列。仿真中,假设僚机的通信距离R1分别为10,15,20,长机通信距离R2=R1+10。 图3给出了无人机初始位置,图4~图6分别给出了僚机通信距离R1=10,长机通信距离R2=20时,最大节点度法、组合加权法、本文所提权值优化有界节点度法等3种组网方法所形成的网络结构。 这4幅图中,圆圈表示僚机,方格表示长机。由图3~图6可以看出,3种组网方法都选取了位置相对靠近中心的无人机作为长机,此类无人机具有相对移动性较小以及与其他无人机相对距离较近的优势,利于网络的稳定性,方便无人机间通信,表明了以相对移动性和与其他无人机的相对距离作为组网时所需主要考虑因素的合理性。最大节点度组网方法由于根据无人机的邻居数量进行长机的选取,导致形成的拓扑结构中分组间无人机数量相差较大。组合加权法和本文所提权值优化有界节点度组网方法由于在Ad-Hoc网络构建时考虑的因素较多,因此,最终形成的网络拓扑结构更优,无人机间的负载更均衡。 表1 无人机初始信息 图3 无人机初始位置 图4 最大节点度法 图5 组合加权法 图6 权值优化有界节点度法 图7~图9分别给出了在长机通信距离为20、25、30,僚机通信距离为(R1)10、15、20时,最大节点度法、组合加权法、权值优化有界节点度法等三种组网方法的平均无人机数随无人机总数的变化情况。 图7 R1=10时平均无人机数随无人机总数变化情况 图8 R1=15时平均无人机数随无人机总数变化情况 图9 R1=20时平均无人机数随无人机总数变化情况 由图中可以看出,在通信距离一定的情况下,最大节点度法和组合加权法的平均无人机数随无人机总数的增加呈增加趋势,权值优化有界节点度组网方法的平均无人机数随无人机总数的增加基本不变。这主要是因为随着无人机总数的增多以及通信距离的增大,每架无人机通信范围内的邻居数量增加,最大节点度和组合加权法在进行组网时,由于未对组内无人机数进行限制,因此,平均无人机数随无人机总数以及通信距离的增加而增加,但这不利于网络的负载均衡,长机由于处理的信息量较大,很容易造成网络拥塞。本文所提权值优化有界节点度组网方法在进行Ad-Hoc网络构建时,通过对分组内的无人机数设置理想Idel_NSlave参数,实现了各分组间无人机数量的均衡。 图10~图12分别给出了长机通信距离为20,25,30,僚机通信距离为(R1)10,15,20时,上述3种组网方法对同一块任务区域监测300步时的覆盖率曲线。 图10 R1=10时不同组网方法覆盖率曲线 图11 R1=15时不同组网方法覆盖率曲线 图12 R1=20时不同组网方法覆盖率曲线 由图可以看出,在通信距离相同的情况下,不同组网方法使用同一种监测方式的覆盖率各不相同,权值优化有界节点度法的覆盖率比组合加权法和最大节点度法的覆盖率高。造成这种现象的主要原因是:组合加权法和最大节点度法组网方法同一个分组内部无人机数量较多,由于各无人机需要在保证网络连通的条件下进行航路点的选择,因此,各无人机运动的自由性受到约束,导致无人机重复监测某些区域;权值优化有界节点度组网方法设置了分组内部成员的理想度数,可在保证节点间实时通信的基础上提高节点运动的自由性,能够引导各无人机向未知区域飞行,提高协同监测的覆盖率。随着通信距离的增加,3种方法的覆盖率均增加,表明了通信距离对于多无人机协同区域效率具有直接影响。 本文提出了一种权值优化有界节点度组网方法,在组网过程中考虑了通信距离以及负载均衡的约束,并将该组网方法与具体的农业病虫害监测任务相结合。仿真结果表明,本文所提组网方法有助于实现网络结构的优化、无人机间负载的均衡以及提高多无人机协同监测的效率。2.4 搜索代价函数
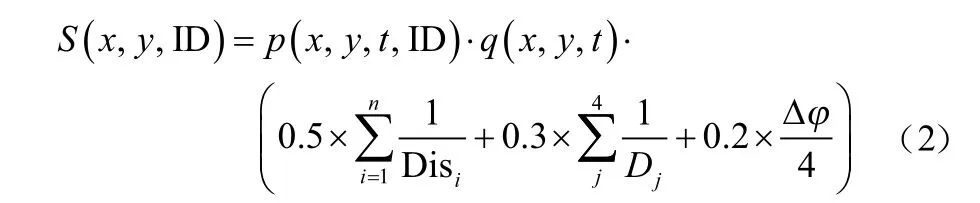
3 权值优化有界节点度组网方法
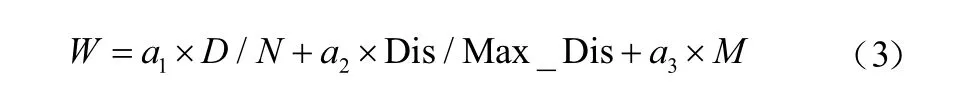
3.1 节点相对距离计算
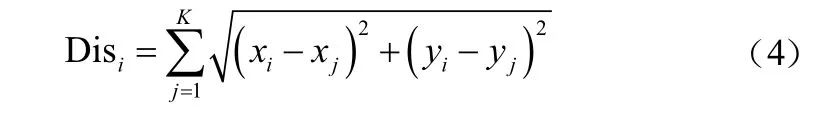
3.2 相对移动性计算
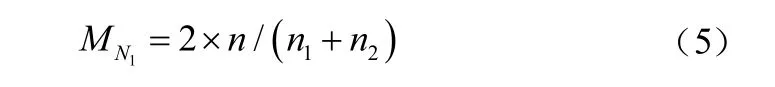
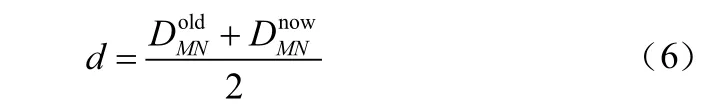
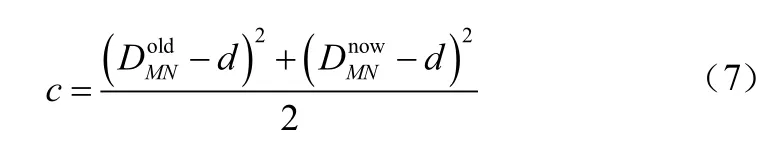

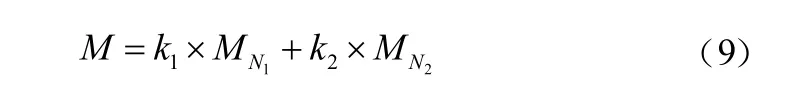
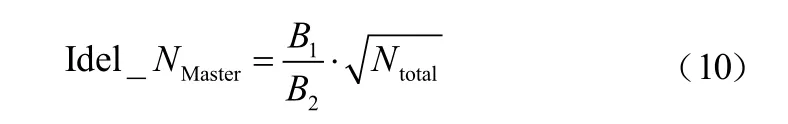
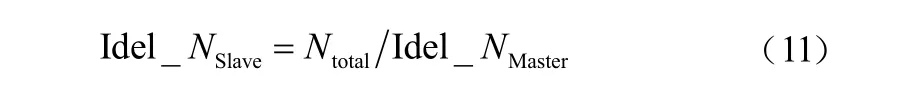
4 仿真验证
5 结 语

