不同绕组连接方式下的六相永磁同步电动机MT容错控制
李修东,郑晓钦
电机部分
不同绕组连接方式下的六相永磁同步电动机MT容错控制
李修东,郑晓钦
(青岛大学电气工程学院,山东 青岛 266071)
多自由度使多相电机具备了优异的容错能力。本文针对单中性点、双中性点及开端绕组结构的六相永磁同步电机,以缺相容错运行时输出转矩最大为目标,提出一种适用于不同绕组结构电机的容错电流计算通用表达式。通过对六相永磁同步电机缺一相故障状态下的自由度进行分析,计算了不同定子绕组结构下的容错电流,并给出相应的控制方法。对比三种不同绕组结构电机容错运行时的带载能力,开端绕组结构的六相永磁同步电机缺相容错运行时输出转矩最大。利用Matlab/Simulink建立了六相永磁同步电机模型及其控制系统,验证了计算结果的有效性。
六相永磁同步电动机;多自由度;绕组结构;容错控制
0 前言
近年来,多相电机在航空航天[1]、新能源汽车[2]、舰船推进[3-5]等领域都得到了十分广泛的应用。这源于多相电机使用低压功率器件即可实现较大的功率输出,尤其适用于供电电压受限的大功率场合。同时,多相电机具有较好的容错性能[6],相数的增加为多相电机提供了额外的自由度[7]。通过控制额外的自由度,多相电机可以实现故障后的稳定运行,从而提高系统的可靠性[8]。鉴于以上原因,针对于多相电机的容错控制一直是国内外学者研究的热点。
依据目标函数的不同,多相电机的容错策略多集中于带载能力最大化[9-13](Maximum Torque Capability, MT)与定子铜耗最小化[14-19](Minimum Loss, ML)。ML策略以故障前后定子合成磁势不变为约束条件[14],通过控制非故障相电流,使电机具备故障前的带载能力,但此时部分相容错电流幅值往往会超出额定值,如长时间运行,电机有进一步故障的风险[9]。MT策略则将容错电流值限制在额定值之内,以输出转矩最大为目标函数求解容错电流,最大转矩时各相电流大小相等且等于额定值[11],既保证了故障后电机的安全性,又使电机具备了最大的带载能力。因此在实际工程中更多的选用MT策略[11]。
对于MT策略的研究,文献[9]和[10]的研究对象为三套互移π/15电角度的五相绕组构成的半对称十五相感应电机,当某一相发生缺相故障时,仅故障相所在的五相绕组参与容错,其余两套五相绕组保持正常运行,这种方式虽未使剩余十四相全部参与容错,但对于相数较多的十五相电机而言,大大简化了寻找最优目标的过程。文献[11]使用MT策略实现了五相感应电机的容错控制,并在全转矩范围内进行了优化,既保证了电机具备最大的带载能力,又优化了电机的运行效率,增加了MT策略的实用性。文献[12]和[13]分别针对六相感应电机及永磁电机,研究了单中性点与双中性点半对称绕组结构的MT容错控制,但并未考虑开端绕组结构下电机的容错性能。
本文针对单中性点、双中性点及开端绕组结构的六相永磁同步电机(Permanent Magnet Synchronous Motor, PMSM),以缺相容错运行时输出转矩最大为目标,提出一种适用于不同绕组结构电机的容错电流计算通用表达式。首先建立了六相PMSM数学模型,采用d=0的控制方式实现了电机正常运行时的矢量控制;其次以缺a1相故障为例,分析单中性点、双中性点以及开端绕组三种结构下六相永磁电机自由度的损失,并进一步对比三种不同绕组结构下电机容错运行时的输出转矩;最后通过Matlab/Simulink进行仿真搭建,验证不同绕组结构下电机容错性能及容错控制策略的正确性。
1 六相PMSM矢量控制模型
六相PMSM通常采用矢量空间解耦矩阵进行坐标变换。依据文献[14]中关于解耦矩阵的定义,得到半对称六相绕组的矢量空间解耦矩阵为:

式(1)中一、二行对应为基波子空间,三、四行对应为五次谐波子空间,五、六行对应为零序子空间0+-0-。其中,直接参与机电能量转换,并决定圆形旋转磁势;、0+-0-不参与能量转换,仅影响电机的运行性能。
为便于驱动控制,需要将解耦变换后的交流量进一步旋转变换为直流量。考虑各谐波平面的旋转变换矩阵为:
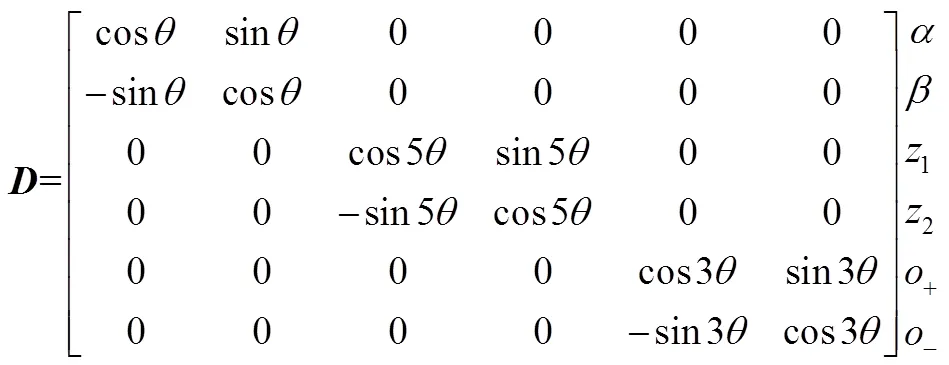
通过式(1)、(2)将六相PMSM从自然坐标系转换为同步旋转坐标系,可以实现电感矩阵的完全解耦,解耦后的定子电压方程为:


式中,永磁体磁链向量dq=[ψ0 0 0 0 0]T。
六相PMSM的电磁转矩可以表示为:

式(3)~(5)即为同步旋转坐标系下六相PMSM数学模型。
2 六相PMSM自由度分析
当多相电机发生缺相故障时,通过重构非故障相电流的幅值与相位可以实现故障电机稳定容错运行。以六相PMSM缺一相为例,当发生缺相故障时,故障相电流为零,非故障的五相电流幅值与相位均可提供一个自由度进行容错控制。MT策略以输出转矩最大为目标函数,转矩最大时各相电流幅值相等且等于额定值[11],因此仅剩余非故障相电流相位共五个自由度可参与容错控制。
在正交静止坐标系下,自由度的损失表现为各谐波平面电流不再相互独立,将会出现非独立电流。绕组连接方式的不同,六相PMSM原有的自由度不同,发生缺相故障后可参与容错的自由度也不同。本文以a1相缺相故障为例,分别对单中性点、双中性点以及开端绕组三种结构下的六相PMSM自由度依次进行讨论。
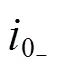
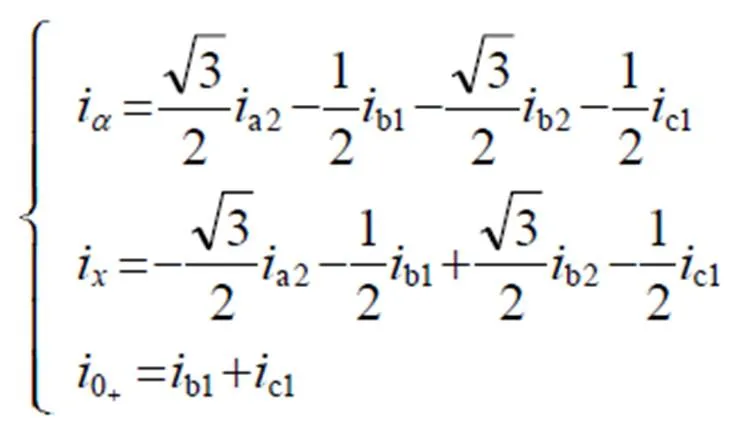
在单中性点、双中性点及开端绕组三种结构下均需要满足式(6)。
2.1 单中性点
正常运行时,单中性点绕组结构下的六相电流和为零。经解耦矩阵变换,在正交静止坐标系下体现为正负零序电流之和为零,即:

由式(7)可以看出,单中性点绕组连接方式使得两个零序电流不再独立,即单中性点绕组的六相PMSM只有五个独立电流。
当a1相断路后,剩余五相电流需满足:
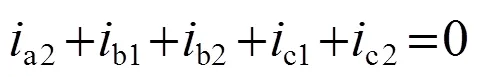
将式(8)代入式(6)进行整理,得到电流i、i与0+之间需满足:

从式(9)可以看出,a1相缺相使得电流0+失去了独立性,即缺相故障进一步导致自由度的缺失。
综合式(7)和(9),对于具有单中性点绕组结构的六相PMSM而言,发生一相缺相后,仅剩下四个自由度可以参与容错控制。
2.2 双中性点
对于双中性点绕组结构而言,两个中性点各自相互独立,需要保证每套三相绕组中的电流和均为零。变换至正交静止坐标系下,正负零序电流关系为:

从式(10)可以看出,对于双中性点绕组连接的六相PMSM,两个零序电流相等且都为零,即双中性点绕组的六相PMSM只有四个独立电流。
a1相断路后,剩余五相电流需满足:

将式(11)代入式(6),得到正交静止坐标系下的各谐波电流关系为:

由式(12)可知,当发生缺相故障时,a1相所在的三相绕组中剩余两相电流都将受到影响,变换到正交静止坐标系下表现为电流i失去了独立性。因此,对于具有双中性点的六相绕组而言,缺一相容错时仅有三个自由度可以独立控制。
2.3 开端绕组
对于六相开端绕组,每相电流均可实现独立控制,变换到正交静止坐标系下相应的基波及各次谐波电流均相互独立。
当a1相故障时,依据式(6),在正交静止坐标系下受故障影响的电流量i、i与0+具有线性关系,即:


对于开端绕组结构的六相电机,缺一相容错运行时,可以独立控制五个电流分量,能最大限度发挥六相绕组的容错能力。
3 六相PMSM容错电流计算
在容错运行中,为避免过大的电流导致功率器件或电机过热而引发进一步的故障,需要对电机的容错电流进行限制,有:
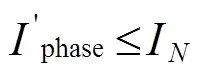
式中,I为额定电流幅值;Iphase为各相容错电流幅值。
为更准确的描述容错控制时电机的输出转矩,引入文献[10]中的转矩降额系数以及电流降额系数。其中转矩降额系数(K)用来表示容错控制前后电磁转矩的降额程度,即:
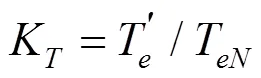
式中,T表示容错降额运行时的输出转矩;T表示额定电磁转矩。
在d=0的控制方式下,电流降额系数(K)可表示为:

依据六相PMSM电磁转矩表达式(5),此时的K与K满足以下关系:
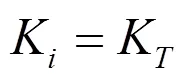
为使容错运行时电机输出转矩最大,就要使转矩降额系数(K)最大。由式(17)可知,对于采用d=0控制方式的六相PMSM,保持电流降额系数(K)最大即可保证输出转矩最大。
为保证容错电流形成圆形旋转磁势,消除故障所引起的基波反转磁势,因此在两相静止坐标系下,平面的基波电流需满足以下形式:

缺相容错运行时,基波电流i、i决定圆形旋转磁势,-0+-0-平面的谐波电流则提供额外的自由度进行容错控制:

式中,1、2…8为容错电流的待定系数。若电流为独立变量,则值可以根据转矩降额系数(K)最大的要求任意取值;若电流为非独立变量,则系数需依据约束关系,由独立变量决定。
式(19)即为容错电流计算的通用表达式,具体应用需要结合绕组结构进行具体讨论。
利用解耦矩阵的逆变换矩阵,将式(18)和(19)变换至自然坐标系下可得:
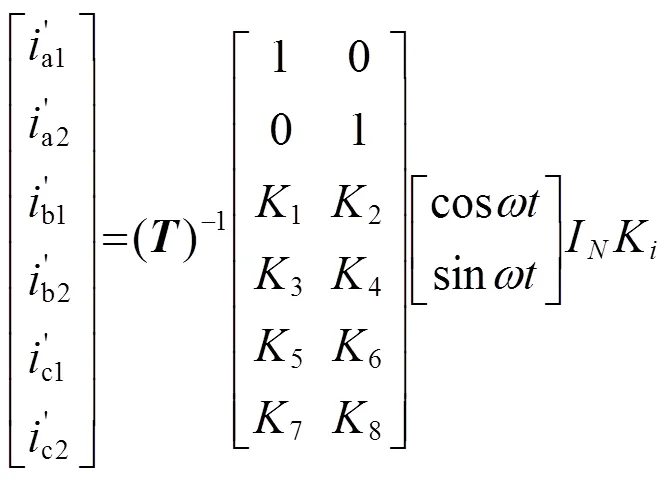
依据式(20),利用Matlab中的优化工具即可求解K的最大值。表1、2、3依次给出了单中性点、双中性点及开端绕组三种结构下所对应的待定系数及转矩降额系数K。

表1 单中性点结构下的六相绕组容错参数
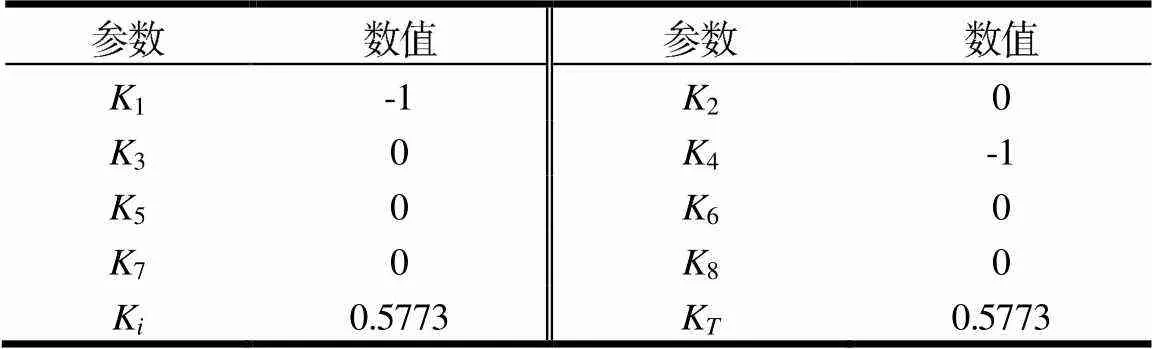
表2 双中性点结构下的六相绕组容错参数
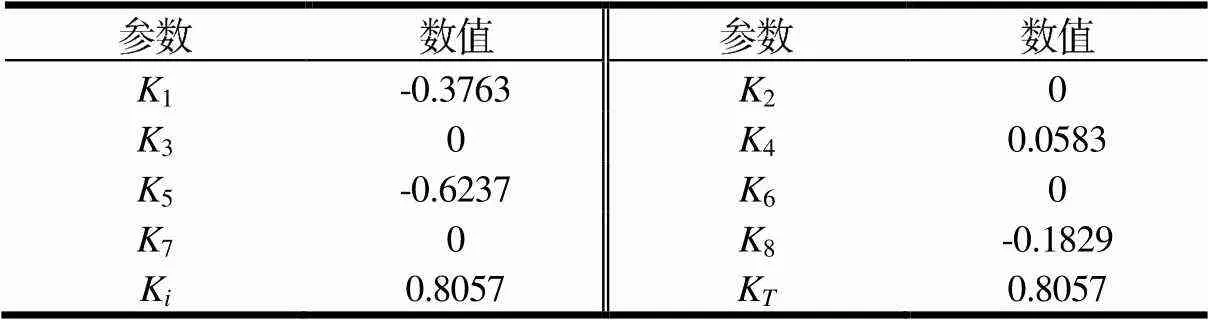
表3 开端绕组结构下的六相绕组容错参数
将表1、2、3中的容错参数依次代入式(20)即可求解三种中性点结构下的容错电流。
单中性点绕组结构的各相容错电流为:

双中性点绕组结构的各相容错电流为:

开端绕组结构的容错电流为:
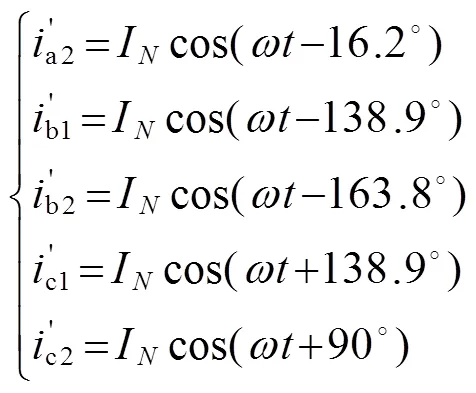
不同绕组连接方式下的容错电流向量图如图1所示。其中,图1(a)、(b)、(c)依次为单中性点,双中性点及开端绕组结构下的容错电流。

图1 不同绕组连接方式下的容错电流向量图
值得说明的是,以上均是以a1相故障为例,对不同绕组结构的六相PMSM容错电流进行计算。当其他相发生缺相故障时,需根据受影响的电流分量重新确定式(6),按照中性点的连接方式计算相应的值。
4 六相PMSM容错控制的实现
图2给出了六相PMSM容错控制框图。为使容错控制在正常运行控制的基础上尽可能少的改动,图2(a)所示的基波平面q轴电流仅乘以降额系数K即可;谐波平面电流需增加一个电流计算模块,如图2(b)所示,依据式(19)计算各谐波平面下的电流给定值。由于及0+-0-电流分量在容错时不为圆形轨迹,这里采用双PI控制器对正负序分量进行分别控制,如图2(c)所示,正常运行时则无需控制负序分量。其中,六相PMSM容错控制的总框图如图3所示。
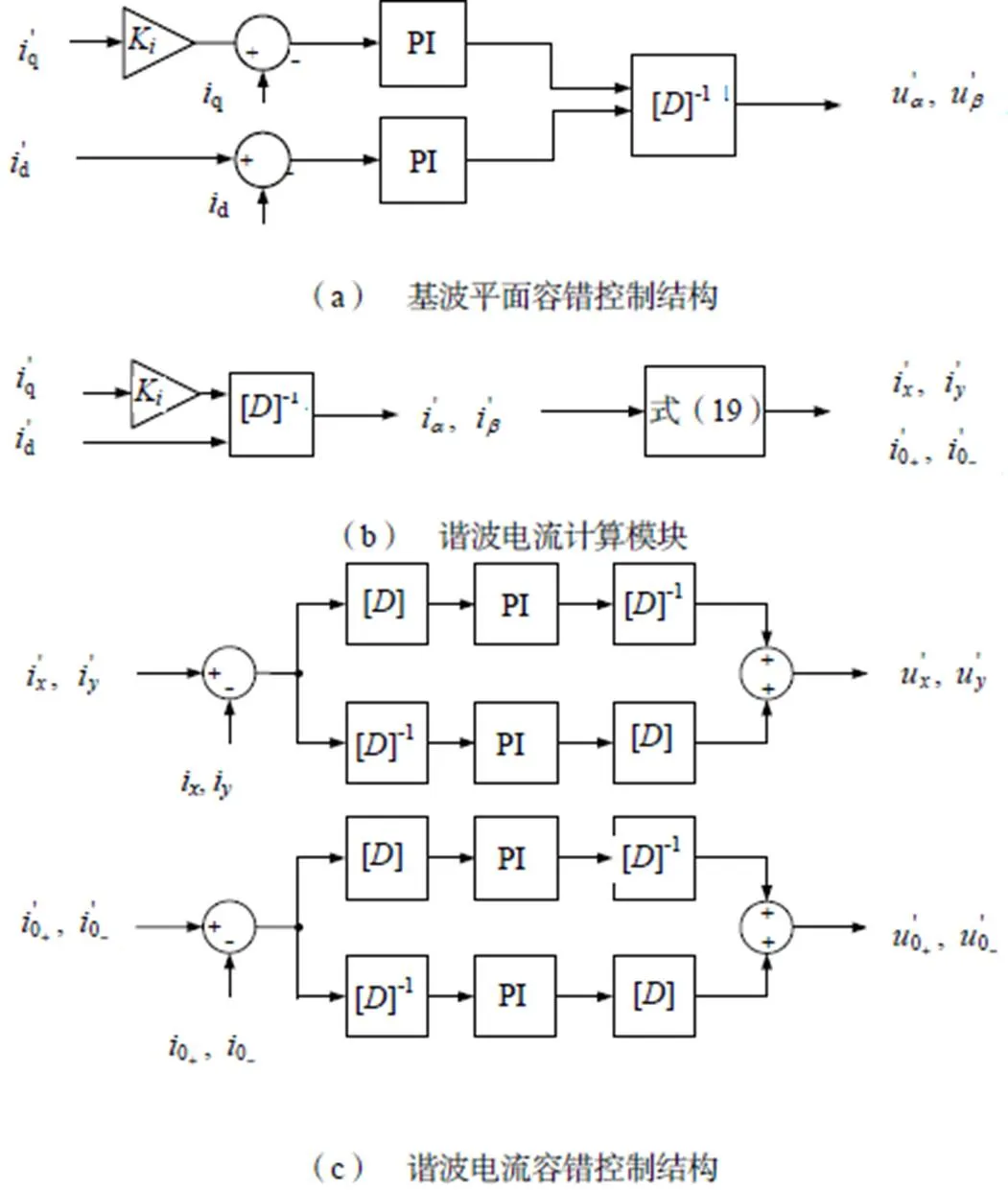
图2 六相PMSM容错控制框图

图3 六相PMSM容错控制总框图
5 仿真验证
基于Matlab/Simulink建立三种绕组连接方式下统一的六相PMSM容错控制系统,如图3所示。由于MT策略在容错前后不改变电机的数学模型,因此六相PMSM正常运行、缺相运行及容错运行时具有相同的电机模型。三种绕组结构下的六相PMSM正常运行时,双PI控制器无需控制负序分量,式(19)中各谐波电流指令均为零;容错运行时,双PI控制器需控制负序分量,并依据表1、2、3给予不同的电流指令。仿真所使用的六相PMSM的具体参数见表4。

表4 六相PMSM参数
5.1 正常运行
图4为正常运行时六相PMSM带额定负载并稳定在额定转速1000r/min时的仿真波形。从图4可以看出,六相电流为标准正弦量且稳定在额定值,平面下的电流轨迹为标准圆形,这保证了相电流可以合成圆形旋转磁势,同时电磁转矩与转速同样稳定在各自的额定值。

5.2 缺a1相故障运行
六相PMSM带额定负载并稳定于额定转速时,使a1相电流为零进而模拟断相故障。从图5可以看出,故障运行时,各相电流的幅值与相位均发生了较大的变化,部分电流超过了额定值,电机有进一步故障的风险。同时平面下的电流轨迹畸变为椭圆形,产生了基波反转磁动势,这使电磁转矩与电机转速出现了2倍频脉动。
5.3 缺a1相容错运行
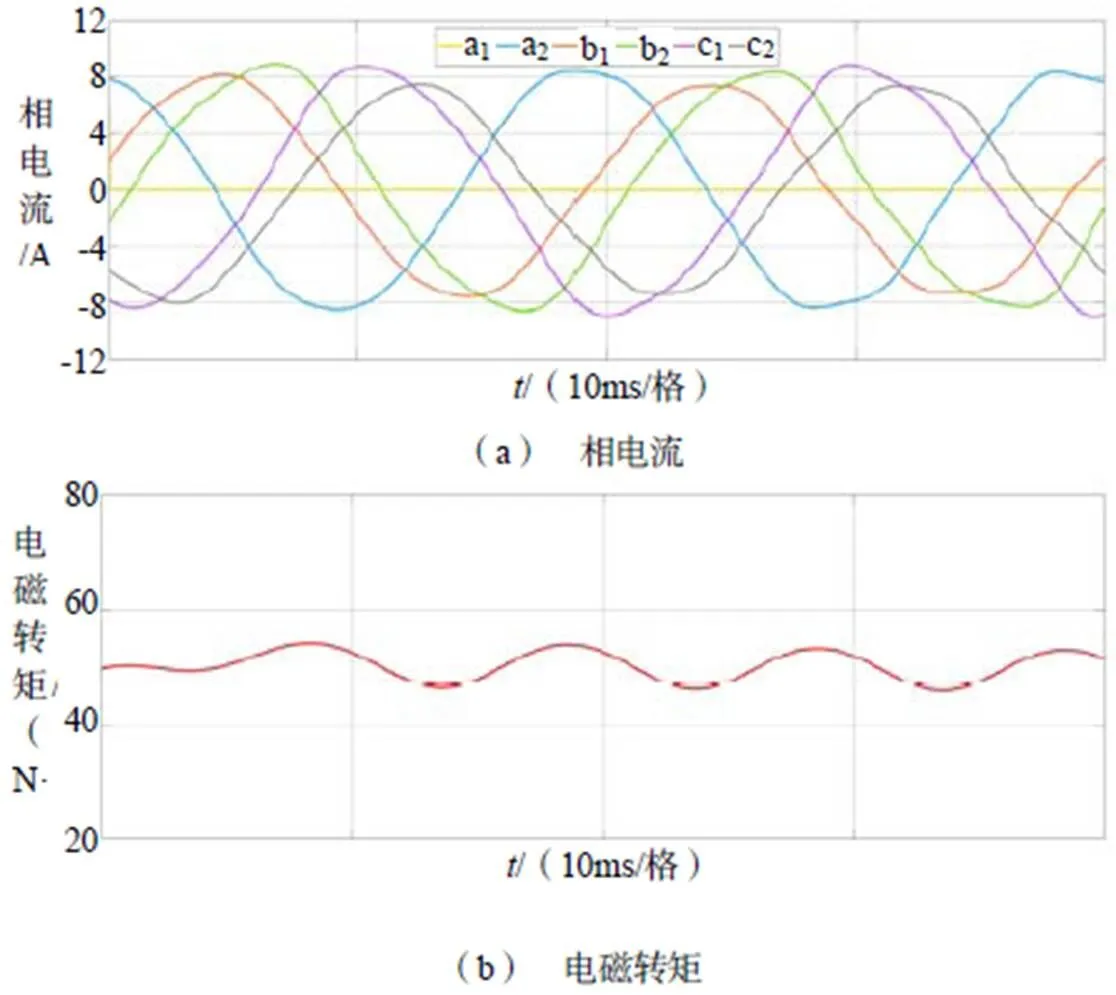
图6所示为单中性点绕组结构的六相PMSM容错运行仿真结果。从图6可以看出,剩余的五相电流幅值均相等且为额定值,平面下的电流轨迹恢复为标准圆形,消除了缺相引起的基波反转磁势,也进一步抑制了电磁转矩与电机转速脉动,其中电磁转矩降额到额定值的0.6944倍,与表1分析结果一致。
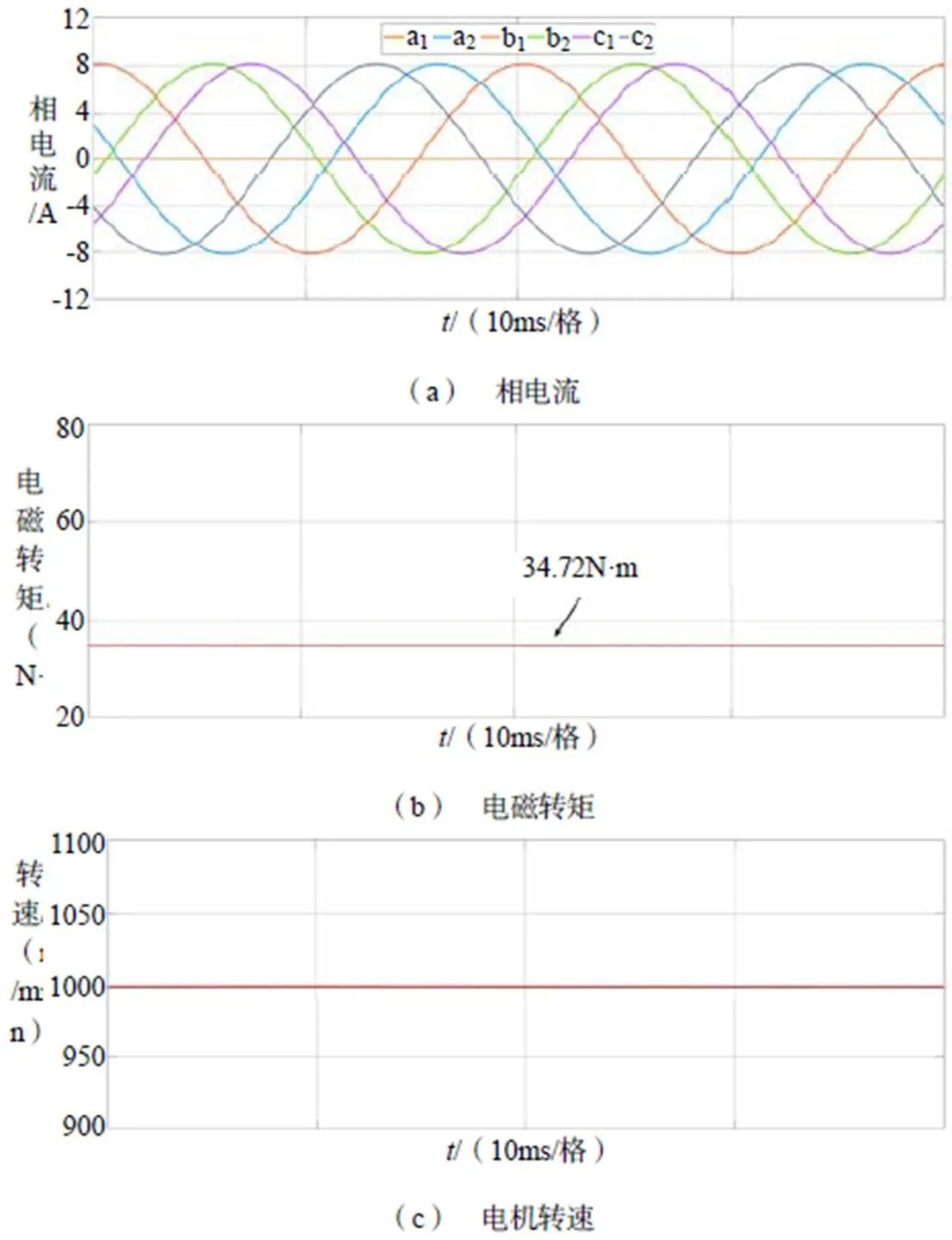
具有双中性点绕组结构的六相PMSM容错运行仿真结果如图7所示。平面的电流轨迹同样恢复为标准圆形,由于容错时自由度较少,电磁转矩降额为额定值的0.5773倍,降额比较严重。

图8为具有开端绕组结构的六相PMSM容错运行仿真结果。平面电流轨迹同样恢复为标准圆形,剩余五相容错电流幅值相等且为额定值,电磁转矩降额为额定值的0.8057倍。相比于以上两种绕组连接方式,开端绕组结构的六相PMSM在容错运行时具有最大的电磁转矩。
6 结论
本文针对于单中性点、双中性点及开端绕组结构的六相永磁同步电动机,提出一种适用于不同绕组结构电机容错电流计算的通用表达式。在正交静止坐标系下,利用矢量空间解耦矩阵对三种结构下的电机自由度进行了分析,计算出相应的容错电流及转矩降额系数,并给出统一的控制结构。通过Matlab/Simulink,建立六相永磁同步电机的容错仿真模型,验证了计算结果的正确性。通过对比三种绕组结构下六相永磁同步电机容错运行的输出转矩,可以看出,开端绕组结构的六相永磁电机容错性能最好,输出转矩最大,单中性点及双中性点结构则会额外损失自由度,从而降低带载能力。
[1] 陶涛, 等. 多相电机容错控制及其关键技术综述[J]. 中国电机工程学报, 2019, 39(2): 316-326.
[2] 周荔丹, 等. 多相永磁同步电机控制及风电应用综述[J]. 电气传动自动化, 2016, 38(1): 7-15.
[3] 刘自程, 等. 船舶电力推进中十五相感应电机同轴运行及容错控制策略[J]. 电工技术学报, 2014, 29(3): 65-74.
[4] 匡志, 等. 十五相永磁同步电机的驱动控制与容错运行[J]. 电工技术学报, 2019, 34(13): 2734-2743.
[5] 魏永清, 等. 十二相永磁电机驱动系统的容错控制策略[J]. 电工技术学报, 2019, 34(21): 4467-4473.
[6] 刘自程, 等. 多相电机控制驱动技术研究综述[J]. 电工技术学报, 2017, 32(24): 17-29.
[7] Duran M J, Barrero F. Recent advances in the design, modeling, and control of multiphase machines: Part II[J]. IEEE Transactions on Industrial Electronics, 2016, 63(1): 459-468.
[8] 於锋, 程明, 夏子朋, 等. 3种谐波电流注入模式下的磁通切换永磁电机缺相容错控制[J]. 中国电机工程学报, 2016, 36(3): 836-844.
[9] 郑晓钦, 等. 十五相感应电机不对称缺相容错运行控制[J]. 中国电机工程学报, 2016, 38(4): 1212-1221.
[10] 刘海涛, 等. 适用于多种缺相故障的十五相感应电机统一容错控制[J]. 中国电机工程学报, 2019, 39(2): 327-336.
[11] 刘海涛, 等. 五相感应电机缺相容错运行的全转矩范围效率优化控制策略[J]. 中国电机工程学报, 2020, 40(5): 1642-1652.
[12] Che H S, et al. Postfault Operation of an Asymmetrical Six-Phase Induction Machine With Single and Two Isolated Neutral Points[J]. IEEE Transactions on Power Electronics, 2014, 29(10): 5406-5416.
[13] 周长攀, 等. 基于正常解耦变换的双三相永磁同步电机缺相容错控制策略[J]. 电工技术学报, 2017, 32(3): 86-96.
[14] 王海兵. 双三相永磁同步电机高性能调速系统及容错运行研究[D]. 浙江大学, 2017.
[15] 於锋. 九相磁通切换永磁电机系统及容错控制研究[D]. 东南大学, 2016.
[16] 赵美玲, 全力, 张超, 等. 基于铜耗最小的五相永磁同步电机单相断路故障解耦容错控制[J]. 电机与控制应用, 2017, 44(12): 126-133.
[17] 周华伟, 等. 五相圆筒永磁电机统一容错矢量控制[J]. 中国电机工程学报, 2019, 39(5): 1479-1488.
[18] Jiawei Sun, et al. An Online Global Fault-tolerant Control Strategy for Symmetrical Multiphase Machines with Minimum Losses in Full Torque Production Range[J]. IEEE Transactions on Power Electronics , 2020, 35(3): 2819-2830.
[19] 彭忠, 等. 基于虚拟绕组和全阶观测器的五相感应电机无速度传感器容错控制策略[J]. 电工技术学报, 2018, 33(21): 4949-4961.
The MT Fault Tolerant Control of Six-phase Permanent Magnet Synchronous Motor with Different Winding Connection Modes
LI Xiudong, ZHENG Xiaoqin
(College of Electrical Engineering, Qingdao University, Qingdao 266071, China)
The degree of freedom makes the multi-phase motor have excellent fault tolerance. In this paper, aiming at the single neutral point, double neutral point and starting winding structure of the six-phase permanent magnet synchronous motor, a general expression for the calculation of fault-tolerant current applicable to the motors with different winding structure is proposed in order to maximize the output torque when running without phase tolerance. Based on the analysis of the degree of freedom of the six-phase permanent magnet synchronous motor in the state of a1phase fault, the fault-tolerant currents of different stator windings are calculated, and the corresponding control methods are given. Compared with the load capacity of three kinds of motors with different winding structure, the output torque of phase fault tolerant of the starting winding structure is the largest. The six-phase permanent magnet synchronous motor model and its control system were established by using Matlab/Simulink, which verified the validity of the calculated results.
six-phase PMSM; degree of freedom; winding structure; fault-tolerant control
TM341
A
1000-3983(2021)01-0001-08
国家自然科学基金资助项目(51907093);山东省自然科学基金资助项目(ZR2019BEE009)
2020-07-21
李修东(1997-),青岛大学电气工程专业硕士研究生,从事多相永磁同步电机容错控制方面的研究工作。


