基于频率加权能量算子与1.5维谱结合的发电机特征振动信号增强
何玉灵,孙 凯,王 涛,白 洁
基于频率加权能量算子与1.5维谱结合的发电机特征振动信号增强
何玉灵,孙 凯,王 涛,白 洁
(华北电力大学机械工程系,河北 保定 071003)
针对多极发电机故障振动信号信噪比低,故障识别难度高的不足,本文提出了频率加权能量算子(FWEO)与1.5维谱结合的方法来对发电机振动信号进行特征增强和滤噪。该方法应用频率加权能量算子来提取瞬态冲击特征和滤噪,应用1.5维谱来进行信号的二次特征增强和抑噪。对3对极发电机定子匝间短路故障前后定子振动数据的处理效果表明,本文所提方法能有效对发电机特征振动信号进行增强并实现有效滤噪,实现故障的快速识别;其处理效果不仅优于单一的频率加权能量算子和单一的1.5维谱,而且与当前流行的最大相关峭度解卷积算法相比具有一定优越性。
多对极发电机;定子匝间短路;振动信号;频率加权能量算子(FWEO);1.5维谱
0 前言
发电机是电力生产的核心设备,保障发电机组的安全稳定运行对于社会经济发展和关系国计民生行业的电力供应具有重要意义。
目前,普遍采用定、转子电压与电流变化特性、电磁转矩波动特性、定转子振动特性、绕组电感矩阵变化等参量来对各类故障进行监测与识别。这其中,振动信号由于包含丰富的故障信息,且传感器安装、信号测取方便,被方泛应用于工程实践中[1]。
近年来,国内外学者对信号处理方法进行了许多研究,滤噪处理技术和模式识别技术都在不断发展[2-8],旋转机械故障信号的提取技术取得了不断突破[9-11],能量算子在信号处理领域的应用也逐渐广泛[12-15]。在现有成果中,研究人员主要针对的是滚动轴承的故障信号,对发电机振动信号的滤噪和增强检测报道相对较少。相对而言,滚动轴承的振动信号的冲击特性要较发电机振动信号更为明显,这与轴承及电机的结构差异和运行方式有关。发电机的定转子质量及结构尺寸较大,除风力发电机外,汽轮发电机和水轮发电机运转相对平稳,系统等效阻尼也较滚动轴承要大得多,基于磁场作用的非接触电磁激励导致的机构振动响应在量级上也远不如滚动轴承因机械式接触产生的冲击激励直接产生的振动。
目前,一对极发电机的振动信号作快速傅里叶变换(FFT),或经常规简单的滤波去噪处理后经FFT所得到的频谱,其特征频率成分相对明显,基本可实现对故障类别的诊断与识别。但对于多极发电机,由于机械转频较低,作傅里叶变换后其频谱包含的频率成分也较一对极发电机要丰富得多,加上随机噪声和各类扰动信号的加成,所得到的特征频率成分往往被噪声信号所覆盖。例如,文献[16]中报道的定子匝间短路下的定转子振动特征频率成分(2、4、6)[17]对应的幅值就远低于其他非特征频率成分幅值,即特征成分无法突显,特征信号被覆盖,给故障的识别和诊断带来了很大的困难。如何对多极发电机的特征振动信号进行有效增强,同时抑制环境噪声等其他非特征信号,是当前领域内的重要课题。
本文采用频率加权能量算子(Frequency Weighted Energy Operator, FWEO)与1.5维谱结合的方法对多极发电机的定子振动信号进行处理,增强发电机的特征振动信号,并和单一的频率加权能量算子、单一的1.5维包络谱以及文献[18]中的最大相关峭度解卷积(MCKD)算法的处理结果进行对比。
1 频率加权能量算子
1.1 Teager能量算子
Teager能量算子(Teager Energy Operator,TEO)最初是Teager在研究非线性语音建模时,对窄带信号能量计算和追踪时引入的算法[19]。
对于任意的连续信号(),Teager能量算子的表达式为:
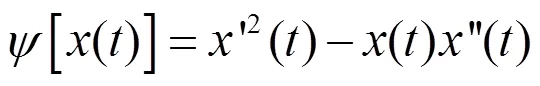
式中,'()和'()分别代表()的一阶导数和二阶导数;[()]为动能和势能的总和,即Teager能量算子。
相应地,离散能量算子的表达式为:

对于一组连续信号:
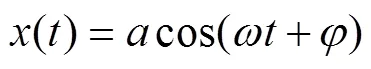
式中,代表幅值;代表瞬时频率。
求导得:


将式(3)、式(4)和式(5)代入式(1)得到:


从式(6)中可以发现,Teager能量算子中信号的总能量由幅值和频率共同决定。
联立式(6)和式(7)可得信号的瞬时频率和瞬时幅值:
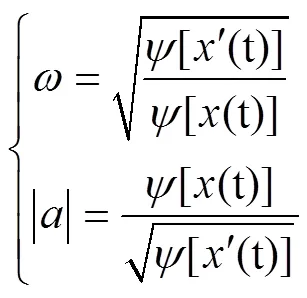
Teager能量算子通过对原始信号、一阶导数和二阶导数进行非线性组合,可以估计信号中的瞬时能量波动,进而实现瞬态冲击特征的提取。
1.2 频率加权能量算子
因为Teager能量算子解调容易受到干扰信号的影响并存在没有意义的负能量,所以Toole等人在满足TEO的相类似性质的基础上,选择信号的导数函数作为加权滤波器,提出了频率加权能量算子[20]。
连续信号频率加权能量算子的表达式为:

对于连续信号式(3)可继续得:
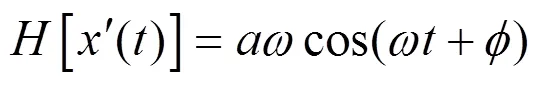
将式(4)和式(10)代入式(9)得:
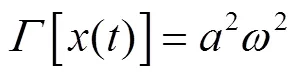
由此可见,频率加权能量算子具有同Teager能量算子相似的性质。
对比式(1)与式(9),Teager能量算子与频率加权能量算子的第一部分是相同的,区别主要是在第二部分。这些差别在频域上会表现得更加明显,分别计算第二部分对应的傅里叶谱如下:

式中,()表示()的傅里叶谱;*表示卷积操作。
频率加权能量算子是一种在传统能量算子的基础上对其频率进行加权的新算法,不仅能实现对信号瞬态冲击特征的提取,并且相对于Teager能量算子的鲁棒性更好,误差更小,抗噪性能也更加强大。
2 1.5维谱与本文算法流程
2.1 1.5维谱
对于任意的平稳随机信号(),其三阶累积量可以表示为:

式中:[ ]表示数学期望。
令1=2=,即得到信号()三阶累积量的对角切片:

该对角切片的一维傅里叶变换即定义为信号()的1.5维谱():
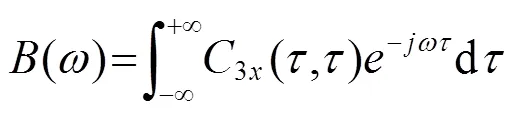
1.5维谱有一些很重要的性质,比如能够抑制高斯白噪声以及提取耦合谐波分量等[21],广泛的应用在非线性、非平稳信号的分析中。
2.2 本文算法流程
发电机运转时产生的振动信号是一种能量的载体,这种能量会在机组动力传动的过程中得以体现[22]。当发电机发生短路或者偏心等故障时,机组的一些零部件就会产生异常振动,而振动所传递的能量信息就会在时域或者频域发生突变。
由前面的分析可以得知,频率加权能量算子能够实现对信号故障特征的提取和增强,1.5维谱分析过程中也存在抑制噪声、提取耦合谐波分量的过程,两者联合,对故障特征振动信号进行二次抑噪及增强,实现本文的核心方法目的,对应的算法流程如图1所示。

图1 算法流程图
3 实验信号检测与验证
3.1 实验设备与方法
实验数据从新能源电力系统国家重点实验室MJF-30-6型隐极动模发电机组上进行测试获取,机组的基本参数见表1。
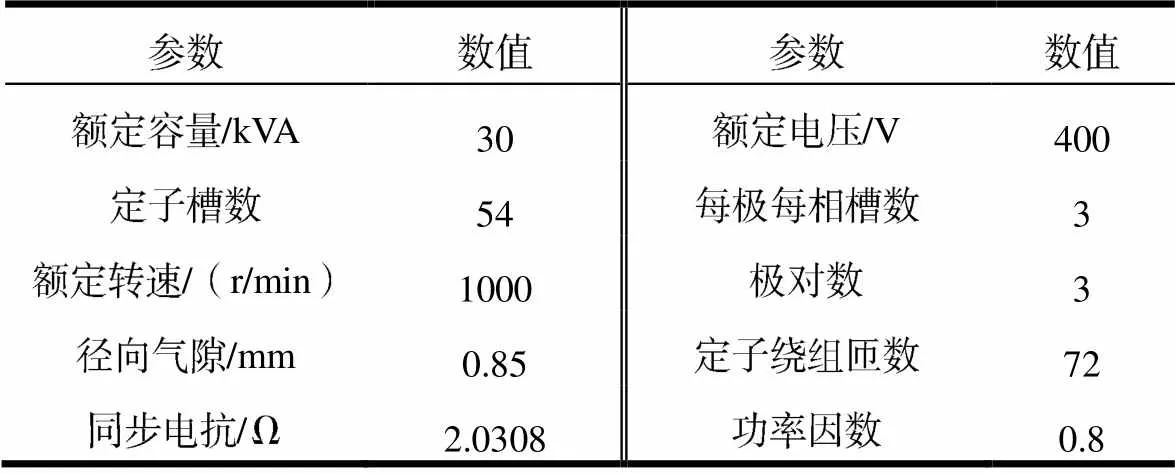
表1 MJF-30-6型隐极故障模拟发电机基本参数
实验通过安装在定子外圆面竖直方向的CD-21C型速度传感器(北京测振仪器厂生产,灵敏度为30mV/mm/s)测取定子匝间短路故障前后的定子振动数据,如图2所示,发电机定子和转子绕组分布如图3所示。
定子绕组匝间短路抽头设置为:在B相第一条支路和C相第一条支路各引出5个抽头,分别位于定子绕组相对中性点2%处(B11/C11)、5%处(B12/C12)、10%处(B13/C13)、20%处(B14/C14)、40%处(B15/C15);在C相第二条支路引出3个抽头,分别位于定子绕组相对中性点2%处(C21)、5%处(C22)、10%处(C23),共13个抽头,如图4所示。通过短接不同的短路抽头可以对不同程度的定子匝间短故障进行模拟。
实验中,发电机并网带500W负载运行,首先测取正常运行情况下的振动数据1作为对比;然后将定子绕组的C相第二条支路的C21和C22处短路,模拟3%定子匝间短路,获取故障数据2;再将定子绕组的C相第二条支路的C22和C23短路,模拟5%定子匝间短路,获取故障数据3。

图2 机组整体外观与传感器设置
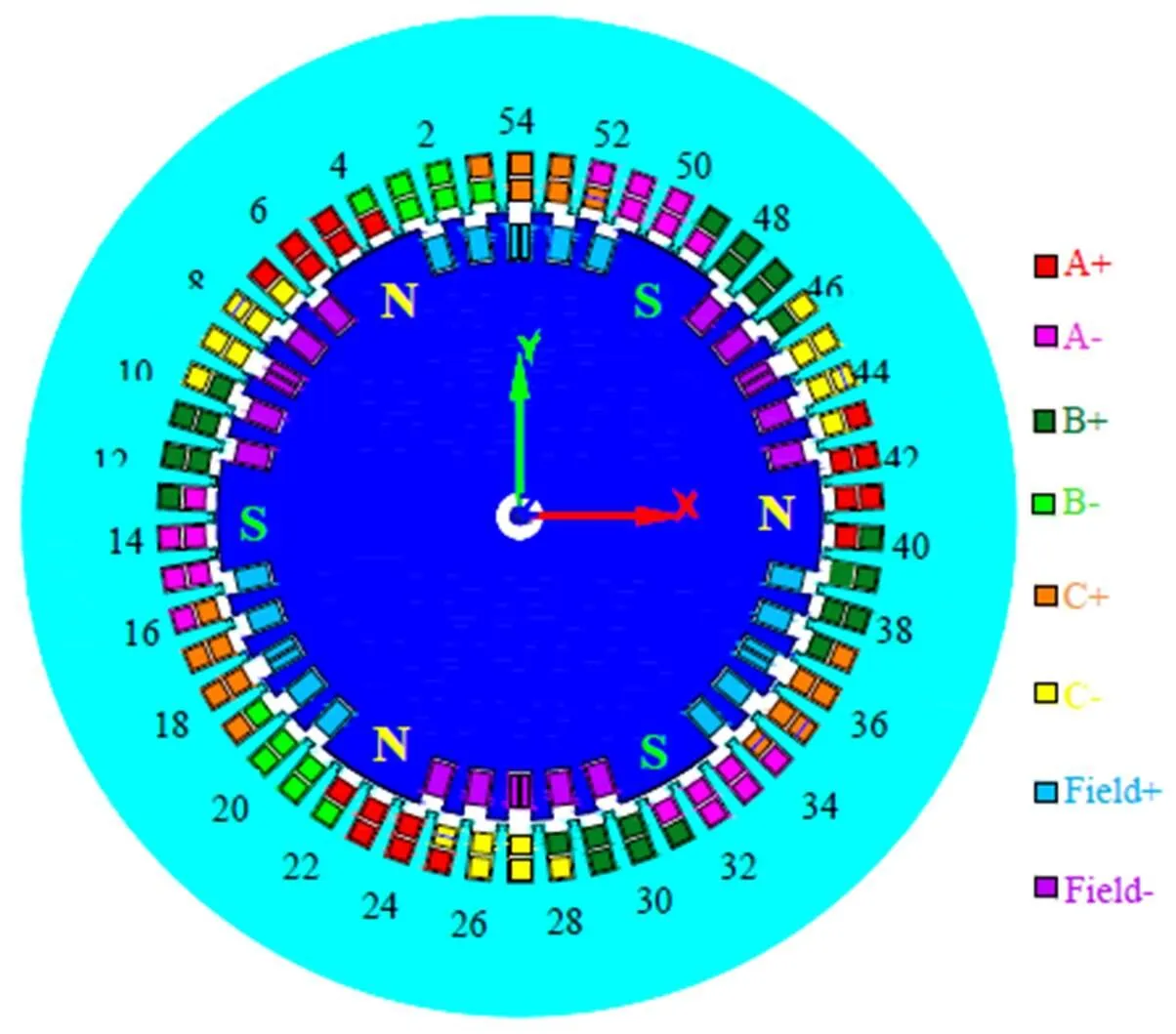
图3 发电机定子和转子绕组分布

图4 定子绕组匝间短路抽头
3.2 定子振动信号分析
对采集到的定子正常振动信号、3%定子匝间短路和5%定子匝间短路信号分别用最大相关峭度解卷积(MCKD)算法、1.5维包络谱、频率加权能量算子(FWEO)以及本文提出的频率加权能量算子结合1.5维谱的算法进行分析,原始信号以及经各算法处理后的结果分别如图5~7所示。
从图5(b)~图7(b)中可以看出,原始的定子振动信号含有较多的毛刺,频谱图较为杂乱,定子匝间短路故障下发电机定子振动的特征频率成分2、4、6完全被淹没,无法对发电机所处的故障状态进行诊断与识别。
图5(c)~图7(c)是对原始信号进行MCKD算法处理后的结果,处理过程中取值为100,优化后的取值为85,参数的详细设置求解过程可见文献[18]。由图中可看出,经MCKD处理后的频谱与原始信号相比有了较大改观,特征频率处的幅值有了一定的提升,说明MCKD算法可以有效增强多极电机的特征振动信号并达到滤噪效果。
图5(d)~图7(d)是对原始信号进行1.5维包络谱处理后的结果,可以看出,此算法可以有效的抑制噪声并增强各倍频成分的幅值,但对于2、4、6幅值的增强效果相对较为微弱,因此,单独采用1.5维谱达不到理想的增强效果。
图5(e)~图7(e)是对原始信号进行FWEO算法处理后的结果,频谱图中的谱线幅值在2、4、6这些故障特征频率处达到了较高的水平,相比MCKD算法的增强效果更明显,噪声等干扰信号的衰减也达到了比较满意的效果,因此,频率加权能量算子用来增强信号的故障特征是有效的。
图5(f)~图7(f)是本文算法处理后的结果,由图中可看出,本文算法最大程度地保留了原始信号的特征频率,噪声等干扰谱线很少,整个频谱较为干净利落,故障频率特征也较为明显。
对比文中提到的4种信号处理的方法可以看出,1.5维包络谱的效果最差,MCKD算法、FWEO算法及本文提出的FWEO结合1.5维谱的算法都能够实现对故障特征的增强,但是本文算法相比MCKD算法的特征频率幅值提升明显,相比FWEO算法的幅值也有一定的提升并且噪声得到了进一步的抑制。
虽然本文是对定子振动信号进行分析,但由于转子轴承座和定子固定在同一基础上,转子的振动会传递给定子,从而影响到定子的振动信号,例如转子的基频振动信号就会传递给定子,使得定子振动除了特征频率二、四、六倍频外在基频处也有较大的振动幅值。另外,由于本文实验的对象是三对极电机,受到谐波和电机齿槽效应的影响,导致了五倍频和六倍频处幅值较高[23]。处理后实验数据的整体结果基本符合定子匝间短路故障下所对应的振动特性。
为了更直观地将不同算法进行对比,将处理结果列表绘制成折线图,结果见表2和图8。因1.5维包络谱处理结果较差,在此未予列出。
由表2和图8可更直观地看出,本文算法的处理效果较为明显,特征频率成分与未处理信号相比有较为可观的增幅,与另外3种方法相比也有较明显的优势,说明本文所提出的频率加权能量算子与1.5维谱结合的方法在多极发电机特征振动信号的增强检测方面具有有效性和优越性。

图5 定子正常信号时域波形及不同方法处理后的频谱

图6 3%定子匝间短路时域波形及不同方法处理后的频谱
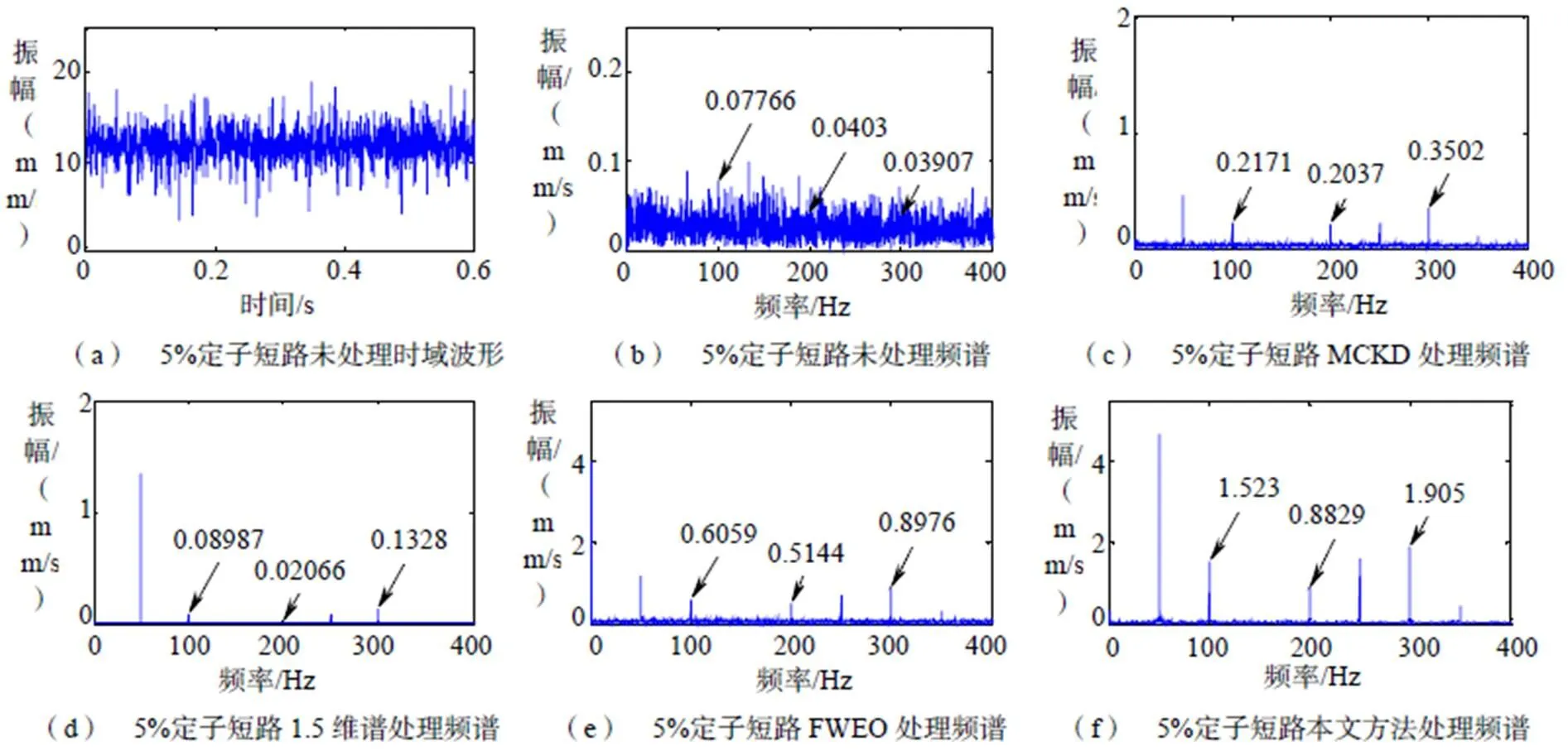
图7 5%定子匝间短路时域波形及不同方法处理后的频谱

表2 FWEO与MCKD算法处理结果对比

图8 正常、3%和5%定子匝间短路故障的处理结果对比
4 结论
本文提出了频率加权能量算子与1.5维谱结合的算法来处理多极发电机振动信号信噪比低、特征频率信号被淹没的工程问题。论文主要工作及分析结论如下:
(1)对多极发电机的原始振动信号进行了分析,发现未经特殊处理的多极发电机振动信号其频谱中的特征频率成分基本被淹没在噪声中,开发针对性的处理算法对多极发电机的特征振动信号进行有效增强并滤噪具有必要性。
(2)对三对极发电机定子匝间短路前后的定子振动信号分别进行了1.5维包络谱分析、频率加权能量算子(FWEO)算法分析和最大相关峭度解卷积(MCKD)算法分析,发现这些方法在一定程度上都能增强多极发电机的特征振动信号并达到滤噪的效果,综合处理效果为频率加权能量算子优于MCKD优于1.5维谱。
(3)采用本文提出的频率加权能量算子与1.5维谱结合的算法对三对极发电机故障前后的振动数据进行了处理并与其他算法结果进行了对比,发现本文算法在特征振动信号的增强和综合滤噪效果上要优于单一的频率加权能量算子算法、单一的1.5维谱算法,以及最大相关峭度解卷积算法。本文算法可有效提取多极发电机的故障频率特征,为故障识别与诊断提供便利。
[1] 何玉灵, 庞彬. 基于振动信号多尺度熵的发电机故障监测方法研究[J]. 电机与控制应用, 2015, 42(9): 43-46.
[2] 刘奎, 张冬梅, 于光, 等. 空气耦合超声信号的小波阈值滤噪试验研究[J]. 机械工程学报, 2015, 51(20): 61-66.
[3] 孙万麟, 山拜达拉拜. 多模噪声背景下基于遗传小波网络的滤噪研究[J]. 机械设计与制造, 2013(6): 190-192.
[4] 王晅, 张小景, 马进明, 等. Contourlet域中邻域窗最优阈值滤噪算法[J]. 计算机工程, 2010, 36(5): 223-224+227.
[5] 王芳, 卓莉, 李继红, 等. 基于粗集均值滤波的Hyperion高光谱数据滤噪方法[J]. 地理与地理信息科学, 2006, 22(6): 30-33.
[6] 胡寿松, 周川, 王源, 等. 基于小波神经网络的组合故障模式识别[J]. 自动化学报, 2002, 28(4): 540-543.
[7] 陆爽, 杨斌, 李萌, 等. 基于小波和径向基函数神经网络的滚动轴承故障模式识别[J]. 农业工程学报, 2004, 20(6): 102-105.
[8] 王冰, 李洪儒, 许葆华, 等. 基于数学形态学分段分形维数的电机滚动轴承故障模式识别[J]. 振动与冲击, 2013, 32(19): 28-31+92.
[9] Yanxue Wang, Jiawei Xiang, Richard Markert, Ming Liang. Spectral kurtosis for fault detection, diagnosis and prognostics of rotating machines: A review with applications [J]. Mechanical Systems and Signal Processing, 2016(66-67): 679-698.
[10] Libin Liu, Xihui Liang, Ming J. Zuo. Vibration signal modeling of a planetary gear set with transmission path effect analysis [J]. Measurement, 2016, 85: 20-31.
[11] Wangpeng He, Yin Ding, Yanyang Zi, Ivan W. Selesnick. Sparsity-based algorithm for detecting faults in rotating machines [J]. Mechanical Systems and Signal Processing, 2014, 72-73: 46-64.
[12] 周洋, 向阳, 黄陈哲, 黄进安. 基于VMD-SVD能量标准谱-Teager能量算子的轴承故障诊断方法[J]. 噪声与振动控制, 2019, 39(4): 212-217+253.
[13] 徐元博, 蔡宗琰, 丁凯. 复杂背景下对称差分解析能量算子在轴承故障诊断中的应用[J]. 振动与冲击, 2019, 38(8): 246-254.
[14] 安雪君, 郝如江, 史云林. 基于SK-CICA和Teager能量算子的滚动轴承故障诊断方法[J]. 轴承, 2018(10): 42-46.
[15] 马本栋, 胡书举, 孟岩峰, 宋斌, 吴涛. 基于多小波包-能量算子解调的滚动轴承复合故障诊断[J]. 噪声与振动控制, 2018, 38(4): 154-158.
[16] 万书亭, 李和明, 许兆凤, 等. 定子绕组匝间短路对发电机定转子径向振动特性的影响[J]. 中国电机工程学报, 2004, 24(4): 157-161.
[17] 何玉灵, 蒙玉超, 唐贵基, 等. 基于正弦结构元素的自适应Top-Hat变换及发电机特征振动信号增强检测[J]. 中国电机工程学报, 2016, 36(15): 4266-4273.
[18] 何玉灵, 王珂, 仲昊, 蒙玉超, 王晓龙, 唐贵基. 基于最大相关峭度解卷积算法的发电机特征振动信号增强检测[J]. 华北电力大学学报(自然科学版), 2017, 44(3): 67-73+89.
[19] 向天尧. 基于改进能量算子的滚动轴承故障诊断方法[D]. 湖南大学, 2017.
[20] O'TOOLE J M, TEMKO A, STEVENSON N. Assessing instantaneous energy in the EEG: a non-negative, frequency-weighted energy operator [C]//2014 36th Annual International Conference of the IEEE Engineering in Medicine and Biology Society. Piscataway, NJ, USA: IEEE, 2014: 5333-5342.
[21] 陈略, 訾艳阳, 何正嘉, 袁静. 噪声协助的EMD-1.5维谱信号抗混分解与特征提取[J]. 振动与冲击, 2010, 29(5): 26-30+237-238.
[22] 蒙玉超. 发电机故障的振动特征提取方法研究[D]. 华北电力大学, 2017.
[23] 王发林. 发电机气隙偏心与定子短路复合故障的转矩特性分析[D]. 华北电力大学, 2016.
Enhanced Characteristic Vibration Signal Detection of Generator based on Frequency Weighted Energy Operator and 1.5-Dimensional Spectrum
HE Yuling, SUN Kai, WANG Tao, BAI Jie
(Department of Mechanical Engineering, North China Electric Power University,Baoding 071003, China)
To overcome the shortage of low SNR (signal to noise ratio) of the multi-pole generator vibration signal which brings rigid difficulty to the fault diagnosis, a new method which combines the frequency weighted energy operator (FWEO) with the 1.5-dimentiaonal spectrum is proposed. This method uses FWEO to extract the shock features and remove the noise, while employs the 1.5-dimentional spectrum to enhance the characteristics vibration properties and filter the noise again. The application of this method to the 3 pole-pair generator before and after stator interturn short circuit fault validates the effectiveness of the method. Moreover, the comparison among the proposed method, the single FWEO, the single 1.5-dimentional spectrum, and the maximum correlation kurtosis deconvolution suggests that the proposed method is superior to these mentioned methods.
multi-pole generator; stator inter-turns short circuit (SISC); vibration signal; frequency weighted energy operator(FWEO); 1.5-dimensional spectrum
TM31
A
1000-3983(2021)01-0064-07
国家自然科学基金(51777074);河北省自然科学基金(E2020502032);中央高校基本科研业务费专项基金(2020MS114,2018YQ03);河北省青年拔尖人才支持计划([2018]-27)
2020-07-30
何玉灵(1984-),博士,研究方向大型发电机状态监测与故障诊断,副教授,硕士生导师。


