最佳子集多元线性回归模型在热带气旋风圈变化预报中的应用

饶晨泓 陈光华 陈可鑫 朱志伟

1 中国科学院大气物理研究所云降水物理与强风暴重点实验室，北京 100029

2 中国科学院大学，北京 100049

3 南京信息工程大学，南京 210044

1 引言

热带气旋（Tropical cyclone, TC）是地球上最具破坏性的天气系统之一，它会引起诸如风暴潮、台风浪、大风、强降雨等一系列灾害的发生，而西北太平洋（Westem North Pacific, WNP）又是全球TC生成数量最多、生成范围最广的海域之一（Elsberry, 2004）。WNP平均每年有 20多个 TC生成，约占全球TC生成总数的1/3（袁金南等,2008），而其中约1/4的TC登陆我国并造成严重影响，因此提高对TC特征指标预报的准确性将有利于提高沿海地区防灾减灾的能力，有助于保障人民的生命财产安全。

Holland and Merrill（1984）将 TC 的结构变化归为强度（intensity）变化、尺度（size）变化和壮度（strength）变化3种，其中，TC强度用 TC 风场的极大值表征；TC尺度用TC风场的水平范围表征，一般指七级风圈半径（最大风速半径外，径向风速衰减为17 m/s时距离TC中心的半径；记为R17，单位km）；R17范围内的区域称为内核，风场在内核区域的平均角动量为壮度。相较于TC的其他特征量，目前对TC尺度的研究相对较少，这主要是因为TC尺度的业务预报开展的时间较短，并且TC尺度的观测数据也较少。但是，对TC尺度进行研究却具有十分重要的意义，因为TC尺度可以提供TC灾害的面积，从而更好地预报TC的结构，为TC近海或登陆前后的防灾减灾工作提供帮助（吴磊, 2013）。

除了TC自身信息因子外，目前相当一部分研究工作也强调了大尺度环境场因子对TC尺度的影响 （ 李 崇 银 , 1983; 陈 联 寿 和 刘 式 适 , 1997;Khairoutdinov and Emanuel, 2013; Chavas and Emanuel, 2014; Chavas et al., 2016）。Liu and Chan

（2002）指出TC尺度变化与天气环流形势相关；Lee et al.（2010）进一步指出大部分的小尺度 TC形成于东风波内，而中到大尺度TC的形成常常与季风有关。Maclay et al.（2008）通过更高分辨率的飞机观测资料发现，影响TC尺度变化的主要物理过程与双眼墙替换和大尺度环境场的外部强迫有关，而环境强迫中最重要的因子是垂直风切变（VWS）。通过数值模拟，Wang（2009）强调了外围螺旋雨带潜热释放对TC内核尺度增长具有重要意义，因此他推测，TC内核尺度对相对湿度具有一定的敏感性。Hill and Lackmann（2009）基于位势涡度（PV）的观点也指出相对湿度对TC外围风场的扩展至关重要。Xu and Wang（2010）通过数值模拟进一步验证了相对湿度对TC内核尺度增长具有重要的意义。Lin et al.（2015）研究表明，TC 降雨区面积主要与相对海表温度（局地海表温度与热带平均海表温度之差）有关，而降雨量则随绝对海表温度的增加而增加。此外，200 hPa散度和850 hPa涡度可表征大尺度环境强迫场对TC的影响，200 hPa等压面上的温度可表征TC环流高层流出层的温度（Lee et al., 2015）。在前人研究的基础上，本文综合考虑了TC自身信息和大尺度环境场因子对R17的影响，在TC的生命周期中，研究R17的变化情况，并对R17的变化趋势及大小进行预报。

建立统计学模型是TC特征参数预报的重要手段之一。多元线性回归模型在对TC强度的预报研究中已得到应用（Neumann, 1972; Jarvinen and Neumann, 1979; Chu, 1994）。金龙等（2008）选择复共线性关系小的预报因子组合利用逐步回归方法预报台风移动路径。从理论上讲，逐步回归只选出了一个局部最优子集，但是这个子集不一定是所有子集中最优的。此外，逐步回归方法在每一次回归时都引进方差贡献最大的那个因子，这种标准往往会导致选择过多的因子，从而使预报效果不稳定。为了避免逐步回归方法的弊端，Demuth et al.（2006）将Miller（2002）提出的最佳子集多元线性回归方法运用于TC强度的估计，当有n个备选因子时，所有可能的回归模型共有2n−1个，当满足1）所有因子通过95%信度水平、2）平均绝对误差（MAE）最小时，则该因子组合为最佳子集因子组合。为了保证结果的显著性，他还对每个可能的回归方程进行了交叉验证。

本文将尝试运用最佳子集多元线性回归方法研究TC R17的变化，对R17的两个预报量的变化趋势及大小进行预报。规定观测记录当前时刻为初始时刻，两个预报量分别为：未来12小时R17的大小（R17_12）和未来24小时R17的大小（R17_24）。对于预报因子的选择，本文综合考虑了TC自身信息（位置、强度）及大尺度环境场因子（热力学因子、动力学因子、水汽因子）对R17的影响，以进一步提高对TC R17变化趋势及大小预报的水平。

2 数据与方法

2.1 数据

2.1.1 数据的来源

本文所用的TC数据来自第四代最佳路径（ International Best Track Archive for Climate Stewardship， IBTrACS） 数 据 集 （ Knapp et al.,2010），具体为 TC中心的纬度（LAT）、经度（LON）、最大持续风速（MSW）、最低海平面气压（MSLP）、离岸距离以及4个象限（东北NE、东南SE、西南SW、西北NW象限）的R17（R17_NE、R17_SE、R17_SW、R17_NW）。将西北 太平 洋 上 （ 0º～ 40ºN， 140ºE～180º） 2001～2015年6～11月的数据作为研究数据，时间分辨率为 6 h，即在 00:00（协调世界时，下同）、06:00、12:00、18:00各有一次观测记录(https://www.ncdc.noaa.gov/ibtracs/[2020-03-10])。

大尺度环境场数据来自欧洲中期天气预报中心（ European Centre for Medium-Range Weather Forecasts，ECMWF）的再分析（ERA-Interim）数据，具体为925 hPa、700 hPa的比湿，海表温度，850 hPa、200 hPa 的风场，200 hPa 的散度，850 hPa的相对涡度以及200 hPa的温度。时间、空间的范围和及时间的分辨率同TC数据，水平分辨率为0.75º（纬度）×0.75º（经度）(https://www.ecmwf.int/en/forecasts/datasets/reanalysis-datasets/era-interim[2020-03-10])。

表1 10个预报因子的简称、单位与描述Table 1 Abbreviations, units, and descriptions of the ten predictors

2.1.2 物理量的计算

本文综合考虑了TC自身信息因子以及大尺度环境场因子对TC R17变化的影响，选取的10个预报因子及其具体描述如表1所示，其中LON、LAT、MSW、MSLP直接来自IBTrACS数据集，6个大尺度环境场因子的计算方法如下：首先，寻找距离TC中心最近的ERA-Interim格点作为极点建立极坐标系，每隔45º方位角取一条极坐标半径；然后，取海表温度的径向格点分辨率为0.1º，剩余5个大尺度环境场因子的径向格点分辨率为1º，将ERA-Interim格点数据插值到极坐标网格中；最后，对于 925 hPa、700 hPa 的比湿，850 hPa、200 hPa的风场，200 hPa的温度，为了去除TC环流对环境场的影响，取TC半径2º～7º之间的圆环区域，对于200 hPa的散度，850 hPa的相对涡度，取TC半径9º以内的圆形区域，对于海表温度，取TC半径0.5º以内的圆形区域，计算极坐标系中不同区域的平均值（DeMaria and Kaplan, 1994; Maclay et al.,2008; 梅双丽和江静, 2012）。

平均比湿（Q）定义为

其中，q925、q700分别表示 925 hPa、700 hPa 高度场上TC半径r=2º～7º范围内的区域平均湿度。

在前人的研究中VWS有多种定义方法（Gray,1968; 陈联寿和丁一汇, 1979），本文采用了 Palmer and Barnes（2002）求取VWS的方法，将VWS定义为

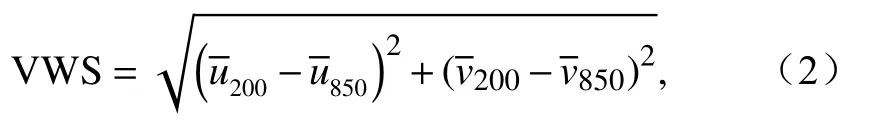
2.2 方法

考虑到不同初始尺度的TC存在较大的个体差异，为了使回归结果具有更强的针对性，本文按照初始尺度的大小将TC分为4类，针对每类中单个TC的各预报量运用最佳子集多元线性回归方法。该方法将遍历n个预报因子所有可能的组合并建立回归方程，例如n=3，将产生2n−1=7个多元线性回归方程：3个包含1个预报因子、3个包含2个预报因子和一个包含3个预报因子的回归方程。通过一定的标准，分别在4类中挑选最优因子组合建立最佳子集的多元线性回归方程。

我们挑选预报因子的标准是基于F检验以及各种因子组合建立回归方程所产生的MAE，具体步骤如下：首先，对每个TC所记录的R17数据与10个预报因子的不同组合之间分别建立回归方程，确定方程系数，并对各预报因子进行F检验。然后，通过计算不同因子组合的回归方程的MAE来考察回归效果。为了得到每个TC每种因子组合方程更加稳定的MAE，我们在计算MAE时采用了5-折交叉验证的方法，具体步骤如下：假设第g（g≤4）类中共有Kg个TC，对于每个TC都有210−1=1023种因子组合方式，计算第m种因子组合方程的MAE时，1）由于采用5-折交叉验证，因此将预报量和预报因子的所有数据大致均分为5组；2）分别选取其中第i（i≤5）组作为测试组，剩余4组作为训练组，利用训练组的样本数据进行拟合，得到针对第i个测试组的回归方程，接着利用测试组的样本数据计算回归方程的平均绝对误差（MAE(g,k,m,i)，其中g、k、m、i分别表示第g类的第k个TC、第m种因子组合、第i个测试组）；3）根据如下公式：

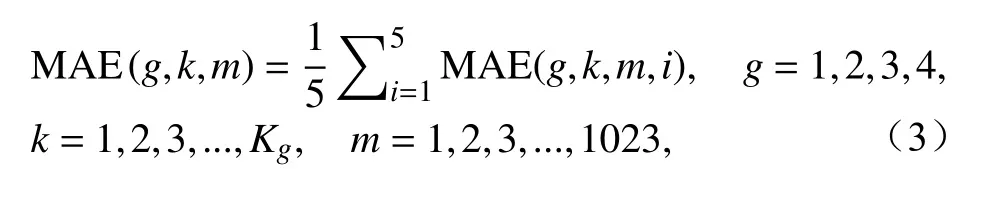
计算5个测试组mae(g,k,m,i)的平均值作为第g类的第k个TC第m种因子组合方程的MAE(g,k,m)。最后，对于第g类第m种因子组合，计算Kg个TC中预报因子全部通过95%信度水平（F检验）的回归方程对应的MAE的平均值MAE(g,m)，选取MAE(g,m)中最小值所对应的因子组合作为第g类TC的最佳子集因子组合。

2.3 数据处理

2.3.1 预报因子和预报量数据的筛选

根据GB/T 19201～2006《热带气旋等级》国家标准，将TC按照MSW的大小分为热带低压（TD）、热带风暴（TS）、强热带风暴（STS）、台风（TY）、强台风（STY）和超强台风（SuperTY）6个等级。本文只选用强度大于TS级别，即MSW≥17.2 m/s的TC观测记录作为研究对象。Knaff et al.（2016）对两个路径不同的TC进行研究后发现，当TC登陆后，地形的分布差异将给TC风场结构不对称变化带来不同的影响，为了减小地形对TC风场结构的影响，本文只对位于海上的TC R17的变化进行研究，即筛选离岸距离≥500 km的TC。在 Demuth et al.（2004）的研究中，R17 取 R17_NE、R17_SE、R17_SW、R17_NW的平均值，包括了那些不存在风半径的象限。为了降低通过象限平均得到的R17数据的噪音，本文去除了存在风半径缺测的TC观测记录，同时也避免了R17计算值偏小的现象。

将WNP上2001～2014年6～11月的数据作为训练样本，2015年6～11月的数据作为测试样本。为了提升回归的效果，本文还对预报因子和预报量数据进行了质量控制：1）删除训练样本与测试样本中存在缺测值的观测记录；2）将训练样本与测试样本中各预报因子和预报量数据分别按照升序排列，删除小于第1个百分位点和大于第99个百分位点的极端观测记录；3）删除训练样本中观测记录数量少于20个的TC，删除测试样本中观测记录数量少于10个的TC。经过筛选后，训练样本和测试样本中，对R17_12进行预报时的TC个数和观测记录数量大于或等于对R17_24进行预报时的TC个数和观测记录数量（表2）。

表2 预报R17_12和R17_24时训练样本和测试样本中符合筛选条件的TC个数及观测记录数量Table 2 Number of TCs and observation records in the training set and test set that matched the screening conditions when forecasting R17_12 and R17_24

2.3.2 预报因子与预报量相关性的考察

本文基于前人研究，考虑了TC自身信息以及大尺度环境场对R17的影响，选取了10个预报因子，并进一步考察了这些预报因子与预报量之间的相关性，以确保在构建回归模型时能取得较好的回归效果。预报因子与预报量之间相关性的衡量方法如下：1）当预报某一预报量时，在第k个TC（共K个TC）的生命周期中，分别计算每个预报因子与预报量的相关系数rkd（k=1,2,...,K，d=1,2,...,10；rkd表示第k个TC的第d个预报因子与预报量的相关系数）；2）对于第d个预报因子，计算K个TC中通过95%信度水平（t检验）的相关系数绝对值的平均值。从图1中可以看到，所有的值均大于0.5，说明这10个预报因子与R17_12和R17_24之间的相关关系较好，对预报量的变化具有一定的影响。

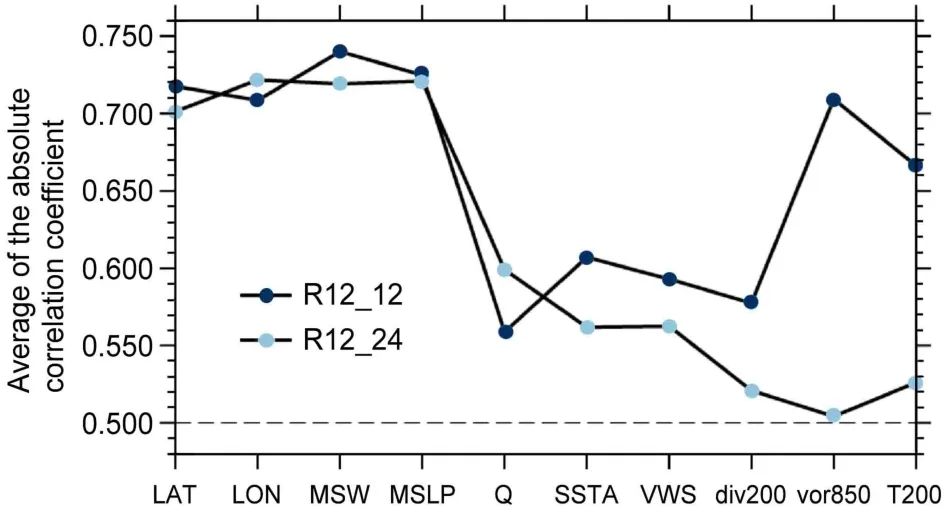
图1 预报R17_12和R17_24时各预报因子与预报量相关系数绝对值的平均值Fig. 1 Average of the absolute correlation coefficient between each predictor and predictand when forecasting R17_12 and R17_24

3 模型构建

除了大尺度环境场因子和TC自身信息外，前人的研究中（Cocks and Gray, 2002; Xu and Wang,2010）还强调了初始涡旋大小对TC尺度的影响，因此本文根据TC初始涡旋尺度对TC进行分类，从而得到针对不同初始涡旋尺度的某一类TC的最佳子集多元线性回归（bs-MLR）模型。将经过2.3.1筛选后，TC观测序列中的第一个R17作为此TC的初始尺度（R17_0），将R17_0按照升序排列，分别以R17_0的第25个、第50个、第75个百分位点作为分界阈值，将TC分为4类。分类结果如表3所示，预报R17_12和R17_24时，R17_0的第25个、第50个、第75个百分位点分别对应为92.6 km、111.1 km、138.9 km。

在4个分类中，针对各类TC的各预报量运用最佳子集多元线性回归方法，得到各类TC的最佳子集因子组合；然后，将各类中所有TC的最佳子集因子组合方程对应的系数求平均，确定出不同R17_0分类时针对某一预报量的回归方程。由表4可知，各类TC回归方程的最佳预报因子个数在2～5个左右，因子数目较少，可有效避免预报效果不稳定的现象发生。

4 结果分析

得到了针对不同R17_0、不同预报量的回归方程后，本文选取了2015年6～11月的全部11个TC（观测记录数量大于10个的TC）：Chan-hom、Nangka、 Halola、 Soudelor、 Goni、 Atsani、 Kilo、Krovanh、Dujuan、Champi、In-fa，对bs-MLR 模型的预报效果进行检验。分别用MAE、符合指数（d）和相关系数（R）的大小来评估bs-MLR模型对于预报量的预报情况（表5）。符合指数d用Willmott（1982）提出的值位于0～1之间的无量纲数表示，d的值越大表示符合程度越高，公式如下：

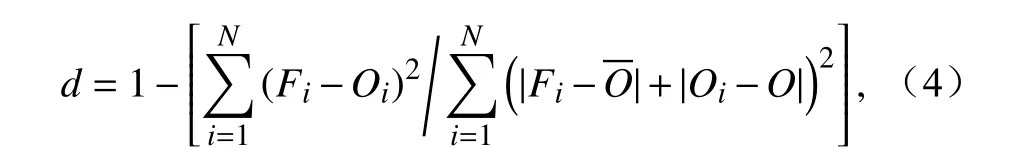
其中，Fi表示第i次预报值，Qi表示第i次观测值，表示观测平均值，N为单个TC的观测记录次数。

表3 预报R17_12和R17_24时的分类情况及观测数量Table 3 Categories of R17_12 and R17_24 with their observed numbers

表4 预报R17_12和R17_24时各类TC的回归方程Table 4 Regression equations of each TC category when forecasting R17_12 and R17_24

表5 测试样本误差分析Table 5 Error analysis of the test set

由表5可知，当预报R17_12时，4类TC的预报效果不同。其中预报效果最好的是第三类TC，Soudelor和Goni的R值分别为0.90和0.86，d值分别为0.82和0.55，说明该类TC的回归方程不仅对R17_12变化趋势的预报效果较好，对于R17_12的大小也具有一定的预报能力。其次，第一类TC的预报效果也较好，Chan-hom、Nangka和Halola的R值分别为0.89、0.61、0.91，说明该类TC的回归方程对R17_12的变化趋势具有一定的预报能力，其中Chan-hom和Nangka的MAE分别为33.94 km和56.78 km，和其他TC相比值较小，d值分别为0.86和0.77，说明该类TC的回归方程对于R17_12的大小也具有一定的预报能力。对于第二类TC，Atsani的R值为0.68，d值为0.56，但是Krovanh的R值未通过95%信度水平，并且d值仅为0.16，因此该类TC的回归方程对R17_12的变化趋势和R17_12的大小的预报能力较差。对于第四类TC，Kilo和Dujuan的R分别为0.76和0.93，d值分别为0.62和0.57，但是Champi和In-fa的R都未通过95%信度水平，并且d值都较小，因此该类TC的回归方程对R17_12的变化趋势和R17_12的大小的预报能力也较差。总体来说，运用bs-MLR模型对R17_12进行预报时，R17_0小于92.6 km和R17_0位于 111.1～138.9 km之间的 TC，回归方程对R17_12变化趋势的预报效果较好，对R17_12的大小具有一定的预报能力。

当预报R17_24时，4类TC的预报效果与预报R17_12时有所不同。对于第三类TC，Soudelor和Goni的R值分别为0.82和0.65，虽然Soudelor的d值为0.82，但是Goni的d值仅为0.34，说明该类TC的回归方程对R17_24的变化趋势具有一定的预报能力，但是对R17_24大小的预报能力较差。对于第一、二、四组TC，每一类中皆存在1个TC的R未通过95%信度水平，因此这些TC的回归方程对R17_24的变化趋势的预报能力较差，并且每一类中至少存在1个TC的MAE较大，d值较小，因此这些TC的回归方程对R17_24的大小的预报能力也较差。总体来说，运用bs-MLR模型对R17_24进行预报时，R17_0位于111.1～138.9 km之间的TC，回归方程对R17_24的变化趋势具有一定的预报能力，但是对R17_24的大小不具有预报能力。

通过对比R17_12和R17_24的预报效果可以发现，预报R17_12时，可对两类TC的变化趋势和大小进行预报；而预报R17_24时，却只能对一类TC的变化趋势进行预报，R17_12的预报效果优于R17_24的预报效果，说明预报时效越短，趋势预报的准确性越高。

5 结论和讨论

本文运用最佳子集多元线性回归方法，针对2001～2014年6～11月WNP上强度大于TS级别的 TC，选取 LAT、LON、MSW、MSLP、Q、SSTA、VWS、div200、vor850、T200这 10 个预报因子，对于不同R17_0的各类TC构建bs-MLR模型。首先，以TCR17_0的第25、50、75个百分位点作为分界阈值，将所有TC分为R17_0不同的4类；然后，针对各类TC的各预报量运用最佳子集多元线性回归方法，得到各类TC的最佳子集因子组合；最后，将各类中所有TC的最佳子集因子组合方程所对应的系数求平均，确定出不同R17_0分类时针对某一预报量的回归方程。利用2015年的11个TC对各组回归方程的预报效果进行检验。研究结果表明：1）bs-MLR模型对R17_12进行预报时，R17_0小于 92.6 km 和R17_0位于 111.1～138.9 km 之间的TC，回归方程对R17_12变化趋势的预报效果较好，对R17_12的大小具有一定的预报能力；2）bs-MLR模型对R17_24进行预报时，R17_0位于111.1～138.9 km之间的TC，回归方程对R17_24的变化趋势具有一定的预报能力，但是对R17_24的大小不具有预报能力；3）预报时效越短，预报的准确性越高。

在未来的研究中，可以考虑将最佳子集多元线性回归方法结合动力模式进行动力统计预报，但是目前还有一些因素制约着最佳子集多元线性回归方法预报的准确性，比如：1）是否还存在更合理的TC的分类指标；2）影响WNP TC R17变化的因素有很多，是否存在更重要的预报因子未被选入，是否存在重要的物理过程未被考虑；3）本文的研究方法是否适用于TC强度变化、频数预报等其它特征参量的研究，这些都需要未来更近一步的研究。