气液两相流管道泄漏流场特性数值模拟分析

纪 健，傅晓宁，王 毅，李俊飞，纪宝强

(1.东华理工大学土木与建筑工程学院，南昌 330000；2.中国石油新疆油田分公司，克拉玛依 834000)

目前关于气液两相流声场的研究和模拟几乎空白，气液两相流管道流动的复杂性导致模拟存在很大误差。国内外关于气液两相流场与声场研究主要基于实验分析，但实验条件下能测量的参数很有限。通过数值模拟分析泄漏过程各个参数变化，补充实验在描述各流场参数方面的不足。水平管道的气液两相流的流场噪声产生原因是两相流中的气液持液率变化、湍流产生的压力脉动和速度脉动，因此分析水平管道气液两相流压力和速度变化有助于对气液两相流声场特性的掌握。

通过泄漏开启过程参数变化分析三种流型工况下泄漏过程的声波特性，即数值模拟的目的就是分析不同流型下气液两相流管道泄漏工况下的流场参数，主要包括管道发生泄漏前后，泄漏孔处压力、流速、湍流强度、涡量等流体参数变化，进而分析各流型工况下的泄漏发生时的流体发声机理。

1 模型选择、计算方法和边界条件

多相流流体控制方程和数学模型：计算流体力学软件通常采用纳维-斯托克斯方程作为控制方程对气液两相流管道进行数值模拟[1-5]，其连续性方程、动量守恒方程和能量守恒方程为

(1)

(2)

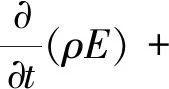
(3)

式中：ρ为气体密度，kg/m3；u为气体速度，m/s；p为气体静压，kPa；τij为黏性应力张量；E为总能，J；qj为热通量，J/s；t为时间，s。

数值模拟软件常用湍流求解的方法很多，相关研究成熟。文献调研对比分析发现[6-11]，Realizablek-ε模型可以在强流线弯曲、旋涡和旋转方面表现很好，且在预测流动分离和复杂二次流、圆形射流等方面模拟效果极好，因此选择其作为湍流模型[12]，进行湍动能、耗散率输运和湍流黏度计算。

计算流体力学提供的三种最基本多相流模型是Mixture模型、Eulerian模型和VOF(volume of fulent model)模型[13-16]，各个模型技术成熟，均得到广泛应用和深入研究。模拟的主要目的是研究气液两相管内泄漏前后流动形态和气液两相界面不断变化。VOF模型是基于求解体积分数方程来实现准确追踪气液两相流的界面变化情况的，主要适用于有明显气液相间界面的流动模拟。因此选择VOF模型瞬态求解，气液两相界面相互作用方法采用几何重构格式，其表面张力采用连续表面力模型[17-18]。

水平气液两相流动过程中绝热，气体可压缩，液体不可压缩。设空气为主相，水为次相。模拟和实验条件均为低压系统，气体符合理想气体状态方程。水平管道中的流动状态具有强瞬态特性，计算过程用压力的隐式算子分割法(pressure implicit with splitting of operators，PISO)算法，时间步长选取1×10-6s。

计算模拟过程，监控球阀模拟泄漏过程中的泄漏孔处的升力系数随时间变化，以及泄漏孔处的动态压力变化。稳定条件需要满足保障检测点参数波动变化曲线稳定以及基本的气液两相流动模拟收敛条件。设计入口边界条件利用实际流动参数计算获得。气液入口设为与实验过程相对应的质量流量入口，出口设置为压力出口。

2 几何模型、网格划分、泄漏方式

依据实验建立泄漏仿真模型依据前期实验管道完成，由主管道和泄漏模拟分支管道组成，原理是利用一个T形支管安装球阀，通过开启球阀并更换泄漏孔径的方法模拟各种工况泄漏，主管道参数与实验相同，管径37 mm、管长1 200 mm；泄漏模拟分支管道管径10 mm、管长120 mm。主管道和分支管道中心线交点定义为原点。泄漏管道球阀的球芯中心位置为直角坐标(0，80)处，孔板壁厚2 mm，泄漏孔径选取6 mm，气体从主干管道左端流入，从主干管道右端流出，具体尺寸方位如图1所示。

图1 简化的管道泄漏几何模型Fig.1 Simplified geometric model of pipeline leakage

网格生成直接关系到计算问题的成败，对数值模拟计算至关重要。网格主要分为结构网格和非结构网格两大类。结构化网格是只包含四边形或者六面体，非结构化网格是三角形和四面体。对于二维模拟，选用四面体网。针对水平管道流动特性和几何形状的复杂程度，同时考虑计算精度，时间耗费等问题，采用以下策略进行网格划分：整体采用结构网格，气液入口处两相相互混合，速度梯度较大，泄漏支管管道流线发生大角度弯曲，且管道结构本身具有细长特点，为实现泄漏流场和声场的转换的准确，对气液入口和泄漏支管上、主分支管道的相交处网格进行加密。依据以上策略得到两种几何模型的两种网格数量分别为网格1和网格2，分别为25 368和64 000。对两种不同密度的网格的计算结果进行对比，选取泄漏开启过程压力参数作为敏感性分析的特征参数，结果图2所示，两种网格质量的计算结果非常相近。因此充分考虑计算精度要求和效率，选定网格1进行数值模拟。

图2 两种不同网格相应的压力变化曲线Fig.2 Pressure change cuver of two different meshing

利用动网格计算需要在用Gambit中进行网格划分时，对阀芯与泄漏管道边界设置如图3所示。

图3 几何模型的网格划分和边界设置Fig.3 Structured mesh of geometries and boundary setup

图4 泄漏模拟球阀阀门转动规律Fig.4 Rule of valve rotation of leakage simulated ball valve

在实际工程中管道发生泄漏是在瞬间完成的。采用Fluent中动网格技术模拟泄漏并定义阀门开启时间设置[19]。假设阀门位移与时间关系如图4所示，时间t时刻阀门开启，阀门开启时间为0.1 s，保持开启状态直至流动稳定。

3 数值模拟结果分析

重点分析泄漏导致水平管道内气液两相流场内的总压力、流速、湍流强度和涡量这四个流动参数量的变化情况。为了更好地对比分析不同流型下泄漏对流动的影响，选择实验过程中三种流型对应气液折算速度下的气液质量流量数据，如表1所示。

表1 各流型模拟数据选取Table 1 Selection of flow pattern simulation data

以实验模型为研究对象，进行气液两相流水平管道上部泄漏流场模拟。以表1中分层流对应气液质量流量设置气液入口边界，泄漏孔径6 mm为例，进行球阀转动过程流场的数值模拟。气液混合速度矢量变化如图5所示，该云图代表气液混合速度的大小，各图依次为球阀转动间隔0.01 s的气液速度变化，即从球阀开始转动到完成转动的各个0.01 s时间的球阀开启不同程度的速度变化。由图5可以得到以下结论。

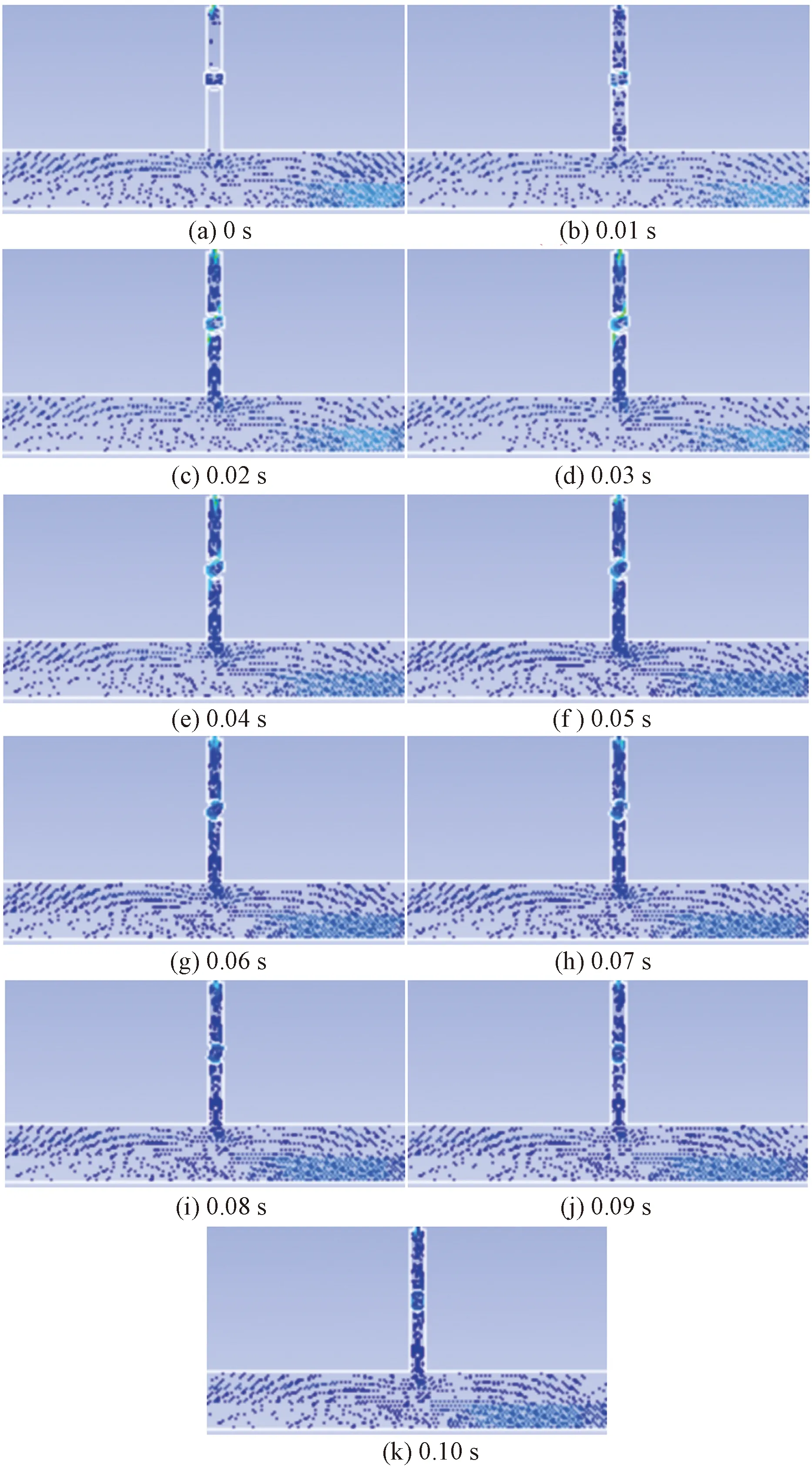
图5 不同时刻流体速度矢量图Fig.5 Vector diagram of fluid velocity at different times

(1)当管道内流动状态为分层流时，球阀的转动从开启到完成整个过程，上部泄漏支管道内流体为气体，几乎没有液体存在。泄漏气体瞬时充满整个分支管道。气体喷射出管道通常发生在球阀旋转的第0.01秒稍后，球阀在第0.01秒才能实现真正意义的开启。

(2)泄漏阀门真正开启时，泄漏流体在阀门出口处形成高速流动，空气突然膨胀、减速、扩张或碰撞产生雷诺应力或剪切应力形成湍流导致空气动力发生。存在某一时间段，支管道中的泄漏流体流动速度大于主管道中的流体流动速度。主管内的液体需要克服重力作用才能被气体携带出泄漏管道，通常情况需要较高的气体流速。

球阀开启前，管道内处于稳定流动，主管道和分支管内的气液均处于相对稳定的状态。球阀开启瞬间，由于球阀内的压力远小于支管道内球阀前的压力，在内外在压差的作用下，气体迅速流入球阀，泄漏支管中流体的速度瞬间增大。随着球阀继续转动，气体流入支管道，并随着球阀的不断开启，气速不断增大。此时实验过程流体动力学特性和数值模拟分析结论相同。数值模拟泄漏时，在球阀的开启过程进行泄漏孔口的升力系数Cl监测。Cl是由监测点所受升力除以参考值计算的动压得到，由升力系数定义得知其为无量纲量。

稳定流动时，分支管道泄漏孔口升力系数为零。模拟泄漏过程，球阀开启动作定义发生在0.5～0.6 s内，即图4中t=0.5 s。球阀球芯开始转动，但阀门并没有实现实际性的开启，即图3中交界面还不存在，此时升力系数仍然为零。当随着球阀的继续转动，球阀实现真正开启。得到各个流型球阀模拟泄漏过程中的泄漏孔口处升力系数Cl随时间变化曲线如图6所示。

图6 泄漏孔升力系数随时间变化Fig.6 The lift coefficient of leakage hole changes with time

分层流、波浪流、段塞流泄漏模拟在球阀开启过程，即球芯发生转动过程中，各个流型工况下升力系数均发生了极大变化，区别于泄漏发生前均趋于水平为零值，极容易分辨识别，与理论分析相一致，即泄漏孔口处由无任何流体通过时不受任何作用力；而阀芯转动，当有流体流入分支管道，泄漏孔口开始受到力的作用，此时升力系数发生变化。对比分析图6升力系数Cl随着流型从分层流、波浪流、段塞流依次变化，其各自流型下的升力系数最大值不断增大。与理论分析相同，即升力系数与流体的动压有关，动压越大其绝对值越大。通过球阀的阀芯转动实现开启在模拟过程只发生一次，与实际工况相符，为非周期性。

4 数值模拟与实验验证

结合模拟设定，升力系数即为泄漏孔处受到的升力除以参考值计算得到的泄漏孔口处的动压。此时最小升力系数与实验过程泄漏发生时刻产生的最小动态压力幅值相对应。在各个流型下分别对应的最小升力系数Cl变化曲线和最小动态压力信号p变化曲线之间存在一个关系为:Cl/p=常数。若两者间的关系成立可以证明泄漏过程数值模拟符合实验。通过图6数值模拟结果数据分析，得到最小升力系数值。

由表1实验数据选取对应各个流型工况下气液流量模拟泄漏，泄漏孔径为6 mm采集到相应各个流型下的动态压力信号，得最小升力系数和最小动态压力值如表2所示。分别对表2中最小升力系数和最小动态压力幅值离散点进行相关性验证，得到升力系数和动态压力变化拟合曲线和相关系数，如图7所示。

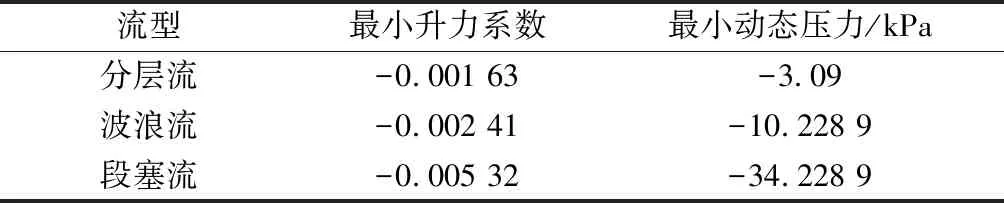
表2 球阀开启模拟与实验过程参数对比Table 2 Comparison of simulation and experimental process parameters of ball valve opening

图7 数值模拟升力系数和实验动压拟合关系曲线Fig.7 Fitting curve of lift coefficient of numerical simulation and experimental dynamic pressure

拟合得到相关系数为R2=0.999 7，说明两者之间具有很好的相关性，且由此可得Cl/p=0.000 1，即泄漏模拟开启过程得到的数值模拟结果与泄漏实验结果相符合。

5 泄漏开启过程参数分析

5.1 分层流泄漏开启模拟参数分析

分析分层流泄漏开启流场，首先数值模拟4 mm和6 mm泄漏孔径时泄漏开启过程，流场分析得总压力、流速、涡量、湍流强度变化如图8所示。

图8 分层流泄漏模拟过程每0.01 s各参数变化曲线Fig.8 Simulates the variation curve of each parameter every 0.01 s in the leakage process of stratified flow

其中，球阀转动0.1 s内的每间隔0.01 s采样保存一次，共采集11个点的参数变化。采样点1为球阀球芯即将发生转动，采样点11处为完成球芯转动，球阀开启过程完成。由图8分析发现各参数变化具有以下特点。

由图8(a)发现，球阀真正开启过程瞬间为图中第2个采样点，即第0.01 s处，此时总压力曲线出现最大值，说明球阀真正转动开始瞬间管道内的总压最大，此时泄漏瞬时声波信号幅值最大，即管道内的气体从阀芯连通支管部分向外泄漏，泄漏孔径越大，瞬时声波信号越强烈，波动幅值越大。

由图8(b)发现，在第0.01 s处为开启过程流体流速变化曲线的最小值点。流速在开启瞬间迅速减小到最低，然后随着球阀的转动时间增长再逐渐增加。出现这种现象的原因，同理第一个采样点没有泄漏发生，此时刻泄漏前最后稳定流动时刻，此时的管道内流体流动最大值仍然出现在主管道，该值为主管道内最大气液流速。泄漏发生在泄漏孔发生相分离，主管道和分支管道出现气液重新分配，主管道减小而分支管的流速增加，压力势能还未完全转换为流体动能。随着球阀球芯转动，越来越多气体流入分支管道，球阀完全开启后泄漏流体流速到达最大。随泄漏孔径增大，泄漏流体流速增大。

由图8(c)发现，涡量在球阀开启过程呈波浪式变化。球阀开始转动时先增大后减小，然后又增大再减小直到开启完成，变小趋于稳定。整个过程涡量具有两个极大值，说明在球阀的开启过程中，球阀先造成流体扰动引起涡量发生很大变化，而流体又与管壁相互作用，造成涡量不稳定。随着球阀开启的完成，分层流涡量大小恢复到泄漏前大小，此时泄漏孔径对涡量影响不大。由理论分析知涡量主要产生偶极子声源，球阀开始转动前几个采样点造成管道内流场产生涡量很大。

由图8(d)发现，随着球阀开启，管道内湍流强度不断减少，该最大湍流强度值通过分析发现通常出现在管道出口处，在分层流上部泄漏时泄漏流体只有气体喷射，说明在球阀开启的瞬间湍流强度最大，此时湍流噪声作为产生四极子声源是分层流泄漏瞬时声波产生的主要原因之一。

分层流管道阀门球芯开始转动，连通分支管瞬间，管道内的压力最大，内外压差最大，此时气液泄漏流体流速最小。球阀开始转动，附近产生的流体总压、涡量、湍流强度变化出现最大值，说明分层流泄漏声波信号主要产生于球阀开启瞬间。分层流泄漏声源组成主要为偶极子声源和四极子声源。随着泄漏孔径增大，球阀开启过程的最大压力和流速值增大，涡量和湍流强度的变化剧烈程度增加。

5.2 波浪流泄漏开启模拟参数分析

同理，分析波浪流泄漏流场，各参数最大值变化如图9所示，分析发现各参数变化具有以下特点。

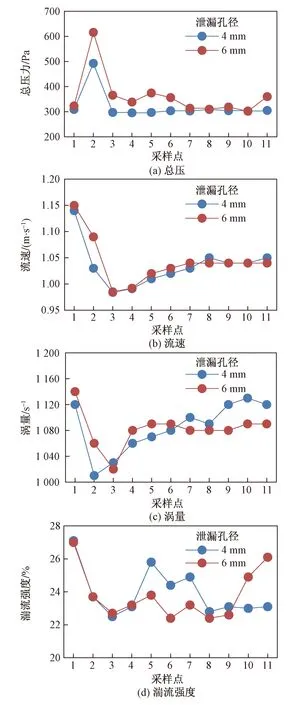
图9 波浪流泄漏模拟过程每0.01 s各参数变化曲线Fig.9 Simulates the variation curve of each parameter every 0.01 s in the leakage process of wave flow

由图9(a)发现，波浪流与分层流总压变化规律相同，球阀转动开始瞬间即第2个采样点处，管道内的总压最大，即此时管道内外压差最大产生瞬时泄漏声波幅值最大。前文理论分析得知波浪流的管道流动背景较大，这种泄漏声波信号与分层流相比容易被淹没在管道的流动背景噪声中。

由图9(b)发现，球阀在开启瞬间，最大流体流速曲线在球阀转动第0.01 s处流速大大减小，在第0.02 s到达最小值。球阀均随着开启时间延长，气液流速逐渐增大但是增大趋势变缓。产生这一现象的原因：管道内流体波浪流动特性，气液相界面为高速流动的气体携带液体向前波动。球阀开启，气体迅速扩散出管道，管道内气体流速大大减小。随着球阀继续开启，支管内气量越来越多，流速越来越大，同时主管道内的总流速降低。

由图9(c)发现，球阀真正开启时刻、涡量幅值急剧减小。波浪流稳定流动具有气液间相互作用大、涡量大的特点。球阀瞬间开启造成管道内气体流速减低，减小了气液两相间的相互作用，从而管道内流动背景噪声减小。整个球阀转动过程造成分支管道内涡量增加，相对于其开启大大减缓主管道内的涡量相比作用仍较小。

由图9(d)发现，整个球阀开启过程湍流强度变化呈现波浪式变化。因为波浪流管道内稳定流动时，湍流变化同样呈现波浪式变化，球阀开启在一定程度上减缓了主管道内的流体湍流强度，分支管道内的湍流强度变化与主管道变化相比很小。

总体上说，波浪流发生泄漏，球阀开启瞬间，管道内外压差最大，产生泄漏瞬时声波信号幅值最大。球阀在真正开启时刻附近造成气液流速大大降低且管道内涡量急剧减少，一定程度上减缓了管道内的湍流强度。说明上部泄漏大大削弱管道内的流动噪声信号。因此波浪流发生上部泄漏时，可通过分析泄漏发生后管道内的流动噪声的明显减小来进行分析判断。

5.3 段塞流泄漏开启模拟参数分析

同理，分析段塞流泄漏流场，各参数最大值的变化如图10所示。分析发现，主要有以下结论。

图10 段塞流泄漏模拟过程每0.01 s各参数变化曲线Fig.10 Simulates the variation curve of each parameter every 0.01 s in the leakage process of slug flow

(1)球阀在开启过程，管道内总压波动性不断加强，且泄漏孔径越大波动性越强。流速在开启过程中出现最大峰值，流速变化具有波动性。湍流强度在泄漏过程呈先减小后增加趋势，但是球阀未开启与完成球阀开启后的差值不大。

(2)涡量在球阀球芯开启过程中变化不明显，在球阀完全开启后涡量增加，远大于未开启动状态，说明此时管道内产生的泄漏声源最大。结合文中段塞流泄漏流动特征以及泄漏持续声源发生的时间分析得知，涡量可能是段塞流泄漏持续声源的重要组成部分。通过分析管道泄漏发生前后涡量变化可实现泄漏判断。

5.4 不同流型泄漏开启过程模拟对比

对分层流、波浪流和段塞流不同工况下，泄漏开启过程中各参数即气液流体的压力、流速、湍流强度和涡量最大值变化进行分析对比，得到不同流型泄漏流场的泄漏开启时各参数特征如下。

5.4.1 分层流

球阀开启瞬间，管道内压力最大、流速最小，内外压差最大，产生泄漏声波信号最大幅值。开启附近的涡量和湍流强度最大，泄漏声源主要由偶极子和四极子声源组成。

5.4.2 波浪流

球阀开启瞬间，管道内压力最大、流速最小，内外压差最大，产生泄漏瞬时声波信号，涡量最小，湍动强度呈减小趋势。涡量和湍流强度均减小可知流动噪声减小，泄漏前后流动噪声变化可以进行泄漏判断。

5.4.3 段塞流

球阀开启过程，管道内总压波动性不断加强，且出现流速最大值；球阀完全开启时涡量最大。泄漏发生前后涡量变化可以进行上部泄漏判断。

由表3知，分层流通过泄漏发生时的瞬时泄漏声波信号就可以很好地进行泄漏判断。而波浪流和段塞流的泄漏判断必须依赖于对瞬时泄漏声波信号和泄漏后管道内流体流动状态，要得到较为准确的泄漏判断，需要综合分析这两种信号的泄漏特性，这与前期获取的实验数据分析相一致。

6 结论

采用简化的几何模型，基于Fluent动网格技术通过UDF编程实现气液两相流管道泄漏开启过程和完成的流场模拟，从泄漏流场各参数变化分析泄漏声源特性与理论相验证，是为了补充前期的实验在采集流动参数方面的不足，主要得到如下结论。

(1)分层流在球阀真正开启的瞬间，管道内总压、涡量、湍流强度均为最大值，流速为最小值。泄漏声波信号主要产生于球阀开启瞬间，瞬时声源能够很好地进行泄漏判断。

(2)波浪流球阀开启瞬间，管道内总压、涡量均为最大值，流速、湍流强度均为最小值。上部泄漏后的管道内压力和流速较稳定。

(3)段塞流在球阀开启过程，总压、气液流速和湍流强度变化规律性不强；开启过程会出现流速最大值；球阀完全开启时涡量最大。需要主要靠泄漏完成流场参数变化来进行判断。通过分析泄漏后流场参数变化发现，上部泄漏主要造成泄漏孔后主干道内流体流动趋于流动状态不断变化。

需要注意的是，为了弥补声波泄漏检测实验过程中无法测量的参数问题而进行该理论研究，不可代替实验。