PDMS基光子器件的耦合光栅与波导研究

刘启发，张 琳，赵子岳，胡金高娃，宾璟橦，成谢锋

1.南京邮电大学通信与信息工程学院，江苏 南京 210003

2.南京邮电大学电子与光学工程、微电子学院，江苏 南京 210023

近年来，柔性材料以可拉伸、可折叠、可弯曲等性质在光子器件领域拓展出特有的光电性能，同时柔性光子器件具有低能耗、抗电磁干扰等明显优势［1］，因此在通信技术［2］、传感技术、生物医学等多学科交叉领域具有广阔的应用前景。

聚二甲基硅氧烷（PDMS）以其优异的化学惰性、热稳定性、光学透明性和生物相容性在医疗卫生［3－7］、光互连［8－11］、生物表皮传感［12－13］等领域被广泛应用。2015年，Karrock等［3］提出通过调控PDMS布拉格光栅的眼部压力传感器，用于治疗青光眼和增强人工晶状体；与之类似，通过布拉格光栅的滤波波长⁃光栅参数⁃受力的关系实现力敏检测的PDMS光学力敏传感器应用于表皮传感［6］；以及在光互连领域拉伸和弯曲波导不会大程度增加额外损耗的PDMS 可拉伸光波导链路［10］。

由于PDMS材料成本低廉、适用领域广泛以及微纳米加工技术的发展，2012年，Ramuz等［6］设计了两个厚度为600 μm的PDMS双向集成型波导耦合光栅压力传感器。2021年，Peng等［13］提出类似结构并通过硅光栅模板获得PDMS耦合光栅，因其基于布拉格条件可以很好地实现光子信息的高效获取，并且具有较高的空间自由度、较小的对准容差，有利于光子芯片的集成封装［14］。在PDMS基集成光子器件的研究［11，15－18］中，Bosman 等［10］提出应用于通信网络WDM的集成光学器件：存在单个波导光栅的非对称型PDMS布拉格耦合器（ABC）的滤波器；在传感系统中的PDMS材料是芯片实验室（LOC） 技 术 的 绝 佳 材 料。 Jandura 等［16－17］基 于PDMS与当前制造技术的兼容性，提出通过将DLW工艺与PDMS压印工艺相结合来制造PDMS各种波导结构，并且设计使用多种技术制造类型多样的PDMS基光子器件以用于芯片实验室技术。

虽然PDMS基光子器件有一定的研究报道，但波导光子的高效获取和低损耗传输仍然是制约其走向应用的问题之一，尤其是缺乏针对低损耗单模波导集成的光栅耦合研究。针对于此，并基于光栅耦合和单模波导在光子器件中的基础地位，本文进行面向紫外和可见光波段的PDMS薄膜单模波导和耦合光栅的基础性研究，通过解析计算和有限元（FEM）仿真，优化设计波导和光栅结构，进而实现高效率光子获取和低损耗波导传输，为PDMS基光子器件奠定理论和应用基础。

1 PDMS单模波导设计

设计PDMS薄膜平面光子器件结构的目标是实现高效光波的耦合获取，同时避免不同波导模式引起信号失真和模式之间的能量转换问题，以实现低损耗芯片光子传输。为此，首先设计对称型PDMS基模波导结构（无衬底，波导上下包覆层为空气），这类光波导用于光波传输时基模永不截止［19－22］，并根据几何光学相关公式推演出在特定的波长下的单模传输条件：光波导厚度与波长的约束关系，如式（1）［21］所示。

式中，n1和n2分别为PDMS和空气的折射率，d为波导的厚度，λ为光波长，选取PDMS透明波段300～800 nm的中心波长550 nm，PDMS材料在此波长下的折射率为 1.4［18，23－24］，空气包层的折射率为 1。

图1 单模条件下入射光波长与波导厚度的关系

2 耦合光栅仿真设计

研究设计耦合光栅意在实现平面波导光子的获取，当光波以入射角θi入射到光栅周期性结构时，导波模式中每一个基本传播模式的波长都会受到周期性的调制形成一系列的空间谐波，空间谐波在光波导中传输时，经过一个光栅周期后，相位和下一个光栅周期相同或者相差2π的整数倍时，由于相位匹配相干叠加实现外部光波的耦合［19－22，25］。 其相位匹配的布拉格条件如式（2）［20］所示。

式中，T表示光栅周期，Neff表示光栅区的有效折射率，n1为PDMS材料折射率，q为光栅衍射光的级数。研究使用1级衍射波矢匹配波导中0阶导模传输（即q＝1），从而确定研究理想状态下的光栅耦合方程。

使用基于FEM的COMSOL Multiphysics软件对光栅进行二维仿真，图2（a）所示为PDMS耦合光栅FEM二维仿真模型图，微纳光栅作为波导光子的输入耦合器，其三维结构示意图如图2（b）所示，对于薄膜波导最好的方式是采用脊型波导结构，另外所设计的波导端楔形结构可以更进一步地减少光栅和波导间耦合的光损耗［26］。其中光栅周期T，光栅齿宽a，波导厚度d以及占空比dc＝a/T是其主要结构参数。本研究将占空比dc设置为0.5，波导厚度d设置为280 nm，使用横电模（TE）偏振光以θi＝10°的角度入射以打破衍射对称性，使得光栅耦合的二阶布拉格反射引起的背向反射最小［18－21］，进而提高耦合效率。

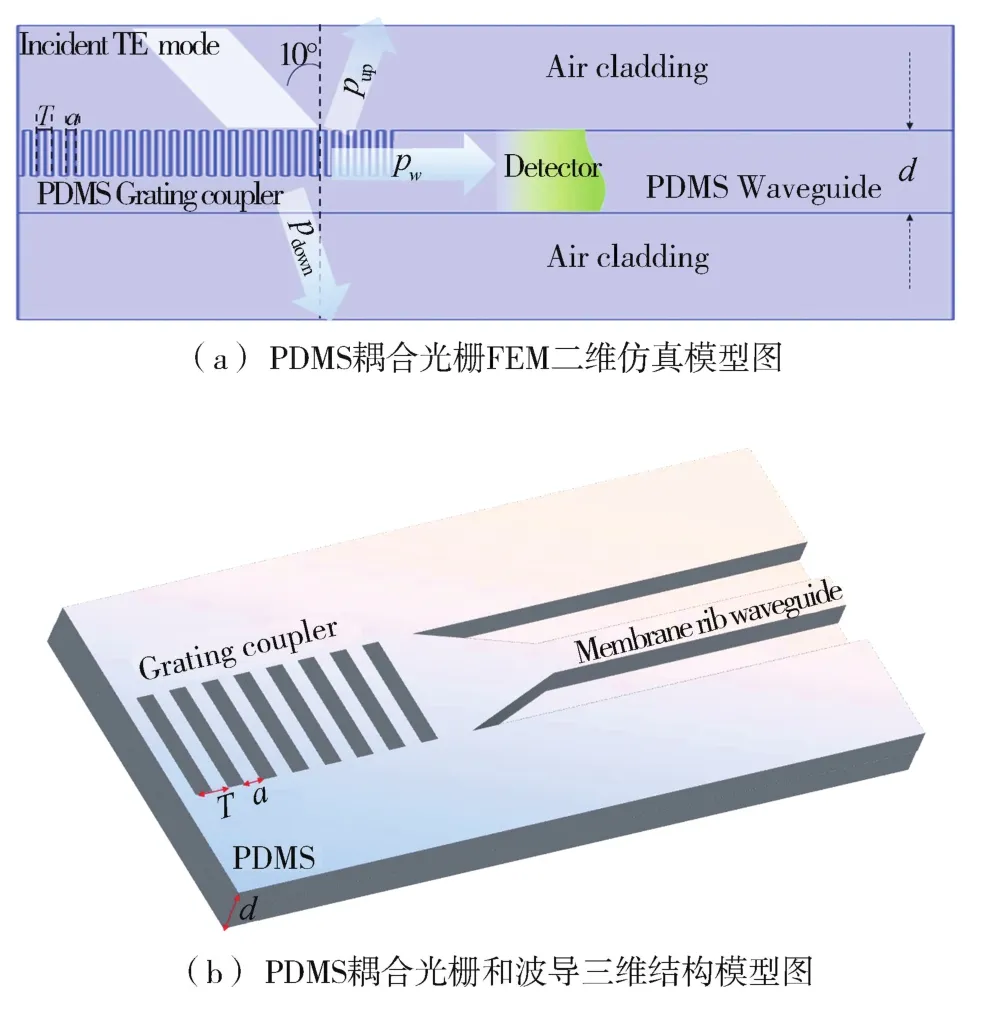
图2 PDMS耦合光栅示意图

光栅耦合效率η的计算公式如式（3）所示。

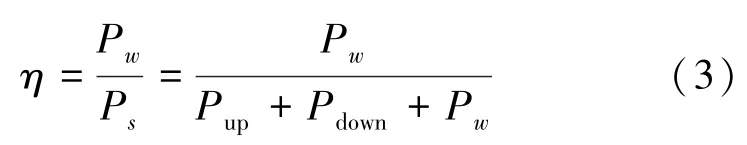
式中，Ps为入射光功率，Pw为耦合进入光波导中的光功率，Pup为辐射进入顶部空气包层的光功率，Pdown为辐射进入底部空气包层的光功率。

除已固定的参数外，光栅刻蚀比和光栅周期对耦合效率有不同程度的影响，需要在设计过程中进行精确优化。对0.1～1的刻蚀比以0.05的步长仿真其对耦合效率的影响；对300～800 nm的光栅周期范围，以10 nm的步长仿真其对耦合效率的影响。图3（a）所示为光栅刻蚀比和光栅周期对耦合效率的综合影响结果。基于550 nm的入射光波长，其耦合带中的光栅周期范围在500～600 nm之间，刻蚀比在0.55～0.95之间。光栅周期在540～570 nm的范围时，光子耦合效率较高，最高可达22.3%。此结果与本文解析计算的结果趋于一致，具体讨论如下：根据布拉格条件式（2），其中TE模下光栅区的有效折射率Neff通过式（4）计算，其中的Neff1和Neff2由式（5）计算。

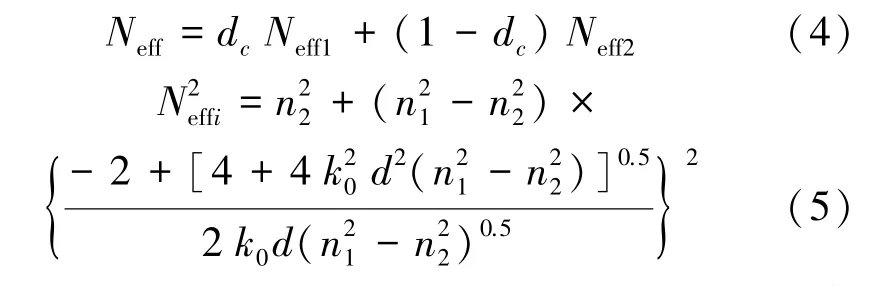
式中，Neff1和Neff2分别为未刻蚀处波导的有效折射率和刻蚀处波导的有效折射率。

由计算得，未刻蚀处波导的有效折射率为Neff1为1.23，Neff2和Neff的计算结果以及根据布拉格条件计算出的周期见表1，光栅刻蚀比从0.55增长到0.95的过程中，光栅区有效折射率Neff逐渐减小，因为满足相位匹配的光栅周期与光栅区有效折射率Neff成反比，因此在表1和图3（a）中均明显地体现出耦合带中的光栅周期在0.55～0.95的刻蚀比下呈现增长趋势。表1中所计算出的周期值与图3（a）FEM仿真优化出的结果实现了大致的吻合，但是由于有效折射率的计算误差和仿真步长的精确程度影响，故理论值与仿真数据只能近似比拟。

表1 基于布拉格条件的光栅参数解析计算结果

图3（b）所示为刻蚀比为0.9，光栅周期为570 nm时，以300～800 nm的光波段入射到光栅结构，光波在550 nm左右达到最高耦合，显示峰值损耗约为6 dB；图3（c）所示为刻蚀比 0.6，光栅周期为550 nm时，光波在560 nm附近达到最高耦合，显示峰值损耗约为7 dB。图3（d）（e）中是波导的共振模式与周期性F⁃P微腔阵列的光子结构共振模式之间的耦合效应，即每个光栅条在光传播方向上充当F⁃P谐振腔，可以通过改变光栅参数使得谐振模式与波导模式发生高效耦合［19－22，25］，与 此 同 时，图3（b）（c）中面向550 nm绿色可见光波具有较小的光学展宽。可以通过选择性调控光栅的周期，达到对入射光的波长选择性获取，使得基于PDMS波导的光栅耦合器件在灵活性和可控性上达到平衡。

图3 有限元法数据仿真结果图

3 结束语

基于柔性光子技术广阔的应用空间和PDMS的弹性、化学惰性、热稳定性、透明性和低成本等优异性能，对面向紫外和可见光波段的PDMS薄膜波导和耦合光栅进行了基础研究。通过解析计算和有限元仿真，优化设计波导和光栅结构。研究表明，在基于单模波导传输的条件下，刻蚀比为0.9，光栅周期为570 nm下可以实现PDMS透明波段的中心波长550 nm的6 dB优化耦合损耗。对于包括紫外波段的其他PDMS透明波段，均可采用本研究的方法优化出针对特定波段的高效耦合光栅和波导参数。这项研究工作为面向紫外光和可见光波段的PDMS基光子器件的发展和应用开拓道路并提供基础。