小议向量背景下高考立体几何大题载体模型建系

凡森泉

摘要：以近些年高考改革的实际现状作为切入点，综合中学向量以及立体几何这两种教学体系之间的联系进行分析。建立在高考试题的基础上，针对几何图形进行归类，总结具体的空间直角坐标系的建立方法，确保能够为相关教学体系改革以及研究提供参考依据。

关键词：向量;立体几何;载体模型

一、基础分析背景

综合空间向量的知识体系来讲，空间向量本身具有一定的代数形式和几何形式，这种双重性进一步增加了空间向量在多种知识点中的应用价值。它建立在数形结合的基础上，打造了新的数学解题和思考工具，能够以结合已知条件构建坐标系，通过向量本身的性质以及运算逻辑，提供更为明确且简单的证明方法[1]。因此空间向量在融入了数学教材之后，在解决立体几何位置关系以及其他问题时有一定的促进作用，并且这种解题方式也写入了高考中。

综合实际的应用情况来看，空间向量在立体几何解题过程中，常用的方式以几何推理和向量解法为主，而近些年的高考中也存在大量的典型习题，能够为后续空间直角坐标系的建立方法提供清晰明确的指引。

二、基础原理简述

建立空间直角坐标系的核心依据便是实现空间向量基本定理与空间图形的融合。我们假设存在这样一组不共面：，那么针对任意一个空间向量都存在着唯一的一对有序实数组（x，y，z），促使。

而综合具体的逻辑分析来看，如果将其中三个基向量转化成可以两两相互垂直的三个单位向量，那么既有的有序实数组（x，y，z）就可以称之为向量在空间直角坐标系中的具体坐标，这一理论在当前的诸多习题中，我们都可以以这种逻辑思维方式进行思考，这样能够有效解决部分复杂的几何问题。

三、基于高考题型的空间向量建系逻辑

（一）常见的规则几何体和建系逻辑

常见的规则几何体主要以正方体、长方体以及各类型棱柱为主，在当前的高考中频繁出现，并且成为了最基础的几何图形解题类型，以下选择长方体作为主要的题型进行代表性分析。

（1）正四棱柱

从实际的建系角度来讲，可以利用同一顶点处的三条棱两两相互垂直的原理进行思考，另外边长相等以及倍数关系也可以作为建系的主要参考依据[2]。

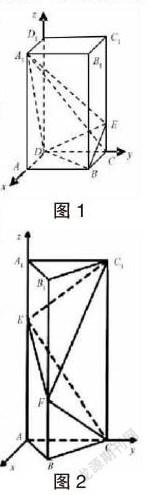
例题1：存在一个正四棱柱ABCD—A1B1C1D1，其中AA1=2AB=4，点E在CC1上，并且C1E=3EC。见图1。求證：A1C垂直平面bEd（垂直吗？），求二面角A1-DE-B的大小。

（2）三棱柱相关习题

从解题角度分析，可以直接建立在直棱柱侧棱与底面面垂直关系以及底面三角形中的线的垂直特性角度进行计算。

例题2：在2011年的湖北卷高考习题中，已知正三棱柱ABC-A1B1C1的底面边长均为2，则侧棱的长度为，侧棱AA1上有一点E，BB1上有一点F，且AE=，BF=。如图2。求证CF垂直于C1E，求二面角E-CF-C1的大小。

（二）不规则几何体及其建系规则

结合不规则几何体的实际情况来看，与规则几何体之间的主要差异便是需要学生具备较强的空间逻辑思维，能够将平面上的习题已知条件转化为立体空间中的关系，这样才能够实现知识逻辑关系的定位。

（1）折叠问题

首先，针对折叠问题进行分析，其中边和角存在变与不变的特点，定位这些特殊的关系，最后能够得出较为明显的相互垂直的线[3]，这样可以实现快速的建系。

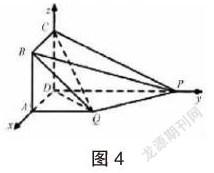
例题4：在梯形ABCd中上下底边分别为2和6，高为，沿着对称轴OO1进行折叠，折成直二面角。如图4所示。求证AC垂直于BO1，求二面角O-AC-O1的大小。

（2）非规则几何体的实际分析以及建系

首先从空间向量的角度进行分析，若图中未能提供具有已知条件的两两相互垂直的直线，那么首先应该找到一个线面的垂直关系，然后在这个垂直关系中找到经过垂足的两条相互垂直的直线，同时还要考虑到合理建系的实际规则，即促使相关点的坐标可以在整个坐标中凸显出来，且形式较为简单，这样能够有效减少计算量。

例题5：已知ABCD为正方形，其中PD垂直于平面ABCD，且PD平行于QA，QA=AB=1/2PD。如图5所示。求证，PQC垂直于平面DCQ，同时求二面角Q-B-PC的余弦值。

结束语：

结合近几年的新课程高考考题来看，几何问题的解析可以直接通过向量问题来进行优化，其中不仅可以简化思考逻辑，也能够进一步实现多种知识点之间的相互转换，对于强化学生的综合能力有一定的促进作用，同时也可以为未来的课程优化以及教学体系创新提供有效的参考依据。

参考文献：

[1]齐鹏飞.借力空间向量法巧解立体几何轨迹问题[J].理科考试研究，2021，28（21）：13-16.

[2]董军浪.几何点及其坐标/向量的规范表达[J].西安工业大学学报，2021，41（05）：514.

[3]王春芳.例谈立体几何四面体中关于“棱”的问题[J].中学生理科应试，2021（10）：13-15.