基于Poynting矢量行波分离的最小二乘逆时偏移
王晓毅, 张江杰, 许宏桥, 田宝卿
1 中国科学院地质与地球物理研究所, 中国科学院油气资源研究重点实验室, 北京 100029 2 中国科学院地球科学研究院, 北京 100029 3 中国科学院大学, 北京 100049 4 中国科学院地质与地球物理研究所, 中国科学院页岩气与地质工程重点实验室, 北京 100029
0 引言
作为一种基于双程波动方程进行波场延拓的成像方法,逆时偏移具有诸多优点:可以利用反射波、多次波、回转波和棱柱波等各种波型,不受地层倾角的限制,并且对起伏地表和复杂速度分布有很好的适应性.但是相较于单程波偏移算子,逆时偏移面临着由背向反射所引起的低频噪声发育的问题.所谓背向反射,是指在震源波场或者检波器波场延拓过程中,当波遇到波阻抗界面时所发生的次生反射.背向反射波与正常传播的波之间的互相关在地震剖面上所表现出的结果即低频噪声(刘红伟等,2010;杜启振等,2013).一般而言,界面波阻抗差异越大,背向反射越发育,低频噪声越强.
常规的偏移方法受低覆盖的观测系统,波的几何扩散、吸收衰减等效应引起的弱振幅,有限偏移孔径造成的低分辨率,以及震源子波的震荡等诸多因素的影响,串扰噪声和偏移假象比较发育(Schuster,2017).相比之下,最小二乘偏移(LSM)通过观测数据和理论数据的不断拟合和校正,取得的成像结果振幅保真性好,分辨率和信噪比更高(马方正等,2016;李振春等,2017).最初,LSM主要用于射线类和单程波类偏移算法,效果显著.后来,最小二乘逆时偏移将最小二乘思想和逆时偏移方法结合,既可以利用各种波携带的信息,又可以得到能量更加均衡且消除了采集脚印的地下结构剖面.
在逆时偏移(RTM)中,关于低频噪声的压制有着诸多办法,例如Laplace滤波、成像角度限制等(Zhang et al., 2007; Yoon and Marfurt, 2006).相应地,这些技术也被引入LSRTM中,并取得了良好的效果(杨凯和张剑锋, 2017; Yang and Zhang, 2018).以Laplace滤波为例,我们可以在每次迭代求取梯度之后对其进行滤波消除噪声,但是这改变了振幅和相位信息,因此需要预先对震源子波进行二次积分并对求取的梯度进行振幅补偿.近些年来,一种基于行波分离的成像方法被提出(Liu et al., 2011; Fei et al., 2015).根据入射波和出射波之间的几何关系,我们可以发现两者是分别沿着下行和上行方向的.Liu等(2011)提出只保留震源波场和检波器波场沿不同垂直方向的组分之间的互相关作为新的成像条件,从而有效地压制地震剖面中的低频噪音.Fei等(2015)进一步提出只保留震源波场的下行波和检波器波场的上行波之间的互相关运算,以避免回转波产生的偏移假象.王一博等(2016)分别将震源波场和检波器波场分离为左上、左下、右上和右下四个组分,并将震源波场和检波器波场的这些组分两两互相关运算,得到了16种成像结果,有效地分析和分离了低频噪声和串扰噪声.值得注意的是,以上的波场分离主要是在波数域实现的,涉及到Hilbert变换和Fourier变换,因而计算量较大,存储成本较高.
Poynting矢量提供了波场传播的方向信息,因此无论是在声波还是弹性波地震成像都有着广泛而充分的应用.一方面,Poynting矢量被用于压制低频噪声(Yoon and Marfurt, 2006);借助震源波场和检波器波场的方向信息,我们可以得到入射波与出射波之间的张角,并在成像条件中添加张角(或者入射角)加权项对大角度进行衰减或截断,以达到压制噪声的目的.另一方面,Poynting矢量还可以被用于提取角度域共成像点道集(ADCIG),包括张角道集和倾角道集(王保利等,2013; Liu and Zhang, 2018).这些道集为AVA、MVA等分析提供了依据.在本文中,借助Poynting矢量所包含的方向信息,我们以较低的代价获取波场的上行波组分和下行波组分(黄杰等,2018).特别是为了使Poynting矢量求取的鲁棒性更强,我们采用了一种局部最小二乘意义下的求取结果(芦永明等,2017).
本文结构如下:首先,我们回顾了LSRTM的基本原理,对Born近似和迭代反演进行了阐述.其次,通过对双程波动方程类偏移方法成像条件的分析,解释了低频噪声的产生和压制方法,并提出了对LSRTM梯度算子的改造.然后,我们引入Poynting矢量并利用其方向指示性实现了行波分离,提高了算法实现的效率.最后,通过数值算例验证了我们方法的有效性.
1 基本理论
最小二乘逆时偏移通过迭代反演得到的最终剖面具有更高的分辨率.为取得更快的收敛速率,我们通过在梯度构建中对震源和检波器波场分别选择合适的组分进行互相关运算以压制低频噪声和偏移假象.特别地,Poynting矢量的引入使得我们方案的实现变得方便快捷.
1.1 最小二乘逆时偏移
按照扰动理论,真实速度v可以分为偏移速度v0和扰动速度δv两部分,对应的波场分别为背景波场p0和扰动波场δp.根据Born近似,扰动波场由背景波场和速度扰动共同决定,即:
(1)
其中,xs表示震源所在的位置,x是任一空间坐标点,t表示时间,f是震源子波.m(x)=2δv(x)/v0(x)表示扰动模型,也叫真实反射率,刻画了偏移速度与真实速度之间的偏离程度.在检波器位置xr上记录扰动波场,我们可以得到模拟数据d,即:
d(t,xr)=δp(xr,t;xs).
(2)
由以上叙述可知,借助于Born近似,我们可以建立扰动模型与观测记录之间的线性关系.以矩阵的形式对此加以表达,我们有:
d=Lm,
(3)
在这里,L为正演算子,也被称为反偏移算子.
在已有观测系统和采集记录dobs的情况下,求取扰动模型m需要用到正演算子的逆L-1.然而,对于地震勘探而言,遇到的反问题本身就是病态的,L-1往往并不存在.另一方面勘探范围大,处理的数据也是海量的,因此直接求逆从运算量和存储量上也不可行.所谓最小二乘方法,就是通过迭代的方法来逼近反问题的最优解,从而避免直接的取逆.目标函数选用预测数据d与观测数据dobs之间残差的L2范数,残差反传使得模型不断被校正,直至预测数据和观测数据足够接近.在成像过程中,梯度算子LT也被称为偏移算子,按照伴随状态法可以表示成如下形式(Plessix, 2006):
(4)
其中,q是伴随波场,满足:
(5)
对于常规的逆时偏移,通过一次震源波场正向延拓和检波器波场反向延拓且以(4)式为成像条件可以得到地下结构的成像剖面mmig.在最小二乘逆时偏移中,以(4)式作为梯度对反演结果不断进行校正,可以消除成像剖面中由采集脚印和非均匀照明引起的偏移假象.相较于常规偏移,最小二乘偏移的运算量需求更加庞大.在每次迭代过程中,仅梯度计算就需要一次震源波场(包括背景波场和扰动波场)正向延拓和检波器(伴随)波场反向延拓.在这里需要指出的是,我们每次迭代更新的是反射率模型m,而非速度模型v.
求解最小二乘问题的最优解涉及到的迭代方法包括最速下降法(SD),共轭梯度法(CG)以及拟牛顿法(QN)等.在本文中我们采用带有预条件的共轭梯度算法来对反问题进行求解.这一方法的优点在于其既避免了对Hessian阵显式求逆,又克服了最速下降法收敛慢的缺点,并且所需存储量少,稳定性高(Schuster, 2017).
1.2 低频噪声的产生与去除
波动方程是数值模拟地震波传播过程的理论依据,一方面它可以生成包括一次反射波和多次波在内的多种类型的波,另一方面它具有同时刻画波沿各个方向传播的能力.因此,相较于一般的单程波偏移算法,逆时偏移具有如下优势:处理回转波、棱柱波等特殊波型十分方便,不受地层倾角限制且具有更大的照明区域.然而,强振幅的低频噪声往往会污染偏移结果,特别是在浅层和强反射界面的上部.当背向反射发育时,对震源波场和检波器波场采用传统的互相关条件会沿着射线路径成像,从而在偏移剖面上产生强烈的干扰.
对于双程波偏移方法,基于全波的互相关成像条件可以写为
(6)
其中,us和ur分别表示震源波场和检波器波场,上标u和d则分别表示上行波场和下行波场.由式(6)可知,除了震源波场的下行波和检波器波场的上行波可以成像外,其他组分也参与成像.其中,沿相同方向传播的组分互相关运算会产生较大幅值的噪声,这种噪声在频率域表现出低频特征(杜启振等, 2013),因此可以用Laplace滤波加以消除.但这也会改变地震剖面同相轴的振幅和相位特征,因此需要对震源的预处理和额外的矫正.为了提高成像质量,可以改造成像条件,即省略(6)式的后两项来压制低频噪声.从而,我们得到了新的成像条件(Liu et al., 2011):
(7)
对于一次反射或者散射,震源波场的入射波下行而检波器波场的出射波上行,如图1a中的A点和B点所示.特别地,对于多次波的一些反射点也满足这一特征,如图1b中的C点.式(7)中右侧的第一项可以很好地将这部分波加以利用,使其在正确位置成像.对于如图1b中的D点,式(7)中右侧第二项满足对其成像的要求.但是当偏移速度变化特别剧烈时,回转波会在剖面上产生假的同相轴(Fei et al.,2015),如图2所示.这会对后续的处理和解释造成困扰.因此,式(7)又可近一步简化为
(8)
最小二乘逆时偏移与常规的逆时偏移一样,都面临着双程波成像所带来的低频噪声和串扰噪声问题.因此,我们可以仿照上述成像条件对梯度算子进行改造.与式(7)和(8)相对应,我们分别有:
(9)
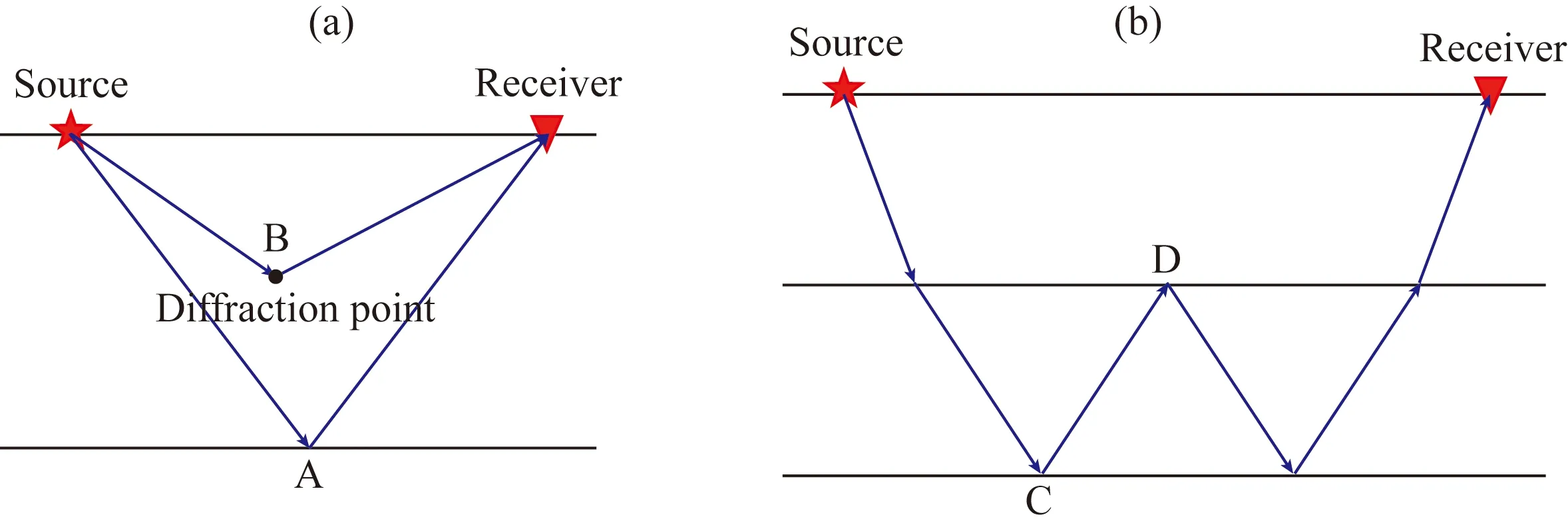
图1 波的传播路径(a) 反射波和绕射波的传播;其中A点为反射点,B点为绕射点; (b) 多次波的传播路径.C点和D点均为多次反射点,但是适用于不同的成像条件.Fig.1 Wave propagation paths(a) Propagation of reflected and diffracted waves. Point A is the reflection point and point B is the diffraction point; (b) The propagation path of multiples. Points C and D are multiple reflection points, but they are suitable for different imaging conditions.
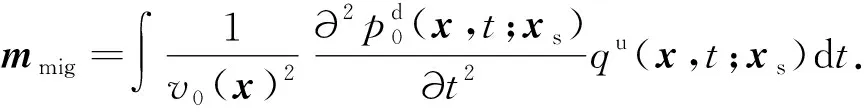
(10)
1.3 Poynting矢量与上下行波分离
从物理意义上来说,Poynting矢量是方向性的能流密度矢量,其大小为单位时间穿过单位面积的能量.这一矢量在电磁勘探和地震勘探领域有着重要的意义和作用,特别是其良好的方向指示性对波传播的刻画和反演成像有着很大的帮助(王保利等,2013).
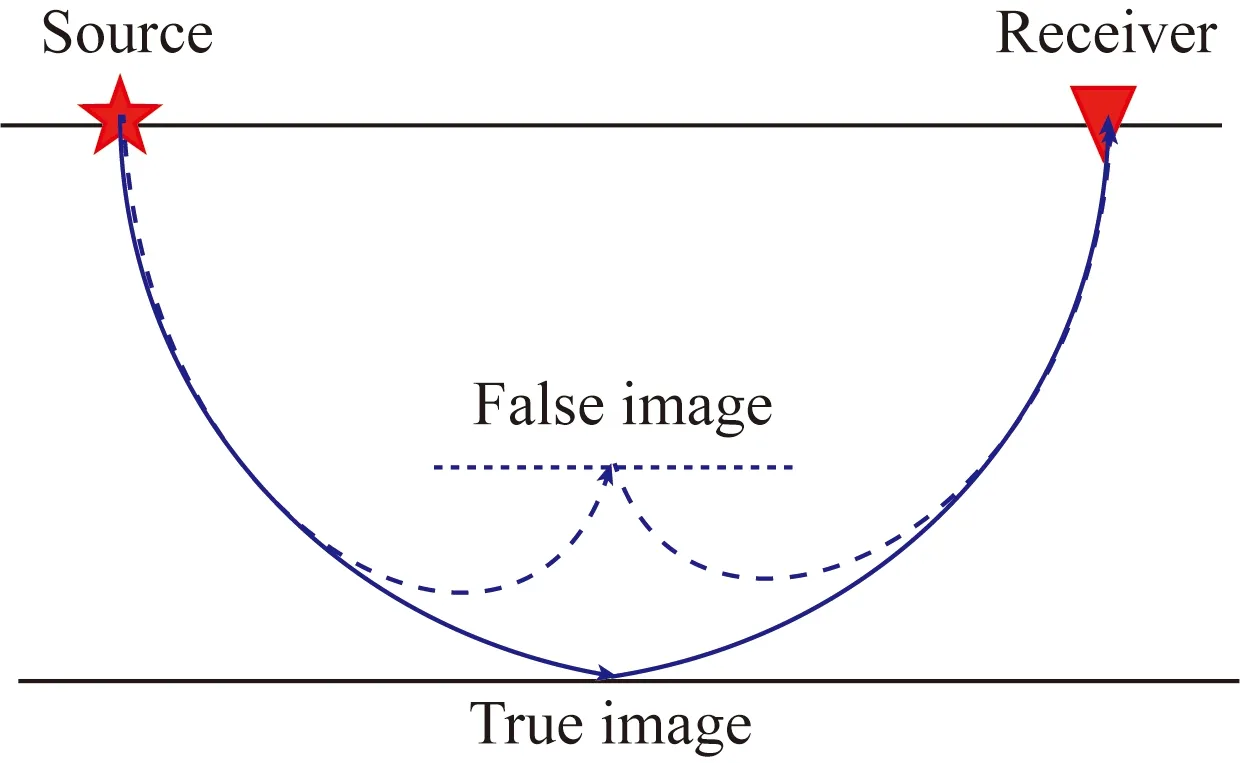
图2 偏移假象产生示意图当偏移速度存在剧烈变化区域时,能够在正确的位置成像,而则会生成虚假的轴.Fig.2 Schematic of the generation of migration artifactsWhen there is a sharp change in the migration velocity, energy is generated in the correct position by using but the false image is also produced by
对于声波介质,Poynting矢量可以按照式(11)进行计算(Yoon and Marfurt, 2006):
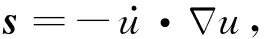
(11)

基于(11)式的Poynting矢量求取面临计算的稳定性问题,也就是当声压场达到峰值时,s的幅值为0,从而丧失了其方向性.为使算法更加稳健,局部最小二乘平均意义下的Poynting矢量被提出(芦永明等,2017),即:
(12)
其中,i表示代求点,Ω表示i点的邻域.
图3a是声波在速度为1000 m·s-1的均匀模型中传播的波场快照,其传播时间为0.2 s.红色箭头即为按照(11)式和(12)式所求的Poynting矢量,其指向声波的传播方向,也就是波前面的外法线方向.按照Poynting矢量的指向,我们可以非常方便快捷地完成波场的上下行波分离.如图3b、c所示,波场被分为上下行波两部分.对于复杂波场我们也可以按照这种方式对波场进行分离.图4a是一复杂模型,将震源置于模型中间位置激发,在传播时间为0.6 s记录下的波场快照如图4b所示.与此同时,我们求取了Poynting矢量,并在图4c、d中分别展示其x分量和z分量.按照Poynting矢量的指向,我们对复杂的波场快照进行了分离(图4e、f).值得注意的是,对于波场重叠的区域,(11)式只能给出单一方向,这意味着这种简单的分离对于重叠区域是存在误差的.当偏移速度足够光滑时,波的混叠并不严重,因而对成像造成的影响并不大.
1.4 方法流程
尽管通过改造梯度算子,可以避免低频噪声和假象的产生,但是这也有可能会造成部分有效信号的丢失.特别地,Poynting矢量在重叠区域只能给出一个方向,导致部分能量被错误地归位.为了降低这部分的影响,我们将改造后的梯度算子只用在早期的迭代中,并根据迭代次数或者数据误差的阈值在后边调整回全波的梯度算子,从而充分利用所有波所携带的地下信息.
结合上述理论,我们将LSRTM的整体工作流程总结如下:
(1)根据偏移速度v0正演得到模拟数据d0,并让原始数据dobs减去其得到dres;
(2)设定初始反射率模型m0,并基于Born近似计算模拟数据Lm0,从而得到残差r=Lm0-dres;
(3)利用偏移算子(9)或者(10),将残差反传得到gk+1=LTr;
(4)根据带有预条件的共轭梯度法,利用gk、gk+1和zk分别计算模型更新方向zk+1和迭代步长α,即:
(13)
其中,P算子表示震源照明补偿.随后,完成模型迭代mk+1=mk-αzk+1;
(5)计算数据残差r=Lmk+1-dres,重复第3步和第4步,直至‖r‖2小于某个阈值或者迭代次数达到预定次数;
(6)利用偏移算子(4),将残差反传得到gk+1=LTr,重复第4步,直至误差低于某个阈值或者迭代次数达到设定值.

图3 均匀介质中声波Poynting矢量的求取及上下行波分离(a) 0.2 s时刻的波场快照;红色箭头表示归一化后的Poynting矢量,沿波的外法线方向; (b) 上行波场; (c) 下行波场.Fig.3 Calculation of Poynting vector for acoustic waves and the up/down wavefield decomposition in the homogeneous medium(a) Snapshot of acoustic wave at 0.2 s. The red arrow represents the normalized Poynting vector, which is along the outer normal direction of the wave; (b) Upgoing wavefield; (c) Downgoing wavefield.

图4 复杂介质中声波Poynting矢量的求取及上下行波分离(a) 复杂介质速度模型; (b) 0.6 s时刻的波场快照; (c) Poynting矢量的x分量; (d) Poynting矢量的z分量; (e) 上行波场; (f) 下行波场.对于波场发生重叠的区域,Poynting矢量只能给出一个方向.Fig.4 Calculation of Poynting vector for acoustic waves and the up/down wavefield decomposition in a complex medium(a) Velocity of the complex model; (b) Snapshot of acoustic wave at 0.6 s; (c) x-component of the Poynting vector; (d) z-component of the Poynting vector; (e) Upgoing wavefield; (f) Downgoing wavefield. The Poynting vector gives only one direction for the overlapping area of the wavefield.
2 数值算例
为了解释方法的有效性,我们用两个数值算例进行了验证.其中既包括简单的双层模型,又包括相对复杂的Marmousi模型.偏移所需要的地震记录数据集由时间二阶,空间八阶的有限差分算法模拟得到.
2.1 双层介质
模型界面位于500 m处,上层介质速度为1000 m·s-1,而下层介质速度为1500 m·s-1.震源子波设置为主频25 Hz的雷克子波,将其在地表激发且间隔设为250 m.所以,总炮数为5,从左至右依次排列.检波器置于地表,空间间隔5 m,时间采样间隔为0.5 ms,总记录时长为2 s.

偏移所用的速度模型是由真实模型经高斯光滑所得,并由此计算出真实的反射率模型.在进行LSRTM之前,我们选取第三炮的数据对正演算子和偏移算子进行了点积测试.表1详细列出了我们点积测试的结果,可见无论是采用公式(4)还是(9)或者(10)作为偏移算子,都近似满足〈Lm,Lm〉=〈m,LTLm〉以及〈LTLm,LTLm〉=〈Lm,LLTLm〉.
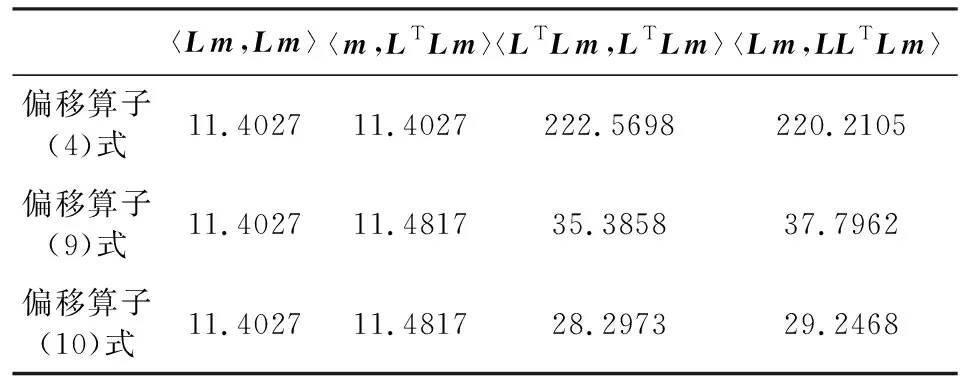
表1 双层介质点积测试结果Table 1 Dot product test result for a two-layer model
此外,因为公式(9)、(10)不能保证像公式(4)一样与正演算子满足充分的伴随关系,其测试结果的相等性要差于公式(4)测试结果的相等性.图6a、b、c分别是三种成像条件对应的偏移结果,可以看出相比于全波梯度算子(4),成像条件(9)和(10)产生的单炮剖面更为干净,没有低频噪声发育.
对于简单的双层模型,我们使用(9)式作为梯度算子.图7a是真实反射率模型,图7b是常规全波RTM偏移成像的结果,而图7c、d分别是使用常规LSRTM方法和我们的方案迭代10次得到的反射率模型.显然,与RTM相比,LSRTM的偏移剖面振幅更加均衡,偏移假象也比较少.特别地,我们将常规LSRTM和基于Poynting矢量行波分离的LSRTM在收敛速率上进行了比较,如图8所示.可见,在相同的迭代次数条件下我们的方法模型预测误差更小.
2.2 Marmousi模型
本模型深度为1.5 km,宽度为4.0 km,具体速度参数如图9a所示.本实验采用主频为15 Hz,时间采样间隔为1 ms的雷克子波.炮点置于地表0 km至4.0 km处,炮间距设为200 m.检波点在地表均匀排列,间隔设为20 m,总记录时长为4 s.反演所用背景速度为图9b,模型真实反射率如图9c所示.

图5 双层介质中重构的震源波场(a)和经AGC处理后的检波器波场(b)其中蓝色箭头所指为背向反射波,红色线条表示反射界面.Fig.5 Reconstructed source wavefield (a) and receiver wavefield processed by AGC (b) in a two-layer modelBlue arrows point to the back-reflected waves, and red lines represent the reflective interfaces.

图6 不同成像条件单炮数据的成像结果(a)、(b)和(c)对应的偏移算子分别为(4)式、(9)式和(10)式.相较于全波成像条件,后两者没有低频噪声发育,因此剖面质量更高.Fig.6 Imaging results of single-shot data under different imaging conditionsThe migration operators corresponding to (a), (b) and (c) are equations (4), (9) and (10), respectively. Compared with full-wave imaging conditions, the latter two have higher-quality profiles without low-frequency noises.

图7 (a) 真实反射率模型; (b) 基于全波成像条件的RTM偏移结果; (c) 常规LSRTM迭代10次的反演结果; (d) 基于Poynting矢量行波分离的LSRTM方法迭代10次的反演结果Fig.7 (a) True reflectivity model; (b) Result of RTM with the full-wave imaging condition; (c) Inversion result after 10 iterations using the conventional LSRTM; (d) Inversion result after 10 iterations using LSRTM with the wavefield decomposition based on Poynting vector

图8 对于双层介质,常规LSRTM和基于Poynting矢量行波分离的LSRTM收敛性的对比(显然,我们方法的收敛速率更高,残差也更小)Fig.8 Comparison of convergence between conventional LSRTM and LSRTM with the wavefield decomposition based on the Poynting vector for the two-layer model(Note that our scheme has a higher convergence rate and a minor residual)

图9 Marmousi模型(a) 真实速度; (b) 偏移速度; (c) 真实反射率.Fig.9 Marmousi model(a) True velocity; (b) Migration velocity; (c) True reflectivity.

图10 Marmousi模型中的波场快照(a) 震源波场; (b) 经AGC处理后显示的震源波场; (c) 检波器波场.Fig.10 Snapshots of wavefield in the Marmousi model(a) The source wavefield; (b) The displayed source wavefield after the AGC process; (c) The receiver wavefield.

图11 Marmousi模型的偏移成像结果(a) 基于全波成像条件的RTM; (b) 常规LSRTM; (c) 基于Poynting矢量行波分离的LSRTM.其中,LSRTM的迭代次数为20.Fig.11 Migration results of the Mamousi model(a) RTM with the full-wave imaging condition; (b) The conventional LSRTM; (c) LSRTM with the wavefield decomposition based on Poynting vectors. Here, the iteration numbers of two LSRTM schemes are both 20.
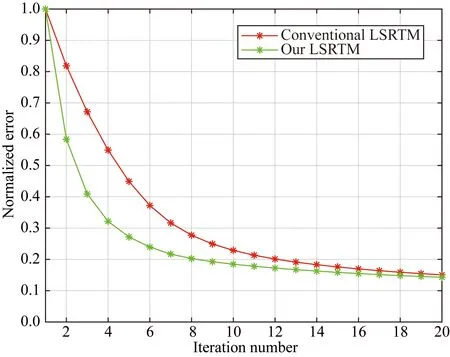
图12 对于Marmousi模型,常规LSRTM和基于Poynting矢量行波分离的LSRTM的收敛曲线Fig.12 Comparison of convergence between conventional LSRTM and LSRTM with the wavefield decomposition based on the Poynting vector for the Marmousi model
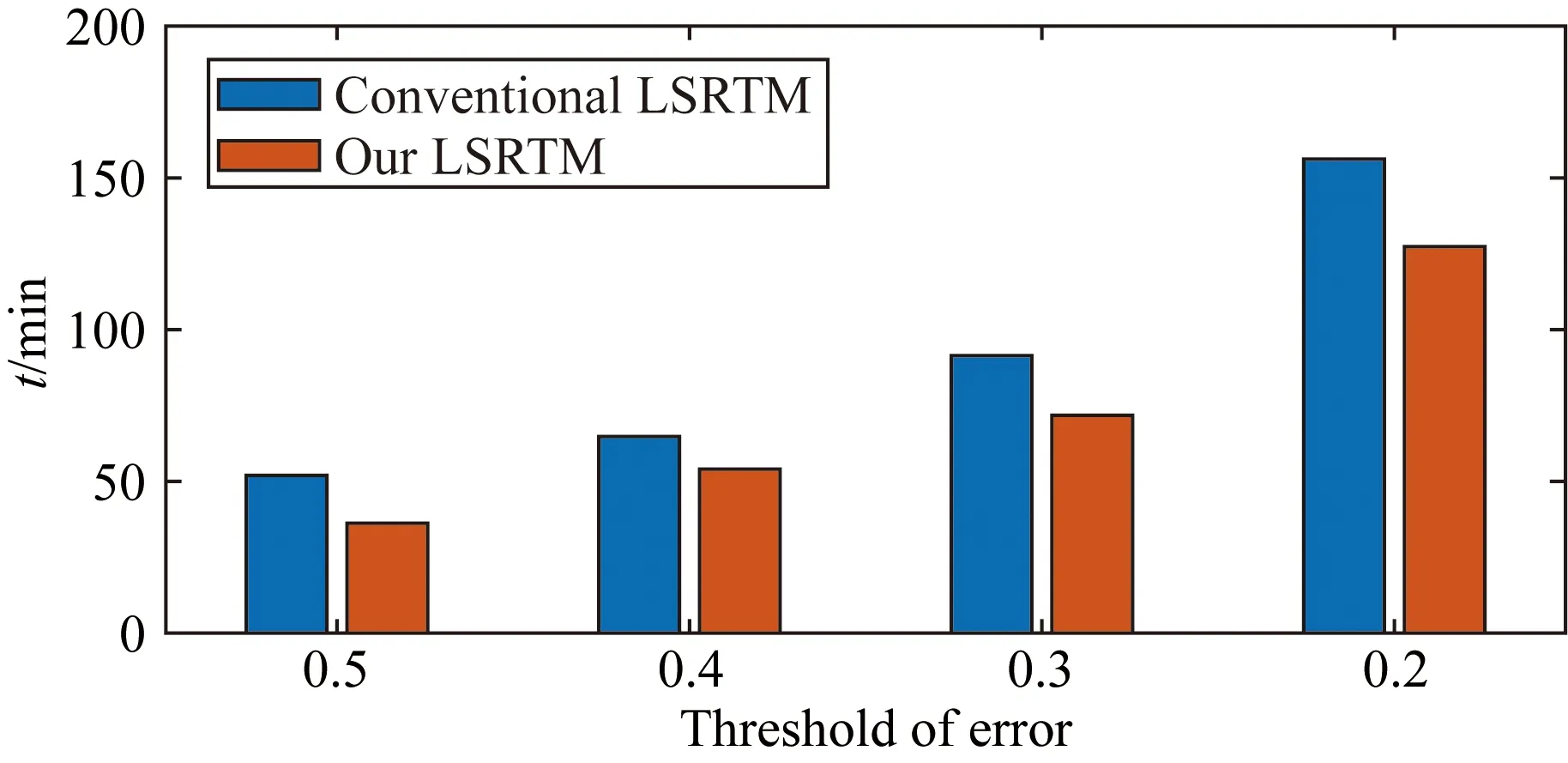
图13 常规LSRTM和基于Poynting矢量行波分离的LSRTM达到指定误差阈值所需时间Fig.13 Time required for conventional LSRTM and LSRTM based on the Poynting-vector wavefield separation to reach the specified error threshold
为了展示在光滑的背景速度下背向反射的发育程度和波场的混叠程度,我们分别记录了震源位于地表中央处时1.15 s时刻的震源波场和检波器波场.如图10a、c所示,因为界面附近的阻抗差异缩小,导致波场背向反射的能量弱化.这也是常规RTM得到的剖面上低频噪声并没有十分严重的原因(如图11a所示).为了展示背向反射,我们对震源波场快照进行了自动增益控制以增加较弱的反射能量,得到如图10b所示的结果.从中,我们可以发现在部分区域,波场的混叠比较严重,如图中所标注的A和B区域.以A区域为例,两种波发生了混叠但是都沿相同垂直向上方向,在此求出来的Poynting矢量仍能保持向上,因此其分离结果是准确的.而在界面处(B区域),入射波和反射波同时存在且垂直方向不同,但是因为入射波能量明显优于反射波能量,其Poynting矢量方向与入射波传播方向相近,因此采用(9)式或(10)式仍可以在此成像.
在此,我们分别使用RTM,常规LSRTM和基于Poynting矢量行波分离的LSRTM对地震数据进行了反演成像,并将结果展示在图11中.其中,LSRTM的迭代次数为20,我们的方法在前五次迭代中采用了(10)式作为梯度算子.相较于RTM方法,LSRTM的结果分辨率和信噪比得到了极大的改善.值得注意的是,与常规LSRTM结果相比,使用我们的LSRTM方法得到的剖面浅部噪声更少,成像轴清晰.图12展示了常规LSRTM和基于Poynting矢量的LSRTM在收敛性上的比较,结果发现我们的方案对于复杂的模型在收敛速率上依然优于常规的LSRTM.
除此之外,我们还对两种方案的运行时间进行了比较,结果发现:采用(9)式或者(10)式作为梯度算子,其运行时间大致为采用全波成像条件(4)式的1.375倍.相较于传统的全波LSRTM,我们的方案只在早期的迭代中增加运算量.假设最大迭代次数是n, 我们在前m次迭代中以(9)式或者(10)式作为梯度算子,常规方法中每次迭代需要时间为t,所以常规LSRTM所需总时长为nt,而我们的方法所需要的总时长则为nt+0.375mt.当n≫m时,程序所增加的时间可忽略不计.另外,将标准误差阈值分别设置为0.5、0.4、0.3和0.2,我们计算了传统LSRTM和基于Poynting矢量的LSRTM程序所需的时间长度,并将其展示如图13.可见我们的方法在加快收敛速率上具有明显效果.
3 结论
本文提出并实现了基于Poynting矢量行波分离的最小二乘逆时偏移方案.作为一种基于双程波的地震成像方法,LSRTM面临着背向反射所引发的强振幅噪声和虚假轴的干扰.低频噪声来自于背向反射波与正常传播的波之间的互相关,因此在梯度构建时选择不同垂直方向的波场组分进行互相关可以有效压制低频噪声.进一步地,在成像条件中只保留震源波场的下行组分和检波器波场的上行组分之间的互相关,虽然会使逆时偏移退化为类似于单程波偏移的方法,但是可以进一步地去除偏移假象.
借助Poynting矢量的方向指示性,对震源波场和检波器波场进行上下行波分离具有简单直接,方便快捷的优点.并且考虑到Poynting矢量对于重叠区域的效果不佳且不完全的成像条件也会损失波的部分有效信息,我们可以只在迭代的早期使用改造后的梯度算子.这样我们既充分利用了地震波所携带的有效信息,又降低了方法所需的运算成本.数值算例证明通过本文的方法,在减少迭代次数(运算量)的基础上,我们可以得到振幅均衡性好且信噪比更高的成像结果.

