基于主成分回归模型的建设工程项目成本预测研究

赵 晔 京鑫建设集团助理工程师，硕士研究生

1 研究背景

1.1 选题的研究背景和意义

随着政策的调整，曾经发展火热的建筑业的发展速度瞬间下滑。2015 年的触底反弹，给建筑行业发展带来了一丝信心，但并没有扭转行业低迷的态势。在这个重新洗牌、转型升级的关键阶段，承包商做好标前成本的预测显得更加重要。精确的成本预测可以为投标报价提供基础数据，进而影响承包商的中标结果和目标利润。通过成本预测模型的快速和高精度预测，有利于建筑施工企业对成本进行事前控制，规避经济风险，提高企业自身竞争力[1]。

1.2 建筑工程项目成本预测方法

建筑工程成本预测方法分为定性预测和定量预测两大类。定性预测法又称经验预测法，是目前大部分施工企业采用的成本预测方法，即通过有经验的项目经理根据市场行情估计项目未来的成本水平。这种预测方法在资料不多、难以进行定量预测时最为适用。从企业发展全局来看，现有的成本预测方法并不能对建筑施工企业工程项目的成本发展趋势做出科学估计。定量预测法是利用历史成本统计数据，建立成本预测模型，来推测和演算未来成本的可能结果。目前，国外的成本预测模型主要有BCIS 模型、Kouskoulas 估算模型、CBR 估计模型等数据分析模型。而国内学者在传统的成本估算法基础上建立了模糊类比估算模型、灰色预测法、BP 人工神经网络预测模型[2][3]。

由于影响建设项目成本的因素众多，为了能引入较多的因素且在尽量损失较少信息的前提下，研究建设项目成本预测，引入主成分分析法达到研究目的。

1.3 建立成本预测模型的重要意义

本文通过搜集施工企业已竣工结算工程的成本数据，初步选取影响工程成本的因素，基于主成分多元回归模型，建立施工企业建筑工程成本预测模型，以期能对项目成本的预测提高精确度，为管理者进行投资决策提供依据，为工程实施时资源计划制定提供借鉴，为管理人员控制成本提供成本计划指标。

2 数据分析模型建立

2.1 影响因素的选取

根据工程实体组成部分、工程成本的组成结构、辅助工程实体实现的基本条件，在查阅文献的基础上，确定影响建筑工程成本的影响因素包括建筑面积、施工工期、标准层建筑面积、建筑层高、建筑层数、门窗数量、当年工程造价指数、结构形式、地基类型、基础类型、门窗类型、屋面类型、外墙装饰、工程类别和楼面装饰15 个影响因素。

2.2 数据收集与处理

本文选取的数据为建筑工程项目竣工验收并竣工结算完成后的项目数据，经搜集和汇总获得了近3 年河北省几家施工企业的40 个已完工程的项目结算数据。从40个样本中选取对应因子的数据。因指标选取既有定量因素也有定性因素，为了保证在预测模型中各因子之间的可比性，对定性因素的样本数据进行量化处理，选取定性因素对应的分部分项工程的造价来进行计算。

2.3 主成分分析过程

观察获取的样本数据，各影响因素之间数量级差别很大且量纲不统一，为清除量纲的影响，将数据导入SPSS 软件后，首先对数据进行标准化处理，然后对变量进行多重共线性诊断。当存在多重共线性时引入主成分分析法，进行主成分分析前需要检验数据是否满足主成分分析分条件，再进行KMO 检验和Battle 检验，检验是否适合进行主成分分析，最后对主成分进行提取。

将数据导入SPSS 软件分析后，数据之间存在多重共线性，指标zx3、zx4、zx6、zx7、zx8、zx11、zx13、zx14和zx15的容忍度小于0.1，方差膨胀系数大于10，可以认为指标间存在多重共线性。引入主成分分析法解决这一问题，首先进行KMO 检验和Battle 检验，KMO 的检验值为0.820，大于0.5 的最低标准；Battle 的球形度检验的近似卡方值为799.520，达到显著性水平。综合可知，样本数据适合进行主成分分析。在检验满足使用主成分分析的条件后，需要对主成分进行提取。

通过总体方差表可得，第1 个主成分的特征根是9.13，方差贡献率60.868%；第2 个主成分的特征根是1.378，方差贡献率9.184%；第3个主成分的特征根是1.125，方差贡献率7.497%，3 个主成分的累计共线率77.549%。这进一步说明提取3 个主成分是比较合适的。一般认为累计贡献率在70%～90%是可以接受的。在确定提取前3 个主成分后，根据因子得分矩阵，进而写出3 个主成分的表达式：

2.4 主成分的回归模型

根据上面提取的主成分，建立标准化的因变量关于主成分的回归方程，得到主成分回归方程：

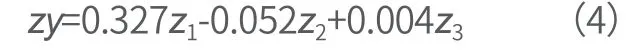
将式（1）、式（2）、式（3）带入式（4），并将回归方程中的zy还原成为标准化的y，将zxi还原成未标准化的xi，整理后即可得到因变量y 关于p 个自变量的回归方程：

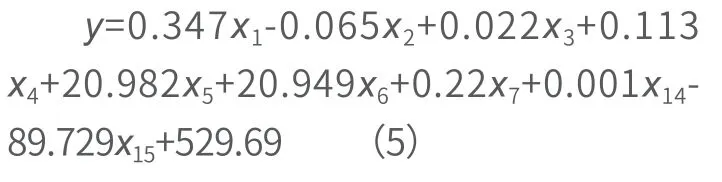
2.5 回归模型的检验

建立回归模型后，需要进行统计学检验以判断所建回归模型的显著程度、与原始数据的拟合程度。3 个主成分变量回归系数的P 值均小于显著性水平α，3 个主成分变量对因变量Y 均有显著性作用，VIF 值均小于10，不存在多重共线性问题。这说明主成分回归方程较好地解决了多元回归方程的多重共线性问题。

相关系数R 值为0 ～1，此模型的R值为0.990，说明自变量与因变量之间正相关。反映总体回归效果的决定系数R2＞0.8，回归效果较好，说明各自变量与因变量间具有较好的相关性，可以解释77.549%的信息。

3 实证分析

随机选取河北省3 个已建工程，根据预测公式计算项目估算值，将结果与项目工程实际造价进行对比分析，判断模型的可行性。经检测，项目1 预测造价1222.69，实际造价1291.86；项目2 预测造价1055.58，实际造价1134.58；项目3预测造价770.74，实际造价697.91。项目1、2、3 的工程造价与所建成本预测模型的计算值分别相差5%、6%、-9%，验证结果均在±10%以内，符合我国对拟建项目造价浮动±10%的规定，说明该成本预测模型预测结果可靠。

4 结论与展望

4.1 研究结论

本文首先简要叙述了成本预测模型的建立与研究现状，并对主成分分析法、多元回归分析法做简要介绍。然后通过相关文献的研究和专家咨询，汇总得出影响工程成本的影响因素，对施工企业成本预测模型的建立过程、操作步骤进行详细论述。最后用已完工程数据检测预测模型的可靠性。通过模型建立和检验，证明模型的易用性和精确性。承包商可以在招投标过的程中运用此模型进行成本预测，这对投标定价、目标利润制定、事前成本控制有重要意义。

4.2 研究不足与展望

首先，本文选取的数据仅局限于河北省，由于每个省份计价方式有些许不同，导致本模型不具有广泛的适用性。其次，本文研究选取的成本影响因素静态多动态少，一定程度上影响模型预测的精确度。最后，虽然模型预测结果的误差控制在了我国制定的标准以内，但是对于制定目标利润并不能提供很好的依据。

基于此模型，可以扩展到全国区域，并经过优化成本影响因素的选取，对模型进行修正，降低误差，建立适用于全国范围内的成本预测模型。