基于负荷重要性和源-荷互补性的离网系统终端电/热/冷负荷投切策略

刘小龙 李欣然 刘志谱 卢颖华 罗 真

（湖南大学电气与信息工程学院 长沙 410082）

0 引言

传统能源短缺问题越来越受到关注，为了能够高效、可持续地利用多种能源，综合能源系统（Integrated Energy System, IES）成为了研究热点之一[1-4]。目前有较多考虑需求侧响应的 IES优化运行的研究[5-6]，该方面的研究需要转移负荷或改变生产安排，且优化对象多为长时间尺度并网运行系统。离网情况下应更多地考虑负荷重要性，并充分利用有限能源尽量保证负荷正常工作和提高负荷恢复量。目前有较多学者针对离网状态下负荷恢复量的优化问题进行研究。文献[7]提出了一种自动恢复算法，能够有效增加负荷的恢复数量，同时保证开关操作次数尽量少。文献[8]提出了一种基于自适应多目标协调搜索算法的孤网系统重构方法，该方法在提高系统负载能力的同时可降低功率损耗。文献[9]考虑分布式发电机组的下垂特性及可再生能源发电、负荷和配电馈线参数的不确定性，提出了一种全局灵敏度分析方法来评估可变能源对孤网系统最大负载能力的影响。文献[10]在考虑负荷需求和可再生能源发电不确定性的基础上，提出一种兼顾经济排放与负载能力的优化运行方法。文献[11]提出一种兼顾燃料消耗最小化、切换操作成本最小化以及负载能力最大化的孤网系统优化重构方法。上述研究工作主要从提高离网系统短时间的负荷恢复量或长时间的经济性的角度考虑，是某一个时间尺度的优化，不适用于制定多时间尺度的负荷投切方案。同时，此类研究并没有对负荷的重要程度进行评估[12-13]以确定负荷投切的优先级，不够全面。

综合分析，目前的研究或是从提升负荷恢复量的角度优化投切，或是按照负荷重要性确定投切方案。由于源、荷之间的供需不平衡以及新能源出力的随机波动性，仅从某一个方面优化容易导致负荷投切频繁或能源利用率不高，导致该问题的根本原因在于重要性高的负荷，源、荷之间的互补性不一定好。基于此，本文在考虑负荷重要性指标的基础上引入源-荷互补性指标，提出一种基于综合指标的多时间尺度负荷投切策略。同时，充分利用储能的时空转移特性[14-16]以及温控负荷的需求弹性特点[17-18]，缓冲短时供需不平衡，以优化负荷投切策略。进一步，考虑到预测偏差对离网系统的影响较大，本文在确定负荷投切方案和能源调度方案后，利用基于模型预测控制的滚动优化方法跟踪计划值，维持最优方案。

1 离网系统结构

本文研究的离网系统包括电/热/冷供能设备及相应终端负荷，结构如图1所示。以夏季典型日为例，脱网情况下可利用系统中的可再生能源、电/冷储能、燃气机、电制冷机以及冷温水机供应负荷。对于一级重要负荷，始终保持供能，开关/阀门处于闭合状态，对于二级重要负荷，通过本文策略控制其开关/阀门状态，实现各个独立负荷的优化投切。

图1 系统结构Fig.1 The structure of system

2 指标定义

2.1 负荷重要性指标

负荷的重要程度与用户供能可靠性的要求和用户中断供能产生的危害程度等因素相关。本文采用专家打分的方式对各分项指标进行打分，然后通过熵权法确定各分项指标所占权重，最后计算出各负荷的重要性指标。本文根据负荷重要程度的特点选取了负荷敏感程度、负荷规模、负荷损坏程度等五个分项指标共同构建负荷重要性指标，如图2所示。为了给专家打分提供统一的参考标准，将指标的严重程度（可能性）划分为4个等级，并确定了各等级的打分范围，见表1。

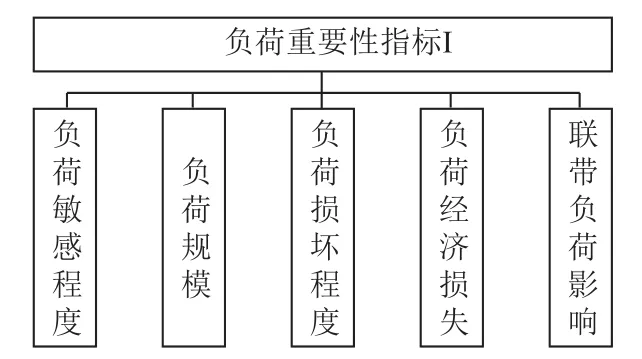
图2 负荷重要性指标的构建Fig.2 The construction of load importance index

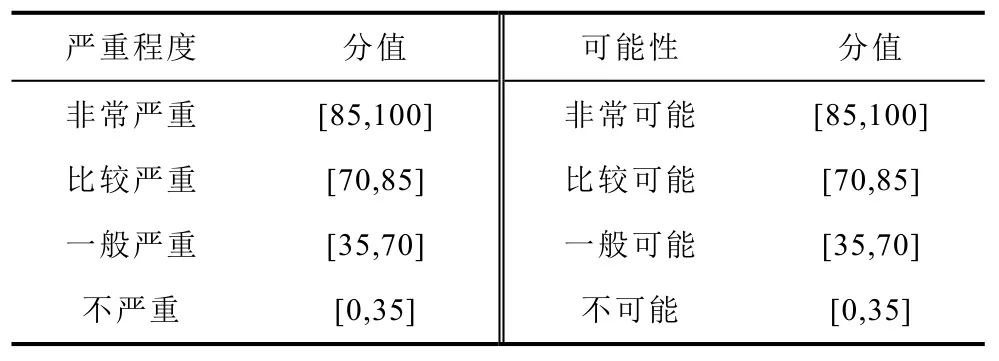
表1 指标打分参考分值Tab.1 Index scoring reference score

2.2 源-荷互补性指标

为了评价源、荷之间的互补性程度大小，定义互补性指标以量化源-荷之间有功功率的互补能力。

式中，β为源、荷功率变化率之差的绝对值的相反数；γp、γl分别为源、荷功率的变化率；Pp、Pl分别为源、荷功率；T为采样周期；i为第i个采样时刻。当β＝0时，说明此时源、荷的 1阶变化量方向相同、数值相等，变化量恰好完全抵消，达到完全互补；当β＜0时，说明此时源、荷的1阶变化量存在未抵消部分。β值反映了源、荷互补的程度，β越大，源-荷互补程度越好，β越小则源-荷互补程度越差。

图3 不同采样周期下的源、荷功率波动示意图Fig.3 Schematic diagram of source and load power fluctuation under different sampling periods

然而，源-荷互补程度还与采样周期T的大小有着密切的联系，如图3所示，采样周期T=TL时，源-荷波动曲线为虚线部分所示，此时负荷B与源的互补程度更好。采样周期T=TS时，源-荷波动曲线为实线部分所示，此时，在部分短时间尺度内，负荷A与源的互补程度更好。为了更加准确地评价源-荷互补程度，本文综合考虑长、短两种采样周期的源-荷互补特性。当源/荷整体波动较大，应重点考虑整体互补程度。反之，应重点考虑源/荷局部互补程度。基于此，本文根据源/荷整体、局部波动情况设置长、短采样周期的互补性指标权重。方差描述和中心偏离的程度，通常用来衡量数据波动大小。同时，考虑源、荷组合过程中的互补性效果主要受波动程度最大的源/荷影响，本文根据长（短）采样周期下源与负荷方差中的最大值确定长（短）采样周期的互补性指标权重。

根据以上分析，本文综合考虑源、荷整体与局部上的互补程度，定义互补性指标，如式（2）所示。互补性指标越大，说明源-荷功率变化趋势越接近，互补程度越好；反之，说明源-荷的互补程度越差。

式中，Ea～b为在a～b时段内的源-荷互补性指标，描述源-荷互补程度的平均效应；第一个等式右侧的两部分分别表示整体、局部的互补程度；分别为整体、局部互补程度的权重，为源与负荷预测功率的方差中的最大值，为源与负荷期望功率波动分量的方差中的最大值；i、j为采样时刻，K为源与负荷总数；PF、PE分别为源/荷预测值与期望波动分量；Fμ、Eμ分别为源/荷预测值与期望波动分量的平均值。

考虑到日前预测精度[19]，设置TL＝15min。通过对负荷的类型及其特征进行统计分析，负荷在1min之内的波动不明显，采样周期取1min能够较好地描述局部波动特征，因此设置TS=1min。采样周期为TL的源、荷数据可根据预测信息确定（考虑到源/荷预测值在文中的主要作用是衡量整体变化趋势，同时避免预测精度对指标产生影响，本文预测值均采用最小二乘法进行多项式曲线拟合）。采样周期为TS的数据无法准确预测，本文按照期望功率的波动分量计算，计算步骤如下：①统计采样周期为TS的每一个采样点在一年内的有功功率值，然后计算每一个采样点有功功率的期望值；②根据所有采样点的期望值得到采样周期为TS的期望功率曲线；③利用一阶差分提取期望功率曲线的波动分量，将该值作为期望波动分量。

可再生能源的功率值与气候相关，即某一采样点的历史有功功率值分布较分散，只能得到一个置信度较差的期望波动分量值，在该情况下计算出的源-荷局部互补性指标不能够反映真实的局部互补特性，因此，本文不考虑风/光可再生能源的期望波动分量。

2.3 综合指标

为了能够综合性地描述负荷的重要程度及负荷与源的互补程度，本节根据2.1节、2.2节定义的负荷重要性指标以及源-荷互补性指标，综合考虑二者的影响程度，定义综合指标Za～b为

式中，I为负荷重要性指标；λI、λE为权系数，分别表示负荷重要性与源、荷互补性的相对重要程度，λI,λE＞0 且λI+λE=1。

为了更客观地得到负荷重要性与源-荷互补性的权重，本文采用熵权法确定其权系数λI、λE。熵权法[20]根据各指标的变异程度，利用信息熵计算出各指标的熵权，再通过熵权对各指标权重进行修正，从而得到较为客观的指标权重。具体计算步骤本文不再赘述。

3 基于综合指标的负荷优化投切策略

3.1 单时间尺度供能情况下的投切策略

离网情况下，为了维持正常的生产工作，负荷的连续供能时间越长越好，本文定义负荷在脱网的整个时间段内连续供能为单时间尺度供能。本文提出基于单时间尺度供能和综合指标的负荷优化投切策略，其思路如图4所示。

本文采用启发式算法按照综合指标由大到小的顺序确定负荷投切方案。在逐步确定供应负荷的过程中，源与已供应负荷的功率差值会随之改变，因此需要滚动更新综合指标，通过不断更新迭代，最终确定离网期间最优的负荷供应方案。单时间尺度供能情况下的负荷投切策略核心步骤如下。

1）定义系统中所有二级负荷构成的集合为CL。计算初始净电功率（式（1）、式（2）中的“源”）为

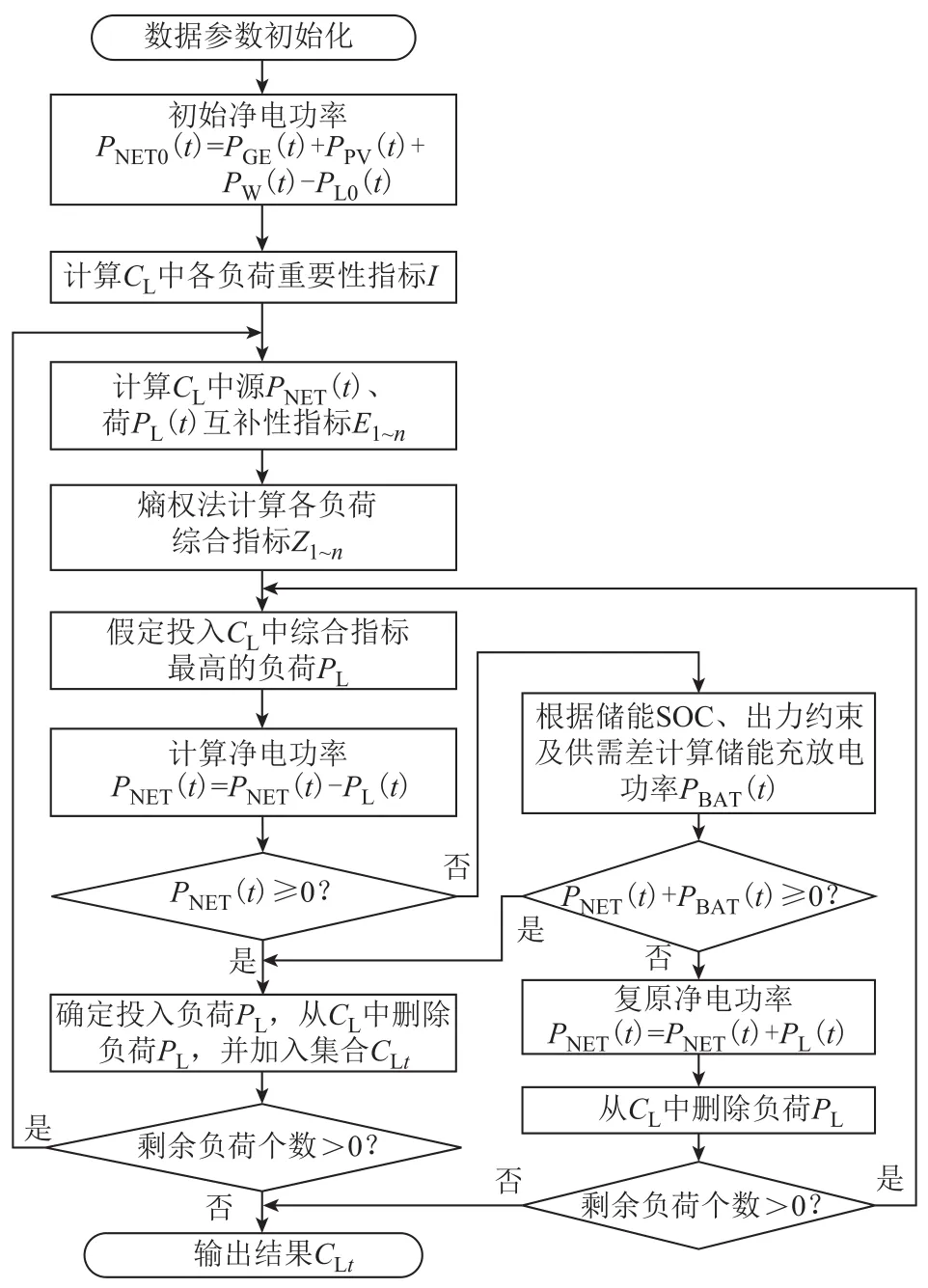
图4 基于单时间尺度供能和综合指标的负荷投切策略Fig.4 Flow chart of load switching strategy based on single time scale energy supply and comprehensive index

式中，t为采样时刻；PNET0为初始净电功率；PGE为除去备用和输送冷（热）能所需电耗后燃气机可利用功率；PW、PPV分别为风/光最大可利用功率；PL0为一级负荷需求功率；PGE.max为燃气机额定功率；PS为燃气机保留的备用；PPUMP为输送冷（热）能所需电耗。

2）源、荷互补性指标和综合指标计算。

3）投入CL中综合指标最大的负荷PL。重复步骤2）和步骤3），达到边界条件后输出结果。

3.2 多时间尺度供能情况下的投切策略

确定可供应的单时间尺度负荷后，可能存在部分剩余电能未被利用，其能源利用效率不是最高的情况。为了能够在尽量保证负荷正常工作的前提下提高能源的利用效率，同时减少负荷投切频次，较优方案为首先充分投入单时间尺度负荷，在此基础上继续投入其余时间尺度负荷。确定单时间尺度负荷供应方案后，可能存在多个剩余电能区域，由于预测精度的原因，时段靠后的区域的剩余电能预测误差相对较大，因此优先确定靠前时段的负荷供应方案，在此基础上，更新预测值，确定靠后时段的负荷供应方案。

根据以上分析，本文提出基于多时间尺度供能和综合指标的负荷投切策略，其流程如图5所示，核心步骤如下：①定义剩余未投入的负荷构成的集合为；按照时间先后顺序搜索可投入负荷的最大时间尺度；②按照综合指标由大到小的顺序确定中能够投入的负荷及其投入时刻集合；③在整个离网时段的起始时刻投入CLt中的所有负荷，并按照中记录的各个负荷及其投入时刻，逐渐投入多时间尺度负荷。

图5 基于多时间尺度供能和综合指标的负荷投切策略Fig.5 Flow chart of load switching strategy based on multi- time scale energy supply and comprehensive index

该策略中，储能需要同时满足单时间和多时间尺度负荷需求。为了避免储能容量集中用于局部时段，充分发挥其在整个离网时段内的时空转移能力，本文制定如下储能灵活调度规则，作为策略中的约束条件。

1）若τ～τ+k时段内供需平衡且储能存在放电状态，则不考虑在该时段内投入多时间尺度负荷，其余情况则利用净电能和储能在该时段内投入多时间尺度负荷。该规则通过投入多时间尺度负荷以避免储能集中充电。

2）在投入多时间尺度负荷的过程中，若τ～τ+k时段内的净电功率存在大于0的状态，则利用净电能和储能继续投入多时间尺度负荷，其余情况不再利用储能投入多时间尺度负荷。该规则在充分投入多时间尺度负荷的情况下避免储能集中放电。

3.3 温控负荷投切策略

与电负荷的投切策略类似，同样可采用综合指标投切策略制定冷（热）负荷供应方案。园区一级重要温控负荷由电制冷机供应，保证供能的可靠性。在此基础上，在冷温水机可输出的最大能量范围内按照综合指标大小依次确定可供应的二级温控负荷，同时，利用冷（热）储能实时调节供需平衡。该思路具体步骤与电负荷的相似，不再展开。温控负荷投切策略的独特之处在于，温控负荷存在需求弹性的特点，在一定的舒适度范围内调节温度，能够缓冲短时间内的供需不平衡。参考文献[18]并根据能量守恒定理，可知温控负荷温度的变化与当前调度时段室内空气热量、供冷/热量以及室内外传递的冷/热量有关，其关系可表示为

式中，cair、mair分别为室内空气比热容、质量；分别为调度时段的室内、室外温度；为单位时间向室内的供冷/热量；k0、A、D分别为墙体的热传导系数、面积和厚度。

为了保证冷（热）负荷的正常供能，燃气机将提供部分电能给水泵等电耗设备以输送冷/热能。本文假设该部分电能的大小与冷/热负荷需求近似成正比关系，即

4 基于MPC的滚动优化调度

离网状态下通常利用储能的快速响应能力平抑非计划波动。当离网时长较大时，累积预测误差较大，导致储能荷电状态（State of Charge, SOC）偏离计划值较大，该情况下可能无法满足本文方案所计算出的负荷需求。本文通过基于模型预测控制（Model Predictive Control, MPC）的滚动优化调度方法减少不确定性因素，跟踪储能SOC计划值。MPC是不断局部优化和不断滚动实施控制作用的交替过程，具体可参照文献[21-22]，本文不再详细介绍。

储能 SOC计划值根据上文投切策略确定，如图 6所示。首先根据源/荷预测、储能容量等信息确定单时间尺度负荷投切方案。在此基础上，根据更新的预测信息以及多时间尺度负荷投切策略计算当前至结束时段内能源调度方案与负荷投切方案。将其中的储能SOC作为基于MPC优化调度的计划值，结合超短期预测信息以及目标约束确定实时调度方案。

图6 基于MPC的滚动优化调度与负荷投切策略关系Fig.6 Relationship between load switching strategy and rolling optimal scheduling based on MPC

以夏季供冷为例，根据离网系统各变量之间的关系，建立MPC算法的状态空间模型，如式（7）、式（8）。基于可再生能源以及负荷的超短期功率预测数据，并对上述状态空间模型反复迭代，可得到电储能与冷储能 SOC在控制时域mΔt内的预估输出值构成的向量Yf。取当前时刻向前mΔt时段内，电储能与冷储能 SOC计划值构成的向量Rref为跟踪控制目标。YfRref如式（9）所示。以电储能与冷储能 SOC预估输出值与计划值之间的误差最小为目标，同时保证各机组控制调节增量尽量小，将日内滚动优化调度转换为如式（10）所示的二次规划问题。二次规划模型通过调用 Matlab二次规划quadprog函数进行求解。

式（7）中，状态量x(k)由燃气机功率(PGE)、电储能功率(PBES)/电储能 SOC(SBES)、联络线功率（Pgrid=0）、电制冷机功率(QEC)、冷温水机功率(QAC)以及冷储能功率(QCES)/冷储能SOC(SCES)构成；控制量由燃气机(ΔPGE)、电/冷储能(ΔPBES/ΔQCES)以及电制冷机(ΔQEC)的出力增量构成；扰动量由电/冷负荷(ΔPL/ΔQL)、可再生能源超短期预测功率(ΔPRE)增量构成；Δt为调度周期；Wpn、Wqn为电、冷储能额定容量；ηac为燃气机出力与冷温水机出力比例系数、ηec为电制冷系数。式（8）中，输出量y(k)为电储能SOC与冷储能SOC。式（10）中，H为电储能SOC跟踪误差与冷储能SOC跟踪误差的权重系数矩阵；U为控制量；Q为控制量的权重系数矩阵；A、b为不等式约束中的系数矩阵；Aeq、beq为等式约束中的系数矩阵；ub、lb分别为变量的上、下区间，考虑到篇幅限制本文不再具体描述。

5 仿真分析与验证

以夏季典型日进行仿真分析，系统中各设备参数配置见表2。电储能、冷储能能量状态约束范围分别为[0.1,0.9]、[0,1]，设置储能能量状态初始值为0.7。

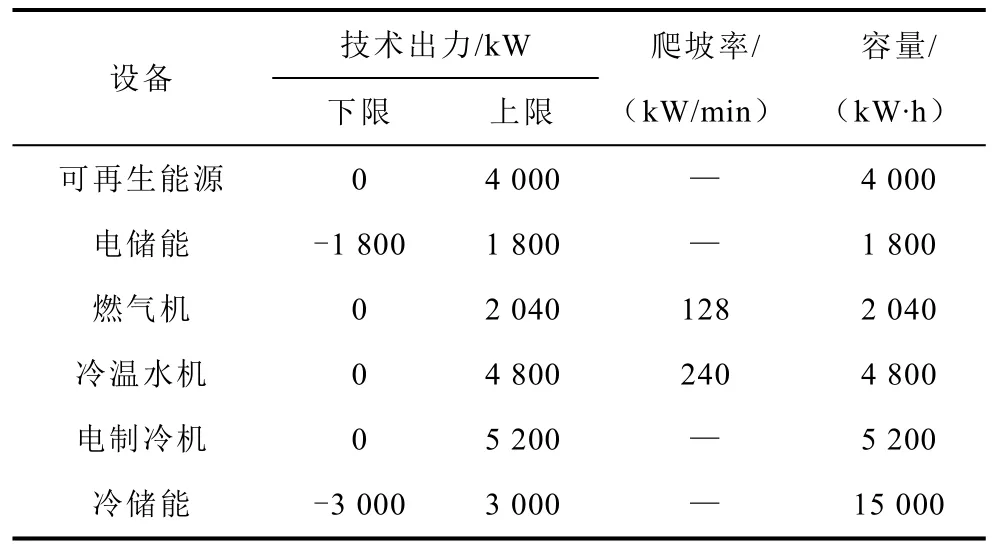
表2 系统参数配置Tab.2 The parameter configuration of IES

5.1 指标分析

本文选取系统中的10个二级电负荷和10个二级冷负荷作为研究对象。以电负荷为例，按照本文2.1节指标定义的方法计算出各负荷的重要性指标见表3。

表3 各二级负荷重要性指标Tab.3 The importance index of each second class load

按照本文2.2节、2.3节指标定义的方法计算出各负荷的第 1次互补性指标和第1次综合指标见表4。表中重要性指标I、互补性指标E均按照式（4）进行了标准化。可以看出负荷6的重要性指标最大，然而其互补性指标极小，因此其综合指标位于第二。第一则由重要性和互补性都较好的负荷10取代。负荷7的重要性虽然较高，然而其互补性却很低，因此其综合指标为第三。由此可见，综合指标的提出，从理论上可以改善因负荷（二级）重要程度稍高、源-荷互补程度很低而导致的能源无法充分利用的问题。

表4 各二级负荷第1次综合指标Tab.4 The first comprehensive index of second class load

5.2 单时间尺度供能仿真分析

首先针对电负荷的单时间尺度供能进行仿真分析，设置两组仿真实验：第一组实验分析长时间尺度脱网(24h)情况下的连续供能情况，策略Ⅰ根据重要性指标确定负荷供应方案，策略Ⅱ根据本文所提综合指标确定负荷供应方案；第二组实验分析短时间尺度脱网(2h)情况下的连续供能情况，策略Ⅰ、策略Ⅱ同上。

第一组实验结果如图7所示。柱状条表示储能充放电功率，放电为正。策略Ⅰ供应负荷6、7、10、5，供应负荷容量为85 155kW·h。剩余未被利用电能较多，最大供需差为2 480kW。策略Ⅱ供应负荷10、6、5、2、1，保证了重要性较高的负荷 6和 10，供应负荷量增加为 97 851kW·h。最大供需差减少为1 006kW，剩余未被利用电能大幅度减少。可知，策略Ⅱ利用了源、荷互补特性显著降低了供需不平衡的问题。另外，在储能调节过程中，策略Ⅰ中部分时段的储能充放电深度明显大于策略Ⅱ。进一步，对比策略Ⅰ和策略Ⅱ在供应上述负荷时储能荷电状态变化与所配置容量的关系，结果如图 8、图 9所示。

图7 长时间尺度脱网情况下策略Ⅰ、Ⅱ的负荷供应方案Fig.7 Load supply scheme of strategiesⅠand Ⅱ under long time scale off grid condition

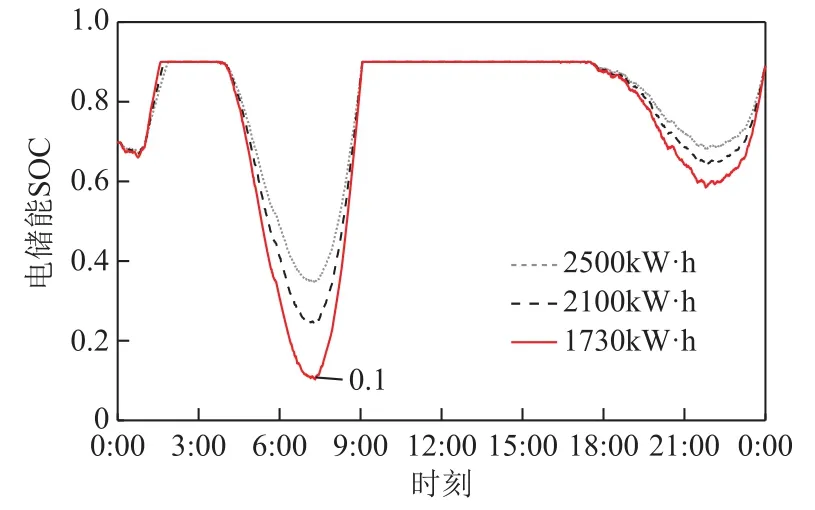
图8 策略Ⅰ电储能SOC变化与配置容量关系Fig.8 Relationship between BES SOC change and configuration capacity in strategyⅠ

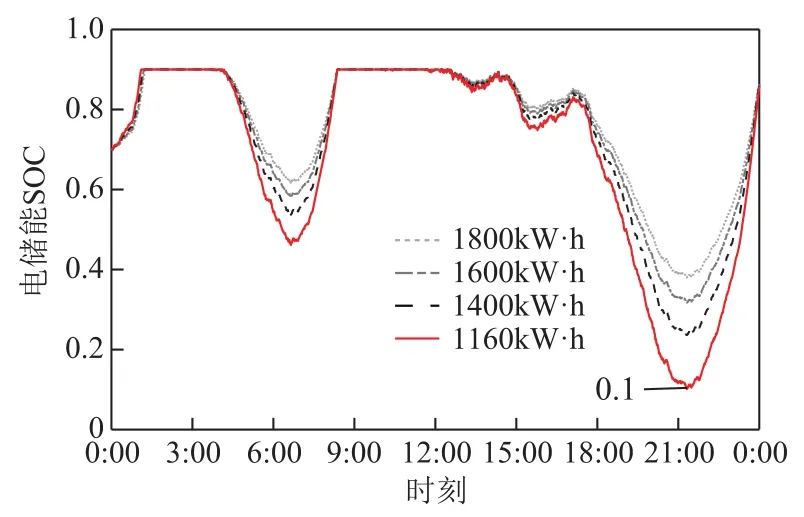
图9 策略Ⅱ电储能SOC变化与配置容量关系Fig.9 Relationship between BES SOC change and configuration capacity in strategyⅡ

由图 8、图 9可知，当储能配置容量相当时，两种策略在供应各自负荷时（策略Ⅱ供应负荷容量更多），策略Ⅱ储能SOC变化范围明显小于策略Ⅰ，即策略Ⅱ储能的裕量更大。从另一个角度来说，策略Ⅱ可以减少储能的配置容量，从图中可看出，策略Ⅰ的储能最低配置容量为 1 730kW·h，策略Ⅱ将储能最低配置容量降低到了 1 160kW·h，能够节约一定成本。

第二组实验结果如图10所示。策略Ⅱ供应负荷数量和供应负荷容量均显著高于策略Ⅰ，且策略Ⅱ供应了重要性排名前三的负荷。通过储能充放电调节，策略Ⅱ充分利用了几乎所有电能（包括储能电能），负荷能量利用率较高，而策略Ⅰ存在剩余未被利用电能，负荷能量利用率较低。另外，相比于策略Ⅰ，策略Ⅱ储能的充放电分布较均匀且充放电功率较小，说明其源、荷之间的贴合度更好，降低了储能调节的负担。

图10 短时间尺度脱网下策略Ⅰ、Ⅱ的负荷供应方案Fig.10 Load supply scheme of strategies Ⅰ and Ⅱ in case of short time scale off grid

两组实验的策略Ⅰ和策略Ⅱ各项数据对比结果见表5。可以看出，第一组实验的策略Ⅱ比策略Ⅰ负荷供应数量提升25%，其负荷能量利用率（供应负荷所用能量与总能量之比）由83%提升到95%。同时，最大供需差大大降低，降幅达60%，储能最低配置容量由1 730kW·h降低到1 160kW·h，降低了 33%，储能充放电深度降低 13%。第二组实验的策略Ⅱ比策略Ⅰ在负荷供应数量、负荷能量利用率、最大供需差以及储能充放电深度上均有显著优势，由于策略Ⅰ并未充分利用储能，其最低配置容量可以达到更低值。综上分析，满足负荷单时间尺度连续供电时，策略Ⅱ比于策略Ⅰ具有明显的优势。

表5 策略Ⅰ与策略Ⅱ对比结果Tab.5 Comparison between strategyⅠand strategyⅡ

下面针对冷负荷的单时间尺度供能进行仿真分析，以长时间尺度(24h)为例。冷负荷波动较小，功率值基本等同于预测值。按照本文策略确定的负荷供应方案如图 11所示，供应负荷7个，总负荷量116 970kW·h。冷储能蓄放能调节供需平衡，最后储能能量状态为0.14，负荷能量利用率98%。从图中可知，供应长时间尺度负荷后，电能全部被充分利用，无需进一步供应其余时间尺度负荷。原因有三个方面：①根据综合指标供应负荷，使最终的源、荷互补程度达到较好的效果，减少了供需差；②冷储能容量较大，可以通过蓄放能最大限度调节供需平衡；③利用温控负荷需求弹性的特点，当储能无法调节至供需平衡时，可在合理的舒适度范围内调节负荷的温度，起到短时缓冲供需不平衡的作用。按照重要性指标确定的供应方案同样会出现负荷能量利用率低，存在供需差等问题，在此不再具体讨论。

图11 本文策略冷负荷供应方案Fig.11 Cooling load supply scheme of this strategy

5.3 多时间尺度供能仿真分析

该部分针对基于多时间尺度供能和综合指标的负荷投切策略进行仿真分析，温控负荷单时间尺度已达到供需平衡，因此只对电负荷进行分析。假设脱网时长为24h，设置两种对比策略：对比策略1，将24h拆分为24个相等时段，根据重要性指标逐时段确定负荷供应方案；对比策略2，根据本文提出的多时间尺度供能方法和重要性指标确定负荷供应方案。三种策略的对比结果如图12所示。由图12a可知，策略1在每个时段都充分利用了电能，最大供应负荷数量达到了图中所示的8个。全时段总的负荷供应量PLS为101 930kW·h，负荷能量利用率98%。由图12b可知，策略2在供应长时间尺度（24h）负荷 6、7、10、5的基础上，继续供应多个短时间尺度负荷，但是在3:00～04:00和14:00～15:00两个时段存在部分剩余电能未被利用，总的负荷供应量为101 250kW·h，负荷能量利用率 98%。由图 12c可知，本文策略在供应长时间尺度负荷的基础上，继续供应了三个短时间尺度负荷，电能在所有时段被充分利用起来，本文策略总的负荷供应量为102 330kW·h，负荷能量利用为99%。

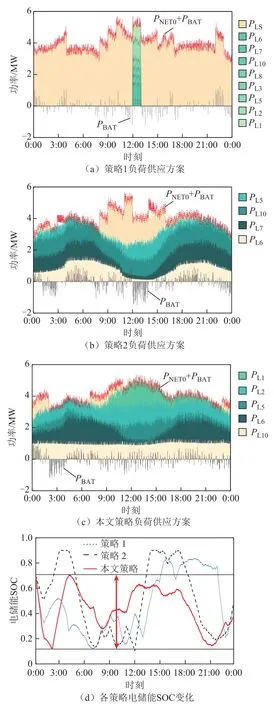
图12 多时间尺度供能情况下策略1、策略2及本文策略负荷供应方案以及电储能SOC变化Fig.12 Strategy 1, 2 and this paper load supply scheme and BES SOC change in the case of multi time scale energy supply

从各策略负荷供应量和能量利用率看，无明显差别，然而通过统计全时段内各策略的负荷投切情况（表6），策略 1的负荷投切次数累计达到11次之多，会对负荷的正常工作产生较大影响。究其原因，策略1只根据当前时段供需差以及储能状态确定负荷供应方案，容易在不同时段过渡时出现负荷投切的情况。从图12d中可以看出，在12:00之前和之后两个区域内，策略1的储能SOC只在较小范围内波动，没有充分发挥储能的时空转移能力。策略2的负荷投切次数为8次，对负荷本身和系统也会产生较大影响。主要原因在于已供应的长时间尺度负荷与源之间的贴合度较低，需要较多的短时间尺度负荷填补剩余未被利用电能。相比于以上两种策略，本文策略确定的负荷投切次数为4次，显著减少。从图12d中可以看出，本文策略的储能SOC分布较均匀且变化幅度不大，说明按照本文提出的储能灵活调度规则调节供需平衡，可在整个调度周期内充分发挥储能的时空转移能力，在一定程度上辅助综合指标投切策略降低负荷投切次数。

表6 策略1、策略2以及本文策略负荷投切情况Tab.6 Strategy 1,2 and this paper load switching

表6中，策略1起始时段（0:00～1:00）供应负荷为6、7、10、8、9，策略2起始时段供应负荷为6、7、10、5，本文策略起始时段供应负荷为10、6、5、2、1。搜索精度设置为1h，每经过1h更新负荷供应情况，表中“+”、“-”分别表示在前一时段基础上投切负荷。

5.4 MPC滚动优化调度仿真分析

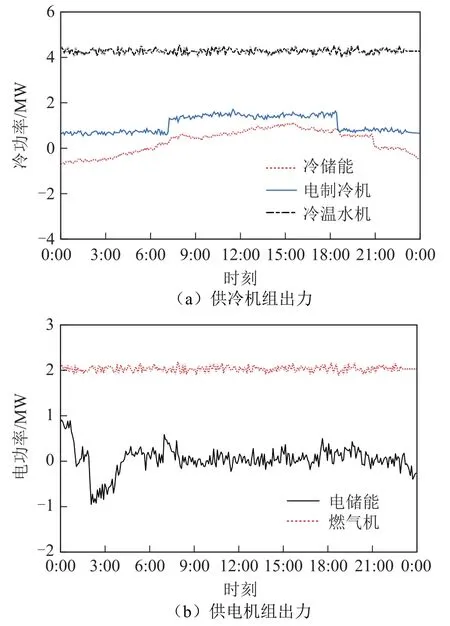
图13 日内实时调整后的机组出力Fig.13 Unit output after real-time adjustment in a day

图14 MPC优化后，储能能量状态跟踪计划值情况Fig.14 Status tracking plan value of stored energy after MPC optimization

该部分针对MPC优化调度进行仿真分析，MPC滚动优化的预测时长为1h，控制时长为30min，滚动优化调度执行周期为5min。通过MPC滚动优化得到的燃气机、电/冷储能、电制冷机及冷温水机的实时出力如图13所示。可知，为保证储能SOC跟踪计划值，实时调度将对调度计划进行一定程度的修正，保证各机组的调整增量始终保持在最小。图14a、图14b对比了 MPC优化前后冷储能能量状态和电储能SOC跟踪情况。无优化时，预测误差全部由储能调节，前段时间累计误差不大，储能能量状态偏离计划值较小。随着时间推移，累计误差逐渐增大，电储能SOC偏离计划值较大，部分时段甚至超出了电储能的调节能力范围。冷负荷的波动较小且冷储能容量较大，可以容纳较大的误差，因此能量状态偏离计划值不是特别明显。优化后，电储能SOC和冷储能能量状态与计划值基本吻合，尤其是电储能的优化效果非常明显。根据以上分析，通过MPC实时滚动优化，可实时跟踪储能能量状态计划值，维持最优负荷投切方案。

6 结论

综合全文分析，无论针对长时间尺度连续供能还是短时间尺度供能或者多时间尺度供能，本文所提策略都要优于基于重要性指标的负荷投切策略。本文的研究工作可总结为以下几个方面：

1）定义了负荷重要性指标以及源-荷互补性指标，在此基础上利用熵权法确定了综合指标。

2）提出基于多时间尺度供能和综合指标的离网系统终端电/热/冷负荷投切策略，并利用制定的储能灵活调度规则以及温控负荷的弹性需求特征辅助综合指标投切策略。所提策略能够有效解决了源-荷之间的不匹配问题，在提高离网系统能源利用效率的基础上，显著降低了负荷投切频次。

3）利用基于模型预测控制的滚动优化方法，实时跟踪储能能量状态计划值，维持最优负荷投切方案。