铜铝复合板渐进成形回弹缺陷研究
秦 勤 何 流 李 程 臧 勇
1.北京科技大学机械工程学院,北京,1000832.北京科技大学顺德研究生院,佛山,520300
0 引言
复合材料板材结合了基层材料的物理、化学和机械性能等优点,比单一金属板材具有更好的热膨胀性、强度、导电性、耐腐蚀性等性能,被广泛应用于汽车、航空航天、船舶、电力等工业领域[1-3]。对于传统成形工艺来说,模具的高昂成本决定了这些技术适合于大批量生产同类产品,不适合多品种小批量的生产需求,而渐进成形工艺作为一种无模柔性成形技术可以很好地适应这一需求,模具成本大大降低,近年来被广泛采用。因此复合板渐进成形工艺非常适合对材料性能有更高要求并且具有多品种小批量特征的高精尖制造业[4-6]。但在成形过程中,回弹缺陷成为影响零件成形精度的主要问题之一。
回弹缺陷是由多种工艺参数共同影响造成的,仅依靠试验无法得到各参数的具体影响情况,引入数学分析方法可以很好地解决参数影响的灵敏度问题。崔震等[7]、 RADU等[8]针对单板渐进成形回弹问题,利用简单试验法分析了部分成形参数对鼓包高度问题的影响规律,并通过方差分析方法分析了不同参数对鼓包高度影响的灵敏度,提出将多种工艺参数组合从而有效减小回弹量的方法。 HUSSAIN等[9]通过试验分析了铝板渐进成形中的回弹现象,并讨论了各工艺参数对回弹缺陷的影响,通过数学分析方法提出了参数优化模型。AMBROGIO等[10]、DEJARDIN等[11]提出了一种通过规划刀具路径来改善单金属板渐进回弹量的方法,并通过试验法验证了该方法的可靠性。另一些学者利用有限元方法分析了钣金成形过程中的应力应变变化规律及回弹缺陷的产生机理。ISIDORE等[12]通过有限元法研究了单板渐进成形精度随工具头直径和形状的变化规律,分析了底部的应力状态与鼓包高度的关系。史晓帆[13]应用有限元法对单板渐进成形过程中出现的回弹机理进行研究,认为回弹是由成形过程中板材的残余应力释放造成的,并提出通过局部热加工方法来减小回弹。韩飞等[14]利用有限元方法计算了多种工艺条件下的回弹量,并通过建立神经网络分析数据对单板渐进成形的回弹量进行了预测。随着双金属复合板材的广泛应用,人们发现回弹缺陷也是影响复合材料渐进成形的主要问题之一,并且由于复合板材存在结合界面,板材在成形过程中的缺陷更为复杂。而目前对双金属复合板渐进成形研究大多集中在成形机理及成形性上。HONARPISHEH等[15-16]通过有限元法分析了工艺参数对铜铝双金属复合板渐进成形中成形性能的影响,但未深入研究回弹缺陷。GHEYSARIAN等[17]研究了工具头直径、刀具轨迹等工艺参数对铜铝复合板渐进成形中成形力、厚度变化、板面质量等的影响,但没有研究板材的回弹缺陷问题。LIU等[18]通过实验研究了铜铝复合板渐进成形过程中成形力的变化及不同工艺参数对板料成形过程减薄情况的影响。上述研究的共同点之一是它们都忽略了结合界面对双金属片形成的影响,然而,复合界面对板材的内部载荷传递、局部应力和应变以及断裂机理等具有重要影响,成形过程中的界面开裂是要考虑的重要问题之一。而且在目前的双金属复合板渐进成形数值模拟研究中,复合板结合界面作为评价结合性能的关键因素被部分学者忽略[19-20],此种模拟方法存在局限性。
本文以铜铝爆炸复合板为研究对象,建立双金属复合板渐进成形有限元模型,成形过程中采用内聚力单元模拟双金属板界面情况。对渐进成形过程中多种工艺参数对回弹缺陷的影响进行了研究,并通过数学分析方法研究了不同工艺参数对鼓包高度影响的灵敏度,得到了不同工艺参数对复合板渐进成形回弹缺陷的影响规律。
1 试验研究
1.1 试验材料与设备
本文试验选用材料为350 mm×350 mm铜铝爆炸复合板,复合板材基层材料为Al-1050 和 Cu-C10100,板厚为1 mm、1.5 mm和2 mm三种,材料性能参考文献[16],如表1所示。

表1 铜铝复合板材料性能
如图1所示,本研究的成形试验均在四轴立式加工中心(HUAKEJINGLONG,HKT-1105B)上进行。试验装置主要包括工具头、夹具以及三维扫描仪。使用的工具头进给速度为1000 mm/min。使用直径分别为10 mm、16 mm和22 mm的三种工具头(Cr12MoV)来进行成形试验,并且在所有试验中均将工具头固定不旋转。成形工具头与板材之间的成形接触区用矿物油(68号)润滑,以减少摩擦并避免工具表面过度磨损。

图1 试验设备Fig.1 Test setup
1.2 试验方案
双金属复合板渐进成形的整个变形过程分为三个阶段:弹性变形阶段、弹塑性变形阶段和塑性变形阶段。在前两个阶段中,卸载后弹性变形部分会出现弹性恢复,这是引起回弹的主要原因之一,如图2所示。由于在复合板渐进成形中回弹现象受多种工艺参数影响,是一个较为复杂的问题,因此本文采用正交试验的方法来探索不同工艺参数对回弹量的影响。

图2 回弹示意图Fig.2 Schematic diagram of springback
本研究考虑了单层进给量、加工轨迹、加工深度、板厚、工具头直径、成形角六个工艺参数对复合板渐进成形回弹缺陷的影响。加工路径分为圆形单向、圆形双向和方锥形。设计了表2所示的六因素三水平正交试验,结合正交表的极差分析,对不同的工艺参数对回弹影响的敏感性进行了研究。

表2 正交试验水平表
本次试验加工参数采用正交试验表中的参数进行,加工路径获取方法为在UG软件中建立三维壳模型并使用CAM模块生成其数控机床UC代码。加工圆锥形工件时,上表面直径固定为310 mm,成形深度h及成形角α根据试验方案变化,如图3a所示。加工方锥时,边长固定为200 mm,成形深度h及成形角α根据试验方案变化,加工后部分实物图如图3b所示。

(a)圆形件实物图

(b)方形件实物图图3 成形件实物图Fig.3 Formed parts
在成形试验后,为测量其卸载回弹值,分别在夹具松开前以及夹具卸载后对成形件表面使用三维扫描仪进行表面形状成像处理,经过Geomagic Qualify软件处理得到其表面形状三维立体图,如图4所示。沿ab将截面切开,取出ab轮廓上的板材形状数据导入到CAD中获得其量化数据,比较夹具松开前后截面底部深度差即为本次试验需要的回弹量数据。
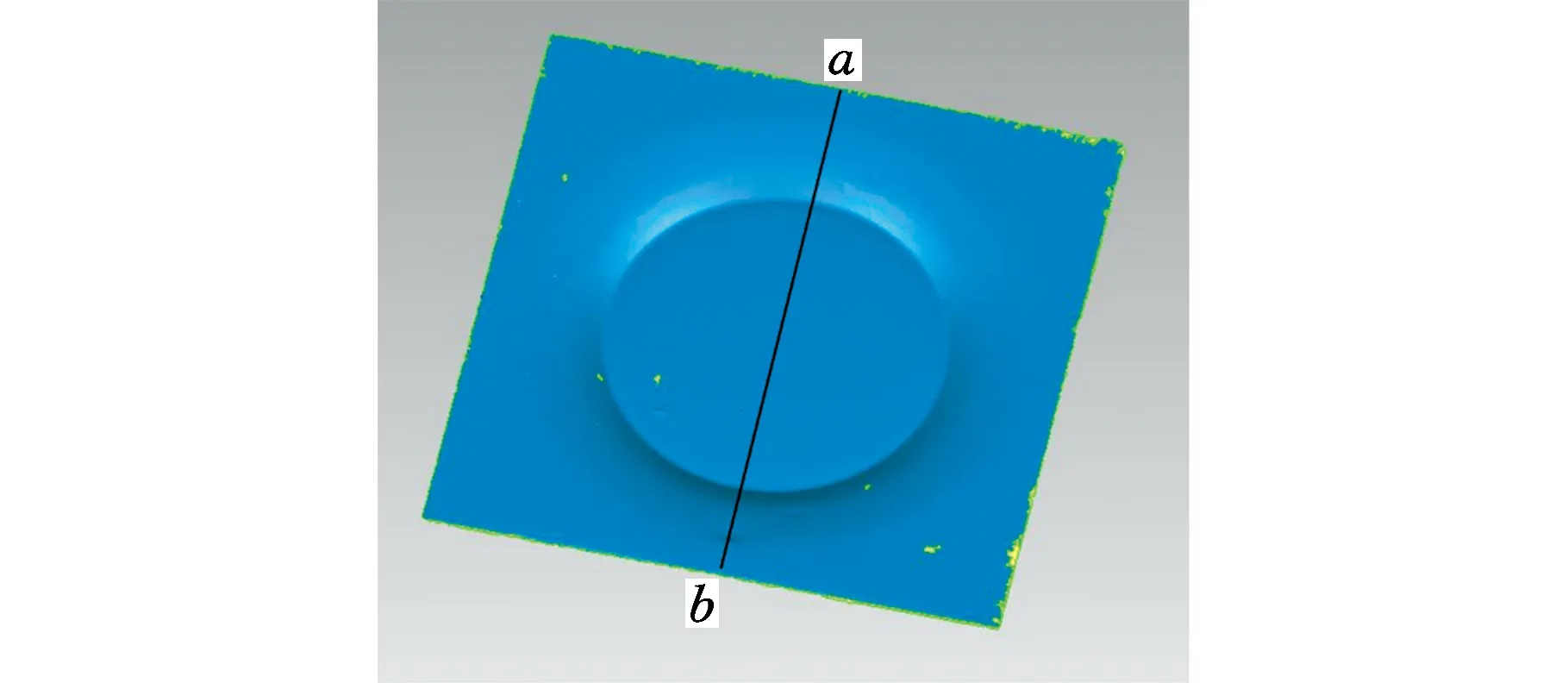
图4 成形件扫描图Fig.4 3D scan of formed part
1.3 试验结果
成形试验根据表3所示正交表依次进行,按照上述试验方案获得其回弹量。根据正交试验极差分析方法,各工艺参数不同水平各有6组数据,计算各工艺参数同一水平下的回弹量Δi均值Ki,如下式所示:
(1)
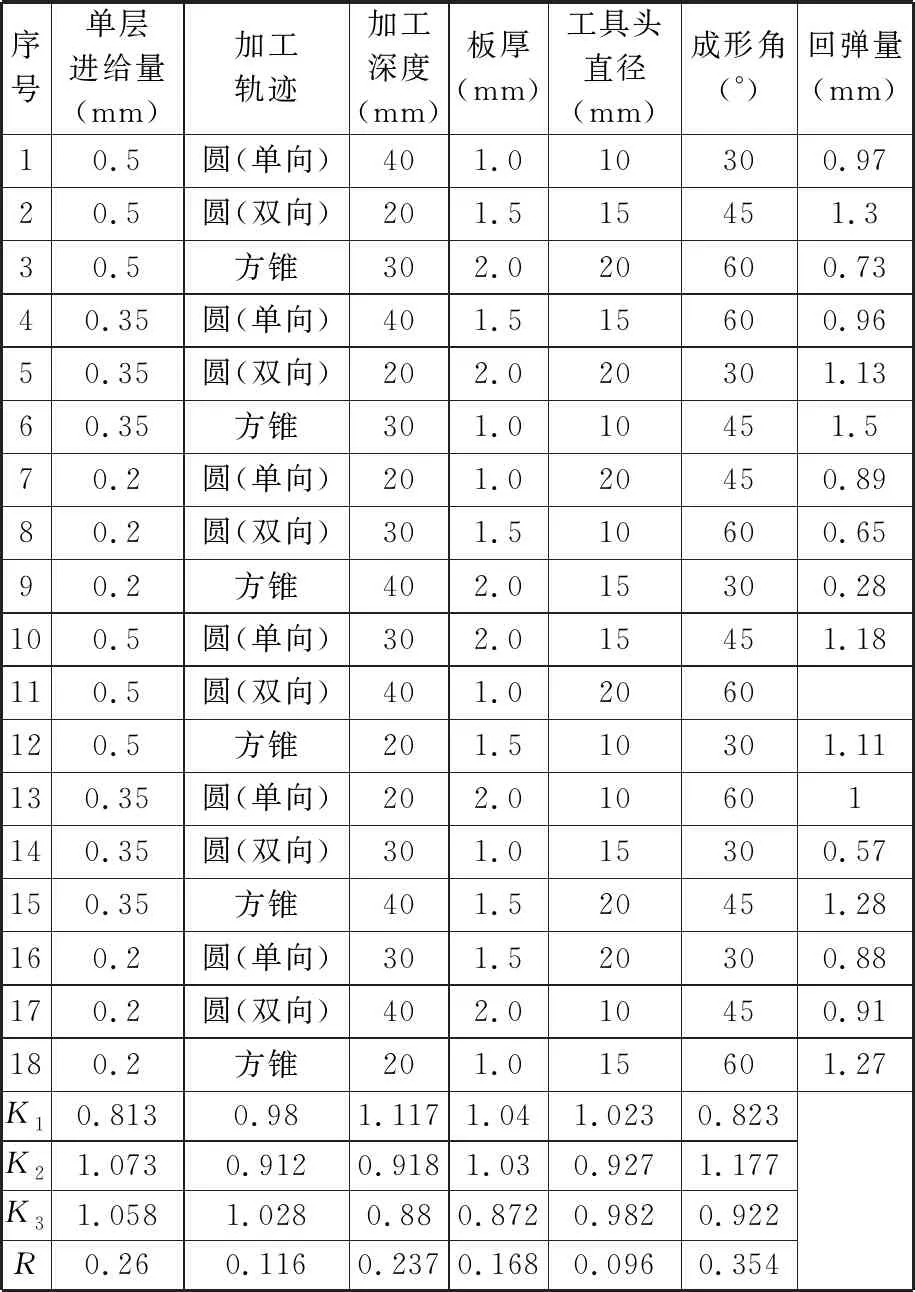
表3 工艺参数正交试验
计算出各工艺参数不同水平下的回弹量均值后,根据下式计算其极差值R:
R=max(K1,K2,K3)-min(K1,K2,K3)
(2)
正交试验中,极差值R越大,表明该工艺参数对复合板渐进成形回弹缺陷越敏感。根据正交试验极差分析结果,不同工艺参数对回弹缺陷的敏感性由大到小分别为成形角、单层进给量、加工深度、板厚、加工轨迹、工具头直径。正交试验一般反映不同工艺参数对回弹量的敏感度,不能直接体现不同工艺参数对回弹量影响的定量规律,为更加深入研究该问题,采用有限元仿真方法讨论工艺参数对回弹量的影响规律。
2 有限元模型的建立
2.1 网格参数与边界条件
本文模拟研究使用有限元软件ABAQUS建立直径为330 mm、厚度为2 mm的圆形复合板有限元模型。上下两部分分别为铜层和铝层,厚度都为0.95 mm,并采用实体单元C3DR8。中间为界面层,厚度为0.1 mm,采用内聚单元COH3D8。每部分的网格参数如表4所示,将渐进成形的工具头简化为直径为10 mm的半球,由于工具头刚度很大,在成形过程中变形极小,可忽略不计,所以将工具头设置为刚体,通过渐进成形将板料加工为图5所示上底为310 mm,下底为280 mm,高度为15 mm的圆锥形。
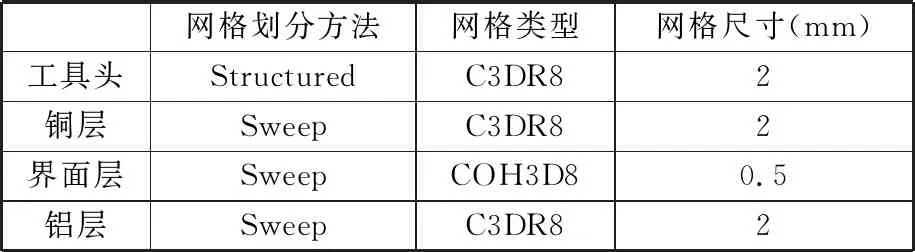
表4 铜铝复合板和工具头网格参数
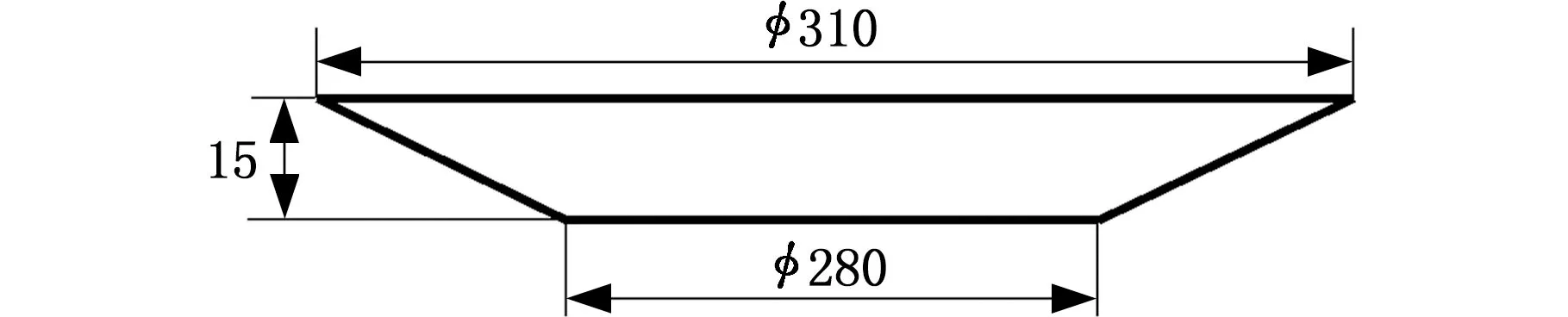
图5 零件形状Fig.5 The shape of the part
在仿真过程中选择动态显式方法进行仿真。材料变形行为设置为各向同性。工具头和板材之间的接触设置为面-面接触,摩擦因数指定为0.05。另外,为简化建模过程,将夹具固定板材简化为圆边六自由度完全固定。双金属板成形的有限元模型如图6所示。
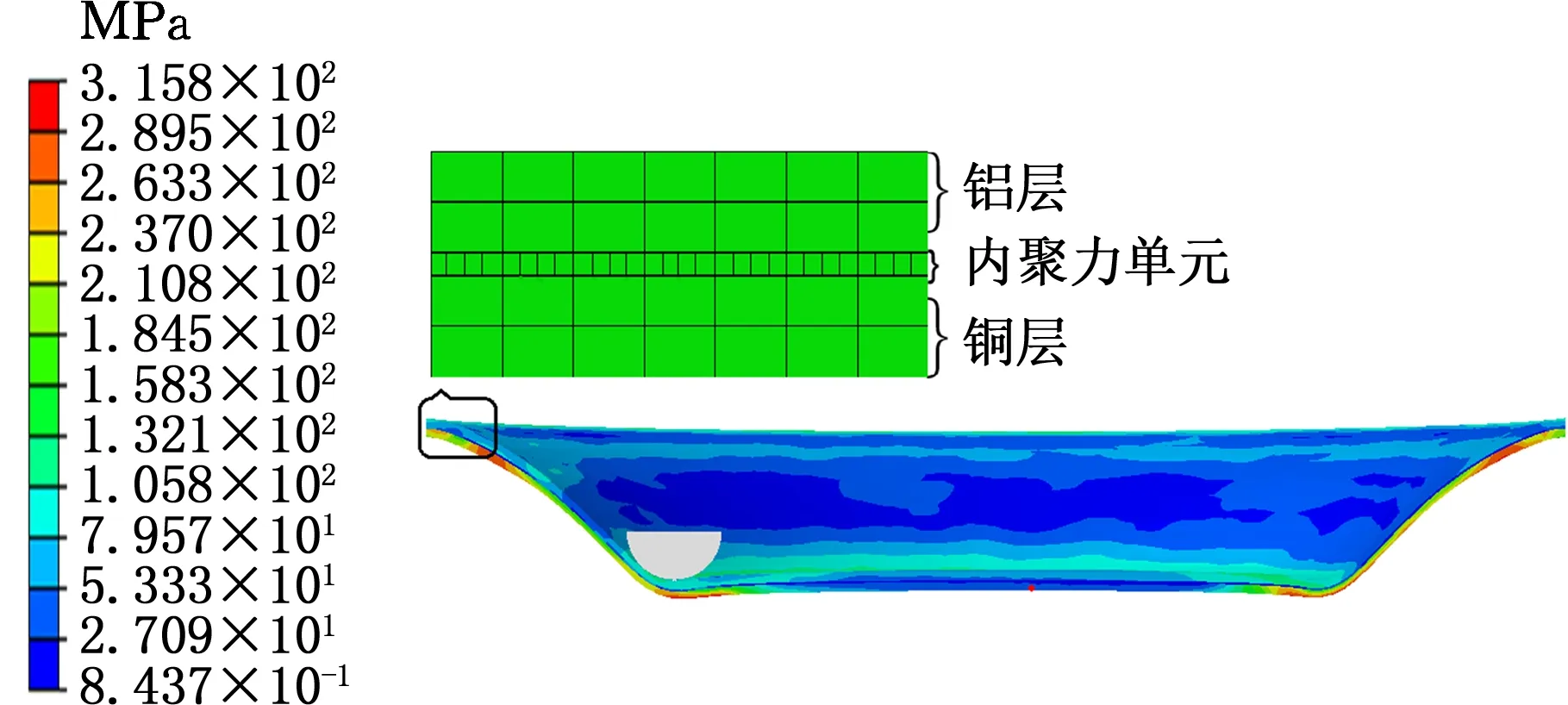
图6 铜铝复合板渐进成形有限元模型Fig.6 Finite element model of Cu-Al bimetal sheet forming
2.2 复合板界面层建模方法
在双金属复合板成形过程中,上下板的载荷主要通过界面传递。由于两种金属材料的机械性能不同,因此在成形过程中界面层附近的上下层板的局部应力和应变是不同的。当应力值超过临界值时,不同的应力状态会在界面层中引起过大的正向拉应力和切向应力,从而导致双金属复合板界面出现裂纹[21-22]。
内聚力单元由DUGDALE[23]和BARENBLATT[24]于20世纪60年代提出,可用于研究界面裂纹。经过多年发展,内聚力单元已广泛用于界面裂纹产生和扩展的数值模拟中。使用内聚力单元模拟复合界面时包括三个关键参数,分别为界面强度σ,弹性模量E和断裂能G,学者经常结合试验和模拟来确定内聚力单元的参数[25-26]。本研究的内聚力模型采用双线性本构模型,如图7所示,损伤起始准则选择二次应力损伤起始准则,损伤演化准则采用B-K准则。在外载荷作用下,内聚力单元出现损伤前,内聚力单元裂纹张力随张开位移Δ呈线性增长,此时材料处于弹性状态。当位移继续增加到Δc,张力达到最大值T时,界面开始出现损伤。随着位移的继续增大,损伤出现扩展,材料出现刚度退化,界面张力值也呈线性下降,所能承受的外载荷也逐渐减小。当位移达到Δfail时,材料刚度完全退化,界面裂纹完全拓展,材料失效。

图7 内聚力单元的双线性本构关系Fig.7 Bilinear traction-separation response of the cohesive element
本文中的内聚力模型损伤起始准则选择二次应力损伤起始准则,即
(3)
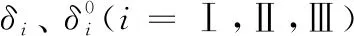
本文中的内聚力模型损伤演化准则采用B-K准则,即
(4)
GS=GⅡ+GⅢGT=GⅠ+GS
式中,Gi(i=Ⅰ,Ⅱ,Ⅲ)为应变能量释放率;GiC(i=Ⅰ,Ⅱ,Ⅲ)为界面临界能量释放率,为定义内聚力特性的量纲一参数;GC为内聚力的特征参数,为总的临界应变能量释放率。
由文献[27]可知,界面层弹性模量对界面损伤的影响很小,其值通常选取复合板基材的弹性模量。在本研究中,界面层弹性模量E取值为基材铝的弹性模量70 GPa。另外,为了获得界面层断裂能的值,本研究建立了T形剥离仿真模型。图8为T形剥离过程中内聚力单元的损伤图。根据内聚力单元的双线性本构模型,粘接元件的应力在剥离力的作用下增大,并且破坏起始标准的值逐渐增大。当破坏起始准则值达到1时,内聚力单元开始产生裂纹。随着内聚力单元的继续损坏,复合板界面刚度开始下降,刚度降低系数增大。当刚度降低系数的值达到1时,在有限元模型中会自动删除内聚力单元,界面完全破坏[28]。本文将该T形剥离模型的结果与文献[29]的实验结果进行比较,得出断裂能值为1.8 mJ/mm2时,剥离的力-位移曲线与文献[29]相符,如图9所示。当剥离臂的位移为2 mm时,剥离力达到最大值220 N,然后逐渐减小至75 N。

图8 内聚力单元损伤图Fig.8 Damage of the cohesion element
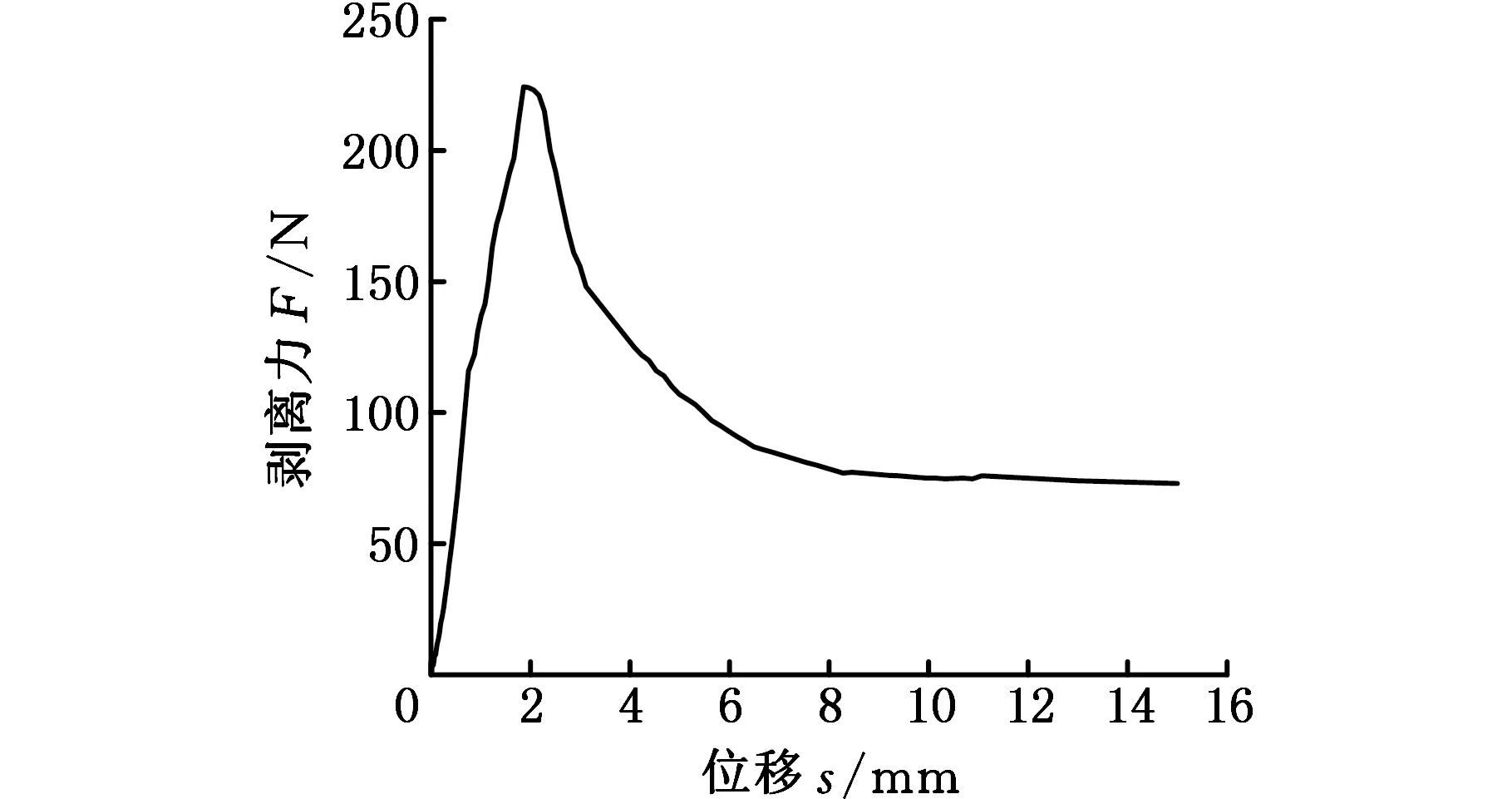
图9 T形剥离仿真结果Fig.9 The results of T-peeling simulation
为了确定双金属复合板界面粘接强度,本文在济南试金集团 200 kN电子万能试验机上进行粘接试验,如图10a所示。试验材料为铜层、铝层分别为2 mm和10 mm的爆炸复合双金属复合板,加工成形后试样如图10b所示。试验装置还包括直径为20 mm 的凹模和直径为16 mm的冲压工具头,凹模和工具头材料都为45钢。试验结果如图10c所示,断裂发生在铝层而非界面层,所以可初步得知界面结合强度大于铝层强度极限122 MPa。

(a)万能试验机 (c)试验结果 (b)试样图10 界面强度测试Fig.10 Interface strength test
此时要根据试验结果直接得到复合板界面结合强度较困难,因此,本研究假设界面强度分别为150 MPa和180 MPa,并将这些参数应用于渐进成形有限元模型中,与文献[16]中的试验结果进行比较。由图11a可以看出,当工具直径为10 mm且单层下压量为0.75 mm时,铜铝复合板在成形深度为32.59 mm时出现裂纹。在该模型中,如图11b所示,当界面强度为150 MPa时,铜铝复合板在10 mm的成形深度处出现裂纹,这与文献[16]中的试验结果不一致。当界面强度为180 MPa时,如图11c所示,在30 mm的成形深度中,铜铝复合板界面层出现裂纹,这与文献[16]中试验结果相近,误差仅为7.9%。因此,铜铝复合板的界面强度确定为180 MPa。

(a)试验结果[16]
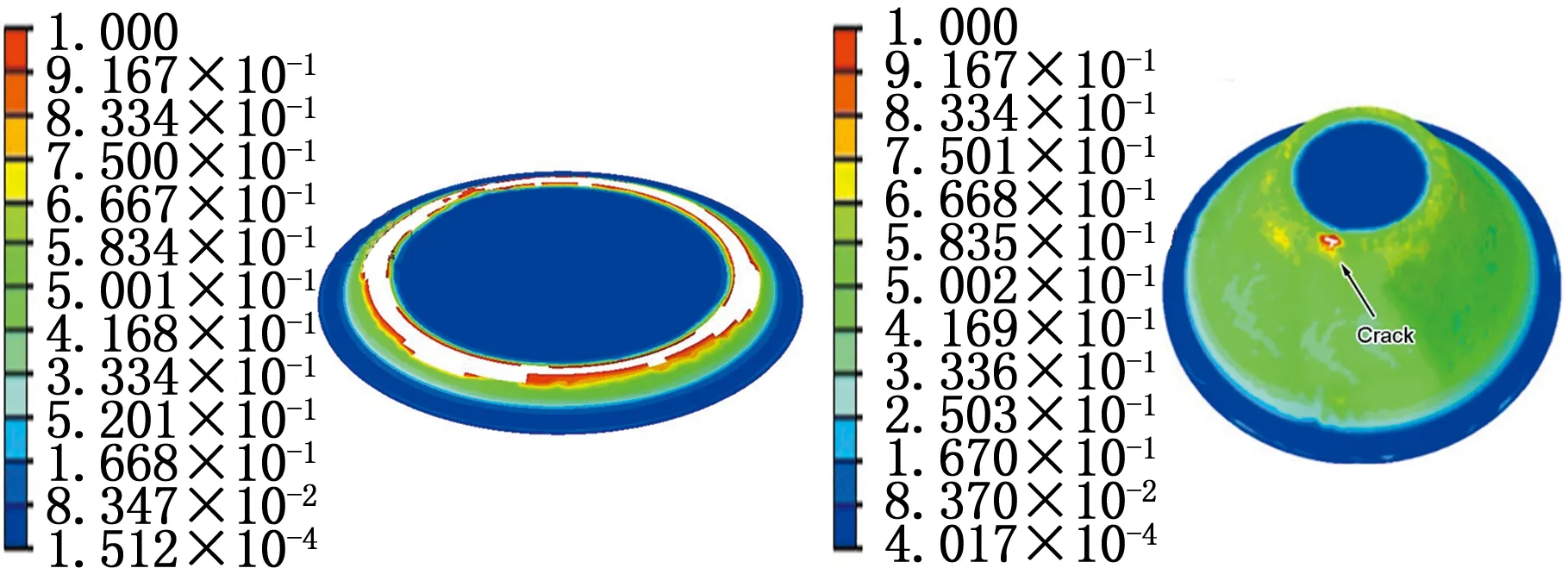
(b)σ=150 MPa (c)σ=180 MPa图11 复合板渐进成形局部开裂[16]Fig.11 Location of cracks in incremental formingof bimetal[16]
2.3 有限元仿真模型的验证
复合板渐进成形有限元仿真结束后,得到其未卸载的有限元结果,以该仿真结果为起点并去除约束,使用隐式求解器使其完成回弹过程,通过该结果提取最终回弹后的截面轮廓,回弹前后轮廓底部的差值即为板材成形回弹量。通过1.2节中的试验方法提取试验工件的轮廓图与仿真结果进行对比,当单层下压量为0.5 mm、工具头直径为10 mm、成形角为45°、板材厚度为2 mm时,经过上述方法建立的有限元模型与相同工艺参数条件下试验结果轮廓对比如图12所示,深度方向最大误差为4.6%,验证了本文有限元模型参数的合理性,可用于后续研究。
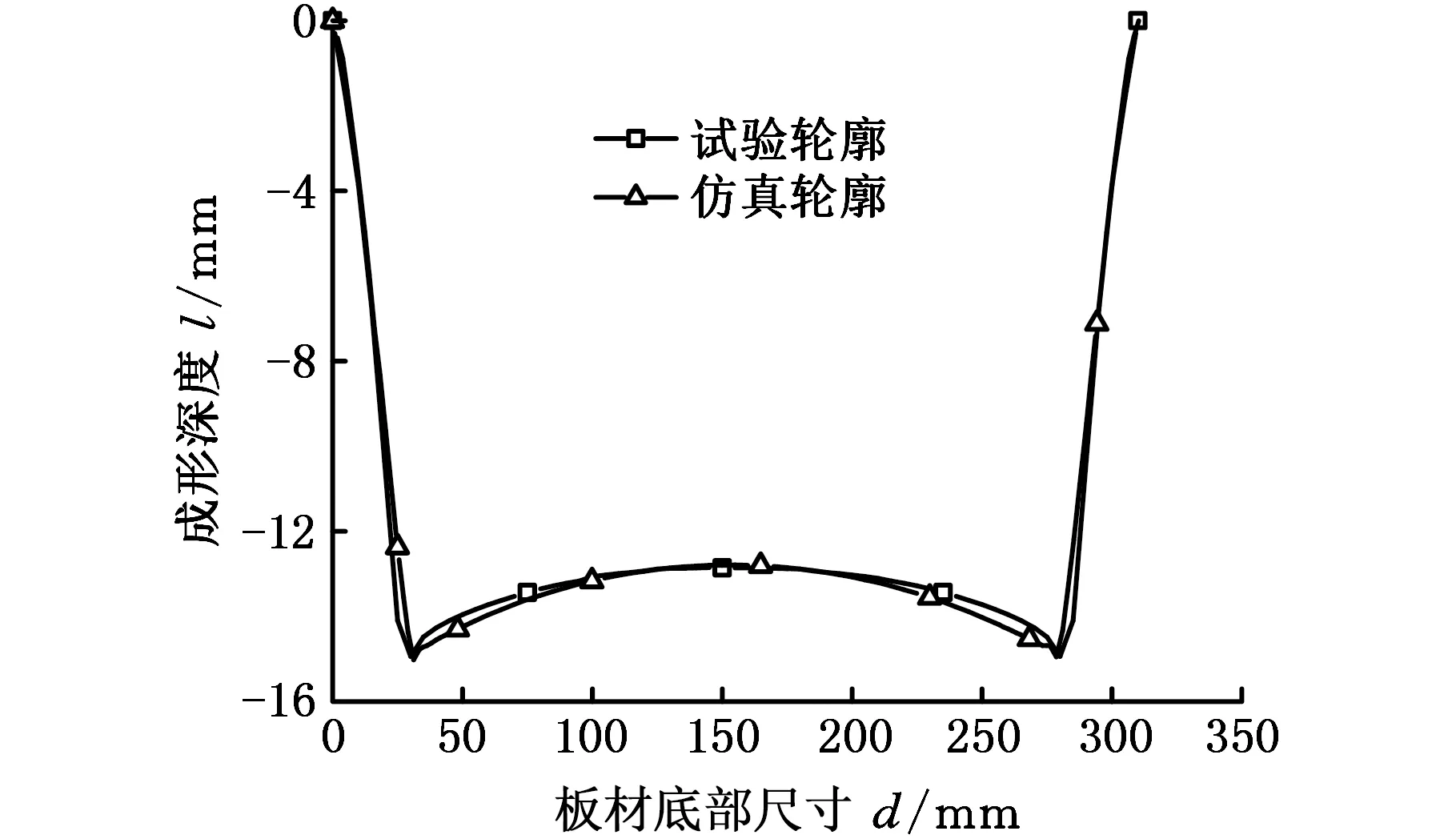
图12 有限元仿真模型验证Fig.12 Finite element model verification of thebimetal sheet
3 结果与讨论
渐进成形是一个变形逐渐积累的过程,在成形过程中,远离工具头的部分会发生局部回弹现象,本节使用有限元仿真模型,研究成形角、单层下压量、工具头直径、板厚对渐进成形过程中回弹量的影响,探究不同工艺参数对复合板渐进成形过程中回弹量的影响规律。
3.1 单层下压量对回弹量的影响
如图13所示,当每层下压量由2 mm减小至1 mm,成形深度为15 mm时,回弹量由0.4 mm减小至0.33 mm,减小了17.5%。在渐进成形中,变形区域的各种相互作用会对其他区域带来不同程度的影响。在成形过程中,变形区域周围的材料产生的变形中存在大量弹性变形的成分,较小的单层下压量可使材料的塑性变形更加充分,减小弹性变形的比例,可使加工过程中的回弹量减小。
不同单层下压量对板材等效塑性应变的影响有限元分析结果如图14所示,可以发现,当单层下压量为1 mm时,成形区等效塑性应变最大为1.699,当单层下压量为2 mm时,成形区等效塑性应变值最小,为1.005,这意味着较小的单层下压量使得板材塑性变形更加充分,回弹量较小。在渐进成形中不同工艺参数对回弹量的影响主要体现在等效塑性应变的不同上,此处以单层下压量为例揭示工艺参数对成形回弹机理的影响。
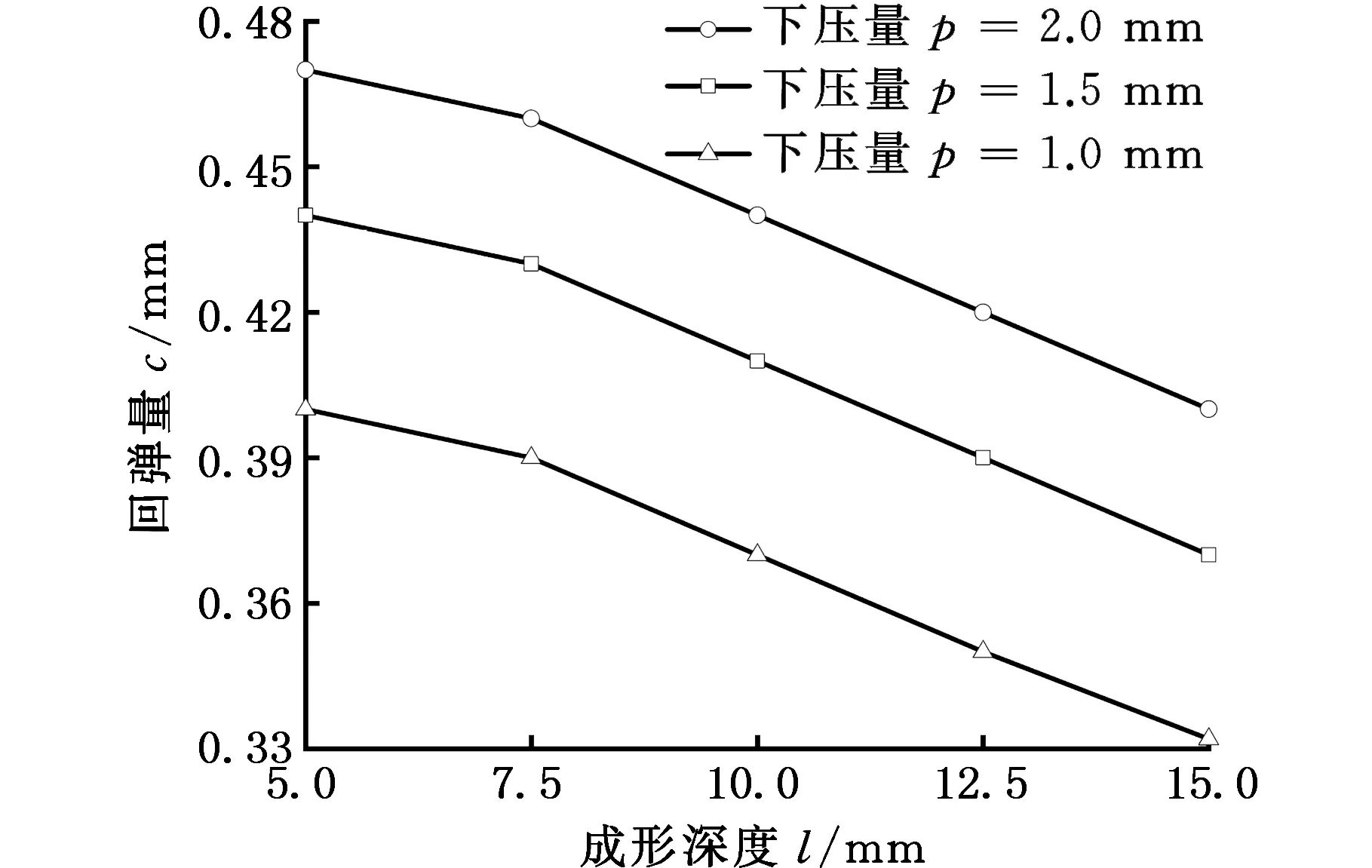
图13 下压量对回弹量的影响Fig.13 The effect of step-down size on springback
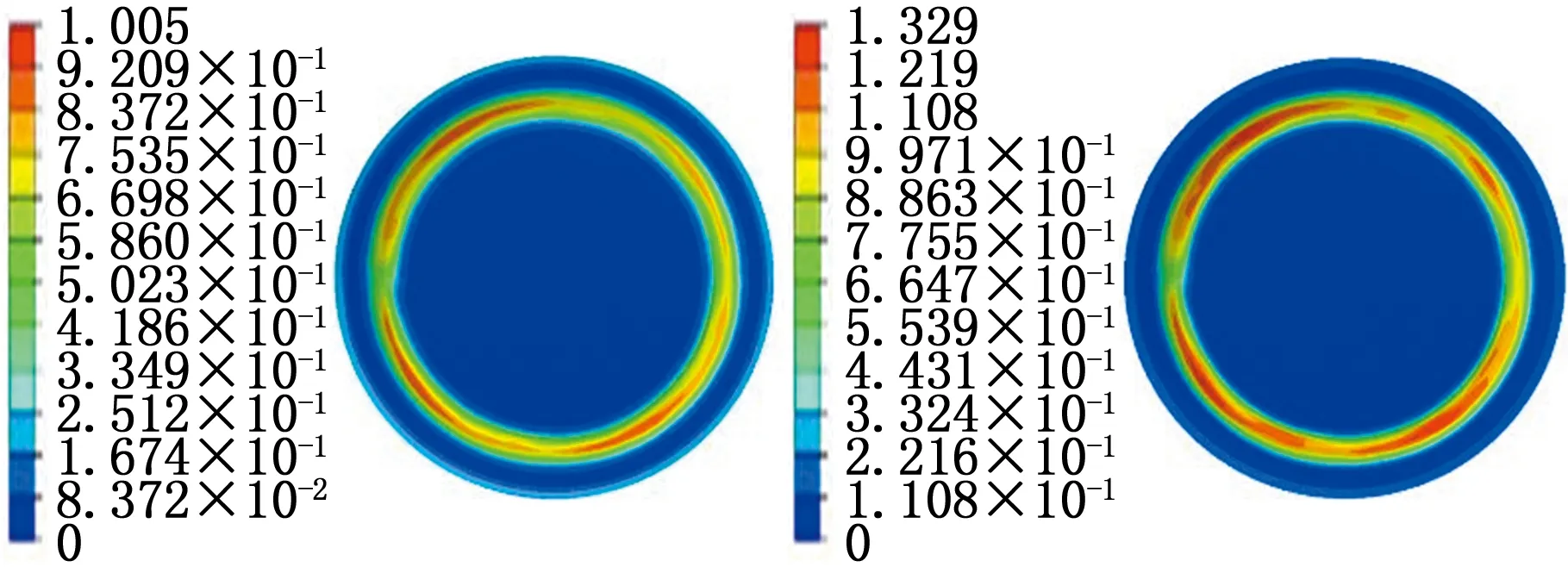
(a)单层下压量p=2 mm (b)单层下压量p=1.5 mm

(c)单层下压量p=1 mm图14 单层下压量对板材等效塑性应变的影响Fig.14 The effect of step-down size on equivalent plastic strain
3.2 成形角对回弹量的影响
如图15所示,成形深度从5 mm增大到15 mm,不同成形角下的回弹量均表现为减小趋势,这是由于随着成形深度增大,板材塑性变形更加充分,弹性恢复变小,所以回弹量逐渐减小。当成形角从30°增大至60°,成形深度为15 mm时,回弹量从0.42 mm减小至0.33 mm,减小了21%。从力学角度分析,在渐进成形过程中,成形角的增大会导致更大的塑性变形量和更大的塑性变形区,减小弹性变形对成形的影响。而当成形角较小时,塑性变形在总变形中所占比例相对较小,增大了弹性变形对精度的影响,此外,受几何关系的限制,在成形不同成形角的零件时,成形力在Z方向的分量对制件成形部分边缘位置的弯矩是不同的,在成形深度相同的情况下,成形角越小,制件已成形区域所承受的弯矩越大,这也造成制件上出现了部分的弯曲性回弹,因此,在渐进成形过程中,大成形角有利于减小成形的回弹缺陷。
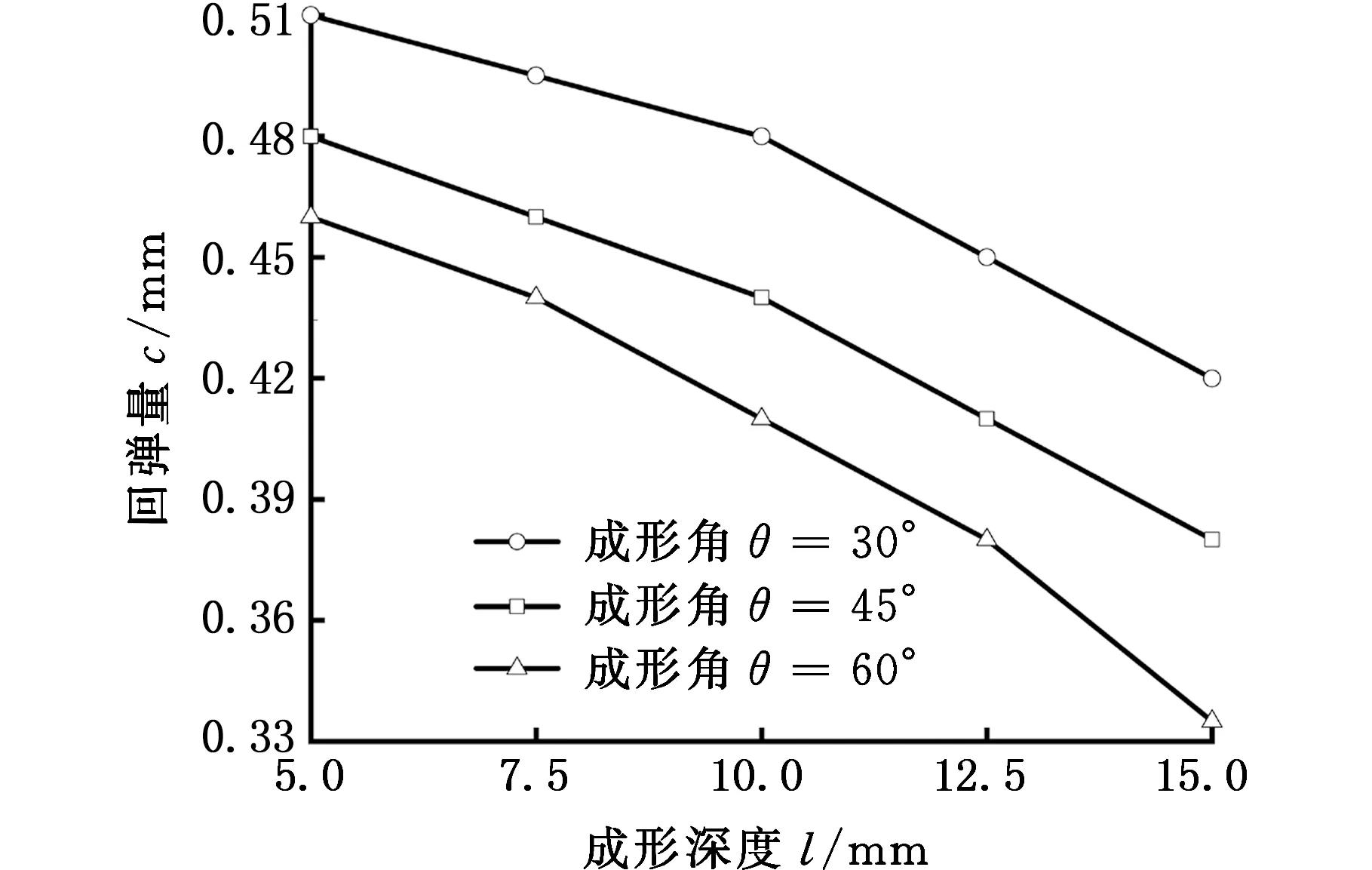
图15 成形角对回弹量的影响Fig.15 The effect of forming angle on springback
3.3 工具头直径对回弹量的影响
如图16所示,当工具头直径由10 mm增至20 mm,成形深度为15 mm时,回弹量由0.39 mm增至0.48 mm,增大了18.7%。这是因为在单层下压量和成形角一定的情况下,工具头直径较大时,工具头与板材表面接触面积将增大,这会导致弹性变形区较大,而弹性变形的恢复是导致回弹缺陷的主要原因,因此应选择较小的工具头直径来减小回弹。尽管较小的工具头直径可以减小制件的回弹量,但结合文献分析,当成形工具头较小时会导致板材底部鼓包缺陷加重。因此,在成形时必须要综合考虑各方面因素,不能仅仅依靠减小成形工具头直径的方法来减小回弹,必须考虑到成形工具头的变化对其他成形缺陷带来的影响。

图16 工具头直径对回弹量的影响Fig.16 The effect of tool diameter on springback
3.4 板厚对回弹量的影响
如图17所示,板厚由1 mm增大到2 mm,成形深度为15 mm时,回弹量由0.35 mm增大到0.42 mm,增大了17%。在板材渐进成形过程中,板厚的变化影响着上下表面材料的应力差。在本次加工中,加工面为铝面受压应力,下表面为铜面受拉应力,使板材处于弯曲应力状态。材料性能不同使得上下表面塑性变形情况不同,板厚增大时,会使弯曲应力状态加剧,使板材加工过程中除了弹性恢复外,还有部分弯曲变形恢复导致的回弹,所以板厚增大会加剧回弹现象。在实际应用中,板厚受多方面因素影响,如板材强度、质量等,因此在选择板厚时,在满足使用需求的情况下应选择厚度较小的板材来减少成形过程中的回弹缺陷。
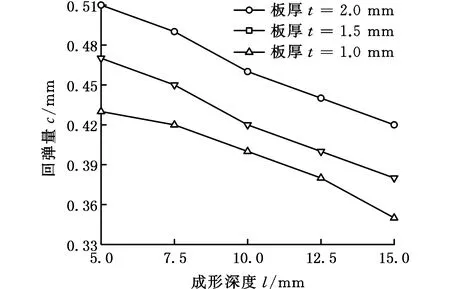
图17 板厚对回弹量的影响Fig.17 The effect of sheet thickness on springback
3.5 复合板基材板厚对回弹量的影响
复合板不同基材占比对复合板渐进成形回弹的影响如图18所示,横坐标为铜层占复合板总板厚的比例。研究了总板厚2 mm,铜铝比例分别为0∶1、1∶2、1∶1、2∶1、1∶0五种情况下复合板回弹量变化情况。结果显示,板材回弹量随铜层占比从0增加到100时,复合板的回弹量增大了20%。这主要是因为铜的屈服强度比铝的屈服强度大,成形后回弹量也比铝的回弹量大,铜铝复合板在成形后铜的弹性恢复阶段,铝材会对铜材的弹性恢复有一定抑制作用。因此铜铝复合板不但可以减少铜材的消耗,还会增强板材的塑性成形能力。

图18 铜层占比对回弹量的影响Fig.18 The effect of the percentage of copper layer on springback
4 结论
本研究综合运用试验和有限元法研究了不同工艺参数对铜铝复合板材渐进成形回弹缺陷的影响。在有限元模型中,使用内聚力单元模拟复合板界面层来代替传统的绑定约束。得到的主要结论如下:
(1)本文建立了一个包括工具头、铜铝复合板和复合板界面层的三维模型,模拟结果与试验结果误差仅为7.9%。使用该模型讨论了不同工艺参数对回弹缺陷的影响。
(2)研究结果表明,不同工艺参数对复合板渐进成形回弹缺陷的敏感性大小顺序为:成形角、单层进给量、加工深度、板厚、加工轨迹、工具头直径。另外,复合板渐进成形回弹量与基材材料属性密切相关,随着铜层比例增加,回弹量增大20%。
(3)单因素分析发现,成形角从30°增大至60°时,回弹量下降21%;单层下压量由1 mm增大至2 mm时,回弹量增大17.5%;板厚由1 mm增大到2 mm时,回弹量增大17%;工具头直径由10 mm增大至20 mm时,回弹量增加18.7%。

