基于相变与收缩耦合的1Cr12焊缝冷却动态力学行为
许 谦 胡广旭 董志波 任新星 方洪渊
1.中国科学院新疆天文台,乌鲁木齐,8300012.中国科学院射电天文重点实验室,乌鲁木齐,830011 3.哈尔滨商业大学轻工学院,哈尔滨,150028 4.哈尔滨工业大学先进焊接与连接国家重点实验室,哈尔滨,150001
0 引言
焊接是钢结构制造最常用的工艺方法之一,具有成本低、效率高、工艺灵活等优势。然而,焊缝冷却过程中局部动态力学行为受形貌尺寸、降温梯度以及材料演变等多种复杂因素影响,易于产生内部微观缺陷,因此焊缝及附近区域往往也是结构承载的危险点。1Cr12钢为马氏体不锈钢,常用于高应力耐腐蚀载荷结构(如汽轮机叶片)[1],研究1Cr12钢焊缝冷却过程动态力学行为,有助于进一步深入地分析1Cr12结构在高应力负载作用下的力学响应,对评估1Cr12结构疲劳寿命预测具有重要意义。
近年来,研究者针对HY100、P91、P92等高强钢的焊接固态相变影响展开相关研究,建立了热-冶金-力耦合材料本构模型,分析了相变过程对焊接纵向残余应力的影响[2-5],但对相变过程中焊缝冷却动态力学行为的分析较少。本文针对1Cr12材料,在前人基础上,全面考虑马氏体相变体积应变、过冷奥氏体与马氏体两相体积不溶性引起的混合相力学性能、相变塑性以及混合硬化的影响,建立相变与冷却收缩耦合的数值模型,分析模型各要素对1Cr12钢焊缝冷却动态力学行为的影响。
1 1Cr12焊接试验
本研究所用材料1Cr12钢的主要成分见表1。

表1 1Cr12钢主要成分
对1Cr12钢平板进行TIG(tungsten inert gas)重熔试验,焊接电流为130 A,电压为12 V,焊接速度为200 mm/min。平板规格及焊接工艺与模拟时完全相同。焊接完成后,采用盲孔法对焊后残余应力进行测试,应变采集设备为CM-1J-20静态电阻应变仪,图1所示为试验件与测量设备。

(a)三向电阻应变片

(b)静态电阻应变仪图1 应力测量试验设备Fig.1 Stress measurement testing equipment
2 焊缝冷却收缩与相变数值模型
焊缝金属组织与力学状态主要取决于冷却凝固阶段的相变与动态力学演变过程。首先,当仅从热-力学方面考虑时,焊缝冷却收缩时,受到已冷却金属的拘束,在焊缝纵向处于受拉状态。高温时材料屈服强度较低,温度降速快,纵向收缩热应变大,产生拉伸屈服;随着温度降低,材料屈服强度逐渐向室温值恢复,降温梯度变小,收缩热应变量减小,此时一般不发生屈服,焊缝纵向处于弹性受拉状态,并随着温度的降低,拉应力逐渐增大,最终保留在焊缝内部,形成焊接残余拉应力。然而,上述过程未考虑降温过程中固态相变对焊缝动态力学行为的影响。1Cr12钢降温至200℃左右时开始发生马氏体相变,产生相变体积膨胀,与焊缝降温收缩共同作用,影响此阶段焊缝受力状态;同时,马氏体相变过程中,存在马氏体与奥氏体两相混合的动态组织阶段,此时瞬态材料力学性能与各相体积分数相关,进一步影响焊缝力学行为;此外,焊缝相变时产生相变塑性应变与拉伸塑性应变共同使材料产生硬化,影响进一步的力学状态。
2.1 相变体积应变模型
奥氏体相变采用Kamamoto模型[6]描述,其数学表达式如下:
(1)
式中,T为当前温度;Ac1、Ac3分别为奥氏体转变开始温度和结束温度;f为温度T时奥氏体转变量;f0为转变结束时奥氏体转变总量;p为奥氏体体积分数;k、n分别为由相变类型和材料组分决定的相变常数(表2)。

表2 Kamamoto模型参数
马氏体转变属于非扩散型相变,常用K-M(Koistinen-Marburger)方程[7]来描述,数学表达式如下:
p=1-exp(-μ(vT)(Ms-T))
(2)
式中,Ms为马氏体相变开始温度;μ为与成分有关的常数;vT为冷却速度。
通过拟合式(2)曲线可以确定μ的大小,见表3。

表3 K-M方程参数
基于相变体积分数计算相变应变,公式如下:
Δε′vol=εvolΔfB
(3)
式中,Δε′vol为相变应变增量;ΔfB为单位时间增量内的相变转变量;εvol为新相完全转变时的相变应变。
由于相变应变增量与热应变增量Δεthe具有相同的形式,故将相变应变增量Δε′vol加入到热应变增量Δεt中,完成固态相变效应中体积变化的表征,计算公式如下:
Δεt=Δεthe+Δε′vol=αΔT+εvolΔfB=α′ΔT
(4)
(5)

2.2 混合相力学性能模型
目前,P91钢采用线性混合法则[3]描述其混合相力学性能,然而马氏体与奥氏体的质量热容相差较大,产生体积不溶性,且低强度相易产生微观塑性应变[8],因此线性混合法则难以满足条件。本文应用等塑性应变假设[9],认为混合相中各组分的塑性应变εpq与材料的宏观塑性应变相等,即
Ep=εpq
(6)
式中,Ep为宏观塑性应变;q为混合相中各相序数。
当采用混合法则对材料的力学行为进行描述时,宏观应力可以表述为
∑S=∑f(ξq)σsq
(7)
式中,ξq为q相的体积分数;σsq为各相应力;f(ξq)为ξq的归一化函数,即∑f(ξq)=1。
当混合相材料中只存在两相时,式(7)可以简化为
∑S=f(ξ1)σs1+(1-f(ξ1))σs2
(8)
本研究采用热模拟试验机测量了在相变温度区间内(即不同马氏体体积分数下)1Cr12的屈服强度,如图2所示。同时,图2中给出了使用不同归一化函数计算得到的混合相屈服强度曲线。对比试验结果可知,采用下式的归一化函数能够更准确地描述马氏体-奥氏体混合相组织的力学性能:
f(ξ1)=ξ3/2
(9)
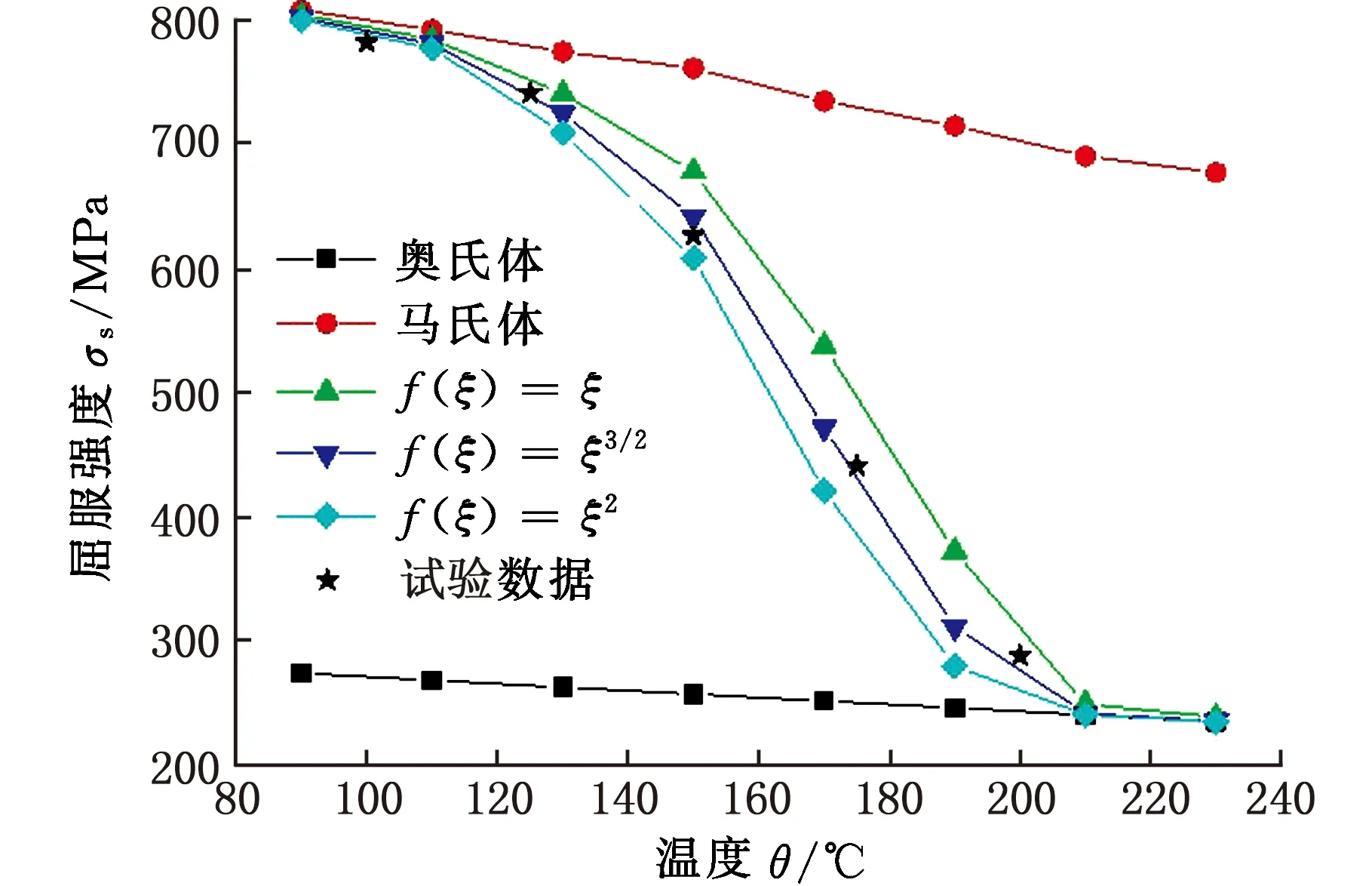
图2 混合相屈服强度对比Fig.2 Comparison of yield strength for mixed phase
2.3 混合硬化模型
混合硬化模型是在等向硬化模型[10]和随动硬化模型[11]基础上加权计算得到的,其加载函数如下:
f=f*(sij-bij)-σy=0
(10)
对等向硬化和随动硬化模型分别作出相应的修正:
(11)
(12)
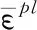
根据高温拉伸试验测定的母相在不同温度(20 ℃、100 ℃、200 ℃、400 ℃、600 ℃、800 ℃)下的真实应力-应变数据,可以求得等向硬化参数m、n和塑性模量Ep,见图3。
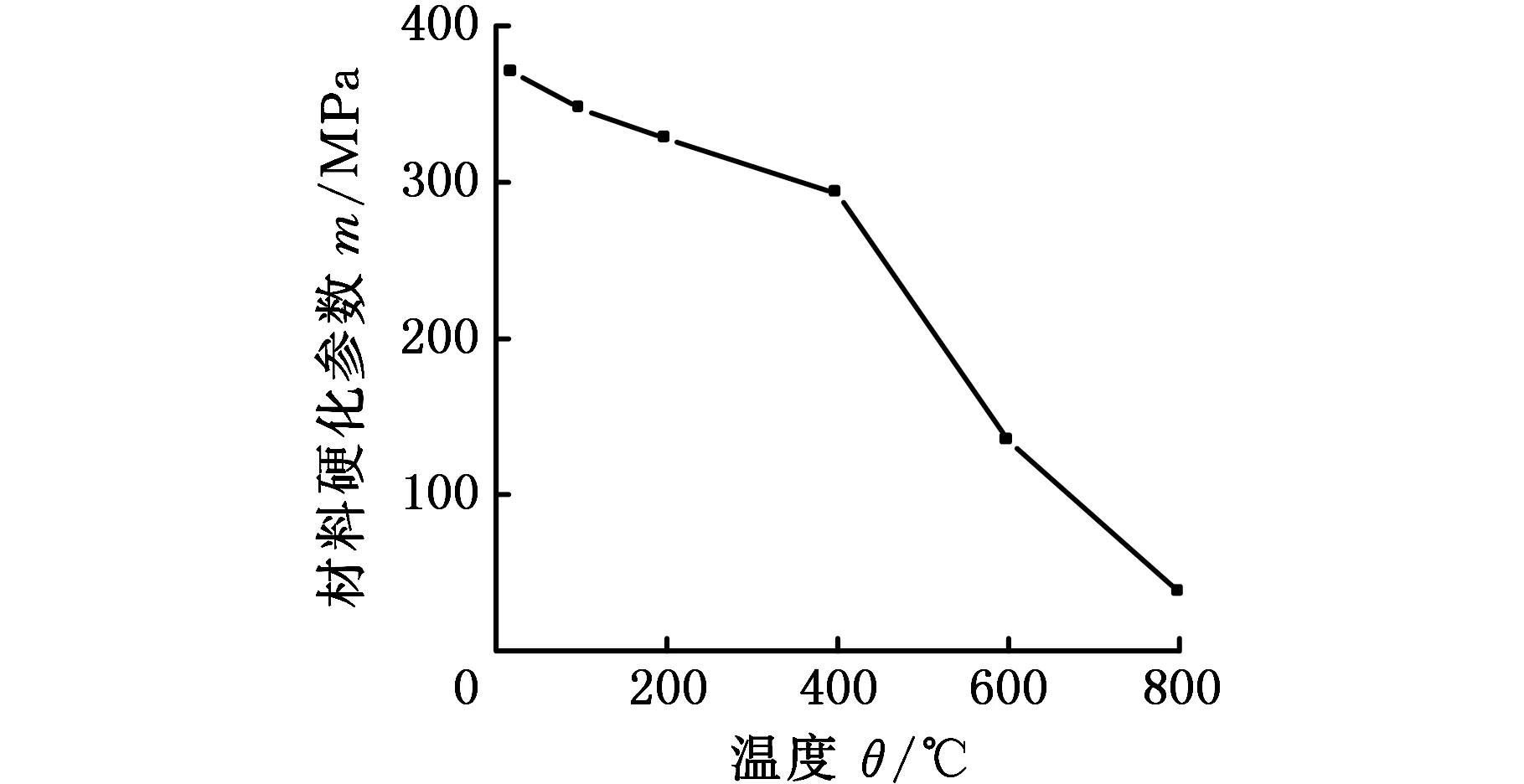
(a)m值
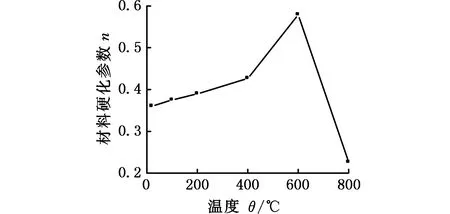
(b)n值

(c)Ep值图3 材料常数曲线Fig.3 Curves for material constrant
2.4 相变塑性模型
焊接冷却过程中,过冷奥氏体发生马氏体转变时,低强度的奥氏体相在内应力和收缩拉应力的共同作用下会产生相变塑性应变。基于Greenwood-Johnson机制对相变诱导塑性应变描述如下[12]:
(13)

2.5 相变与收缩耦合集成模型
开展焊接热-力耦合数值模拟有限元计算时,其热-力总体控制方程如下:
热分析控制方程
(14)
力学分析控制方程
k(T,u,t)u=F
(15)
刚度矩阵中的应变-位移关系
ε=βu
(16)
应力-应变关系
σ=Lε
(17)
式中,Qp为塑性应变能;Q为系统输入热量;C(T)为随温度变化的质量热容;k(T)为随温度变化的传热系数;k(T,u,t)为随温度、位移以及时间变化的刚度;F为系统所受外力;ε为系统应变;σ为系统应力;L为弹塑性应力-应变增量关系系数;β为应变-位移关系系数。
在焊接热-力耦合过程中,由于剧烈热胀冷缩过程产生塑性应变,因此采用增量理论进行计算,式(17)转变为
Δσ=LΔε
(18)
式中,Δε为系统应变增量;Δσ为系统应力增量。
当不考虑材料硬化时,本研究采用Mises屈服准则判断材料是否处于弹塑性阶段的条件为
(19)
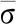
在有限元分析中,常需根据应变增量计算应力增量,热-力耦合应变增量如下:
Δε=Δεe+Δεp+Δεth
(20)
式中,Δεe为弹性应变增量;Δεp为塑性应变增量;Δεth为热应变增量。
在上述热弹塑性有限元分析基础上,考虑相变体积应变与热应变作用类型相同,通过式(5)中的等效热膨胀系数将相变体积应变集成至式(20)中。考虑混合相力学性能时,主要通过式(9)获得材料随温度变化的屈服强度,并将其作为式(19)中σy的初始值σs,进一步考虑混合硬化时,用式(10)替代式(19),并利用式(11)混合强化模型计算式中的σy,实现混合硬化模型集成。将相变塑性模型中式(13)集成至式(20)的塑性应变增量Δεp项内,最终完成相变与冷却收缩耦合的热-力学建模。
3 试验与模拟结果对比
3.1 试验件有限元模型
本研究采用试验件模型的一半进行建模分析。建立模型位移约束条件时,在保证模型不发生刚性移动的前提下不增加额外位移约束,其中在对称面上设置对称约束,即限制对称面节点x方向上的自由度;热学边界条件主要为工件表面与环境的换热条件,主要包括对流与辐射边界条件。为了分析相变体积应变、混合相力学性能、相变塑性等因素的影响,建立了表4所示的6种计算模型。

表4 不同计算案例
3.2 结果对比
由图4中案例1与案例6条件下的纵向残余应力沿工件横向距离分布曲线可知,案例1不考虑固态相变效应时,其峰值应力为570 MPa拉应力,远离焊缝纵向应力逐渐减小并变为压应力。而案例6考虑固态相变效应后,焊缝相变区纵向应力值为-143 MPa,峰值应力出现在相变区域与母材的交界处,为613 MPa。案例6的计算结果与实验测量结果基本一致,说明考虑固态相变更符合实际结果。

图4 纵向残余应力对比Fig.4 Longitude residual stresses comparison
3.3 焊缝冷却动态力学行为分析
3.3.1相变体积应变影响
由图5所示焊缝纵向应力随热循环变化曲线可知,在降温阶段,案例1与案例2曲线主要差异在降温阶段的马氏体相变区。案例2考虑相变体积应变时在相变过程中纵向拉应力值逐渐减小,直至趋近于0。这说明焊缝相变体积膨胀引起的金属受压作用与冷却收缩引起的金属受拉作用相互抵消。同时,在马氏体相变温度区间内,开始时相变速度较快,随后逐渐缓慢。相应地,案例2曲线纵向拉应力值下降趋势也与相变速度变化相符。由图6所示的纵向残余应力沿横向距离变化的曲线可知,在相变区范围内,距离焊缝越近,金属相变体积分数越大,其体积膨胀作用越明显,纵向残余拉应力值越小。
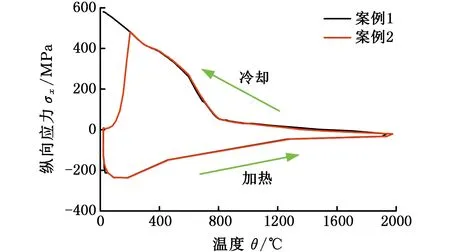
图5 焊缝纵向应力随热循环的演变(案例1,2)Fig.5 The bead longitude stress along with thermal cycle(case1,2)
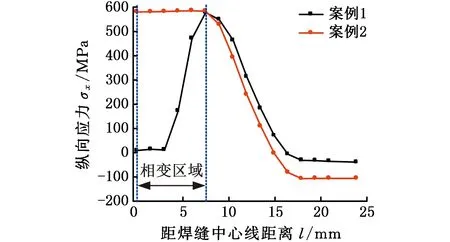
图6 沿横向分布的纵向残余应力(案例1,2)Fig.6 Longitude residual stress along transverse(case1,2)
3.3.2混合相力学性能影响
图7所示分别为案例3与案例2工况条件下纵向应力随温度变化曲线。高温区初始降温阶段,案例3与案例2金属组织均为高温奥氏体,此时两者材料屈服强度一致,但受周围邻近区域影响(考虑混合相力学性能影响时奥氏体周围邻近点的材料屈服强度较小),案例3工况下纵向残余应力比案例2工况下纵向残余应力略小一些。温度进一步降至马氏体相变区时,案例2工况下焊缝金属转变为马氏体,其材料屈服强度较案例3工况下焊缝金属材料屈服强度高,因此两者条件下焊缝纵向残余应力值的差异逐渐增大。在低温区焊缝附近降温速度变缓,材料不易屈服。因此,案例2与案例3工况下马氏体转变的膨胀作用对焊缝收缩拉应力的抵消幅度几乎一致。然而,由于案例3工况下整个降温阶段残余拉应力值较低,因此体积膨胀使焊缝最终处于压应力状态,应力值约为-220 MPa。此时,处于中心相变区的焊缝纵向均为压应力状态,如图8所示。
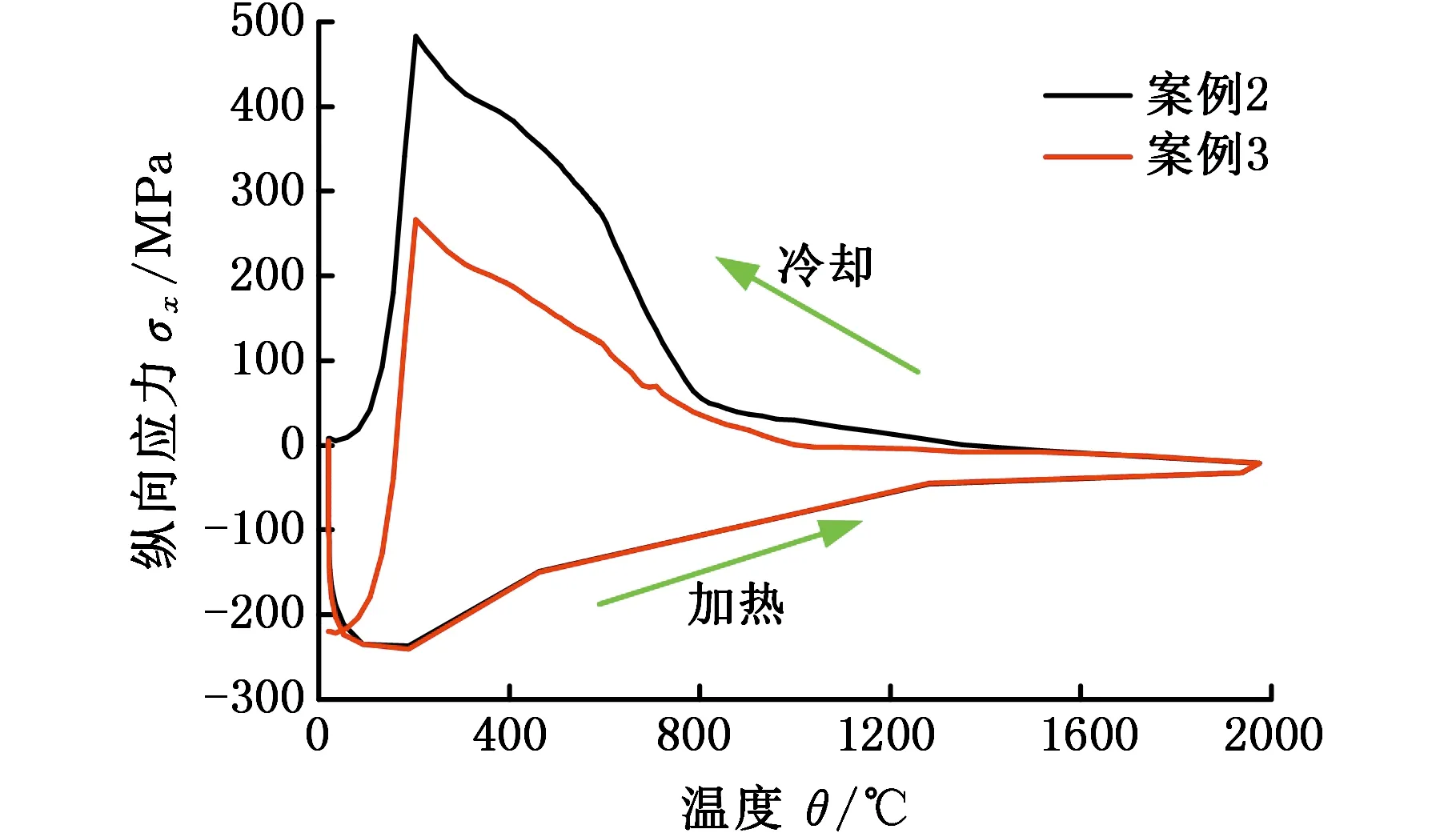
图7 焊缝纵向应力随热循环的演变(案例2,3)Fig.7 The bead longitude stress along with thermal cycle(case2,3)

图8 沿横向分布的纵向残余应力(案例2,3)Fig.8 Longitude residual stress along transverse(case2,3)
3.3.3相变塑性的影响

图9 焊缝纵向应力随热循环的演变(案例2,4)Fig.9 The bead longitude stress along with thermal cycle(case2,4)
如图9所示,考虑相变塑性影响时(案例4曲线),仅在材料冷却至马氏体相变温度区间时开始有小幅度影响。由式(13)可知,马氏体相变开始过程中在焊缝区产生拉伸应力,此部分应变与相变体积膨胀应变共同抵消冷却收缩产生的拉应力,从而增大了焊缝区受压的幅度,即案例4考虑相变塑性使焊缝在案例2模型基础上进一步受压,最终处于压应力状态。进一步,当焊缝转变为压应力状态时,尽管相变塑性将产生压缩塑性应变,但此时马氏体相变已接近尾声,因此此部分压缩应力状态下的相变塑性可以忽略不计。最终相变塑性使焊缝相变区应力转变为压应力状态,如图10所示,其应力值约为-50 MPa。

图10 沿横向分布的纵向残余应力(案例2,4)Fig.10 Longitude residual stress along transverse(case2,4)
3.3.4混合强化影响

图11 焊缝纵向应力随热循环的演变(案例2,5)Fig.11 The bead longitude stress along with thermal cycle(case2,5)
如图11所示, 案例5条件下材料在马氏体相变温度以上的温度区间降温时,由于考虑混合强化作用,材料屈服强度随温度的降低而增大的幅度更大,因此其降温过程的动态拉应力值较案例2不考虑混合强化时更大,而且两者差值不断增大。当降温至马氏体相变温度区间时, 案例5条件下金属纵向拉应力与案例2条件下的纵向拉应力差值达100 MPa,说明混合强化作用在马氏体相变区以上的冷却阶段对焊缝的纵向拉应力影响较大。而最终两者应力差值仍为100MPa左右。进一步降温到马氏体相变区温度区间以内时,两者焊缝降温梯度变缓,材料不易屈服,此时两者焊缝动态拉应力在相变体积应变影响下开始减小,且减小趋势几乎一致,此时混合强化作用几乎可以忽略,因此案例2和案例5条件下焊缝最终纵向拉应力差值仍为10 MPa左右,说明混合强化作用使焊缝残余应力增大约100 MPa,如图12所示。

图12 沿横向分布的纵向残余应力(案例2,5)Fig.12 Longitude residual stress along transverse(case2,5)
由上述分析可知,1Cr12焊缝相变体积膨胀使焊缝受压,这种压缩作用可以抵消焊缝冷却收缩产生的拉伸作用,由于焊缝冷却收缩所受瞬态拉伸作用是导致焊缝内部裂纹缺陷的要素之一,因此1Cr12马氏体相变在力学上可以起到抑制焊缝开裂的作用;其次,从混合相力学性能角度分析,材料在高温奥氏体区降温受拉时,由于屈服强度较低,易于产生较大塑性变形,金属组织处于塑性流动状态,增大了焊缝产生内部缺陷的概率,建模时应考虑混合相力学性能的影响;另外,在高于马氏体相变温区的降温过程中,混合强化作用使材料降温时屈服强度的增幅提高,从而增加了初始降温阶段的动态拉应力值,同时材料硬化后使塑性储能减少,进一步冷却收缩时易增加缺陷萌生的概率;而相较于上述因素,相变塑性影响幅度较小。最后,由于马氏体相变体积应变具有闭合缺陷的作用,焊缝中心附近处于受压状态,在力学上其内部组织开裂概率较小,而距离焊缝中心6~8 mm位置,一方面熔合线两侧力学差异较大,另一方面马氏体相变体积分数逐渐减小,缺少一定的抵消作用,因此相比焊缝中心更易开裂,可视为焊缝危险位置。
4 结论
本文建立了1Cr12钢固态相变与焊缝收缩耦合的有限元分析模型,在此基础上,开展了焊接试验件纵向残余应力的验证试验,结果表明纵向焊接残余应力模拟与试验结果吻合。其中,焊缝冷却过程马氏体相变体积膨胀抵消了焊缝收缩作用,使纵向残余拉应力减小;考虑混合相力学性能时,高温奥氏体状态屈服应力小,使受拉塑性过程的峰值拉应力减小,从而使焊缝马氏体相变的拉应力进一步减小,与相变体积膨胀共同促使焊缝进入压缩状态;相反,混合强化作用增大焊缝受拉屈服峰值,但无法抵消相变体积应变和混合相力学性能模型的共同影响;相变塑性在焊缝收缩时产生额外塑性应变,缓和焊缝受力状态,使拉应力减小,但其影响相对较小;综合考虑模型各因素,最终焊缝中心位置附近纵向处于压缩状态。

