用矩阵方法处理物块碰撞次数问题

彭定辉

(江西省南丰县第一中学 江西 抚州 344500)

1 问题

碰撞次数问题是近期网上热议的中学物理问题之一.《碰撞出来的圆周率》一文对此进行了详尽细致的讨论分析，证明了碰撞次数与圆周率的关系[1]；再有《关于物块碰撞次数的探讨》用速度相图方法对该问题进行了研究[2].本文从系统的观点出发，借助矩阵方法，为碰撞次数问题建立一种清晰的物理模型.

为了简化物理情景，故对原题进行部分改动，陈述如下：

图1 变题题图

2 分析

将两物块先相互碰撞，再小物块与墙相碰的过程称为一次冲击，系统运动的整个全过程由多次冲击组成.现就一次冲击中的两次碰撞进行具体分析.

为了凸显运动的对称性，规定小物块m向右为正方向，大物块M向左为正方向.它们之间为弹性碰撞，假定两物块碰前速度分别为v0和u0，碰后速度分别为v和u，故有

-mv+Mu=-mv0+Mu0

求解得

接着小物块m与墙壁发生弹性碰撞，速度反向，故有：v′=-v.可以把v0和u0称为两物块在冲击过程的初速度，v′和u称为对应的末速度.

系统第k+1次冲击时，两物块初速度分别为vk和uk，末速度分别为vk+1和uk+1，故有

(1)

(2)

由于两物块系统能量守恒，即有

(3)

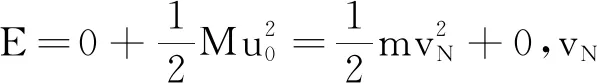
(4)

即能量守恒式(3)简化为

［本刊讯］2012年上海市护理学会团体与个人会费缴纳工作已于本月启动。入会人员需将“会员信息一览表”按样张格式采用Excel电子文档统一录入信息，并在缴纳会费时将电子版与纸质打印版会员信息一并上交备案。集中办理时间:2012年3月27日—28日上午9:00—11:00，下午1:30—3:30，地点:上海市胶州路358弄1号605室。凡交纳2012年个人会费者可享受会员免费讲座2次。逾期未缴纳者，请于2012年4月1日—4月30日内每周二至上海市护理学会(北京西路1623号203室)办理。咨询电话:021－62580348。

V2+U2=1

(5)

(6)

Uk+1=cosθUk-sinθVk

(7)

Vk+1=sinθUk+cosθVk

(8)

此时可以用矩阵来表示此方程组

|k+1〉=P|k〉

(9)

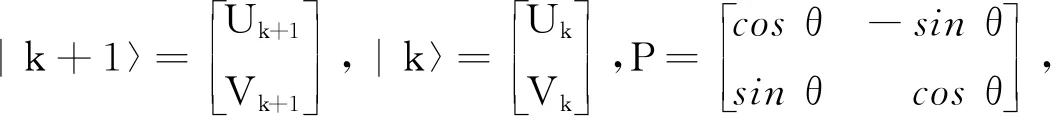
图2 U-V系统状态图

设|k〉状态矢量的相位角为α，即Uk=cosα，Vk=sinα，代入式(7)、(8)，得

Uk+1=cosθcosα-sinθsinα=cos (θ+α)

Vk+1=sinθcosα+cosθsinα=sin (θ+α)

即

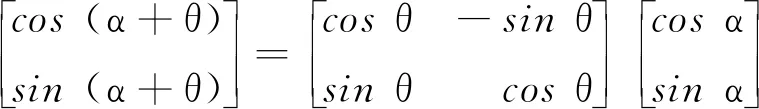
(10)

由上式可知，矩阵P作为作用算符，并不改变状态矢量的大小，仅仅改变状态矢量的相位角，使状态矢量沿逆时针方向旋转θ角.故矩阵算符P也称为旋转矩阵[4].

3 问题解决

其状态矢量的相位角为π.

假设全过程中经过N次冲击，即两物块互碰N次，则有方程

|N〉=PN|0〉

(11)

或

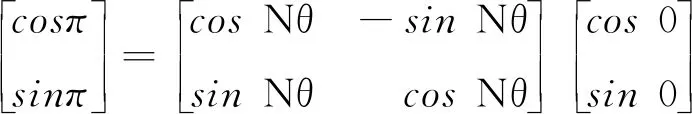
(12)

即PN使状态矢量逆时针旋转Nθ角，刚好使系统的状态矢量的相位角从零增加到π，故有

Nθ=π

(13)

(14)

又由于

且碰撞次数为整数，故两物块相互碰撞的总次数为

(15)

式(15)中“[]”为取整符号.

4 结束语

本文借助量子力学的概念，用状态矢量和矩阵算符描述系统的状态变化，使得物理方程形式简洁，意义明确；状态转换式

|k+1〉=P|k〉

从某种角度来说具有物理通用性，对于同类问题有一定的参考价值.