特快速暂态过电压信号下的屏蔽线端口串扰电压分析

刘寒春,周建明,刘守城,赵 阳

(1.江苏省医疗器械检验所,江苏 南京 210019) (2.南京师范大学南瑞电气与自动化学院,江苏 南京 210023) (3.南京师范大学江苏省电气装备与电磁兼容工程实验室,江苏 南京 210023)

随着电网运行电压等级的提高,GIS中的隔离开关运动速度较慢,其绝缘气体易被击穿,形成一系列的电磁暂态现象,尤以VFTO现象最为频繁. 目前,关于VFTO的相关研究已趋于成熟,大致可分为以下 4个方面:信号的产生方式[1]、信号的实地测量方法[2]、信号的波形特征[3]和信号的抑制方法[4]. 现有的研究大都趋向与研究VFTO源这一方面,对于其传输特性的研究则较少. 该信号由于其幅值大、组成频率复杂,在通过电力线缆传输至二次侧后极易对敏感设备造成电磁干扰. 因此,对于VFTO信号的传输特性研究具有重要意义.

屏蔽线缆有良好的屏蔽性能和传输性能,被广泛地应用于包括电力工业的多个领域. 但金属编织屏蔽层存在诸多网孔,高频电磁能量依旧可以耦合发散影响外围设备. 关于屏蔽线的串扰问题于1981年由Paul[5]提出,利用频域链参数的方法计算了3种不同线型情况下的串扰响应. 之后有诸多学者研究屏蔽线之间的串扰,当前主流的方法为将整个模型拆分为内、外传输线系统并分别求解[6-9]. 两个系统由屏蔽层的转移阻抗和转移导纳联系起来,关于转移阻抗的计算方法目前也有多种方法:Vance模型[10],Tyni模型[11],Demoulin模型[12]等. 最后,利用时域有限差分法对于内、外传输线系统的电报方程进行求解即可得到线缆端口处的串扰响应.

1 VFTO信号分析

由于GIS隔离开关在分合闸操作时,动触头运动速度较慢导致开关断口间的气体间隙发生多次预击穿现象. 每一次击穿均会产生一次陡变的电压行波,多次行波发生折射、反射和叠加,产生了VFTO,类似于雷电现象. 这种信号在GIS内部易通过输电线缆传输至二次侧,对其余线缆、设备等产生严重影响.

VFTO信号并不具备标准波形,其随着变电站的内部结构、电压等级等发生变化,且通过实验获取其数据成本过高. 因此本文借用ATP-EMTP软件,通过仿真获得VFTO的波形数据,进行下一步分析. 我们在软件中搭建了文献[13]中的短母线开路的ATP-EMTP仿真模型,并在负载侧获得其时域波形如图1所示. 源端幅值为100 kV,时间步长为1 ns,总时长为1 μs. 从时域图中我们可以看出,在发生击穿现象后,负载侧会传输超过标幺值的电压,且由多种波形叠加而成. 为了便于下一步的分析,我们还需要了解构成这一波形的各频率分量,目前常见的方法为快速傅里叶变换.

经过在高频段(1 MHz～1 GHz)快速傅里叶变换之后,发现VFTO信号除工频分量外,还存在着几类高频分量. 由图2可见,除了8 MHz主导频率外,VFTO波形中还含有40 MHz、56 MHz、88 MHz等频率分量,其分别对应8 MHz的5次、7次和11次谐波频率分量. VFTO频率分量的得出对于之后屏蔽层转移阻抗的计算是不可或缺的.

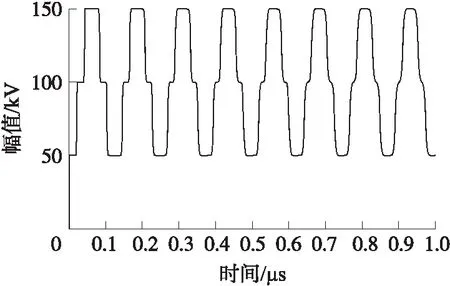
图1 VFTO时域波形Fig.1 VFTO time domain waveform

图2 VFTO频率分量Fig.2 VFTO frequency component

图3 RG58屏蔽线转移阻抗计算值Fig.3 Calculated value of transfer impedance of RG58 shielded cable

2 屏蔽线与单芯线的内外回路建模

目前对于单线和屏蔽线的串扰问题大都将其分为内、外两个传输线系统,其中外传输线系统由单线、屏蔽层和参考地组成,内传输线系统由屏蔽层和屏蔽线的内芯线组成. 两个传输线系统通过屏蔽层的转移阻抗和转移导纳联系,由于转移导纳与转移阻抗的影响非常小,故在多数研究中均将其忽略不计.

转移阻抗定义为单位长度线缆上单位电流流过屏蔽层时,在屏蔽层与内芯线之间所形成的开路电压:

(1)

式中,I0为屏蔽层中流过的电流,∂V/∂Z为内芯线与屏蔽层之间的单位电压. 在本文中我们参考了Kley[14]转移阻抗计算模型:

Zt=Zd+jωLt+(1+j)ωLs.

(2)

式中,Zd为编织网孔线缆转移阻抗的散射部分,Lt为透射电感,Ls为编织网孔处的滋生涡旋电感. 在屏蔽线参数确定的情况下,转移阻抗只与频率相关. 本文中所选用屏蔽线型号为RG58,其屏蔽层各项参数固定,我们可由公式(2)得到其转移阻抗与频率的关系图(如图3所示).

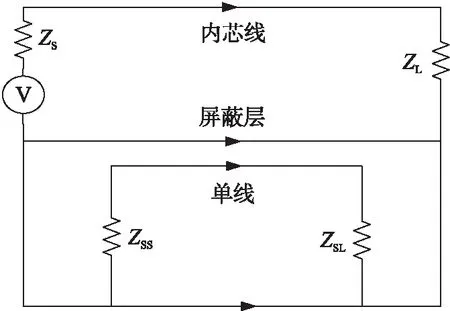
图4 屏蔽线与单芯线等效电路模型Fig.4 Shielded cable and single core cable equivalent circuit model

2.1 内传输线回路

上文中提及由单芯线和屏蔽线组成的模型形成了两组传输线回路,其中屏蔽线内芯线施加信号,并在屏蔽层上产生感应电流,进而影响单芯线,并在其端口处产生感应电压. 其等效电路模型如图4所示,图中电阻ZS,ZL,ZSS,ZSL均为50 Ω,屏蔽层两端直接接地.

依据传输线理论,内芯线上的电流分布为:

(3)

式中,I01和Z01表示内芯线激励电流和内阻抗,ZC1和γ1表示内传输线回路特征阻抗和传播常数. 由于屏蔽层不含激励源,则内芯线上的电流在屏蔽层任意位置z处产生的分布电压源为:

du=I1(z)Ztdz.

(4)

2.2 外传输线回路

对于由屏蔽层、单芯线和参考地组成的外传输线回路,其电报方程见式(5)、式(6):

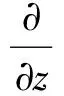
(5)

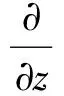
(6)

式中,R、L、C、G分别为传输线的单位长度电阻、电感、电容、电导参数矩阵,在ANSYS软件中建立截面模型,利用2D Extractor Design模块提取参数矩阵,V、I为电压、电流矩阵. 本文采用无条件稳定的implicit-wendroff差分格式的时域有限差分法对该方程组进行求解[15]. 此时,回路中无集总电源激励,激励为屏蔽层上的分布电压源.

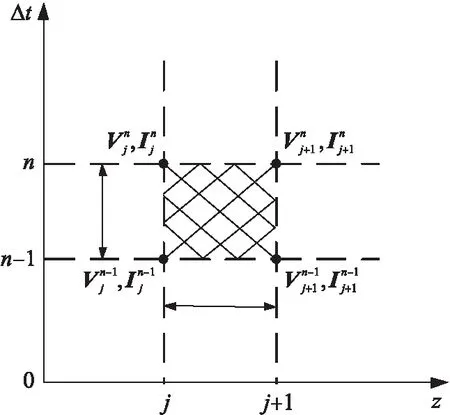
图5 Implicit wendroff差分格式节点分布Fig.5 Implicit wendroff difference format node distribution

使用implicit-wendroff FDTD方法对式(5)、式(6)进行差分计算. 该差分格式不存在传统的FDTD方法在划分空间和时间时上的稳定性问题,其计算效率高.

传输线一共被分为NDZ段,每一空间步长为Δz;总求解时间一共被分为NDT段,每一时间步长为Δt.如图5所示,通过利用差分代替微分的思想,对一特定位置z,时间t,U(z,t)可被表示为:

(7)

(8)

(9)

然后,式(5)、式(6)可离散化为:

(10)

(11)

进一步简化为:

(12a)

(12b)

式中,

AVj=-(Rj/2+Lj/Δt)Δz,

(13)

BVj=-(Rj/2-Lj/Δt)Δz,

(14)

AIj=-(Gj/2+Cj/Δt)Δz,

(15)

BVj=-(Gj/2-Cj/Δt)Δz,

(16)

(17)

对上式进行空间和时间上的离散,该差分格式下空间和时间的划分段数无需满足魔幻步长条件,计算速度有较大提升. 外加两端边界负载条件,将上式进行化解,可分别得到电压和电流的迭代公式,最终得到单芯线两端的电压暂态响应波形.

3 数值仿真验证

对具体模型中的串扰进行理论计算与仿真验证,其中屏蔽线型号为RG58,单芯线型号为AWG23,其径向和截面示意图如图6所示. 模型的具体参数如表1所示.

图6 串扰模型示意图Fig.6 Schematic diagram of crosstalk model

表1 RG58和AWG23线缆参数Table 1 RG58 and AWG23 cable parameters

图7 单芯线两端口响应电压波形Fig.7 Single core cable two-port response voltage waveform

我们在CST CABLE STUDIO软件中建立了该模型,并将VFTO信号作为激励源,得到了内芯线上的信号对于单芯线的串扰影响. 用MATLAB软件计算得到理论值,对比如图7所示. 对于近端电压而言,在正半周期内,计算值会稍小于仿真值,而在负半周期内,计算值会稍大于仿真值,计算值曲线整体呈现下移,远端电压则相反,计算值曲线整体呈现上移. 且由于采样点密度的关系,计算曲线无法达到仿真曲线类似的密集波动,但是能够在整体趋势上达到高度吻合,验证了方法的有效性. 在峰值处存在着一些误差,大致来源于以下3个方面:(1)传输阻抗的理论计算值与实际值不会达到完全吻合. (2)ANSYS软件提取R、L、C、G参数矩阵时运用的有限元算法与CST软件的有限积分算法存在误差. (3)时域有限差分法本身受其分段精度的影响存在误差.

在之后的工作中,可以通过变电站的实测输入信号数据、线缆型号、接地方式等相应调整文中模型. 进一步研究各参数对于串扰、衰减等的影响,通过计算机仿真辅以实地验证的方法确定如何布置使得信号经线缆传输后对于周围设备影响最小.

4 结论

本文建立了以屏蔽线和单芯线为主体的线缆串扰模型,其中屏蔽线的内芯线接有VFTO信号. 经过快速傅里叶变换之后发现,VFTO信号中存在高频分量,易由屏蔽层中网孔泄露出去造成串扰. 通过将该模型拆分为内、外传输线回路,并利用传输阻抗这一概念将其联系起来,得到了3个导体电压、电流之间的函数关系. 最后利用implicit-wendroff差分格式下的FDTD对其进行求解. 结果表明,该方法与仿真值基本吻合.