水位骤降条件下强透水基础岸墙填土渗流分析
吴 博,赵坤朋,黄岳文,刘华北
(1.华中科技大学土木工程与力学学院,湖北 武汉 430074;2.广州市水务工程建设管理中心,广东 广州 510640)
水利工程中的一些挡土墙在建造和使用期间常常会发生墙前水位骤降现象,这对挡土墙的稳定是不利的,但目前对于水位下降时挡土墙稳定性的研究还比较缺乏。挡土墙的稳定性主要与作用在挡土墙上的侧压力即土压力与水压力有关,目前水压力往往直接按静水压力处理,而土压力的研究也多基于饱和土和稳定渗流状况,对于非饱和土瞬态渗流的研究甚少[1]。实际上墙前水位下降过程中墙前后水位降幅是不同的,此时作用在墙上的水压力计算应考虑到墙前、墙后水位差变化问题。
由于当前工程界缺乏简单合理的渗流分析工具,目前挡墙的稳定分析中,墙前水位骤降的条件下,往往对墙后填土的水位采取简化假定来进行稳定性校核,未合理考虑地基的透水性以及填土的渗流。如墙前水位采用设计(校核)洪水位、墙后水位采用平墙顶(或地下最高水位),或取墙前洪水位高度骤降到常水位、墙后水位高度取墙前洪水位下降高度的60%[2]。GB 50707—2011《河道整治设计规范》[3]附录B建议挡墙稳定性计算时取水位骤降1m、设计枯水位以及不利于中水位3种情况。SL 379—2007《水工挡土墙设计规范》[4]5.2.5条指出,当挡土墙修建于潮汐河道上时,最不利条件的墙前、墙后水位差取相应最大潮差值的1/3~1/2 较为合适;对于在水库或者退水较快的行洪道上的挡土墙,在考虑墙前水位骤降的情况下,挡土墙稳定性的最不利水深取墙前、墙后最大水位差的0.5 倍;当挡土墙修建于无潮汐影响河道上时,挡土墙在正常运营期间受降雨以及渗流滞后的影响,其墙前、墙后水位差的取值为0.5~1 m。欧美相关规范[5-6]同样对墙后设计水头的规定比较模糊,只是建议根据排水和墙后填土的情况具体问题具体分析。例如,美国桥梁设计规范[7]中没有明确规定挡土墙后的设计水位,仅提出必须予以考虑。
有限差分法是计算机数值模拟最早采用的方法,至今仍被广泛运用。夏元友等[8]用有限差分法软件建立了二维边坡非饱和渗流稳定性分析模型,并将该模型用于考虑降雨入渗影响的边坡稳定性计算。蒋中明等[9]编写了降雨入渗及停雨出渗时的三维边坡边界函数,对基于有限差分法的软件进行了非饱和渗流分析的功能完善,实现了降雨条件下三维边坡非饱和渗流模型的模拟。An等[10]利用坐标变换方法建立了一个多维的有限差分模型来模拟饱和-非饱和渗流,该模型可以处理非正交网格,可用于分析几何形状复杂及各向异性的渗流模型。
对于水利工程常用的岸墙结构,为了保持在水位骤降条件下良好的透水性,往往在岸墙基础设置一定厚度的强透水层。墙前水位骤降时,由于强透水基础的作用,岸墙墙后填土底部的水头与墙前水头差别很小。本研究根据强透水基础岸墙的这一特点,利用一维的渗流微分控制方程建立非饱和土渗流的数学模型,通过有限差分法编写MATLAB程序对水位骤降条件下非饱和土的渗流进行研究,并与模型试验和数值模拟的方法所得结果进行对比,验证程序计算结果的可靠性。同时利用所编写的MATLAB程序分析模型参数对非饱和土渗流的影响程度,以便更好地分析非饱和土水位骤降过程中孔隙水压力分布的规律。
为了减小墙前后的水位差,通常还在挡土墙上布设排水孔来增加抗渗稳定性和降低墙后水位,进而起到减少静水压力的作用,保障挡土墙抗滑稳定[11]。由于本文研究中采用的强透水基础已经有较好的排水效果,故不再考虑排水孔的布设。
1 一维瞬态渗流方程差分形式
取单元土体,对于一维渗流情况考虑单位时间内流入和流出微元体的水量差应满足水流连续方程,即
(1)
式中:vy——y方向的渗流速度;θ——单位体积含水量;t——时间。

(2)
式中:ky——y方向的渗透系数;H——总水头。
单位体积含水量随时间变化可用下式表示:
(3)
式中:uw——水压力;ρw——水的密度;g——重力加速度。
达西定律最初是由饱和土得来,但之后的研究证明其也能应用于非饱和土渗流[12-13]。唯一的区别在于非饱和土的渗透系数不再是常数,而是随含水量的变化而变化。储水曲线斜率mw的值同样是随含水量的变化而变化。下文中差分程序计算所用到的渗透系数ky以及储水曲线斜率mw随含水量变化的关系式均由SEEP/W软件[14]中的样本函数获得。
将式(2)(3)代入式(1),由于高程y对时间导数为0,可得一维瞬态渗流控制方程:
(4)
对于水位骤降下的一维渗流,边界条件如下:
H(y,0)=H0
(5)
H(0,t)=H0-vt
(6)
式中:H0——墙前初始水位;v——水位下降速度。
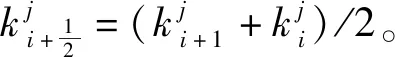
(7)
边界条件可写为
(8)
(9)
令a=Δt/(ρwgΔy2),式(5)可写为

(10)
2 差分程序验证
根据以上方程编写MATLAB差分程序,程序流程如图1所示。为确保所编写的MATLAB差分程序计算结果的可靠性,利用SEEP/W数值模拟软件以及模型试验对程序计算结果进行标定,为后文研究提供分析依据。
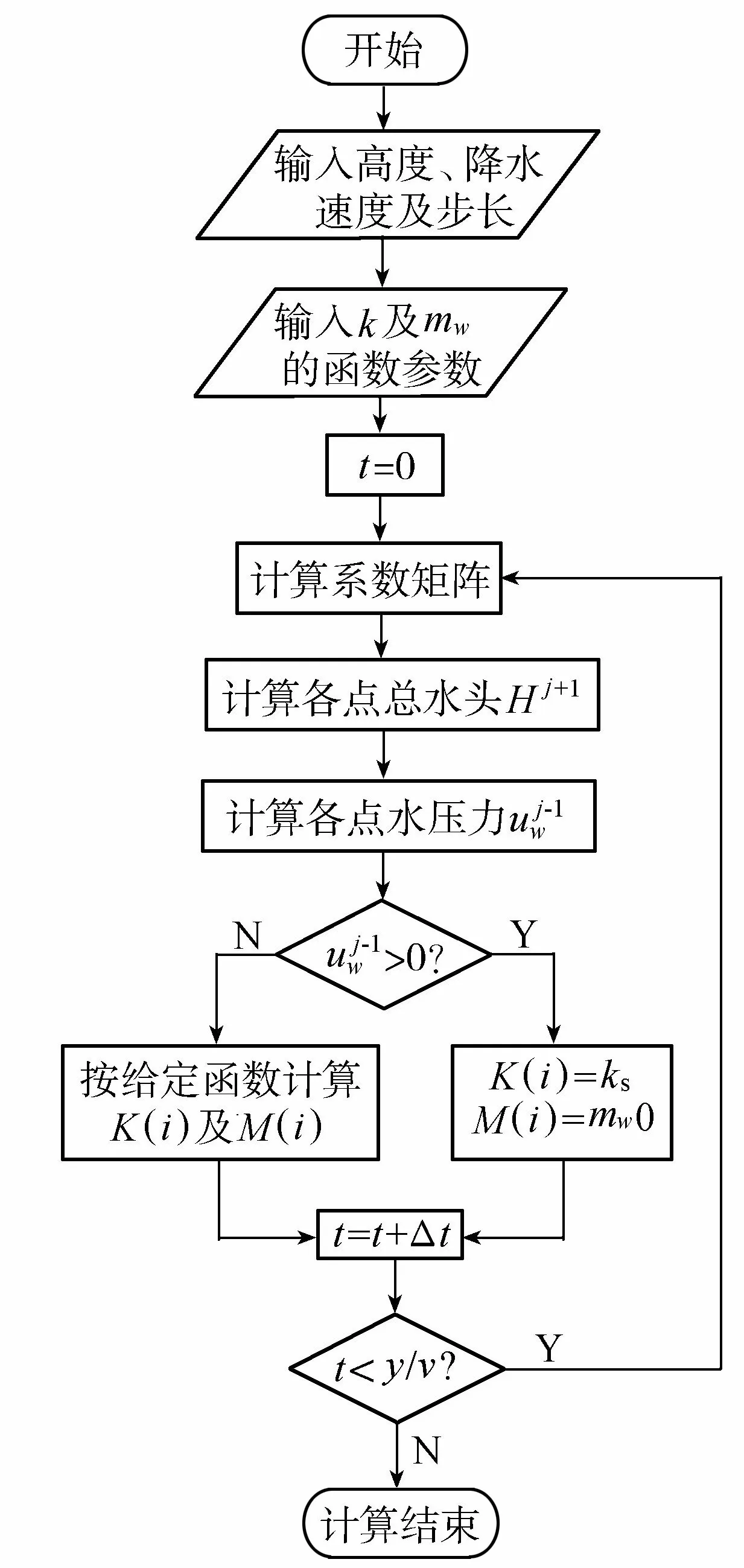
图1 程序流程Fig.1 Flow chart of program
2.1 数值模拟简介
本研究中数值模拟用GeoStudio系列软件中的SEEP/W软件完成。SEEP/W软件是一款能够全面处理非饱和土体渗流问题的有限元分析软件,具有强大的渗流分析功能,被广泛用于岩土工程相关的渗流问题分析[14-15]。
2.2 模型试验简介[16]
模型试验在自制的大型模型箱内进行,模型箱宽1 m,高2.1 m,墙前蓄水空间长0.9 m,墙后填土空间长2.1 m。试验填土高度为2 m,并在挡墙前后铺有20 cm厚碎石,剖面图如图2所示。试验用土采用分层填充、分层击实的方法填入,并每隔0.2 m采用环刀法进行密实度检测,保证填入土体的均匀性。

图2 试验模型剖面图(单位:mm)Fig.2 Cross illustration of model tests (units:mm)
试验用土为中砂,其物理参数依据GB/T 50123—1999《土工试验方法标准》[17]室内试验测得,其湿密度为1.72 g/cm3,平均含水率为2.79%,最大、最小干密度分别为1.89 g/cm3、1.45 g/cm3,中砂及铺设的碎石饱和渗透系数分别为3.8×10-5m/s、0.005 m/s。
填土过程中在填土纵轴面处预埋振弦式通气型渗压计,用于测量墙前水位骤降过程中墙后填土的水压力变化,渗压计分3层埋设。
2.3 一维渗流模型验证
利用SEEP/W软件建立一维渗流模型,模型为高2 m砂层,砂土各参数取值同上,各点初始总水头均为2 m,底部边界总水头以1 m/h的速度降低。用上述MATLAB差分程序计算该模型,得到不同水位时压力水头与高程的关系,并将结果与SEEP/W计算结果进行对比,如图3所示。
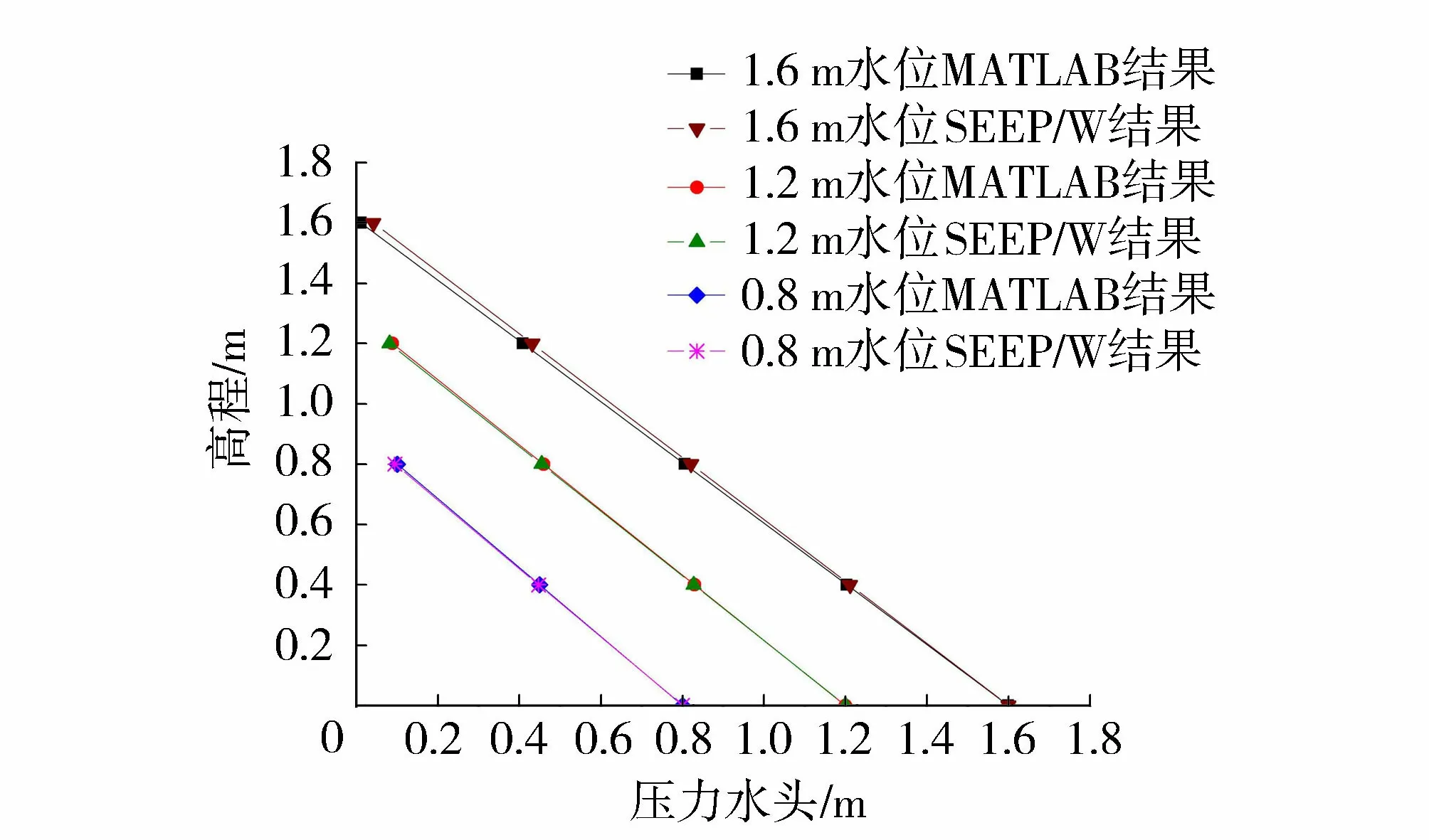
图3 一维模型压力水头与高程的关系Fig.3 Relationship between pressure head and elevation of one-dimensional model
2.4 强透水基础二维渗流模型验证
以0.5 m/h降水速度进行模型试验,用渗压计测得降水过程中各测点的水压变化。同时利用SEEP/W软件模拟试验模型如图4所示,模型尺寸、各材料参数和边界条件与模型试验一致,网格尺寸为0.05 m。图中A1~A3、B1~B4、C1~C4表示试验模型中3层渗压计埋设的位置。DE、EF代表模型不透水边界条件,DG代表模型初始水头边界,GH代表墙前水位下降初始高度。将模型试验、数值模拟以及MATLAB程序求解得到的结果进行分析比较,如图5所示。

图4 数值模型Fig.4 Numerical model
从图5可以得出:MATLAB计算的压力水头与数值模拟和模型试验得到的压力水头基本吻合,因此对于强透水基础的二维渗流模型,可将其简化成一维模型计算,用本研究所编写的程序能对其进行分析。

图5 二维模型压力水头与高程的关系Fig.5 Relationship between pressure head and elevation of two-dimensional model
3 不同参数对渗流的影响
基于以上研究,利用MATLAB程序研究降水速度、渗透系数以及土的饱和含水量对水位骤降条件下渗流的影响。本节建立的MATLAB计算基本模型为高6 m粉土,渗透系数为10-7m/s,土的饱和含水量为0.3 m3/m3,各点初始水头均为6 m,底边总水头以1 m/h速度减小。
3.1 降水速度对渗流的影响
在基本模型的基础上,分别取降水速度为0.5 m/h、1 m/h、1.5 m/h、2 m/h进行计算,将不同降水速度结果进行对比,如图6所示。

图6 不同降水速度下压力水头与高程的关系Fig.6 Relationship between pressure head and elevation with different drawdown speeds
3.2 渗透系数对渗流的影响
在基本模型的基础上,改变土的渗透系数进行计算,共取了6种不同渗透系数k,将各组结果进行对比,如图7所示。
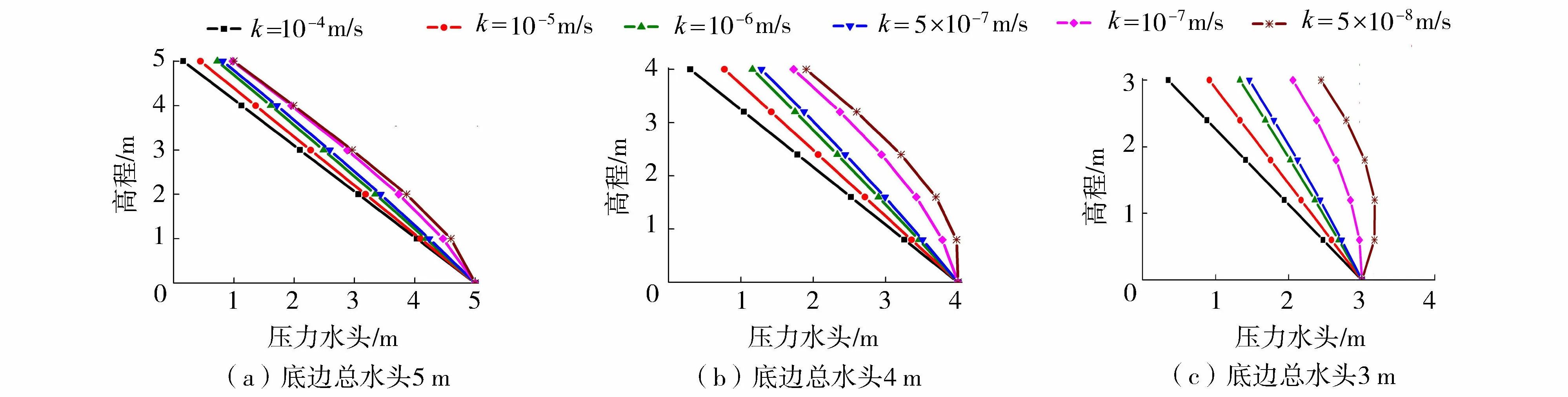
图7 不同渗透系数下压力水头与高程的关系Fig.7 Relationship between pressure head and elevation with different permeability coefficients
各类土体渗透系数k的量级如下:砾石、粗砂为10-4~10-3m/s,中砂为10-5~10-4m/s,细砂、粉砂为10-6~10-5m/s,粉土为10-8~10-6m/s,粉质黏土为10-9~10-8m/s,黏土为10-12~10-9m/s[18]。可以看到本研究中讨论的渗透系数范围包含了除渗透性较低的黏土外的各类土体,根据图7可以判断各类土体在水位骤降过程中压力水头的变化规律。
3.3 饱和含水量对渗流影响分析
在基本模型的基础上,计算中分别取土的饱和含水量为0.3 m3/m3、0.4 m3/m3、0.5 m3/m3、0.6 m3/m3,对比不同饱和含水量的计算结果,如图8所示。
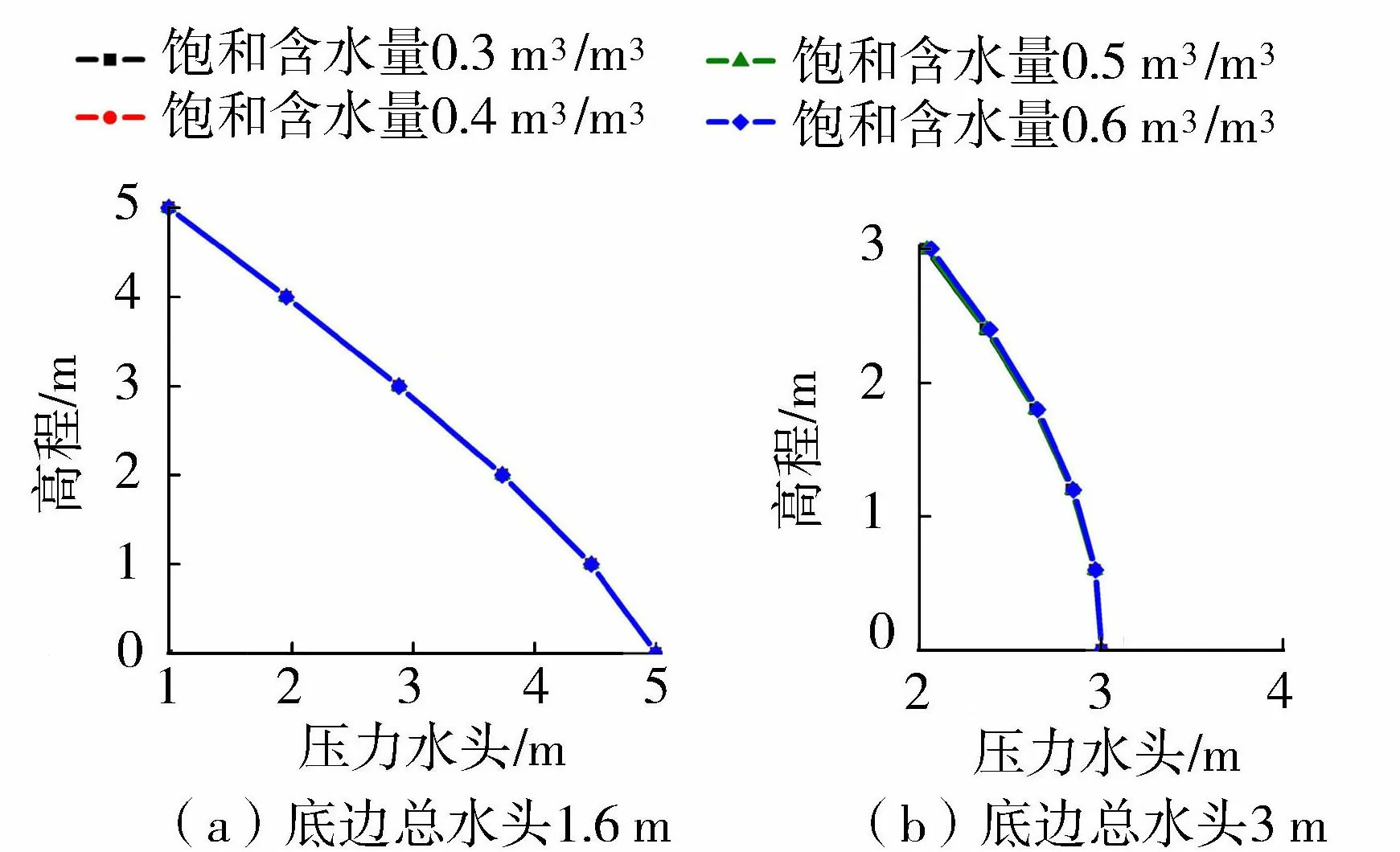
图8 不同饱和含水量下压力水头与高程的关系Fig.8 Relationship between pressure head and elevation with different water content of saturated soil
从以上结果可以看出,降水速度和渗透系数均对降水过程中水压变化有较大影响,不同降水速度和渗透系数得到的压力水头曲线有明显差异,而不同土的饱和含水量得到的压力水头曲线几乎重合,说明其对水位骤降条件下的渗流过程影响不大。
4 结 论
a.MATLAB计算结果与一维渗流数值模拟结果对比得出,MATLAB程序可以准确地计算一维渗流模型水位骤降过程中的水压力变化,为水位骤降条件下强透水基础岸墙填土渗流分析提供了分析方法。
b.MATLAB计算结果与模型试验和二维渗流数值模拟结果对比得出,对于强透水基础的挡土墙水位骤降情况,可将二维渗流模型近似看作一维渗流模型计算,用本文编写的程序仍能计算得到较精确的结果。
c.在文中研究范围内,土的渗透性对水压力变化的影响较降水速度大,而土的饱和含水量对水压变化几乎无影响。

