基于TMD控制的浮式风力机稳定性研究
蔡 新,张洪建
(1.河海大学力学与材料学院,江苏 南京 211100;2.沿海开发与保护协同创新中心,江苏 南京 210098;3.江苏省风电机组结构工程研究中心,江苏 南京 210098)
浮式风力机处于复杂的海洋环境中,会受到包括风、浪、流、冰等各种外部载荷的作用。这些外部载荷影响浮式风力机的稳定性,并可能导致其部件故障甚至破坏。为了降低海上风力机组的载荷并提高浮式风力机的稳定性,许多学者对此进行了研究,主要分为三方面:(a)利用控制桨距的方法减小气动载荷从而提高浮式风力机的稳定性,包括独立变桨控制[1]、发电机转矩控制[2]以及气动转子控制[3]。这种方法对浮式风力机可以产生一定的控制效果,但是复杂的桨距控制策略会增加叶根的疲劳载荷。(b)通过对支撑结构的设计提高浮式风力机的稳定性。Kim等[4]研究了系泊系统对Spar浮式风力机的影响;丁勤卫等[5]研究了垂荡板布置形式与数量对Spar浮式风力机的影响;黄致谦等[6]设计了一种新型半潜式平台并与已有的平台进行了对比。然而这些研究通常把研究重点放在浮式平台的设计上,而将风力机上部简化为一个集中质量,无法研究浮式风力机上部的非线性动力学特性。(c)结构控制。结构控制一般用于高层建筑物减振的研究中,海上浮式风力机高度基本在100 m以上,因此可以借鉴结构控制的方法来提高浮式风力机的稳定性。结构控制分为被动控制与主动控制,主动控制可以降低浮式风力机的疲劳载荷,但也会降低其功率[7]。被动控制成本较低,不会影响发电效率,由于减振作用明显,故主体结构可以减小构件截面尺寸,降低成本。诸多学者研究了不同形式的被动结构控制方法,如调谐液体阻尼器[8]、调谐液体柱阻尼器[9]、摩擦阻尼器[10]以及调谐阻尼质量器(tuned mass dampers,TMD)[11]等。浮式风力机机舱内空间狭小,同等质量混凝土的体积仅为水的1/3,因此TMD更适合浮式风力机。但是TMD往往不能宽频吸振,一旦结构振动频率与自振频率相差过大,控制效果会大幅下降,甚至加剧振动。
通过以上研究可知,对提高浮式风力机稳定性的研究取得了很多成果,但仍有不足之处:变桨控制系统可以降低气动载荷,但会增加叶根疲劳载荷;设计支撑结构时会对浮式风力机上部进行简化,不能真实反映浮式风力机运动状况;而结构控制与质量、弹簧和阻尼的参数组合密切相关。目前关于TMD参数优化的文献大部分基于批量计算,从大量输出结果中选取较优的结果,以达到参数优化的效果。一旦浮式风力机参数发生变化,又要重新计算,时间成本大大增加。本文利用FAST模拟结构的动力特性研究TMD对浮式风力机稳定性的影响,考虑了风浪耦合作用,模拟浮式风力机的运动响应。基于遗传算法对TMD结构参数进行优化,通过研究TMD各个参数对浮式风力机整体运动方式的影响来设置目标函数,不同的浮式风力机只需要修改目标函数中对应的参数,改变算法中迭代次数等参数。结果表明,该方法可以明显提高计算精度,减少计算时间。
1 浮式风力机模型
利用NREL开发的FAST作为模拟海上风力机性能的主要工具。研究对象为NREL 5MW Barge风力机组,为水平轴三叶片风力机,控制方式为独立变桨控制,轮毂高度为90 m,叶轮直径为126 m,风力机总质量为697 t[12]。
Barge浮式平台结构形式如图1所示。其优点是节省成本,便于现场安装。但是由于其大部分结构在水面之上,所以其对波浪载荷非常敏感。Barge浮式平台为一个40 m×40 m×10 m的长方体,吃水深度为4 m,平台质量为5 450 t。系泊系统由8根系泊缆组成,长度为473.3 m,单位长度质量为130.4 kg/m[13]。

图1 Barge浮式平台示意图Fig.1 Diagram of Barge platform
2 模 型 建 立
2.1 风场模型建立
为模拟湍流风,设定风场面积为150 m×150 m。考虑空间相干性,利用风模拟软件Turbsim生成以Kaimal风谱模型为基础的风速分布模型[14],其风谱模型为
(1)
式中:f——频率;S(f)——功率密度;σ——速度标准差;L——湍流尺度参数;V——轮毂处风速。
以风力机叶轮中心为参考风速点,设定风力机的额定风速11.4 m/s为参考点风速,仿真时间为10 min,得到符合实际情况的湍流风场。风场计算区域及网格划分如图2所示,叶轮中心处风速分布如图3所示,图3中x轴正向为0°湍流风传播方向;y轴由右手定则确定;z轴竖向朝上。
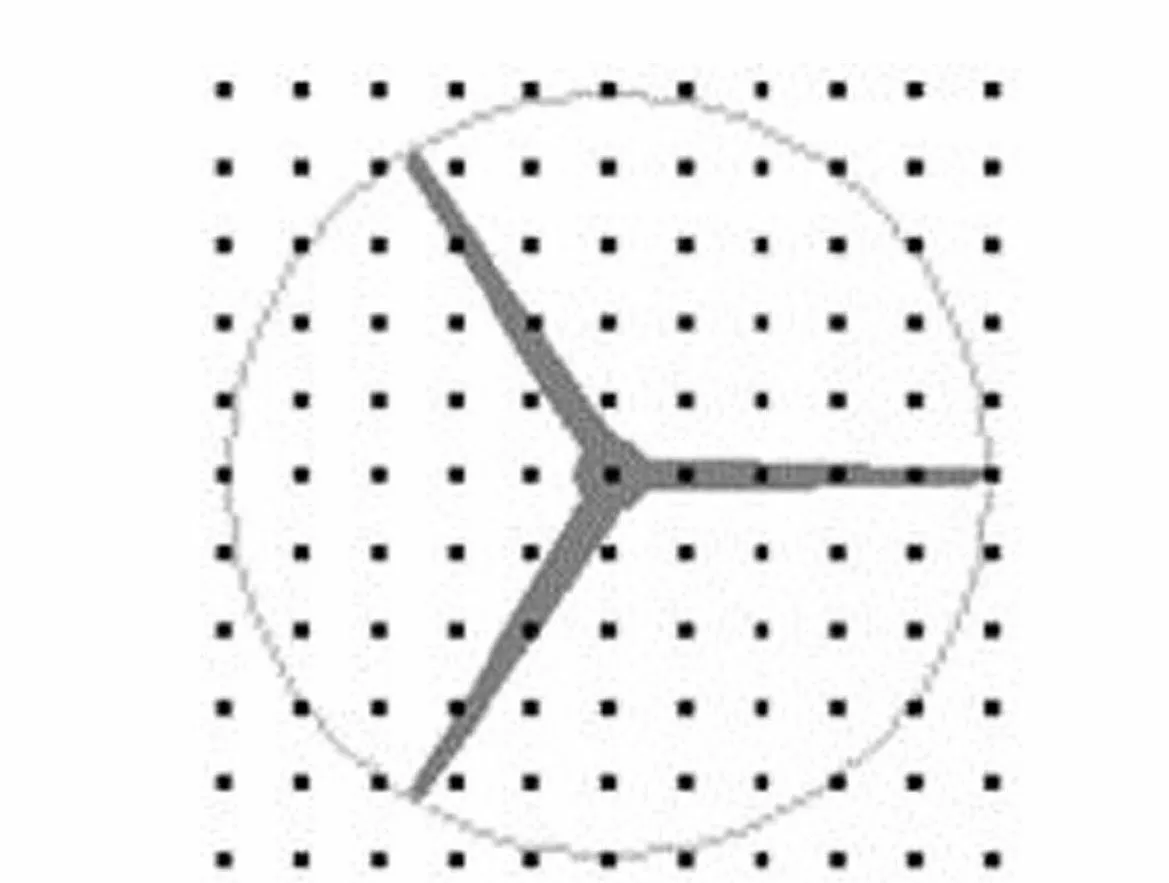
图2 风场计算区域及网格 Fig.2 Calculation region and grid of wind field
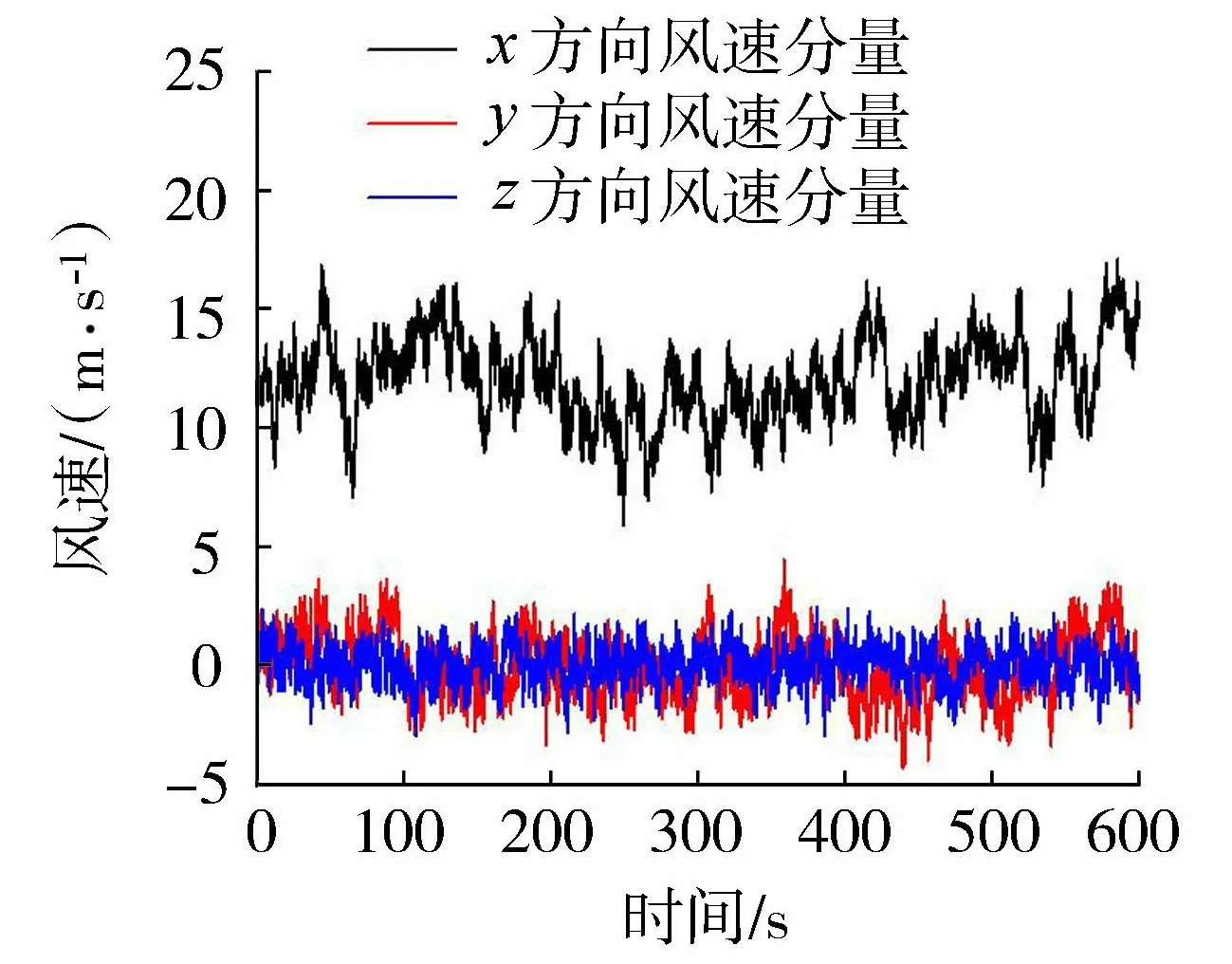
图3 时域风速Fig.3 Wind velocity in time domain
2.2 波浪载荷模型建立
常见的波浪谱有PM谱、Jonswap谱、BM谱以及文圣常谱等[15]。选择实际工程中较为常用的PM波浪谱[16],可表示为
(2)
式中:Sζ(ω)——波浪功率谱;U——波浪传播速度;ω——波浪圆频率;g——重力加速度。
设定波浪谱波高为5 m,波浪周期为12.4 s。得到充分发展的波浪如图4所示。

图4 波浪时程Fig.4 Wave in time domain
2.3 TMD模型建立
建立TMD模型的关键在于将TMD系统运动方程与风力机原始运动方程进行耦合。机舱中TMD原理如图5所示。风力机动力学模型可用Kane方程表示:
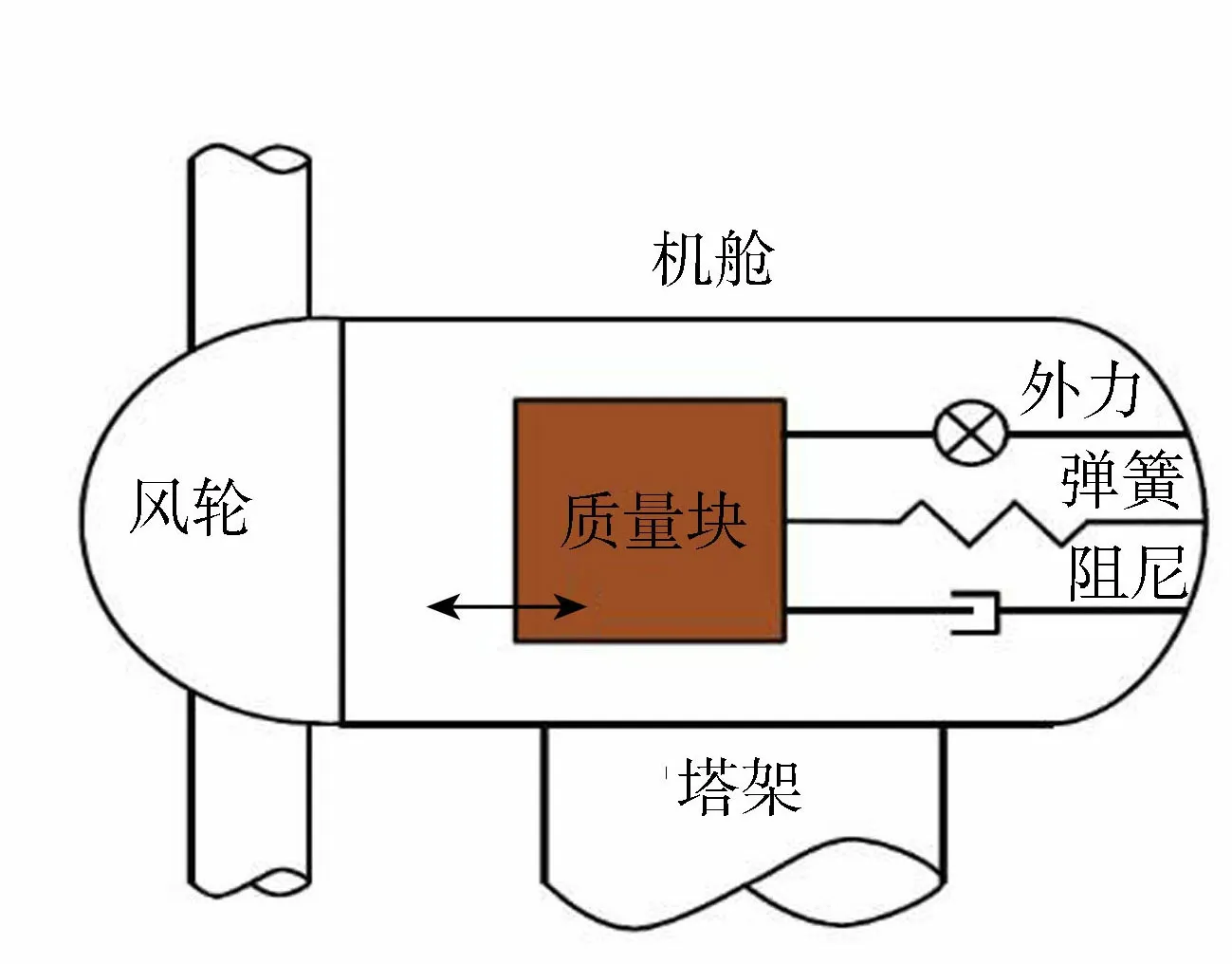
图5 机舱中TMD原理Fig.5 Principal diagram of TMD in nacelle
(3)
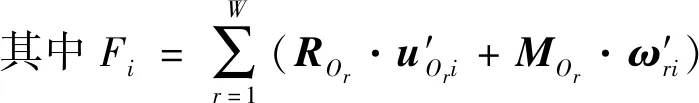

风力机在配置TMD系统后,仅在原有风力机模型上耦合了新的自由度,新的动力学方程中多了与TMD自由度相关的主动力和惯性力项。推导过程给出如下假设:TMD系统位于机舱内,并在机舱坐标系中进行移动;TMD位置是相对于塔顶中心确定的;忽略TMD系统的转动效应。TMD系统位于机舱底部,由质量系统、弹簧系统和阻尼系统组成。TMD通过预先人为设置质量、刚度与阻尼,使自振频率接近于风力机自振频率。当TMD在外力作用下产生振动时,TMD会产生与主体结构振动方向相反的惯性力,能量通过阻尼耗散,达到结构稳定控制的目标。TMD系统运动方程为

(4)

(5)
式中:X——支撑系统位移;x——TMD位移;d——TMD阻尼;k——TMD刚度;K——支撑系统刚度;M——支撑系统质量;m——TMD质量;F(t)——外部负载。
由振动力学原理可以得到主系统振动响应A为
(6)


3 TMD系统参数优化
遗传算法的原理是通过模拟物种进化从而得到最优解。遗传算法相较于其他优化算法速度更快、更准确,并且能够自动调整搜索方向,其主要过程为首先随机产生一个初始种群,之后按照优胜劣汰的原则,进化出更加符合要求的结果,根据目标函数与约束条件来选择个体,并进行交叉与变异生成新的种群,最后得到满足要求的最优结果[17]。遗传算法流程如图6所示。
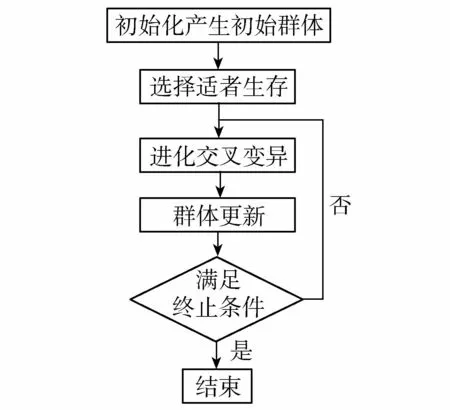
图6 遗传算法优化流程Fig.6 Optimization flow chart of Genetic Algorithm
TMD系统主要包括质量系统、刚度系统和阻尼系统,说明结构参数主要表现为质量、刚度和阻尼的变化影响浮式风力机动力响应,通过调整各项参数使TMD吸收更多结构振动产生的能量,从而减小结构振动响应。采用遗传算法作为优化方法对质量、刚度和阻尼数值进行优化,目标函数为使TMD系统自振频率接近浮式风力机自振频率。根据TMD设计的相关规范[18],确定各参数计算取值范围:10 t≤m≤40 t,5 kN/m≤k≤25 kN/m,6 kN·s/m≤d≤25 kN·s/m。
利用Matlab编写优化算法程序,其中算法控制进化的参数中交叉概率、变异概率及进化代数分别为0.65、0.08与2 000。得到优化后的TMD质量为20 902 kg,刚度为8 374 N/m,阻尼为22 830 N·s/m。高耸建筑结构中,TMD质量一般占结构整体质量的0.25%~2.00%。本文TMD质量占结构总质量的0.34%,符合质量比要求。
4 结果与分析
海上浮式风力机组稳定性主要表现为平台运动响应与塔顶位移,而塔架载荷大小决定了风力机组的可靠性与安全寿命,故以平台运动、塔顶位移与塔架根部载荷为研究重点。初始TMD为根据Den Hartog原则[19]确定的参数,质量20 t,弹簧刚度10 kN/m,阻尼50 kN·s /m。风浪均垂直于叶轮。
4.1 TMD对平台稳定性的影响
由图7可知:TMD对平台纵荡、横荡和垂荡影响较小,对横摇、纵摇和首摇影响较为明显,优化TMD相较于无TMD控制效果更好;优化TMD使横摇范围从1.51°~-1.32°降低为0.98°~-0.82°,降幅达35%;纵摇范围从12.05°~-10.77°降为10.87°~-9.18°,降幅达9.8%;首摇范围从11.12°~-8.72°降至9.18°~-8.83°,降幅达17.4%。由此可见,TMD对平台影响主要体现在抑制平台转动。究其原因,浮式风力机平动周期相较于转动周期更大,TMD自振频率更接近浮式风力机转动频率。而TMD仅在水平方向运动,故对垂荡影响很小。

图7 平台运动6自由度时历运动曲线Fig.7 Motion curve of platform motion with 6 DOFs
4.2 TMD对塔顶位移的影响
由图8可知:TMD使塔顶各向位移均有减小,优化TMD的控制效果则更加明显;塔顶前后位移从2.18~-1.64 m降为2.11~-1.56 m,说明TMD对塔顶前后位移影响不大;塔顶侧向位移从0.22~-0.32 m降至0.18~-0.3 m,降幅达21.4%,标准差从0.08降至0.04,说明塔顶侧向运动稳定性得到提高。这是因为塔架侧向运动主要是由湍流风与尾流中的漩涡共同作用引起的,由于TMD控制系统为动力减振装置,故对脉动风载荷引起的动力响应有更好的控制效果。
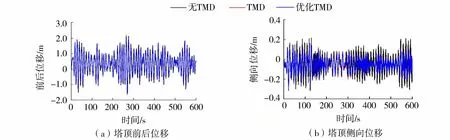
图8 塔顶部位移时域Fig.8 Tower top displacement in time domain
4.3 TMD对塔架根部动力响应的影响
由图9可知:TMD对塔架根部剪力与弯矩均有显著影响;在配置优化TMD时,塔架根部前后剪力从4 464~-3 771 kN降至4 261~-3 538 kN,降幅为9.5%;塔架根部前后弯矩从357 100~-280 500 kN·m降至343 700 ~-265 500 kN·m,降幅仅为3.9%,可知TMD对塔架根部纵向载荷影响不大。塔架根部侧向剪力从614~-690 kN降至503~-667 kN,降幅达22.1%;塔架根部侧向弯矩从58 460~-46 190 kN·m降至56 120~-28 620 kN·m,降幅达8.4%。这是因为浮式风力机顺风向的运动主要为静力响应,而由湍流风和尾流造成的侧向运动属于动力响应。由于TMD控制系统为动力减振装置,故对动力响应有更好的控制效果。

图9 塔基载荷时域Fig.9 Tower root load in time domain
4.4 算例验证
为验证优化结果的可靠性,选取北太平洋实测海况统计数据[20]中出现概率最高的5种海况对TMD优化前后浮式风力机进行计算。海况数据见表1。由结果可知,TMD主要影响横摇、塔架根部侧向位移与载荷。故仅对这4个参数的时间序列进行快速傅里叶变换,得到频域分析结果,如图10所示。

表1 海况数据Table 1 Sea state data

图10 风力机运动响应频域Fig.10 Motion response of wind turbine in frequency domain
通过对比有无优化TMD的浮式风力机在实测海况高频区间中频域运动响应可知:浮式风力机运动主要集中在波频为0.07~0.11 Hz的区间内;随着海况愈发恶劣,浮式风力机运动响应的峰值逐渐变大;配置优化后TMD的浮式风力机相较于配置未优化TMD的浮式风力机,波频内的响应幅值明显降低。5种海况下,峰值频率处的塔顶侧向位移分别降低1.8%、24.3%、27.8%、17.7%、19.6%;峰值频率处的横摇分别降低2.7%、27.0%、19.8%、28.1%、33.3%;峰值频率处的塔架根部侧向剪力分别降低8.0%、24.4%、27.0%、21.9%、24.4%;峰值频率处的塔架根部侧向弯矩分别降低10.5%、24.2%、27.5%、19.7%、21.7%。说明优化后的TMD在大部分海况下可以更好地吸收风力机运动产生的能量,对浮式风力机运动响应的抑制效果优于未优化TMD。在恶劣海况下,控制效果更加明显。
5 结 论
本文以NREL开发的5MW Barge风力机为研究对象,在机舱中配置TMD对浮式风力机运动响应进行控制,利用Kaimal风谱计算湍流风,PM波浪谱生成波浪载荷。考虑风浪耦合作用,基于FAST仿真模拟浮式风力机运动响应。此外,基于遗传算法对TMD结构参数进行优化,得到各参数最优组合,并基于5种实测海况对优化后的TMD进行了合理性与可靠性验证。根据计算结果,得到以下结论:
a.以遗传算法为基础,对TMD系统的质量、刚度与阻尼参数进行了优化,得到各结构参数的最优组合为质量20 902 kg、刚度8 374 N/m、阻尼22 830 N·s/m。
b.由于TMD自振频率更接近于风力机转动频率且仅在水平方向运动,故TMD对浮式风力机的6自由度运动控制主要体现在对横摇、纵摇与首摇的抑制方面。其中,TMD对横摇的控制效果最明显。
c.湍流风载荷中包括静力作用与动力作用两个方面。浮式风力机顺风向的运动主要为静力响应,而由湍流风和尾流造成的侧向运动属于动力响应。由于TMD控制系统为动力减振装置,故对动力响应有更好的控制效果。所以TMD对塔顶侧向位移与载荷的控制效果更加明显。
d.在实际海况中,优化后TMD控制效果明显优于未优化TMD,可以明显降低浮式风力机运动高频区间内的幅度,适用于90%以上的海况。同时随着海况等级的提高,优化后的TMD控制效果更加明显。

