随机矩阵理论和主成分分析融合的滚动轴承性能退化评估方法

朱文昌,罗梦婷,倪广县,王恒

(南通大学机械工程学院,226019,江苏南通)

滚动轴承作为旋转机械的核心部件对旋转设备的可靠运行起着关键作用[1]。对轴承的早期故障检测与性能退化评估,能够有效避免故障发生,减少因设备失效带来的损失,对安全生产具有重要的意义[2],是近年来机械故障诊断领域研究的热点。

在对滚动轴承进行性能退化评估过程中,退化指标的构造非常重要。退化指标应具有如下特点:①能够准确地表征滚动轴承全寿命历程中的不同运行状态;②具有较好的泛化性、单调性能够适应不同工况。Boskoski等基于Jensen-Shannon散度指标评估小波包变换中各小波包的相关关系[3];夏均忠等利用应用累积和对Jensen-Renyi散度指标进行改进,提高了指标的稳定性及单调性[4];尹爱军等通过同步抽取变换对滚动轴承振动信号进行时频分析以获得能量更加集中的时频图,采用复小波结构相似性对时频图的评估值作为滚动轴承性能退化指标[5]。以上方法可对滚动轴承退化状态进行表征,但对轴承早期微弱故障不敏感,对其全寿命历程中的不同运行阶段刻画不精确。Jiang等利用干扰属性投影(NAP)可准确提取轴承退化状态特征,结合隐马尔可夫模型(HMM)较高的辨别力,较好地反映了轴承性能的退化过程,但HMM参数训练中的初始状态数都是依据传统经验设定[6];李玉庆等提取不同磨损量标准试件的振动特征,进行曲线拟合,建立损伤严重程度评估标准曲线作为损伤程度的评估标准,可精确评估轴承的损伤程度,但此方法目前仅在实验室条件下准确率较高[7]。上述方法在轴承状态刻画准确度方面有较大的突破,但在实际工况下的适用性还有待提高。

对轴承信息进行实时采集与分析可实现设备状态的准确监测。然而,监测数据量过大产生的维度灾难对特征提取造成困难,同时采用传统特征提取方法忽略了数据间整体的关联性,易造成信息损失。因此,如何在大数据背景下对轴承状态进行有效评估就成为一个难题。随机矩阵理论作为统计分析的重要数学工具之一,常用于研究大维数据下的渐进分布,已在频谱感知、电网配电、金融统计等领域得到了成功应用。许炜阳等将随机矩阵中的渐进谱理论结合多用户协作检测,提出一种精确的最大最小特征值差的协作感知算法,获得了更好的检测性能[8];安然等将随机矩阵理论中的单环定理应用于电网的无功优化,通过构造无功优化随机矩阵的方式来提取数据特征,实现定量描述某时刻系统状态信息的目的[9];倪广县等基于随机矩阵理论中的M-P定律,提出一种基于最大最小特征值之比的滚动轴承异常检测指标,与传统方法相比可提早检测出异常发生[10]。以上方法皆在大数据分析领域取得良好的应用效果,但只采用单一指标,未将单环定理与M-P律中的多指标充分利用,对数据信息表征不充分。主成分分析(PCA)算法旨在研究数据的内在联系,可将同一空间中的多个指标进行转换融合,融合后的综合指标中少数几个主成分可涵盖多指标绝大部分特征,可更好地对数据信息进行表征,目前已在数据降维、降噪等方面得到广泛应用[11]。

本文基于随机矩阵理论对滚动轴承监测数据协方差矩阵进行特征提取,构造多维特征指标,并结合PCA良好的数据融合性能,提出一种新的融合特征指标用于滚动轴承性能退化评估,应用结果表明了该方法的有效性和可行性。

1 基于随机矩阵理论的滚动轴承多维特征建立

1.1 滚动轴承健康监测矩阵构造

设轴承健康监测数据维数为N、监测时间为T、监测节点数为M,在采样时刻ti,设备第j个节点(如测点)所监测的第n个运行状态特征量定义为监测数据子空间rjn(ti)。对节点j而言,监测的所有N个特征量可以构成一个列向量,即

rj(ti)=[rj1,rj2,…,rjN]T

(1)

将不同采样时刻的监测数据按照时间顺序排列,构成一个数据源矩阵

R=[rj(t1),rj(t2),…,rj(ti),…],j=1,2,…,M

(2)

式中:R即为对滚动轴承监测所得的数据源矩阵。

为了对特定时刻的数据进行实时分析,采用时间窗方法对时间区间参数进行设定,在数据源矩阵R中锁定轴承特定时间段的数据信息。设时间窗口的规模为N×W,则在采样时刻ti,对节点j构成矩阵

Rj(ti)=[rj(ti-W+1),rj(ti-W+2),…,rj(ti)]

i=1,2,…,K;j=1,2,…,M

(3)

将ti时刻平移时间窗锁定的N×W个数据进行规模重构,最终得到特征矩阵Xi∈Cp×q。

1.2 基于随机矩阵的滚动轴承退化特征提取

(4)

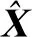
(5)

式中:上标H表示共轭转置;U为Haar酉矩阵。

(6)

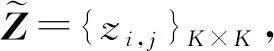
(7)

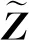
(8)

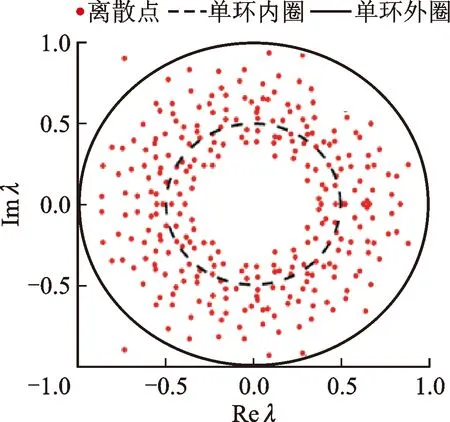
(a)正常状态

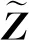
(9)

1.2.2 基于M-P律的矩阵特征提取 将1.1节中ti时刻所构造出的特征矩阵Xi通过式(10)得到其协方差矩阵Bn

(10)

式中:σ2为ti时刻特征矩阵Xi的方差;q为矩阵Xi的列数。

当特征矩阵Xi内元素满足独立同分布,各元素满足均值为0、方差为σ2,p和q趋于无穷,且其行列式之比c=p/q(c∈(0,1])保持不变时,其协方差矩阵Bn特征值的经验谱分布满足M-P定律[14],所有特征值λ满足

(11)

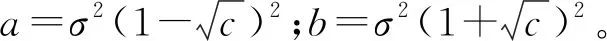
提取协方差矩阵Bn所有的特征值λ。由M-P律可知,Bn的特征值具有收敛性,λ分布在区间S=[a,b]内[15]。基于M-P定律研究协方差矩阵特征值的分布特性,借鉴不同特征指标在频谱感知方面呈现出的良好应用效果[16],最终构建出节点j在采样时刻ti时的12个指标,如表1所示。其中,λmin为协方差矩阵Bn的最小特征值,λmax为最大特征值,λvar为特征值方差,λmid为特征值中位数,tr(·)为矩阵的迹。

表1 基于随机矩阵的特征指标构造公式

2 基于PCA的滚动轴承性能退化特征指标融合

节点j在采样时刻ti时,共提取14个退化特征指标,构成一行向量,如式(12)所示

pj(ti)=[pj,1,pj,2,…,pj,14]

(12)

将不同采样时刻节点j采集到的特征值指标按照时间顺序构成一个多指标矩阵P

P=[pj(t1),pj(t2),…,pj(ti),…]

(13)

本文构建出的多指标矩阵P与单一指标相比,所涵盖的退化信息更全面,但会增加数据的复杂性和冗余度。为实现对信息的综合利用,采用PCA算法对多指标进行主成分提取与信息融合。PCA作为一种数据降维、降噪工具[17],其算法原理是把高维上的多个指标通过坐标转换成新的多元信息融合的综合指标,使得综合指标中少数几个主成分涵盖多个指标的绝大部分信息,不仅降低了数据的冗余度,而且达到了数据综合利用的目的。具体实施步骤如下。

F=[IMF,1,IMF,2,…,IMF,14]

(14)

式中:IMF,i(i=1,2,3,…,14)为融合后第i个特征根对应主成分数据。

步骤3:根据特征根计算各主成分的贡献率CRate(li),贡献率越大即数据融合效果越好。

(15)

步骤4:将各主成分的贡献率相加计算其累积贡献率,将累积贡献率大于90%的主成分IMF,i提取出来,用其平均值构建出融合特征指标pf,通过观察融合指标pf在不同运行阶段的变化上升趋势,对轴承的退化程度进行评估。

本文利用滚动轴承健康监测数据,基于随机矩阵理论构造多维退化特征,并通过PCA建立融合特征指标,实现对其性能退化定量评估,算法流程如图2所示。

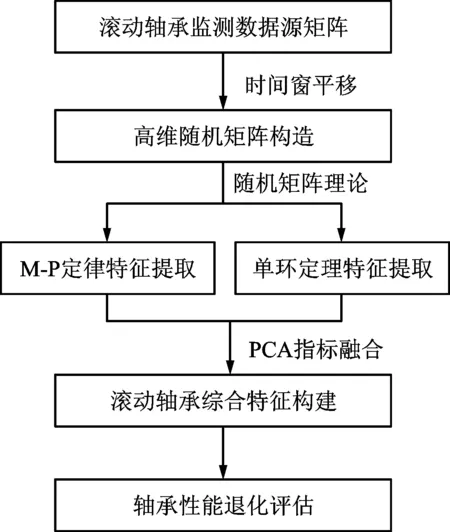
图2 滚动轴承性能退化融合指标构建算法流程图

3 应用研究

3.1 数据来源

本文数据来源于辛辛那提大学智能维护系统(IMS)中心的滚动轴承全寿命试验数据库,4个型号为ZA-2115的双列滚子轴承布置在同一主轴上,轴承径向施加2 722 kg恒定载荷,电机转速为2 000 r/min。试验共经历163.833 h,轴承1外圈发生故障完全失效时结束试验。由于振动信号对轴承内外圈故障较为敏感,故采用加速度传感器每10 min对轴承振动信号进行一次采集,采样频率为20 kHz,共采集数据文件984组。本文采用轴承1数据进行分析与研究。

对轴承1数据根据式(2)构造出监测数据源矩阵R∈C20 480×984,利用1.1节所述平移时间窗对轴承数据进行矩阵构建,实现监测矩阵R中锁定特定时空断面的数据信息。平移时间窗规模为Q∈C20 000×10,对监测数据进行锁定并进行特征矩阵构造,在采样时刻ti时,节点j构成特征矩阵Xi∈C400×500,分析其协方差矩阵特征值λ的概率密度分布F(λ),如图3所示。由图3可见:在轴承正常状态,其特征值整体分布有良好的渐进收敛特性,符合M-P定律(如图3a所示);随着轴承进入退化状态,特征值逐渐发散且整体呈增大的趋势,分布特性逐渐被破坏(如图3b、c所示)。故可用M-P律对轴承特征值分布进行研究,在滚动轴承处于正常状态,其特征值整体分布收敛且稳定,可使得特征值指标变化呈现为一条稳定直线。当进入异常状态,特征值分布发生变化,整体有变大的趋势,特征值指标随着退化的加剧而变化剧烈,可研究特征值收敛与发散实现对轴承正常与异常状态的区分,且通过对特征值整体的变化对轴承退化程度进行有效表征。

(a)正常状态

3.2 轴承1退化融合特征指标构建

基于随机理论中的单环定理与M-P律对不同采样时刻所构造出的矩阵Xi进行特征指标提取,构造出14个无量纲特征指标,其幅值随时间的变化趋势如图4所示。

由图4可知:14个特征指标反映了轴承1由正常到失效整个全寿命历程,各指标都呈现了一定趋势,但对早期异常敏感程度、轴承各阶段划分的准确度及指标单调性方面均未达到最佳,指标p1、p2对轴承早期微弱故障较为敏感,但整体单调性差,对轴承各退化阶段开始与结束表征不准确;p3、p6、p13指标有较好的单调性,但在轴承退化加剧时所呈现出的变化趋势不明显;其余指标对轴承的退化过程反映较为剧烈,但数据存在冗余,总体上这14个指标所含信息较为嘈杂,难以对轴承性能退化过程进行很好的表征。因此,需要对不同指标进行主成分分析,降低冗余特征对退化指标的干扰,同时保留这14个指标中所需要的有效信息构造出一个融合指标用于对轴承退化历程进行表征。在对14个特征值指标按照第2节所示方法进行PCA融合后,计算各成分特征根数及其累计贡献率,如表2所示。可以观察到,融合后前3组主成分的贡献率较大,其累计贡献率已达到93.61%(大于90%),融合效果较好,在保证最少主成分的前提下基本可涵盖轴承14个指标中所有有用信息,故选取前3组主成分,利用其均值构建出融合特征指标pf用于对轴承退化历程描述和状态识别。

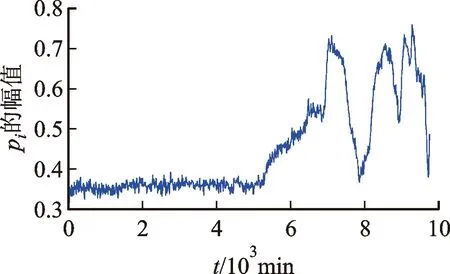
(a)指标p1变化趋势

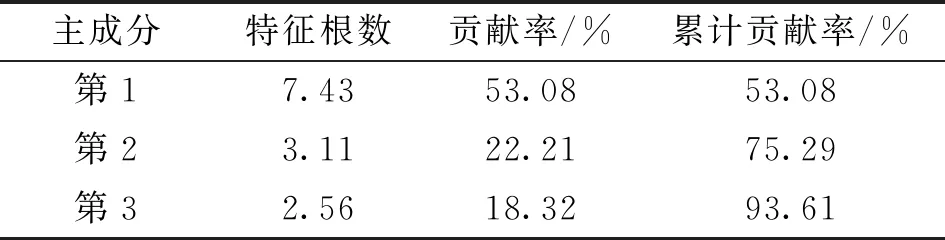
表2 轴承1退化特征主成分分析结果

3.3 轴承1早期异常状态检测

图5 本文基于PCA融合特征指标的轴承1早期异常检测

通过PCA处理后获得融合指标pf对轴承1进行性能退化评估,结果如图5所示,通过PCA坐标变换使得各个特征指标样本部分散落于新坐标轴的负半轴,使其纵坐标出现负值,但指标整体的单调性、对早期异常检测的灵敏度与退化历程的表征能力较各单一指标而言有所加强。由图5可见,该指标在5 230 min前变化平缓、波动较小,之后上升明显,据此判断轴承1的早期异常出现在5 230 min。为验证PCA融合特征指标对滚动轴承早期异常点的敏感程度,将检测结果与其他算法进行对比。文献[10]利用最大最小特征值之比(α=λmax/λmin)指标对轴承1进行早期异常点检测,结果如图6所示,较传统峭度指标可提前11 h检测出轴承异常的发生,但此方法通过对轴承信号进行频域、时域特征的提取,破坏了数据整体的关联性,造成部分有用信息损失,且单一特征值指标对轴承退化信息表征不完整,使其未能及时检测出轴承的早期异常。对比图5、图6可知,PCA融合特征指标比文献[10]采用最大最小特征值之比指标提前了12.5 h检测出轴承1的早期异常,验证了本文方法对轴承早期故障更为敏感。

将轴承1早期异常点后融合指标变化趋势与图6所示单一指标相比,当轴承退化过程中承受冲击时,融合特征指标变化趋势更为平滑,证明采用平移时间窗建立出的特征指标,可降低数据频繁波动对整体趋势变化产生的干扰,有效提高了指标的稳定性。

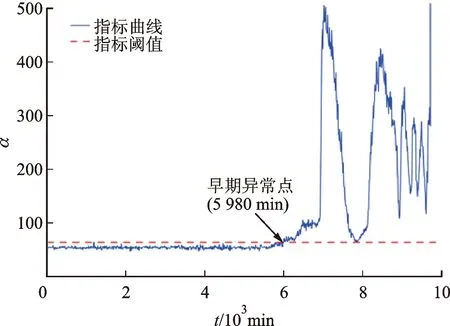
图6 文献[10]基于最大最小特征值之比算法的轴承1早期异常检测

3.4 轴承1性能退化评估

利用PCA融合特征指标对轴承1运行状态进行划分和性能评估,如图7所示,采用传统方法对退化指标曲线的变化趋势与变化幅度分析进而对轴承退化状态进行划分,在5 230 min之前为正常状态;5 230 min后,轴承1开始进入不同程度的退化状态。5 230～6 260 min为早期退化状态,此阶段性能指标有明显的上升趋势;6 260～7 880 min与7 880～9 320 min分别表征中期和严重退化状态,轴承1的指标曲线存在明显的周期性波动;9 320 min时为轴承的严重故障点,此后指标急剧上升,意味着轴承1进入故障状态并即将失效。为验证本文方法的有效性,与文献[18]中基于HDP-CHMM算法得到的性能退化评估结果进行比较,HDP-CHMM算法获得的早期异常点为5 760 min,严重故障点为9 300 min,与本文方法的结果接近。因此,可证明融合特征指标对轴承1全寿命历程中的不同运行状态可进行有效表征。

图7 本文基于随机矩阵融合指标的轴承1性能退化评估结果

考虑到数据变化的不稳定性,传统方法过多依赖退化指标变化的趋势与幅度,使得轴承状态划分缺少科学性。本文结合轴承故障机理与故障频域信息对轴承1状态识别与划分的有效性进行分析,降低了仅依据轴承数据变化趋势导致状态划分不准确的风险。课题组前期研究结果表明[19],轴承1的早期异常为外圈早期故障,当轴承1进入中期退化状态,此时外圈表面缺陷刚刚形成,小的剥落或者裂纹出现,振动幅值上升,随后滚动体连续运转将缺陷抚平,幅值又会下降,融合指标呈现周期性变化,此现象被称为愈合现象[20]。如图7所示,融合指标曲线在6 260 min后开始下降,进入波动状态,此波动一直持续到9 320 min,此期间存在两个变化趋势较相似的波动周期(6 260～7 880 min与7 880～9 320 min),且在7 880～9 320 min中融合特征的幅值较上一阶段有所增加,表明轴承损伤进一步加剧。因此,将这两个周期分别确定为轴承1的中期与严重退化阶段,此阶段中融合指标所呈现出的变化能反映轴承外圈的故障发展历程;在9 320 min后,轴承损伤扩展到更广的区域而无法愈合,振动不断加剧,轴承发生故障,即将完全失效。

分别提取轴承1早期退化状态(5 230～6 260 min)、中期和严重退化状态(6 260～9 320 min)的振动数据进行频谱分析,如图8a所示,当滚动轴承开始退化时,受故障频率影响,产生幅值较大的频率成分f0=985.4 Hz,约为外圈故障频率fe(236.73 Hz)的4倍,但早期退化状态时其高频段幅值较小;当进入中期和严重退化状态后,高频段的幅值较前一阶段有较大的增长,频谱图高频段出现了如图8b所示的等间隔边频带Δf=231 Hz(接近外圈故障特征频率)。结合轴承故障机理分析,轴承1在此阶段经历了“损伤-愈合-再损伤”的过程,性能退化加剧,滚动体与外圈频繁冲击,瞬态冲击能量较大,激励起轴承1的固有频率(5 172 Hz)并出现调制现象,产生了以轴承固有频率为中心频率、以外圈故障频率为调制频率的边频带。在运行了9 320 min后,轴承1损伤严重无法愈合。因此,本文提出的融合指标对轴承1中期和严重退化状态的划分和评估,实现了对其经历的两次“损伤-愈合-再损伤”变化过程的描述,较为精准地描述了轴承1的实际退化历程。

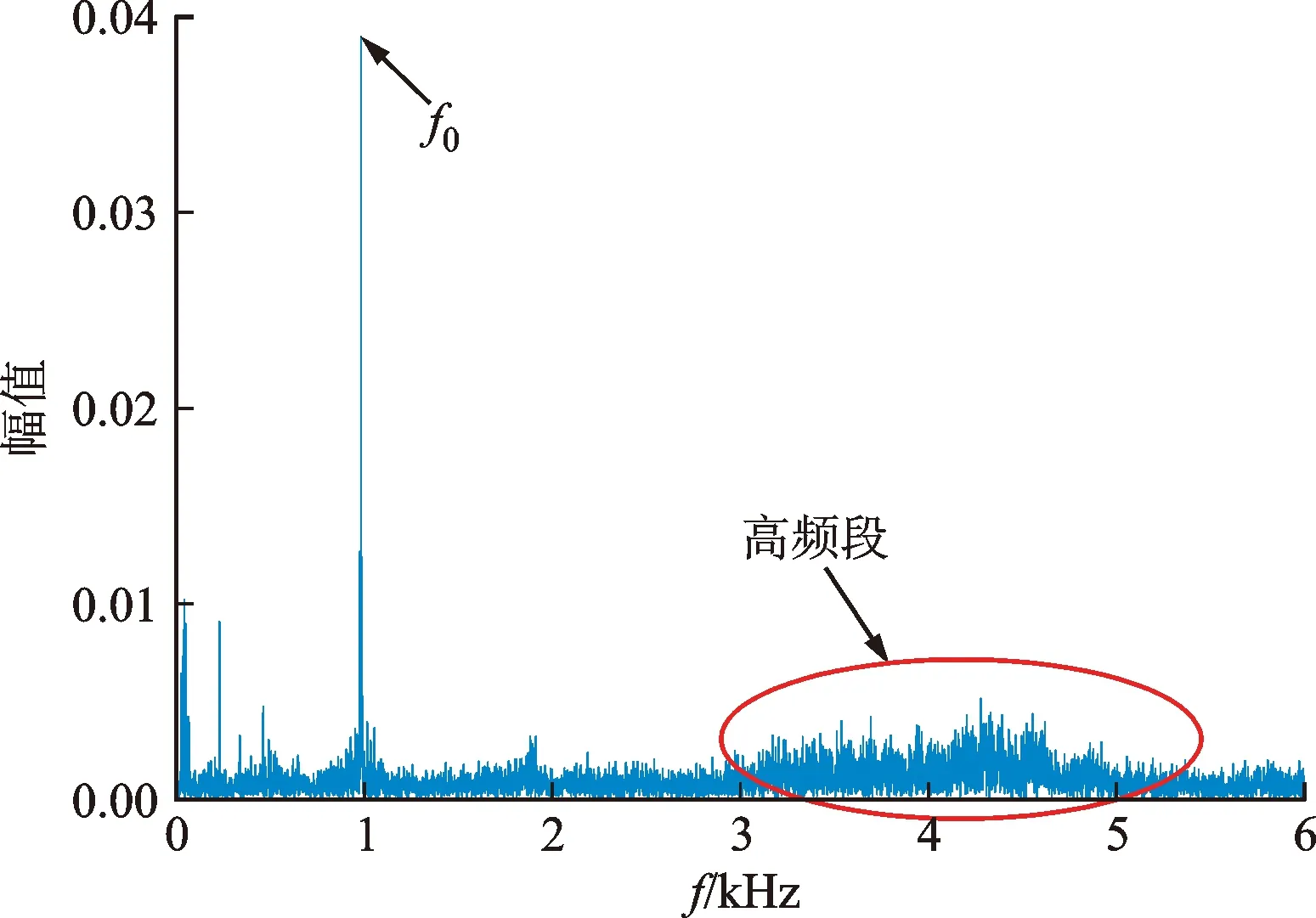
(a)早期退化状态

4 结 论

(1)利用平移时间窗对监测数据源矩阵不同时间段的数据进行锁定采集,构造出的矩阵包含当前时刻信息与历史信息,降低了因数据频繁波动而对整体趋势变化产生的干扰,提高了退化指标的稳定性。

(2)利用IMS轴承寿命数据,对滚动轴承1研究结果表明,本文融合特征指标比最大最小特征值指标可提前12.5 h检测出轴承早期异常的发生;通过与HDP-CHMM算法检测出的早期异常点与严重故障点进行比较,证明了融合特征指标可对轴承的退化历程进行有效评估,为设备的退化评估程度提供了一种可行的量化指标;结合轴承1的故障机理与轴承故障信号的频域分析,验证了基于融合特征指标划分轴承全寿命运行状态的有效性和合理性。

(3)本文所提出的方法可实现对滚动轴承性能退化历程的有效评估,通过数据变化研究了轴承失效过程和失效机理,但未能结合具体试验与材料组织变化进行深入探究,在后续工作中将针对此不足开展相关试验,做进一步研究。