利用回波时频相关差异的雷达欺骗干扰识别方法
张亮,王国宏,杨志国,张翔宇,李思文
(1.海军航空大学信息融合研究所,264001,山东烟台;2.中国人民解放军94326部队,250000,济南;3.空军参谋部,100032,北京)
线性调频(LFM)信号是雷达常用信号形式之一,对LFM雷达的干扰通常包括压制式干扰和欺骗式干扰。压制式干扰无需雷达脉冲重复频率、信号带宽等先验信息,侧重依靠高的干扰功率压制雷达系统,但随着脉冲压缩、相参积累等技术的应用,传统噪声干扰压制效能受到显著削弱,而欺骗式干扰追求制造高逼真虚假目标,以较低的干扰功率达成欺骗干扰效果。LFM具有距离-多普勒耦合特征,该特征能够使雷达对目标多普勒具备高的容许度,但同时也容易遭受转发式干扰攻击,移频干扰(FSJ)就是针对该特征的新型欺骗干扰[1],典型样式包括单分量FSJ、多分量FSJ[2-4]及众多的改进形式[5-7],常用于自卫式干扰场景下[8-11]。为对抗自卫式FSJ,文献[8]利用干扰机不可避免的转发时延,通过参数估计设计参考信号,根据参考信号与延迟回波相关峰值偏移识别真假目标,但该方法无法对抗多分量FSJ。针对该问题,文献[9]利用FSJ假目标导前或滞后距离与雷达发射信号调频斜率呈反比关系特点,设计调频斜率捷变LFM(SV-LFM)识别真假目标,但SV-LFM波形不可避免会增加发射机复杂度。针对常规LFM雷达,文献[10]利用分数阶傅里叶变换(FRFT)时频旋转特性分离真实回波和干扰信号,通过测量中心频率识别信号类型。文献[11]同样基于中心频率测量,但未使用FRFT,而是通过正交极化辅助天线扩展接收通道,利用盲源分离算法进行信号分离。文献[10-11]可同时对抗单分量FSJ和多分量FSJ,但FRFT及盲源分离算法计算量较大。
针对上述问题,本文以LFM相参雷达抗自卫式欺骗干扰为背景,利用雷达回波时频相关差异,提出经典时频相关移频干扰识别方法和尺度时频相关移频干扰识别方法,根据不同处理方式下目标对应关系取峰值差,对比门限识别真假目标。试验结果表明,所提2种方法低虚警率前提下,均能保持较高的干扰识别准确率,对比分析进一步验证算法效能。
1 FSJ干扰特性
雷达发射LFM脉冲信号,零中频复数形式为
s(t)=rect(t/Tp)eiπkt2
(1)
式中:t为时间;Tp为脉宽;k=B/Tp为调频斜率,B为信号带宽。多分量FSJ时域表示式为
(2)
式中:L为分量个数;jl(t)为j(t)的第l个分量;fl为第l个分量移频量;当L=1时,j(t)退化为单分量FSJ。设自卫式干扰机为点目标,目标的初始距离为Rt、径向速度为vt,则1个相干处理间隔(CPI)内雷达接收真实回波基带信号为
sr(tf,tm)=σs[tf-2R(tm)/c]e-i4πR(tm)/λ
(3)
式中:tf为快时间;tm=mTr为慢时间;Tr为脉冲重复周期;σ为反射系数;R(tm)=Rt-vttm为目标与雷达径向距离函数;c为光速;λ为波长。雷达接收多分量FSJ为
(4)
式中:Al为第l个分量幅度。假设真实目标未发生距离走动,fl(tm)=fl,雷达接收受干扰回波为
xr(tf,tm)=e-i4πRt/λσs(tf-t0)ei2πfdtm+
(5)
式中:w(tf,tm)为高斯白噪声;fd=2vt/λ为干扰机多普勒频率;t0=2Rt/c为不考虑慢时间影响回波时延。对xr(tf,tm)进行脉冲压缩,得到受干扰回波、真实回波和第l个干扰分量脉冲压缩结果分别为
(6)
ys(tf,tm)≈e-i4πRt/λσTpsinc[πB(tf-t0)]ei2πfdtm
(7)
yl(tf,tm)≈e-i4πRt/λAl(Tp-|fl|/k)ei2πfdtm·
sinc[π(B-|fl|)(tf-t0+fl/k)]eiπfl(tf-t0)
(8)
式中:yr(tf,tm)、ys(tf,tm)、yl(tf,tm)和yw(tf,tm)分别为脉冲压缩后的受干扰回波、真实回波、第l个干扰分量和噪声;sinc(·)为未归一化辛格函数。计算yr(tf,tm)慢时间傅里叶变换,得到相参积累结果分别为
yr(tf,fm)=
(9)
ys(tf,fm)≈e-i4πRt/λσTpsinc[πB(tf-t0)]·
Msinc[πMTr(fm-fd)]
(10)
yl(tf,fm)≈e-i4πRt/λeiπfl(tf-t0)Al(Tp-|fl|/k)·
sinc[π(B-|fl|)(tf-t0+fl/k)]·
Msinc[πMTr(fm-fd)]
(11)
式中:yr(tf,fm)、ys(tf,fm)、yl(tf,fm)和yw(tf,fm)分别为脉压相参积累后的受干扰回波、真实回波、第l个干扰分量和噪声;fm为对应多普勒频率。自卫式干扰下,多分量FSJ经脉压相参积累生成L个高逼真虚假目标,假目标导前(滞后)距离与移频量和调频斜率有关。
2 干扰识别原理
2.1 经典时频相关干扰识别方法
脉冲压缩为回波信号与雷达发射信号时域互相关,去斜处理为频域互相关[12]。FSJ初始频率与雷达发射信号不同,其时域相关性不如真实回波,而干扰频谱与发射信号频谱形状相同,但中心频率不同,其频域相关性与真实回波相同。利用回波信号与雷达发射信号的时、频相关差异,可实现干扰鉴别。基于该思路,本文提出一种经典时频相关移频干扰识别方法(本文方法1)。
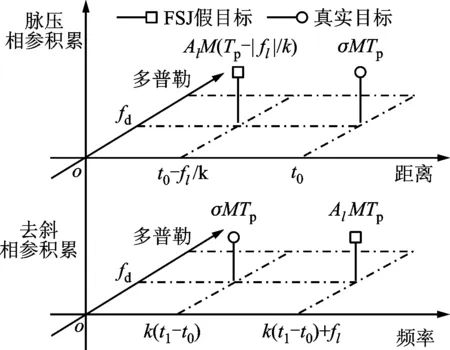
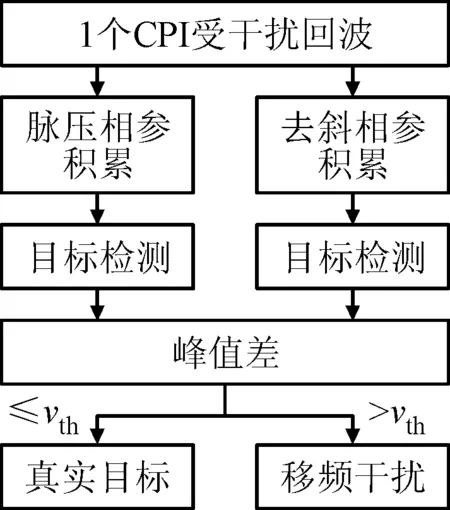
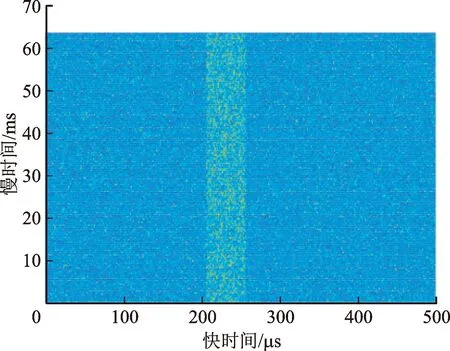
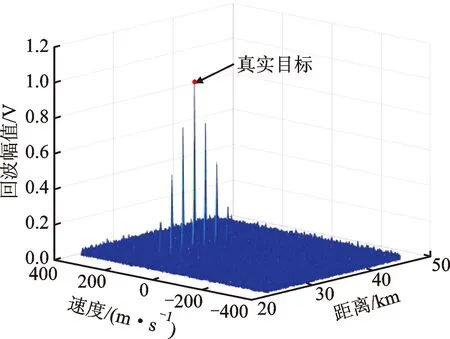
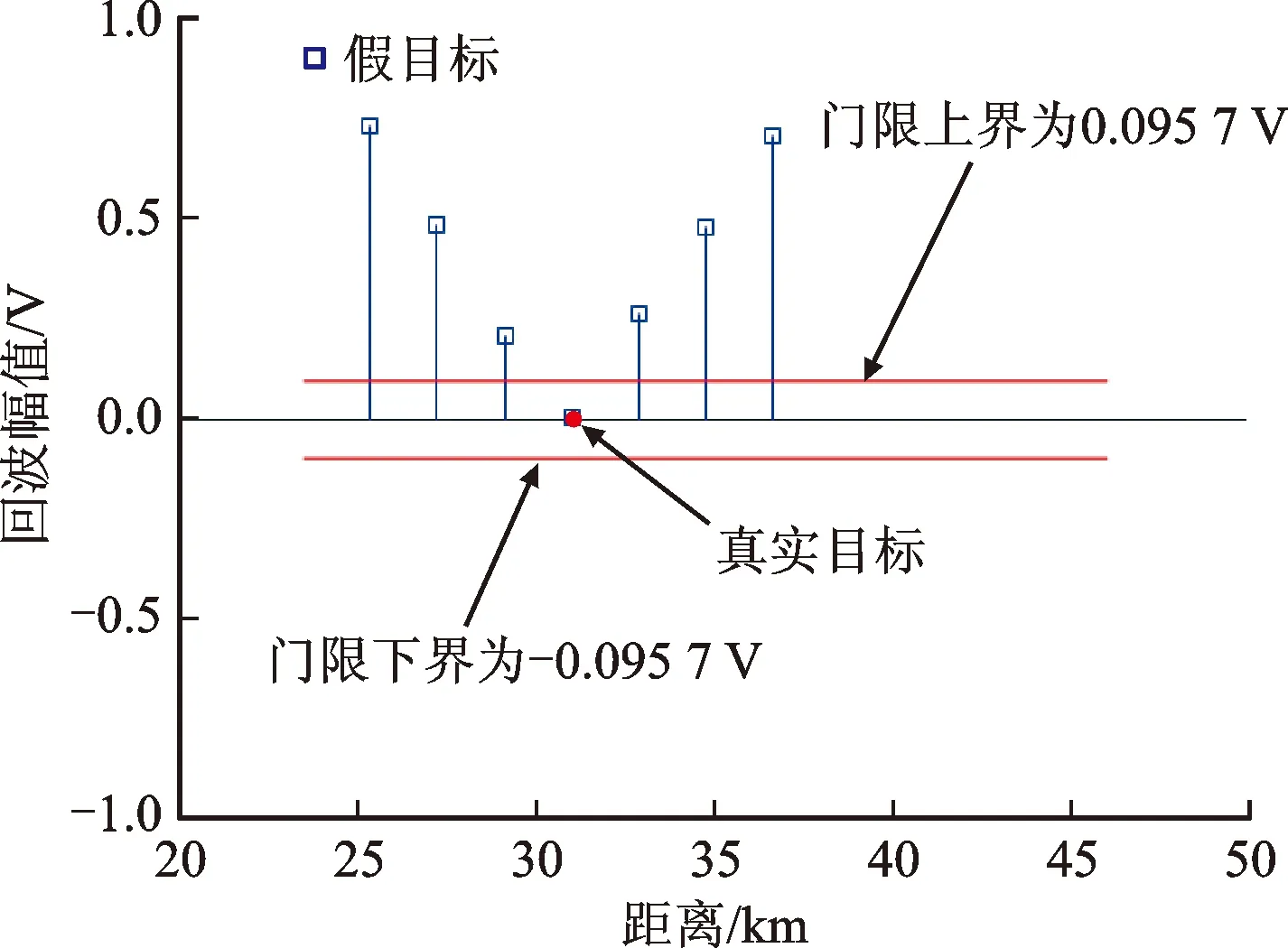
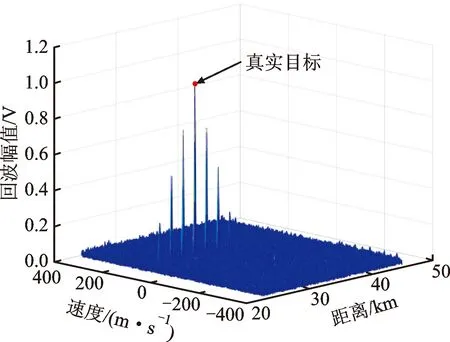
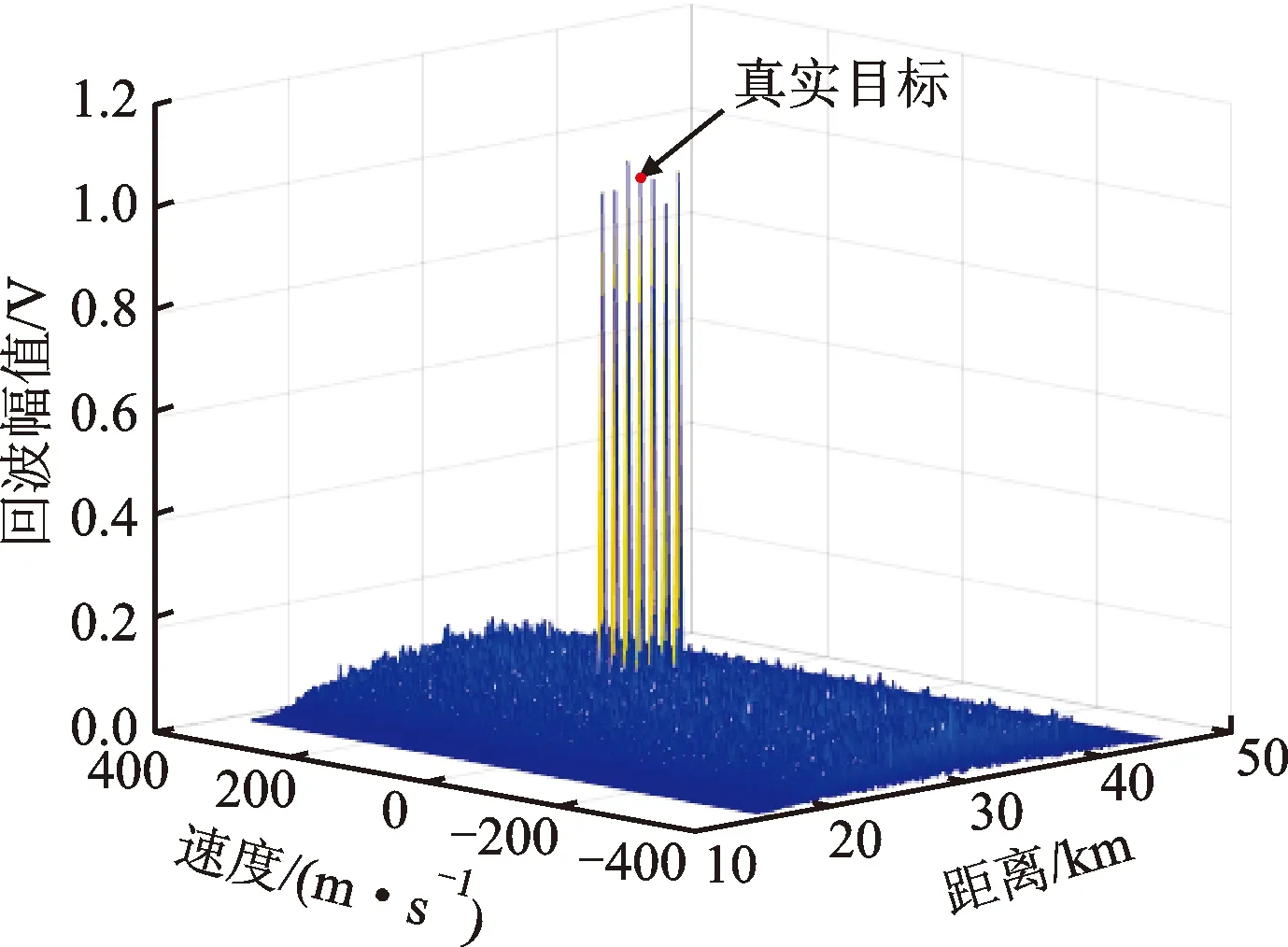
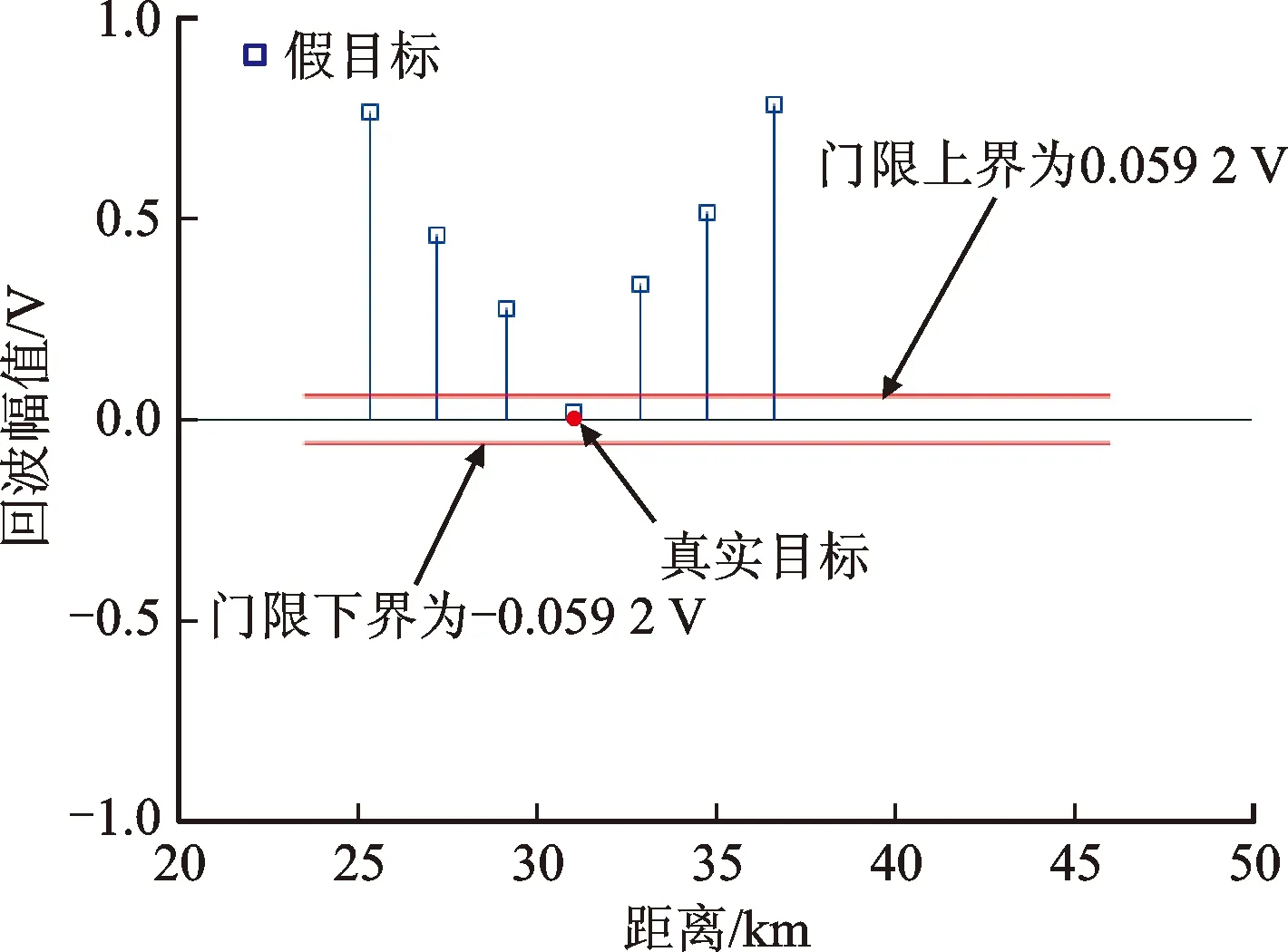
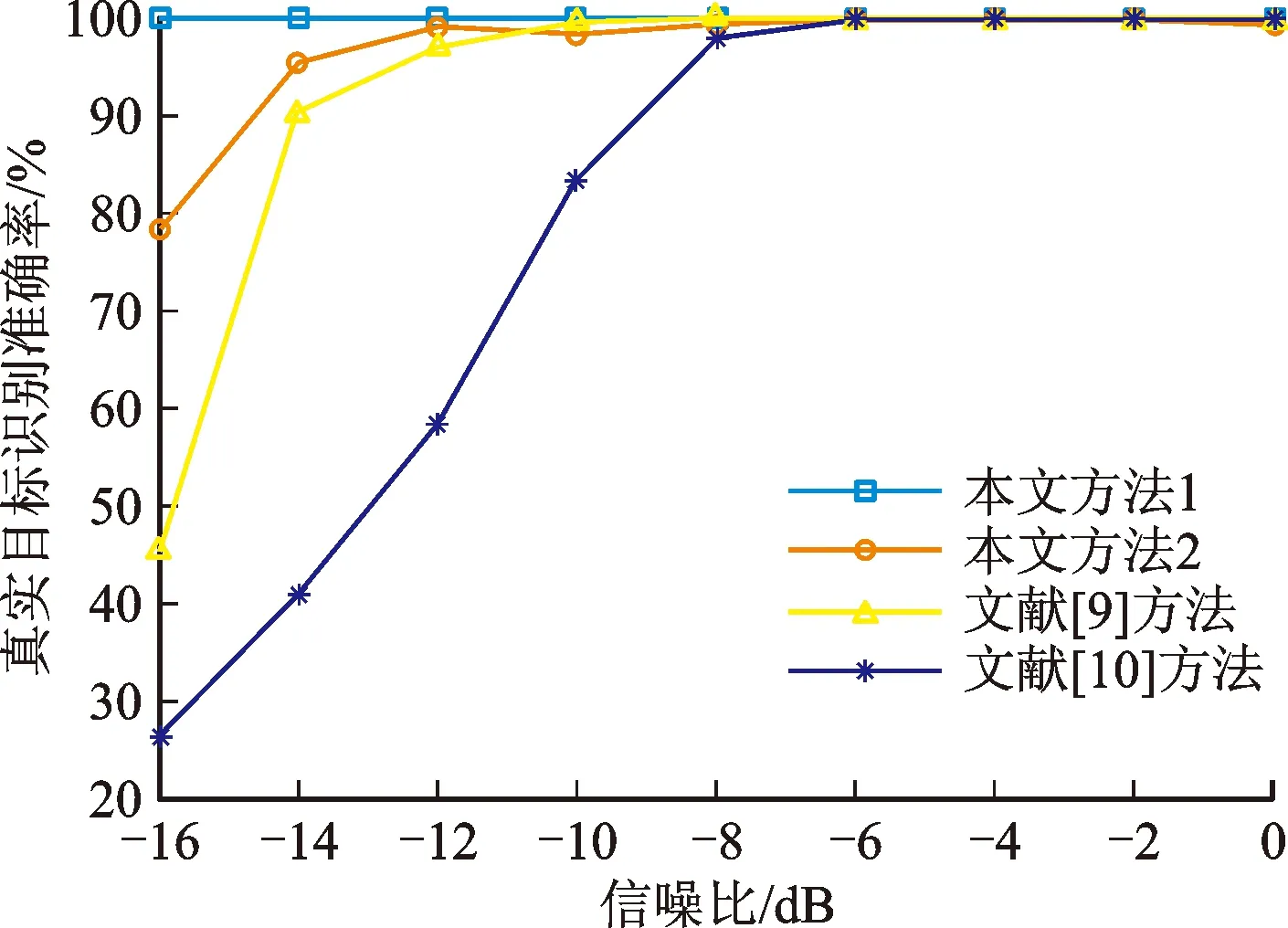
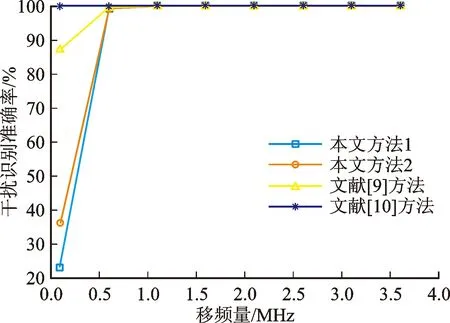
对回波快时间去斜处理,设距离窗覆盖真实回波,距离范围[R1,R2],且R1 win(tf)=rect[(tf-t1)/Tw] (12) 式中:t1=(R1+R2)/c为窗中心;Tw=2(R2-R1)/c为窗宽度。根据距离窗设计参考LFM信号 rstr(tf)=win(tf)e-iπk(tf-t1)2 (13) 利用参考信号对式(5)快时间乘积调制,得到 (14) (15) sinc{πTp[f-k(t1-t0)]}Msinc[πMTr(fm-fd)] (16) AlTpsinc{πTp[f-k(t1-t0)-fl]}· Msinc[πMTr(fm-fd)] (17) (18) 式中:vpc、vdc分别为脉压相参积累、去斜相参积累目标峰值;vth为阈值。 综上分析,图2给出了干扰识别流程。 图1 回波脉压相参积累和去斜相参积累结果示意图 图2 干扰识别流程 回波快时间去斜处理工程实现难度较低,但需设置距离窗以完全覆盖真实回波与干扰信号,窗宽度的选取应确保去斜参考信号、调制后回波满足采样定理[14]。FRFT常用于LFM信号检测,数值计算中无需对信号加距离窗,基于量纲归一化理论的简明分数阶傅里叶变换(CFRFT)是FRFT简化形式之一[15-16],计算量低于Ozaktas采样型离散FRFT[17-18]。本文以CFRFT作为回波处理工具,进一步提出尺度时频相关移频干扰识别方法(本文方法2)。 将CFRFT拓展至二维,容易得到信号x(s,t)的(p1,p2)阶二维简明分数阶傅里叶变换(2D-CFRFT)为 (19) Kp1,p2(s,t,f1,f2)=eiπcotα1s2e-i2πf1seiπcotα2t2e-i2πf2t (20) 式中:f1和f2分别为2D-CFRFT的快时间频率和慢时间频率;Kp1,p2(s,t,f1,f2)为核函数;α1=p1π/2、α2=p2π/2分别为二维旋转角度。根据雷达发射信号调频斜率,确定阶次pk=acot(-k)/(π/2),令p1=pk、p2=1,将式(5)代入式(19)得到回波信号(pk,1)阶的2D-CFRFT为 (21) sinc[πTp(f1-cotαkt0)]sinc[πMTr(f2-fd)] (22) sinc[πTp(f1-cotαkt0-fl)]sinc[πMTr(f2-fd)] (23) 雷达载频400 MHz,脉冲重复频率2 kHz,相参积累个数为128,雷达发射LFM脉冲信号,脉宽为50 μs,带宽为4 MHz,采样频率为16 MHz。设自卫式干扰机为点目标,初始距离为31 km,多普勒频率为250 Hz,多分量FSJ包含6个分量,移频量分别为-3、-2、-1、1、2、3 MHz。 3.2.1 仿真试验1 分析本文方法1(经典时频相关干扰识别方法)的可行性。设信噪比为-10 dB、干信比为0 dB,图3给出了1个CPI受干扰回波。对回波分别进行脉压相参积累和去斜(距离窗为23.5~46 km)相参积累,结果分别如图4、图5所示。可以看出,真实回波峰值差接近于0,干扰峰值差明显大于真实回波峰值差,且两种处理方式下的噪声平均功率不同。对两种处理结果取中位数[19-20],得到噪声平均功率分别为0.018 4 W和0.031 9 W,进而确定干扰鉴别门限为0.095 7 W,结合式(18),图6给出了识别结果,由图6可见,真实目标和6个虚假目标均被有效识别,且未出现误判情况。 图3 采用本文方法1的受干扰回波 图4 采用本文方法1的脉压相参积累结果 图5 采用本文方法1的去斜相参积累结果 图6 采用本文方法1的干扰识别结果 3.2.2 仿真试验2 分析本文方法2(尺度时频相关干扰识别方法)的可行性。信噪比、干信比取值同3.2.1节相同,对一个CPI回波进行脉压相参积累,结果如图7所示,回波2D-CFRFT结果如图8所示。由图7、图8可见,真实目标回波峰值差同样接近于0,干扰峰值差明显大于真实回波峰值差,且两种处理方式下的噪声平均功率大小及分布均不相同。图9给出了采用本文方法2的干扰识别结果,可见真假目标同样被有效识别。 图7 采用本文方法2的脉压相参积累结果 图8 采用本文方法2的2D-CFRFT结果 图9 采用本文方法2的干扰识别结果 为评估本文所提方法的识别效能,定义真实目标识别准确率(TRA)为ATR、干扰识别准确率(JRA)为AJR,虚警率为100-ATR,漏警率为100-AJR。在信噪比取值-16~0 dB、间隔2 dB时,运行蒙特卡罗仿真500次,将本文方法与文献[9]、文献[10]方法进行对比,给出真实目标识别准确率随信噪比变化曲线如图10所示。由图10可以看出,真实目标识别准确率与信噪比近似呈正比关系,当信噪比大于-12 dB时,本文方法的真实目标识别准确率均接近100%,说明算法误判真实目标为假目标的概率较小,而文献[9-10]方法在低信噪比条件下的虚警率明显高于本文方法。 图10 本文方法与文献[9-10]方法的真实目标识别准确率随信噪比变化曲线 图11 本文方法与文献[9-10]方法的干扰识别准确率随干信比变化曲线 同理,信噪比取值-15、-10、-5 dB,干信比取值为-10~20 dB,间隔为2 dB,干扰移频量2 MHz,运行蒙特卡罗仿真500次,图11给出本文及对比方法的干扰识别准确率随干信比变化曲线。可以看出,不同干信比条件下,文献[9-10]方法的干扰识别准确率均接近100%,算法误判假目标为真实目标的概率较小,而本文2种方法的干扰识别准确率接近100%的临界干信比为0 dB,对干信比要求高于文献[9-10],考虑到干扰功率通常大于真实回波功率,因此本文方法对干信比的要求可以接受。 进一步分析干扰移频量对干扰识别准确率的影响。信噪比取值-15、-10、-5 dB,干信比取10 dB,移频量取0.1~3.7 MHz,间隔0.2 MHz,运行蒙特卡罗仿真500次,图12给出了干扰识别准确率随移频量变化曲线。可以看出,移频量对干扰识别准确率影响同样较大,当移频量大于0.6 MHz时,文献[9-10]与所提方法干扰识别准确率均接近100%,当移频量小于0.6 MHz时,漏警率均显著提高。综上分析可知:算法效能同时受信噪比、干信比、干扰移频量的影响;信噪比越高,真实目标识别准确率越高,产生虚警的概率越小;干信比越高,移频量越大,干扰识别准确率越高,发生漏警的概率也越小。文献[9-10]具备较高的干扰识别准确率,但低信噪比条件下易将真实目标误判为假目标,而本文方法在低信噪比条件下虚警率较低,且能保持较高的干扰识别准确率。 图12 本文方法与文献[9-10]方法的干扰识别准确率随移频量变化曲线 脉冲压缩为回波信号与雷达发射信号时域互相关,去斜处理为频域互相关,回波最优阶次分数阶傅里叶变换为尺度化频域互相关。本文利用真实回波、移频干扰与雷达发射信号时频相关差异,提出经典时频相关干扰识别方法和尺度时频相关干扰识别方法。试验结果表明:当干信比大于0 dB、干扰移频量大于雷达发射信号带宽15%时,本文2种方法的干扰识别准确率均接近100%;当信噪比大于-12 dB时,本文方法产生的虚警率均小于1%,优于中心频率测量法和调频斜率捷变法。本文中未涉及移频干扰改进形式,其识别抑制问题后续将做进一步研究。
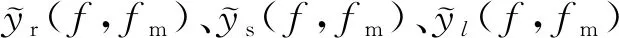
2.2 尺度时频相关干扰识别方法
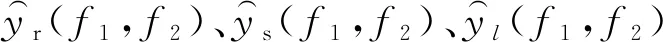
3 仿真实验与结果分析
3.1 参数设置
3.2 算法可行性分析

3.3 算法效能分析

4 结 论

