航空发动机高压转子装配偏心预测和相位优化的智能算法应用研究

张子豪,郭俊康,洪军,孙岩辉

(1.西安交通大学机械工程学院,710049,西安;2.西安交通大学现代设计及转子轴承系统教育部重点实验室,710049,西安;3.长安大学工程机械学院,710064,西安)

航空发动机是一种高度复杂和精密的热力机械,由机械制造各零部件装配而成,其中转子组装是整个装配的核心环节。转子系统转速极高,承受巨大的启动负载以及热冲击,而且伴随大量的、复杂的动态机械载荷作用[1-2]。如果转子系统装配方案设计不合理、装配偏心量过大,整机会产生巨大振动,直接影响发动机服役性能。

高压转子设计为多级组合转子,为减少转子中装配偏心误差,减少装配现场的试装、调试等工作,提高工作效率。其中Hussain通过齐次矩阵变换方法,建立了航空发动机转子连接装配分析模型[3-4],基于该模型预测装配偏心和优化零件的装配相位,以提高整体装配的几何同轴度;文献[5]基于矢量投影方法,提出了一种堆叠装配方法和一种调整方法,旨在准确预测装配偏心;金隼通过雅克比旋量模型建立了航空发动机转子误差传递分析[6-7],以多级盘装配同轴度综合误差最小为目标,优化了装配角度,并且进一步改进模型,考虑止口处的部分并联结构,提高偏心预测准确度。单福平等建立了包含尺寸和形位公差的刚性装配模型[8-9],以蒙特卡洛仿真方法预测航空发动机的装配精度,对零件安装角度进行了优化。

以上方法均是基于刚体假设完成的偏心计算和相位优化,本质是不考虑配合面的形貌特征,忽略装配过程中的受力变形现象。但是,零件在加工制造中必然存在加工误差,装配变形也是不可避免的。为了提高装配偏心预测精度以及计算效率,本文希望以智能算法为核心,提出一种新方法来解决以上问题。

在智能算法应用方面,Prabhaharan提出了基于遗传算法的最优化公差分配算法[10],刘海博等通过粒子群算法建立了公差优化模型[11],王巍等结合了BP神经网络法与评价函数法[12],刘超等将粒子群工具箱作为并行公差优化设计模型的求解工具,进行并行工序公差优化设计[13],Ming等采用人工智能算法进行公差分析[14],张铭鑫等提出了一种集模糊模拟、神经网络和遗传算法相结合的混合智能算法,以求解再制造装配车间调度问题[15]。

受上述工程问题及相关研究启发,本文通过构建人工神经网络模型进行装配偏心预测,再通过粒子群算法进行装配相位的优化。由于神经网络训练需要大量数据,而实验数据很少,故本文通过傅里叶级数和有限元法生成大量网络所需的训练数据,在偏心预测准确的条件下,通过粒子群算法进行相位优化,得出最后装配过程。

1 几何误差表达和数据生成

1.1 基于傅里叶级数的几何误差分解

首先用高精度综合测量机IMAP4,通过AccuScanTMXE400 m-RT系统采集稳定可靠的测量数据,测量过程如图1所示,得到3 600个端向跳动误差数据和径向跳动误差数据,如图2和图3所示。

图1 测量转子配合面

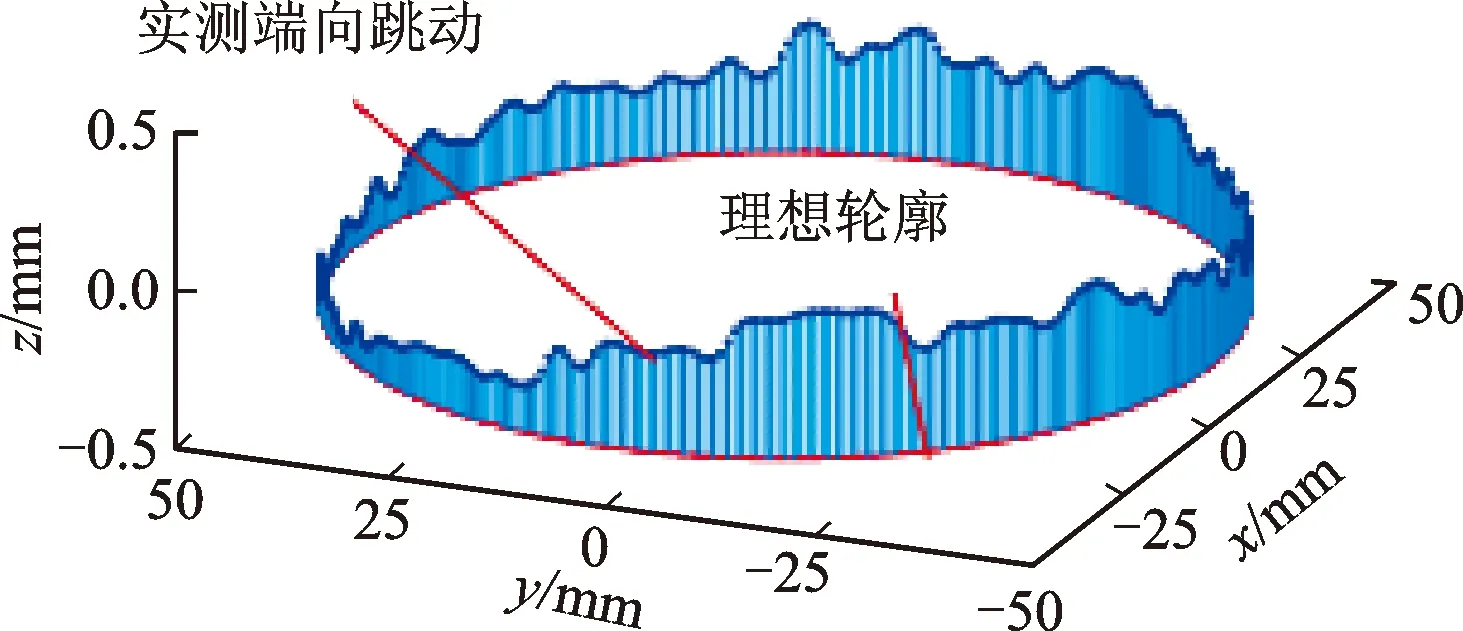
图2 端向跳动误差轮廓[16]

图3 径向跳动误差轮廓[16]

使用傅里叶级数生成模拟随机误差[16],er和ea分别表示径向轮廓轨迹的傅里叶级数和端向跳动轮廓的傅里叶级数表达式。er表达式如下

(1)

式中:akr为径向跳动轮廓傅里叶级数的幅值;kr为径向跳动轮廓傅里叶级数的频率;ykr为径向跳动轮廓傅里叶级数的相位。

ea表达式如下

(2)

式中:aka为端向跳动轮廓傅里叶级数的幅值;ka为端向跳动轮廓傅里叶级数的频率;yka为端向跳动轮廓傅里叶级数的相位。

通过傅里叶变换,径向跳动轮廓误差数据和端向跳动轮廓误差数据主要集中在前30阶傅里叶级数和的形式,如图4和图5所示,因此n取30较为合适[16]。

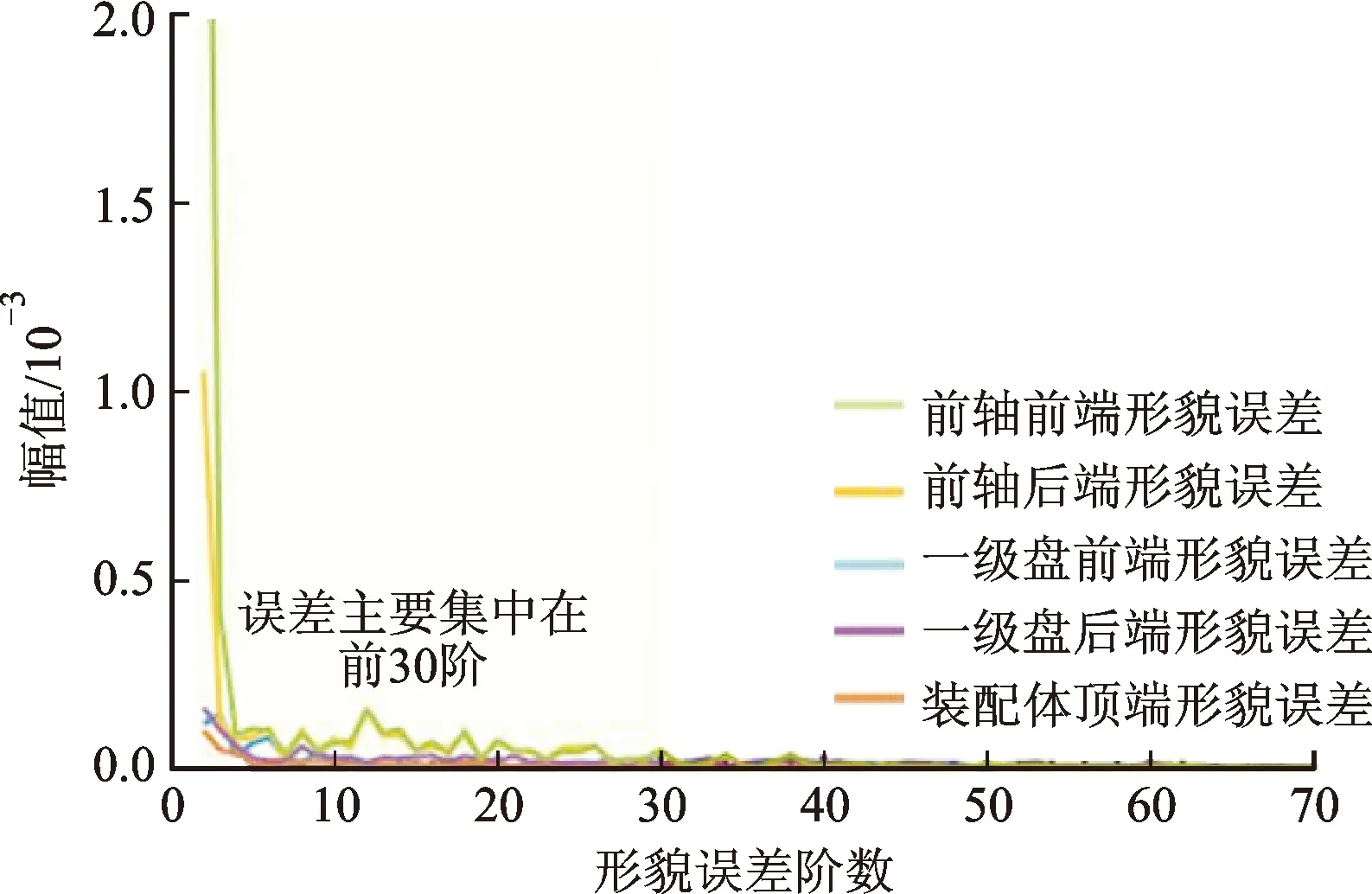
图4 端向误差数据的FFT图

图5 径向误差数据的FFT图

1.2 生成误差数据

由傅里叶变换可知,一阶傅里叶级数的幅值在[-0.001,-0.002 2]和[0.001,0.002 2]之间,其余阶数的幅值在[-0.000 2,0.000 2]之间。所有阶数的相位均在[0,2π]之间,通过Python中random模块,随机在这些区间生成相应的幅值相位,最终由式(1)和式(2)分别生成200组径向跳动误差数据和端向跳动误差数据。将径向跳动误差数据和端向跳动误差数据分别通过施加多个接触对的方式添加到有限元软件建立的模型中,即将径向和端向接触对中接触面偏移赋值为实测微小误差数据。有限元模型底面固定,使用集中力模拟螺栓预紧力,在力的作用下对有限元模型进行计算,将顶面计算结果运用最小二乘拟合得到偏心,以此作为神经网络的输出。计算结果如图6所示,本文只给出转子其中两个零件装配有限元计算结果,其他装配零件同理。

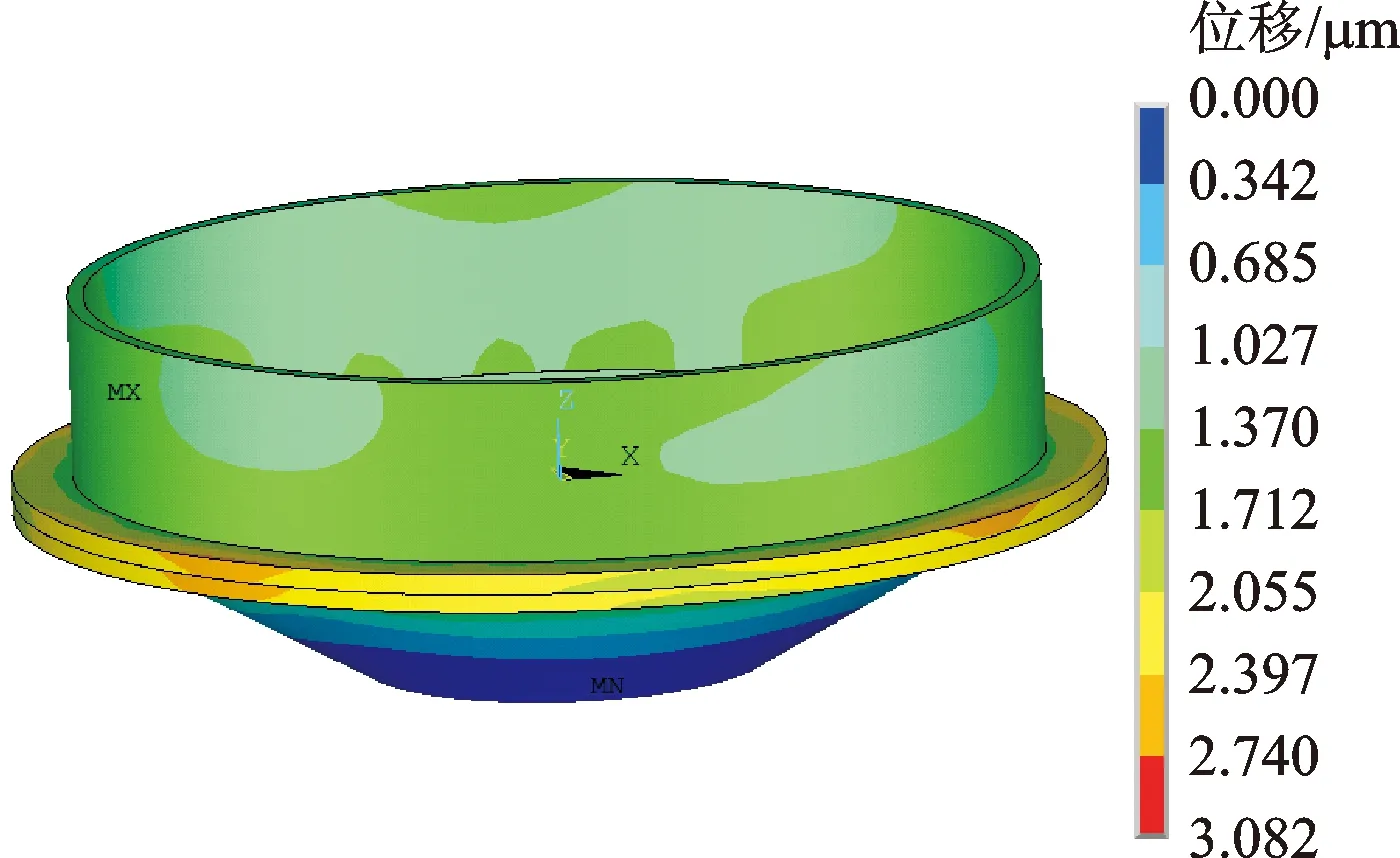
图6 有限元计算结果

2 神经网络模型预测装配偏心

由于不同航空发动机转子配合面的形貌特征不同,故装配以后对应的装配偏心也不同,两者之间必然存在复杂的非线性映射关系,因此本文通过神经网络模型来计算航空发动机转子装配偏心。

2.1 BP神经网络模型

BP神经网络能够处理多维结构数据,采用非线性连续函数作为神经元节点的激活函数,可以使整个边界线变成连续光滑的曲线,且对输入和输出具有优秀的非线性映射能力。通过BP神经网络,可以拟合航空发动机转子零件止口处轮廓的形貌误差和转子零件装配偏心之间的非线性关系。

本文搭建了两个BP神经网络,分别进行航空发动机转子零件装配偏心量(r)和偏心角(θ)预测。网络具有3层结构,由输入层、隐含层和输出层组成,如图7所示。输入层对应航空发动机转子零件止口配合面轮廓形貌误差的特征向量,即由前30阶傅里叶级数的各个阶数的幅值和相位构成,输出层对应航空发动机转子零件止口顶端的装配偏心量和偏心角。

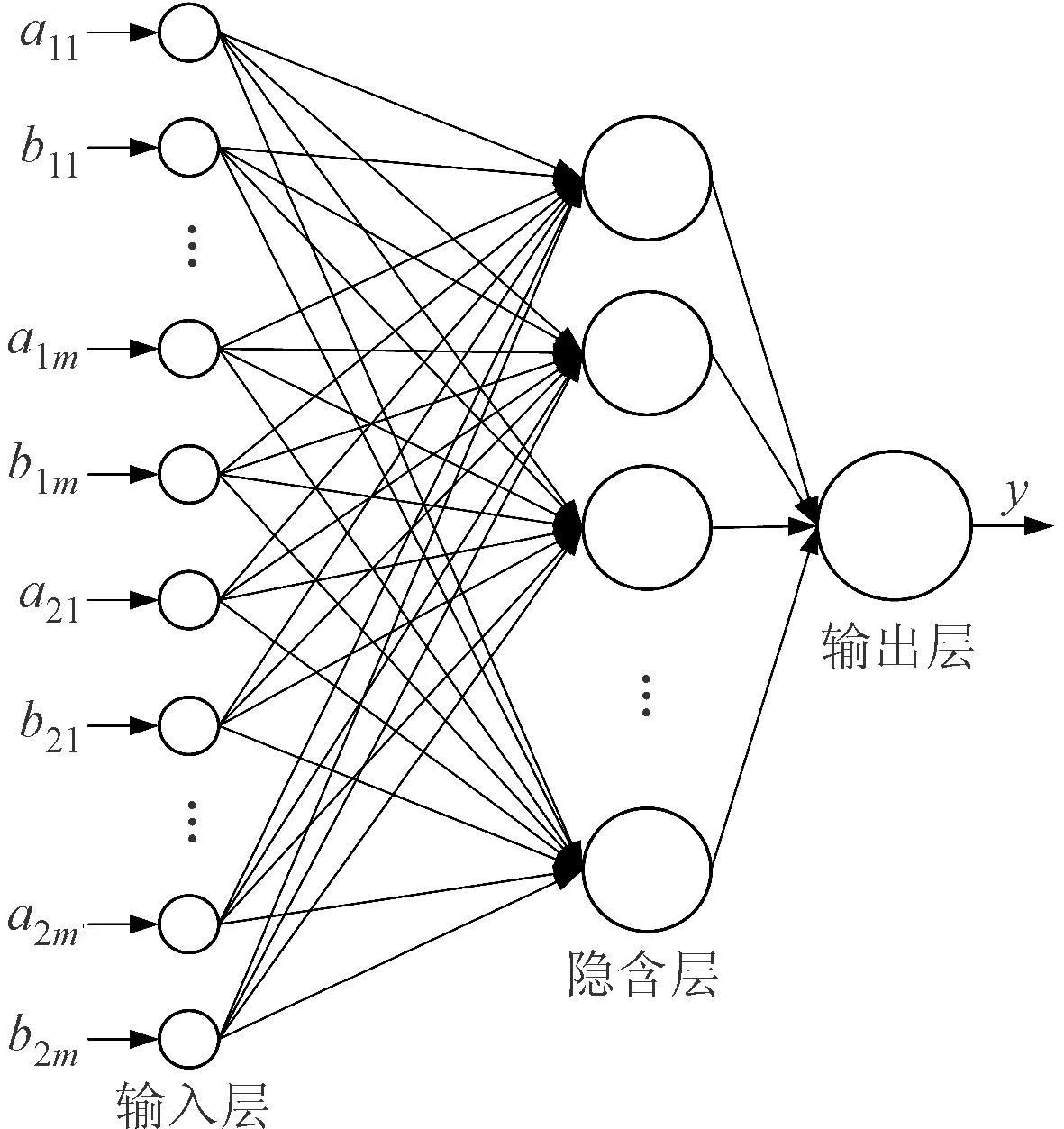
图7 BP神经网络结构

不同零件装配时,输入、输出分别都是特征向量和装配偏心,只是特征向量和装配偏心的具体数值不一样,故不同的两个装配零件只影响神经网络的具体参数。因此,本文以前轴和一级盘零件装配为例,详细说明神经网络预测的准确性,其他零件的神经网络训练也使用200组训练数据,这里不再赘述。

模型采用梯度下降优化算法,公式为

(3)

神经网络隐含层使用sigmoid函数作为激活函数,表达式为

(4)

采用均方误差为损失函数[17],表达式为

(5)

式中:y分别代表两个神经网络理论计算出的装配偏心量和偏心角;y′分别代表两个网络实际计算出的装配偏心量和偏心角。两个神经网络的输出都只有一个值,故i=1。

本文的隐含层节点数为2,为了提高训练集收敛效率使用衰减学习率,即最初学习率为0.01,学习率衰减率为0.999。最大训练次数分别为200 000和50 000,每次喂入神经网络的个数均为50个。为了防止出现过拟合,网络中加入了L2[18]正则化方法,计算公式如下

(6)

此外还使用滑动平均算法,使航空发动机转子装配偏心计算结果精准度更稳定。

2.2 神经网络训练集

本文通过傅里叶级数,生成200组转子形貌误差数据作为神经网络的输入,采用有限元方法对这200组数据做上标签(即有限元模型计算出偏心量和偏心角结果),作为网络的输出,从而进行神经网络训练,训练流程如图8所示。

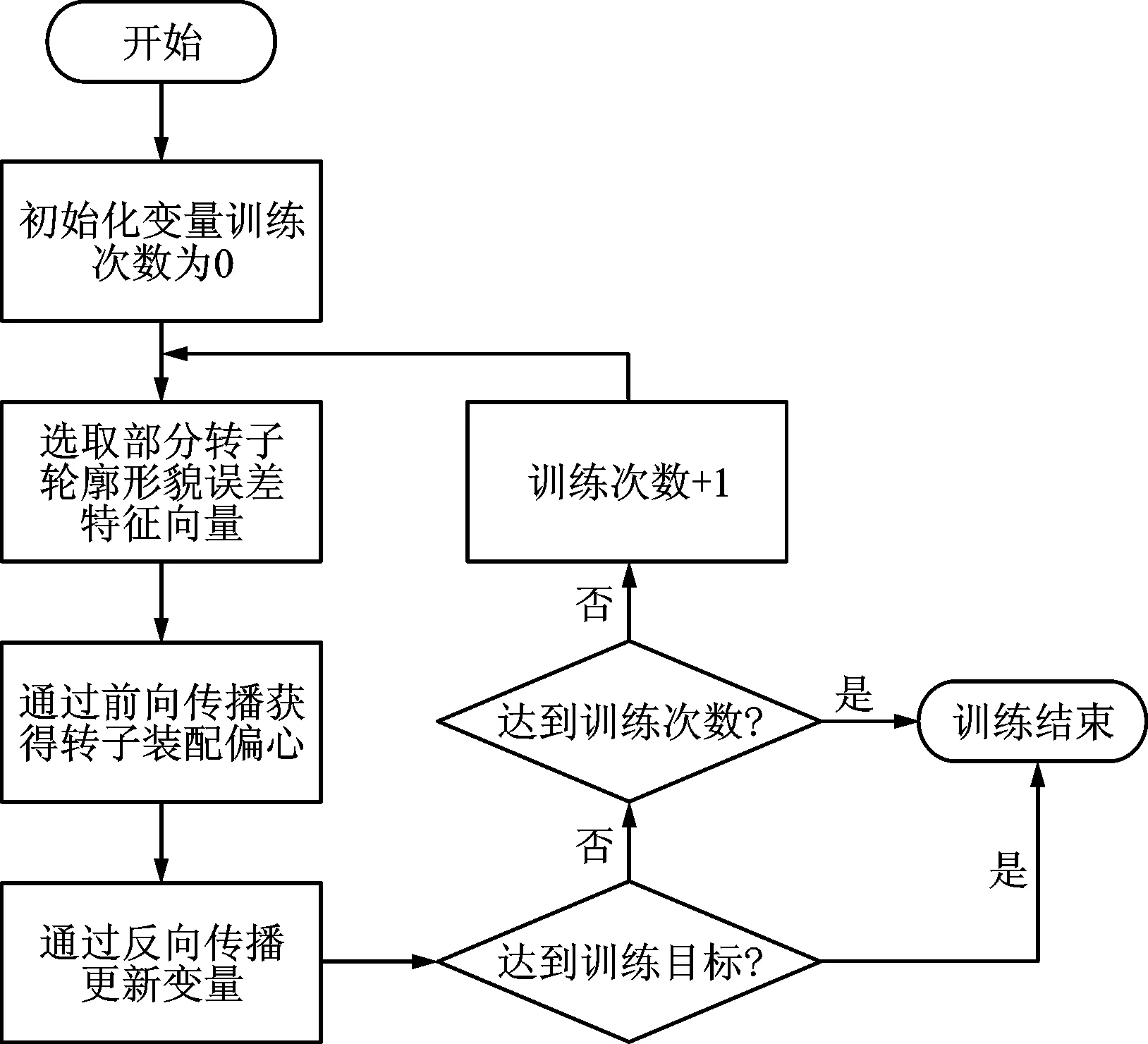
图8 神经网络训练流程图

以傅里叶级数各阶幅值、相位的参数(即表示航空发动机转子零件配合面形貌误差)作为神经网络输入的特征向量P(a11,b11,…,a1m,b1m)T,转子装配偏心为网络输出,最终分别在迭代200 000和50 000次之后,损失函数误差分别约为1.274 41×10-6mm和0.23°。训练时间分别为约5 min和2 min。

2.3 神经网络偏心预测结果

在航空发动机装配偏心预测神经网络模型参数训练完成之后,通过对新生成的3组模拟转子轮廓形貌误差进行偏心预测,以验证方法的有效性。神经网络模型对有限元方法生成的数据进行网络训练,故测试结果也应该和有限元仿真进行对比,结果如表1和表2所示。测试集计算时间约为10 s。

表1 神经网络预测装配偏心量

表2 神经网络预测装配偏心角

3 基于粒子群算法的相位优化过程

针对航空发动机转子零件装配相位可调的情况,分析不同装配相位对产品装配误差的影响,实现零部件装配相位的优化。

3.1 组合转子误差传递模型

以航空发动机转子每个零件的截面中心为原点,法向量为z轴,建立坐标系,如图9所示。该坐标系在测量坐标系中的齐次坐标矩阵描述即可表示转子零件测量面在测量坐标系中的方位[19-20]。

图9 建立的零件坐标系

此时航空发动机转子零件的齐次坐标矩阵表达式为

(7)

式中:xc和yc分别为转子零件截面中心的x、y坐标;h为截面高度;α和β分别为绕x、y轴的转角值。

通过对航空发动机转子的每个零件建立位姿矩阵,即分别表示测量坐标系中转子零件上若干特征面的空间位姿——零件各特征之间的关系,如图10所示,表示一个转子零件通过位姿变换得到止口顶端相对于底端的偏心。

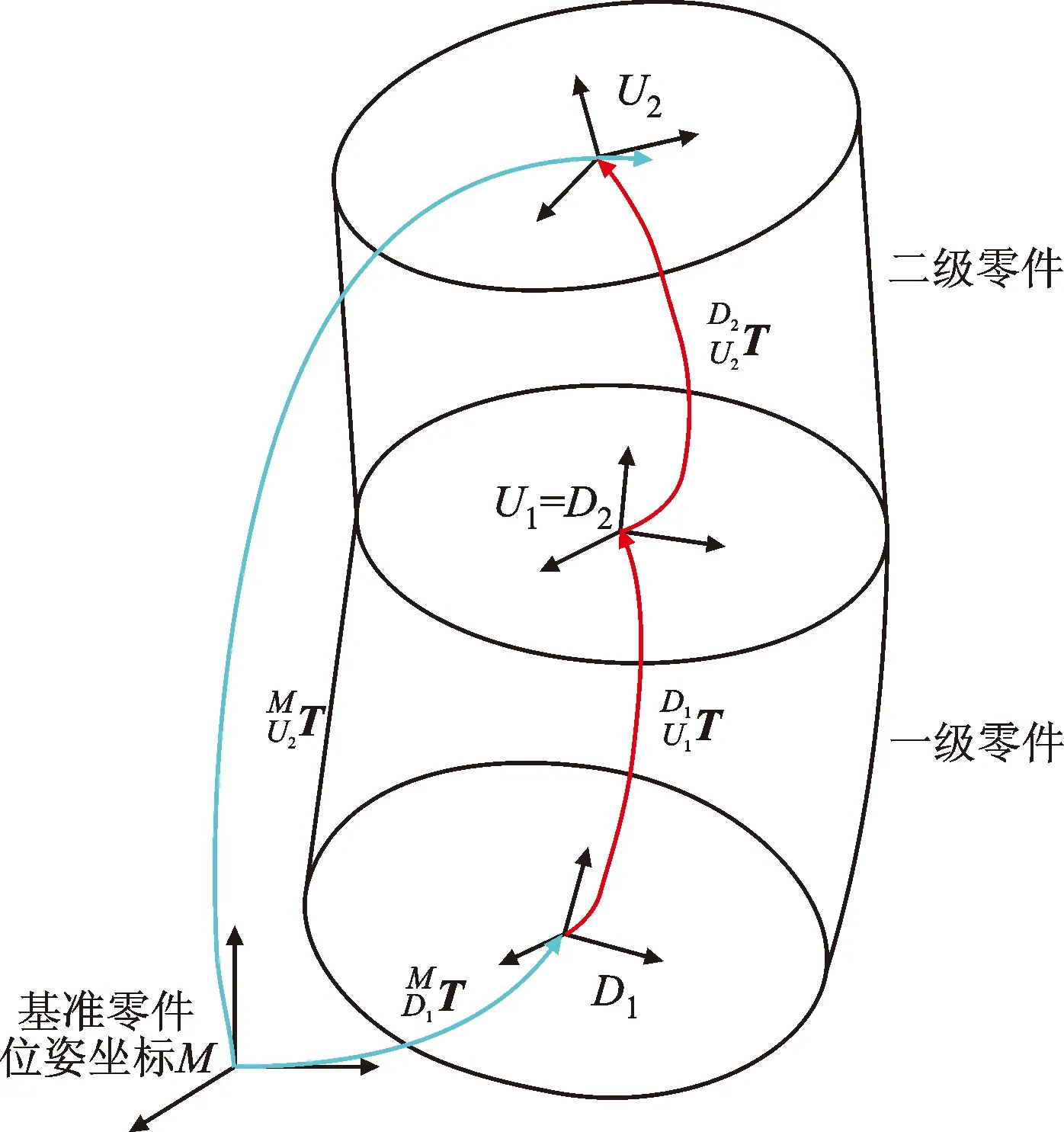
图10 误差传递模型图

当一个零件堆叠时,通过齐次坐标变换理论可知

(8)

当两个零件堆叠时,一级零件顶面圆心和二级零件底面圆心重合,二级零件顶面相对于前轴基准下的位姿为

(9)

多个零件装配时,有

(10)

最终可以提取每一级零件的偏心量r。

3.2 组合转子相位优化

大型转子常会设计为多级零件组合的形式,各级零件通过止口连接起来,最终形成一个完整的转子。航空发动机高压转子是典型的组合转子,为了获得优良的服役性能,装配精度和初始不平衡量要求极为严苛。

在组合转子装配过程中,螺栓孔通常是周向均布的,零件会有多个可选的装配相位。为了使转子整体的同心度达到最优,需要为每个零件在若干个不同装配相位中进行优选,将各级盘零件依次装配在一起,最终形成符合精度要求的组合转子。转子装配精度要求是整体的同心度,并非只关注前后两端的同轴度,并且所有零件偏心量之和应小于0.180 mm和每一级单个偏心小于0.060 mm,因此需要对每级零件的同心度都要进行分析研究。这个问题需要使用前面的装配偏心预测模型求解,得到所有零件止口的中心坐标值,进而计算整体的同心度,评价整体的装配质量。为了对各零件的偏心量进行评估,需要先确定一条基准轴线,为此止口几何中心到轴线的距离就是该面的偏心量。本文选择以最小二乘法拟合各中心点得到的公共轴线为基准,评估各零件的偏心量,可以保证装配质量,具体如图11所示。

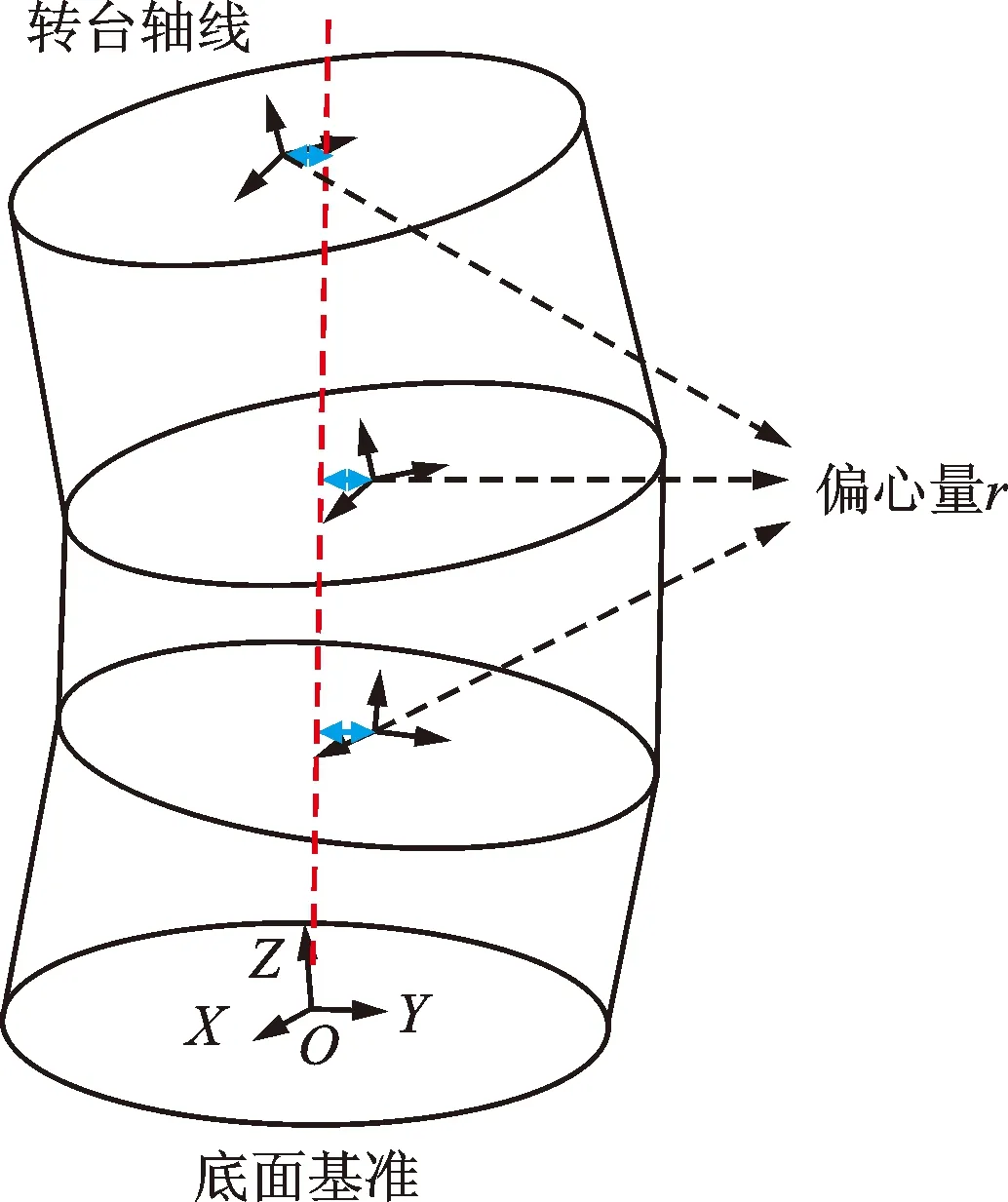
图11 零件装配偏心示意图

在每级盘偏心量都小于公差值的基础上,以各级零件偏心量之和最小作为适应度函数,进行各级盘装配角度的优化。对该优化问题建模如下

(11)

式中:n为零件数量;Tr为转子装配偏心量公差,为同心度公差的一半;r为零件偏心量。

如图12所示,模拟航空发动机转子共由6个零件组成,分别为前轴、压气机一级盘、压气机二级盘、压气机三级盘、涡轮盘和后轴。

图12 高压转子模拟件结构

为减轻重量,零件均为中空的薄壁结构,同时为了增加零件强度,一些零件中存在加强肋板,为了减少其他因素的影响,各零件上未设置叶片插槽等细节结构。各个零件的关键尺寸以及可调整相位个数如表3所示。6个零件对应的各公差值均一致,如表4所示。

表3 模拟转子各零件关键尺寸及可调整相位个数

表4 模拟转子各零件主要公差

3.3 粒子群算法求解

不同航空发动机转子零件装配时的装配角度可以调整,而且对一个零件来说,不同的相位之间不能共存,只能选择其中之一。当可选装配相位的数目很多时,使用遍历算法计算时间会非常长、效率极低。这种情况下,智能算法就成为转子装配相位选择优化问题的首选,旨在提高计算效率,得到近似全局最优的解。

粒子群算法有着实现方便、收敛速度快、参数设置少的特点,很适合进行航空发动机转子装配相位优化选择。因此,本文选用粒子群算法进行相位优化,旨在得到一组最优的装配相位组合。粒子群算法流程如图13所示,其中vid、kid为优化粒子群速度、位置,c1、c2为学习因子,r1、r2为[0,1]内的随机数。

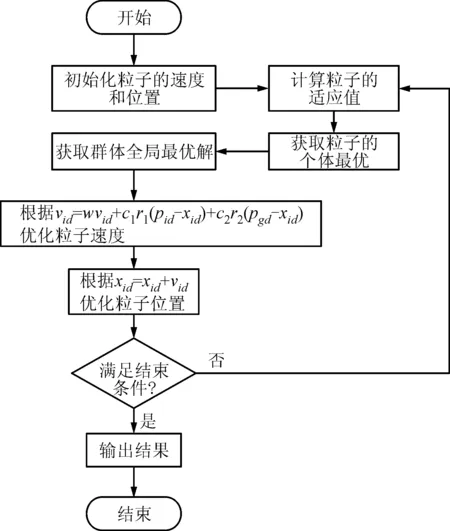
图13 粒子群算法流程图

由前30阶傅里叶级数生成转子配合面轮廓形貌误差,通过神经网络偏心预测模型,分别得到航空发动机转子不同相位下的装配偏心,再应用粒子群算法对装配相位进行优化,得到优化后的装配相位。

由于航空发动机转子装配相位的固定性,而粒子群算法进行优化时方向可能是任意的,即优化后可能不是所应装配相位位置,故选择与所应装配相位最近的位置(两个偏心点的欧氏距离最近)为最优装配相位。粒子群算法参数设置:学习因子1c1=1.5,学习因子2c2=2.5,惯性权重w=0.5,初始化群体个体数目N=50,最大迭代次数M=1,搜索空间维度(即未知数个数)D=5。

采用MATLAB软件进行粒子群算法求解,最终优化结果为前轴和压气机一级盘第28个螺孔、压气机一级盘和压二级盘第18个螺孔、压气机二级盘和三级盘第24个螺孔、压气机三级盘和高压涡轮盘第1个螺孔和后轴第6个螺孔对齐,如此装配完成后转子总偏心量为0.165 73 mm,具体优化结果比较如表5所示。

表5 粒子群算法相位优化结果

4 结 论

本文建立了人工神经网络偏心预测模型,用于计算转子不同零件装配的偏心量,针对两个相同零件有不同相位组合的情况,设计粒子群算法,从这个过程可得出如下结论。

(1)转子零件止口处的加工形貌误差主要集中在前30阶傅里叶级数和的形式,且一阶傅里叶级数的幅值在[-0.001,-0.002 2]和[0.001,0.002 2]之间,其余阶数的幅值在[-0.000 2,0.000 2]之间,所有阶数的相位均在[0,2π]之间。

(2)通过搭建人工神经网络偏心预测模型,可以快速精确地计算转子零件的装配偏心。当零件加工精度不高时,神经网络模型预测精度相对于刚体模型提高了约20%,并且计算速度从有限元模型计算两级盘约50 min提升到神经网络模型的约5 s。

(3)使用粒子群算法可以高效地完成不同相位的优化选择,从结果也可明显看出,优化以后比未优化时同心度明显要更优,最终使转子装配同心度之和小于0.180 mm的公差设计要求。