基于EBF神经网络铁路箱梁桥结构的优化
董连成,李珠君,董 军
(1.黑龙江科技大学 建筑工程学院, 哈尔滨 150022; 2.北京建筑大学 工程结构与新材料北京市高等学校工程研究中心, 北京 100044)
0 引 言
车—轨—桥耦合振动体系研究一直以来都是国内外学者研究的重点,并取得了相当的成果[1-4]。桥梁不仅承受来自上部轨道结构的长期载荷,还承受列车通过时短期冲击的载荷作用。延长桥梁寿命,提高桥梁承载能力,使其经济效益极大化,是桥梁研究的目的。以获得桥梁使用最佳状态为目标,大量学者进行了桥梁的优化研究。谢冠宇等[5]选取深圳东宝河新安大桥—三跨波形钢腹板PC组合连续箱梁桥为研究对象,研究了基于椭圆基函数(Elliptic basis function,EBF)神经网络的桥梁有限元模型修正,结果表明,椭圆基函数神经网络近似模型的模型修正较三阶响应面和径向基函数神经网络有更高的精度。殷允垚[6]将扣减刚度、过渡段长度及填料作为设计变量,对车—轨耦合作用下路桥过渡段进行优化研究。傅强等[7]研究了大跨度斜拉桥的动力优化设计。杨书仪等[8]依托响应面法和有限元技术,建立了桥梁主桁架的挠度、弯曲应力和结构尺寸的函数表达式,对11 m简支钢桥主桁架结构进行优化设计。
优化常用的近似模型有响应面模型、正交多项式模型和神经网络模型等。神经网络以其良好的拟合能力、对非线性映射关系的良好表达能力成为优化构建近似模型的常见选择,而基于EBF神经网络的算法计算效率和精度更高[5]。目前,24 m跨径箱梁桥在制作、维修、施工等方面较易实现,既有铁路和在建铁路上均有应用,如津秦铁路客运专线等。有鉴于此,笔者以铁路上常用的24 m铁路箱梁桥为例,采用时速为36 km/h的列车和德国高干扰轨道不平顺谱,分别考虑有限元模型中7个参数,先进行显著性分析,确定3个对桥梁振动影响显著的因子,针对显著因子进行了基于EBF神经网络的多目标优化研究,构建了有效的铁路箱梁桥优化设计方法,为后续铁路箱梁桥设计与仿真分析提供理论参考,并为提高铁路实际建设提供服务。
1 构建列车—轨道—箱梁桥耦合模型
1.1 模型构建及参数选取
铁路箱梁桥结构如图1a所示。模型包括轨道、轨道板、CA砂浆层、底座板、滑动层和箱梁桥。列车经过铁路箱梁桥时,钢轨传力于轨道板,之后力传递于底座板,底座板传力于桥梁。笔者以单跨24 m双线标准简支箱梁桥为研究对象,上面铺设CRTSⅡ型板式轨道板,钢轨采用标准60轨,列车采用CRH380AL列车。模型具体参数为:桥面宽12.00 m,梁高3.05 m,单跨桥梁长25.95 m,桥梁上铺设4块轨道板,底座板宽2.95 m,厚度0.20 m;CA砂浆层宽2.50 m,厚度0.03 m;轨道板宽2.50 m,厚度0.20 m;每块标准轨道板长6.45 m,板间距0.05 m。标准轨道板与钢轨设10组扣件,每两组扣件间距0.65 m。钢轨与桥梁同长度。CRH380AL列车,选取一节中间车做模拟,长度25.00 m,宽3.38 m,高3.70 m,轴重15 t,车体重40 t。有限元模型如图1b所示,扣件采用combin14线性弹簧单元,滑动层采用combin39非线性弹簧单元。

图1 铁路箱梁桥横断面与有限元模型Fig. 1 Cross section and finite element model of rail box bridge
1.2 加载条件
为获得24 m单跨简支箱梁桥振动响应,采用的加载条件如下:车辆速度为36 km/h,过桥时间为4.74 s,施加德国高干扰轨道高低不平顺谱。
其中,德国轨道高低不平顺表达式[3]:
(1)
式中:Sv——高低不平顺功率谱密度,m2/rad·m-1;
Ωc——截断频率,rad/m,取0.8246;
Av——粗糙度常数,m2·rad/m,取1.08×10-6;
Ω——轨道不平顺的空间频率,rad/m;
Ωr——截断频率,rad/m,取0.020 6。
根据逆傅里叶变换法(IFFT),利用Matlab软件对式(1)进行数值分析,得德国高干扰垂向不平顺时域样本,见图2。

图2 垂向不平顺时域样本Fig. 2 Time domain samples of vertical track irregularity
1.3 优化目标
列车经过时桥梁发生振动,该振动属于多自由度系统受迫振动,振动方程[9-10]为

(2)
式中:M——质量矩阵;
c——阻尼矩阵;
K——刚度矩阵;


Y——位移列向量;
F(t)——外荷载。
求解该方程需引入正则坐标和主振型矩阵,先求得自振频率和振型,再求广义质量和广义荷载,计算阻尼比,之后求得正则坐标,最后求得结构的位移等动力反应。故作者以降低桥梁振动、优化铁路箱梁桥结构为目的,选取可以表征桥梁振动特性跨中的挠度、加速度和1阶竖向弯曲的自振频率3个参数为优化目标(多目标优化)。
2 轨道箱梁桥结构优化设计
2.1 正交实验设计及显著因子筛选
考虑模型的复杂性,为了防止在优化仿真中因子数过多或者所选因子不显著而造成实验结果失败,暂选7组参数采用正交实验法进行参数敏感性分析,如式(3),因素水平表如表1所示。
x=(x1,x2,x3,x4,x5,x6,x7),
(3)
式中:x1——combin14弹簧刚度;
x2——combin14弹簧高度;
x3——combin39高度;
x4——combin14弹簧间距(扣件间距);
x5——轨道板混凝土强度的弹性模量;
x6——底座板混凝土强度的弹性模量;
x7——桥梁混凝土强度的弹性模量。

表1 因素水平
全因子实验所需的实验次数是和因子数呈指数相关:
r=km,
(4)
式中:r——实验次数;
k——因子水平;
m——因子数。
文中的7因子2水平的全因子实验次数为27,128次,取16次实验数据,实验设计表如表2所示,其中,a为加速度,f为自振频率。
根据对正交实验结果得出的标准化效应Pareto图可知,显著因子是对目标函数影响比较大的因子。Pareto图是可以确定影响较大参数的条形图,条形一旦超出红线部分即为显著。该图取决于误差项的自由度,当误差项的自由度大于等于1时,Pareto图则在t处绘制红线;当误差项的自由度等于0时,Pareto图则在边际误差处绘制红线,边际误差ε为
ε=t×εPSE,
(5)
式中:t——t分布的(1-α/2)分位数;
εPSE——伪标准误。
显著性水平关乎区间估计的可靠度,文中取显著性水平αs=0.1,即置信度为90%。桥梁跨中挠度的标准化效应Pareto图见图3,桥梁跨中振动加速度的标准化效应Pareto图见图4,桥梁跨中1阶竖向弯曲自振频率的标准化效应Pareto图见图5。
由图3~5可知,跨中挠度的显著因子为x1和x7,跨中加速度的显著因子为x4, 跨中1阶竖向弯曲自振频率的显著因子为x4和x7。因此,选取x1、x4和x7为设计变量,其他变量为非显著因子,取值如表3所示。根据文献[11]可知,混凝土材料动弹性模量高出静弹性模量30%~50%,针对桥梁强度选择的C50、C50的动弹性模量最大取值范围为3.45×1.5=5.18 GPa。

表2 实验设计

图3 跨中挠度Pareto图Fig. 3 Deflection Pareto diagram in mid span

图4 跨中加速度Pareto图Fig. 4 Acceleration Pareto diagram in mid span

图5 跨中1阶竖向弯曲自振频率Pareto图Fig. 5 First-order natural frequency Pareto diagram in mid span
2.2 最优拉丁超立方实验设计方法采样
由于车轨桥模型本身计算工作量大,抽样点多,因此,采用最优拉丁超立方实验设计方法获取样本点,取值如表3所示,方案如表4所示。最优拉丁超立方实验抽样方法是对拉丁超立方实验抽样方法的改进,样本点数更少,精确度更高。

表3实验设计参数
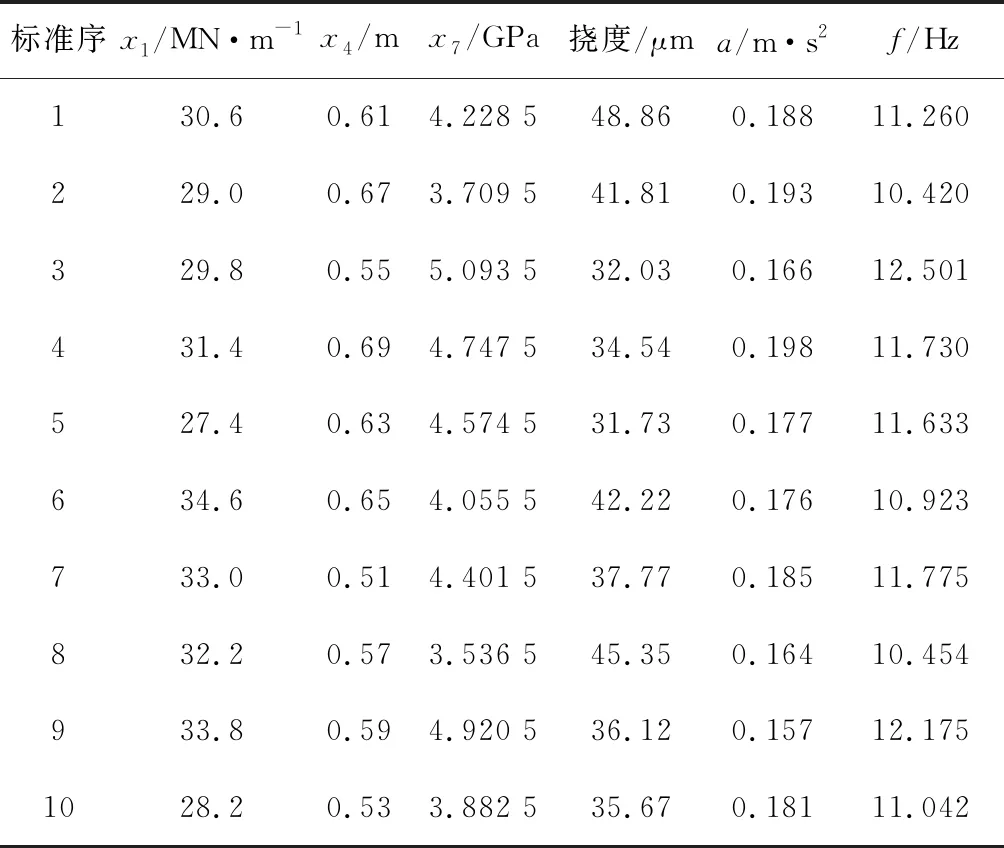
表4 最优拉丁超立方实验设计方案
2.3 EBF神经网络结构模型的构建
为了更好的优化铁路箱梁桥结构,引入椭圆基函数(Elliptic basis function,EBF)神经网络作为优化过程中的近似模型。神经网络具有可以充分逼近任意复杂的非线性关系,可并行处理方法等优点,在许多实际应用领域都取得了显著成效[12],且EBF神经网络较响应面和径向基函数神经网络具有更好的适用性和更高的精度[5]。EBF神经网络基本结构如图6所示。其中输入层的x1、x2和x3代表由正交实验确定的3个显著因子,即扣件弹簧刚度,扣件间距,桥梁混凝土强度的弹性模量,输出层的y1、y2和y3代表3个优化目标,即跨中的挠度、加速度和1阶竖向弯曲的自振频率。

图6 椭圆基函数神经网络Fig. 6 Elliptic basis function neural network
设输入层有N个输入参数,隐含层有n个神经元,输出层有M个响应值,则响应值对应的公式[5,13]:
(6)
式中:wi——第i个神经元与第M个响应值的连接权重系数;
gi——椭圆基函数。
权重系数wi可通过式(7)、(8)联立求得,椭圆基函数gi可通过式(9)求得。
(7)
(8)
gi(x)=(x-xi)TS-1(x-xi),
(9)
(10)
w=H-1y,
(11)
式中:S——协方差矩阵;
μ——样本中心点;
y=(y1,y2,…,yn,0)T。
根据表2和表3的参数取值,将其作为ANSYS有限元软件初始参数计算铁路箱梁桥跨中的挠度、加速度和1阶竖向弯曲的自振频率(优化目标),提取计算结果,如表4,从而获得神经网络训练样本集。
2.4 拟合优度分析
由于神经网络无法给出输入变量和输出变量直接的函数关系,为获得最佳近似模型,引入R2复相关系数评价模型近似程度,其表达式:
(12)
式中:yi——第i个样本点的响应值;
ypi——第i个样本点的神经网络模型近似值;

跨中的挠度、加速度及1阶竖向弯曲自振频率的椭圆基函数神经网络模型的拟合优度均在0.90以上,表明拟合所得模型能够很好的反应设计变量与响应之间的函数关系,可用于下一步优化设计。
2.5 优化设计
基于优化参数为变量,以挠度、加速度和1阶竖向弯曲的自振频率为优化目标的优化数学模型表达式为
(13)


表5 设计变量的初始值和取值范围
由于多目标优化问题中各优化目标之间可能存在交互作用,无法同时达到最优,因此选用NSGA-II遗传算法寻优,即非支配排序遗传算法,以便获取Pareto最优解集。NSGA-II遗传算法较传统的遗传算法降低了计算复杂度,保持了种群多样性,扩大了采样空间[14]。优化时,子代种群规模100,最多迭代次数100,变异概率0.03,交叉概率0.7[15]。Pareto前沿解分布图如图7所示。

图7 Pareto前沿解分布Fig. 7 Distribution of Pareto frontier solutions
根据式(13),选A点作为优化后满意解,优化后最终结果如表6所示。
结果显示,采用NSGA-II遗传算法对EBF神经网络近似模型寻优并进行调整,代入有限元模型,产生跨中的挠度、加速度和1阶自振频率误差分别为6.10%、2.84%和 6.34%,这表明该优化方法有效。由表6结果得到,与初始值相比,跨中的挠度、加速度和第1阶自振频率分别下降了7.0%、9.0%和 9.5%。

表6 优化前后设计变量和目标函数的对比
桥梁跨中的挠度,振动加速度和1阶自振频率的降低,说明桥梁振动得到了有效改善。优化后桥梁1阶模态振型如图8所示。

图8 1阶模态振型Fig. 8 Shape of first-order modal
3 结 论
针对列车通过铁路箱梁桥造成的振动,为降低对桥梁的振动,以24 m铁路箱梁桥为例,建立了铁路列车—轨道—箱梁桥有限元模型,通过正交实验从有限元模型中选取的7个参数中确定3个明显影响桥梁振动的参数(显著因子),基于EBF神经网络得出箱梁桥近似模型,通过NSGA-II遗传算法对近似模型进行优化。
(1)依据正交实验,在置信水平为90%的基础上,确定combin14弹簧刚度,扣件间距和桥梁混凝土强度的弹性模量3个显著因子,即明显影响桥梁跨中的挠度、加速度和1阶弯曲的自振频率的参数。
(2)根据NSGA-II遗传算法寻优可知,当弹簧刚度为3.33×107N/m,扣件间距为0.65 m,桥梁混凝土强度的动弹性模量4.11 GPa时,桥梁跨中的挠度、加速度和1阶弯曲的自振频率(3个优化目标)最小,桥梁振动得到有效改善。
(3)基于EBF神经网络的结构优化设计,结构跨中的挠度降低7.0%,加速度降低9.0%,1阶弯曲的自振频率降低9.5%,有效提升计算效率并保证优化结果精度,对复杂工程结构,基于EBF神经网络的优化方法同样适用。

