大攻角下典型主梁断面颤振临界风速数值模拟
刘志文 陈岳飞 陈政清


摘 要:针对大攻角下主梁断面颤振稳定性问题,基于计算流体动力学软件ANSYS FLUENT用户自定义函数UDFs和动网格技术,结合Newmark - β法建立了桥梁主梁断面二维流固耦合分析方法,采用该方法在不同攻角下(0°、±3°、±5°、±8°)对薄平板和流线型箱梁断面颤振稳定性进行数值模拟研究,并将数值模拟结果与风洞试验研究结果进行了比较. 结果表明:薄平板和流线型箱梁断面的颤振临界风速数值模拟结果与风洞试验结果吻合较好,验证了本文所建立的桥梁主梁断面二维流固耦合分析方法的精度. 薄平板断面的颤振临界风速随攻角的增大显著降低;流线型箱梁断面在正攻角范围内颤振临界风速随着攻角的增大而降低,在负攻角范围内颤振临界风速随攻角绝对值的增加先增大后降低;当攻角较大时,薄平板断面和流线型主梁断面均表现出“钝体”特征,气流绕过断面前缘时发生分离,沿断面上下缘产生较大的涡,从而导致主梁断面颤振临界风速降低.
关键词:典型主梁断面;大攻角;颤振临界风速;流固耦合;数值模拟;风洞试验
中图分类号:U441.3 文献标志码:A
文章编号:1674—2974(2021)01—0082—10
Abstract:Aiming at the flutter stability of the main girder section at high attack angles, this paper studies the flutter stability of a thin plate and a streamlined box girder section at different attack angles(0°,±3°,±5°,±8°)by numerical simulation method. Two-dimensional fluid-structure interaction(FSI) method combined with Newmark-β method is developed based on ANSYS FLUENT user-defined function(UDFs) and dynamic mesh technology. Meanwhile, the numerical simulation results are compared with the wind tunnel test data. The results show that the critical flutter wind speeds of the thin plate section and the streamlined box girder section obtained from numerical simulation method are in good agreement with those from wind tunnel tests, which verifies the accuracy of the two-dimensional FSI analysis method for bridge deck section. The flutter critical wind speed of the thin plate section decreases significantly with the increase of attack angle. The flutter critical wind speed of the streamlined box girder section decreases with the increase of attack angle in the range of positive attack angles, and increases firstly and then decreases with the increasing of absolute values of attack angles in the range of negative attack angles. When the attack angle is large enough, the thin plate section and the streamlined deck section all characterize bluff body, and therefore the incoming flow passes around the leading edge of the section separates and generates large vortices along the upper and lower edges of the section, which leads to a decrease of the critical flutter wind speeds of the bridge girder section.
Key words:typical main deck sections;high attack angle;critical flutter wind speed;fluid-structure interaction;numerical simulation;wind tunnel tests
大攻角對颤振稳定性的影响最早在机翼断面颤振稳定性研究中受到关注. 当攻角增大到一定程度时,机翼断面的气动力与飞行状态参数之间呈现明显的非线性关系,线性理论模型已经不再适用. 国内外学者[1-2]对此进行了深入研究,目前大攻角对机翼颤振性能影响的研究已经较为成熟. 近年来,随着桥梁跨度的不断增大,桥梁主梁结构在风作用下的静力变形会进一步增大,导致主梁在高风速条件下附加风攻角增大;另外复杂山区地形及峡谷地形桥位风场由于受局部地形影响,主梁高度处存在较大的来流风攻角. 因此,大攻角下主梁断面的颤振稳定性问题逐渐受到关注.
关于大攻角下桥梁主梁断面抗风性能的研究主要集中在大攻角下主梁断面静气动力系数、颤振性能和涡振性能等方面的研究. 大攻角下主梁断面静气动力系数研究方面,Reinhold等[3-4]分别采用风洞试验和数值模拟方法研究了薄平板和流线型箱梁断面三分力系数随攻角的变化,结果表明攻角对气动升力系数的影响最为显著,升力系数在一定的攻角范围内会出现先增加后减小的趋势.
随着桥梁跨度的增加,高风速条件下主梁断面附加攻角逐渐增大,部分学者开展了附加风攻角对主梁断面颤振性能的影响研究. 许福友等[5]在进行苏通大桥全桥气弹模型的三维颤振分析过程中,发现接近颤振失稳临界状态时主梁断面的附加攻角达到了1.5°,若不考虑附加攻角的影响会高估该桥的颤振临界风速. 朱青等[6]通过弹性悬挂风洞试验研究了附加攻角对象山港大桥钢箱梁节段模型颤振临界风速的影响,从气动导数的角度分析了颤振临界风速降低的原因. 朱乐东等[7]研究了附加风攻角对扁平箱梁颤振的影响,近似10%的攻角增量也会引起颤振风速的显著变化. 张宏杰等[8]采用风洞试验的方法研究了附加攻角对钢箱梁斜拉桥颤振稳定性影响,结果表明,考虑附加攻角影响的颤振分析得到的结果更为合理. 欧阳克俭等[9]采用强迫振动试验装置研究了附加攻角对洞庭二桥桁架加劲主梁断面初步设计方案颤振临界风速的影响,结果表明,附加攻角效应会降低桁架加劲梁的颤振临界风速. 刘志文等[10]采用自由振动风洞试验结合数值模拟的方法研究了伶仃洋大桥箱梁断面的不同方案在0°、±3°和±5°下的颤振临界风速,结果表明各方案下的颤振临界风速在正攻角范围内均随攻角的增大而降低,而在负攻角范围内随攻角的增大而增大. 同时,风攻角的增加还会直接改变桥梁结构的颤振性能. 当风攻角增加时,主梁断面形状相对来流风变钝,颤振性能会由小攻角下的非线性较弱的发散型振动(硬颤振)转变为大攻角下的非线性自限幅极限环振动(LCO),即软颤振现象[11-15].
颤振导数是表征桥梁颤振性能的重要参数,通过强迫振动风洞试验,研究大攻角下不同断面的颤振导数,对颤振稳定性分析具有重要意义. 刘慕广等[16]采用强迫振动装置分别对矩形断面和H型断面气动导数的识别方法进行了试验研究,结果表明在大攻角下有必要采取与结构实际振动一致的模态来识别气动导数. Tang等[17-18]采用数值模拟方法分别研究了中央开槽平板断面和桁架加劲梁断面在不同攻角下的颤振性能,结果表明,中央开槽平板断面的颤振导数A*2在6°攻角下(桁架加劲主梁断面在8°攻角下)开始出现由负变正的趋势,颤振形式由弯扭耦合颤振变为扭转颤振;随着攻角的增加,斷面的气动特性接近钝体,颤振临界风速显著降低. 王骑等[19]采用强迫振动和自由振动风洞试验的方法,对薄平板在不同攻角下的颤振特性进行了研究,结果表明在7°攻角下,当折算风速Vred > 15时,薄平板的颤振导数A*2变为正值,且薄平板在7°攻角内采用Scanlan线性颤振导数计算的颤振临界风速仍是可靠的.
大攻角对桥梁涡振性能的影响也受到关注. 杨阳等[20]采用风洞试验对大攻角下的涡激振动性能进行了研究,结果表明大攻角下扁平箱梁的涡振振幅和范围明显增大,对于桥址位于山区等容易发生大攻角地区的桥梁应进行大攻角试验. 刘小兵等[21]研究了单箱梁在-5° ~ 5°攻角范围内涡激振动性能的变化情况,研究表明随着风攻角的逐渐减小,单箱梁涡激振动的风速锁定区间逐渐变短,最大振幅值逐渐变小,涡激振动性能逐渐变好.
综上可知,目前关于大攻角下桥梁主梁断面的颤振性能研究主要采用风洞试验方法进行研究,且研究的攻角范围大多数为-5° ~ 5°. 本文在已有研究文献的基础上采用数值方法进行典型主梁断面在大攻角条件下的颤振稳定性研究,并对大攻角对主梁断面颤振性能影响机理进行研究.
1 典型断面简介
分别针对宽高比B/D=22.5的薄平板(B为薄平板断面宽度,D为薄平板断面高度)和几何缩尺比为1/50的大带东桥(Great Belt East Bridge,GBEB)主梁断面进行大攻角下颤振性能研究. 主梁断面具体几何尺寸分别见图1和图2,对应的结构动力特性参数见表1.
2 数值模拟方法介绍
2.1 流体控制方程
不可压黏性流体的动量方程(即N-S方程)表示为:
式中:t为时间;ρ为空气密度,ρ = 1.225 kg/m3;ui、uj分别为速度分量;p为压力;υ为运动黏性系数.
2.2 湍流模型
大涡模拟(Large Eddy Simulation,LES)的基本假设为:1)动量、能量、质量及其他标量主要由大涡输送;2)流动的几何和边界条件决定了大涡的特性,且流动特性主要由大涡体现; 3)小尺度旋涡受几何和边界条件影响较小,并且各向同性. 大涡模拟过程中,直接求解大涡,而利用亚网格尺度模型模拟小尺度紊流运动对大尺度紊流运动的影响.
大涡模拟的控制方程通过对N-S方程进行空间滤波得到,即
另需要指出的是,由于旋涡具有空间三维特性,LES模拟需要进行三维分析来反应实际流动,但陈艾荣等[22]和詹昊等[23]采用二维LES模拟分别对方柱和大带东桥进行研究后发现,二维和三维大涡模拟数值结果均与试验结果吻合较好,三维大涡计算结果整体略好于二维大涡模拟结果,但二维大涡模拟计算效率远高于三维大涡模拟. 综上,本文采用二维LES模拟对薄平板和典型流线型箱梁断面的颤振稳定性进行直接计算分析.
2.3 流固耦合分析方法
采用LES模型求解不可压缩黏性流体N-S方程,结合动网格技术将Newmark-β算法通过UDF嵌入Fluent中,建立主梁断面二维流固耦合分析方法(Flutter solid interaction,FSI)[24].
以结构竖向振动为例来介绍具体的流固耦合分析方法,其中结构振动方程为:
式中:m为结构单位长度质量(kg/m);c为阻尼系数(N·s/m);k为刚度(N/m);F(t)为结构单位长度受到的竖向气动力,通过求解流体动力学方程获得.
采用Newmark-β法求解结构振动方程:
2.4 计算域及网格
取薄平板计算域为26B × 10B,示意图如图3所示. 对应的边界条件为:计算域左侧为速度入口边界(Velocity inlet),计算域右侧为速度出口边界(Pressure outlet),计算域上、下侧为对称边界(Symmetry),断面边界为固定壁面边界条件(Wall). 薄平板断面计算风攻角范围(0°~8°)对应的阻塞率范围为0.44%~1.65%. 流线型箱梁断面计算域为26B × 10B,边界条件设置与薄平板断面计算边界条件一致,在计算风攻角范围内(-8°~+8°)对应的阻塞率范围为1.40%~2.31%,满足阻塞率小于5%的要求. 为计算方便,通过改变速度入口边界参数,模拟来流的不同攻角.
计算域网格划分采用“刚体运动网格+动网格+静态网格”方案,其中刚体运动网格区域和静态网格区域采用结构化网格,动网格区域采用非结构网格. 薄平板与流线型箱梁断面的局部网格划分分别见图4和图5. 对应的首层网格高度均为0.000 1 m,边界层内网格增长率分别为1.2和1.018,对应的无量纲高度Y+均小于1. 相应断面网格数量分别约为50 380和99 470.
2.5 无关性验证
1)网格无关性验证. 主梁断面三分力系数定义如下:
式中:CH、CV和CM分别为体轴坐标系下主梁断面水平力系数、竖向力系数和力矩系数;FH、FV和MT分别为主梁断面水平力、竖向力和扭矩;U为来流风速(m/s);长度L取1 m. 综合考虑网格精度与计算时间,首先进行了薄平板断面和流线型箱梁断面网格无关性验证.
图6(a)给出了薄平板断面不同网格方案,即TP-Mesh-1(网格数为34 650)、TP-Mesh-2(网格数为50 380)和TP-Mesh-3(网格数为92 680)的网格无关性验证结果;图6(b)为流线型箱梁断面不同网格方案,即GBEB-Mesh-1(网格数为68 420)、GBEB-Mesh-2(网格数为99 470)和GBEB-Mesh-3(网格数为148 520)的网格无关性验证结果. 由图6可知,两种断面采用不同网格方案得到的体轴坐标系下的三分力系数十分接近,为了兼顾求解效率和计算精度,分别采用TP-Mesh-2和GBEB-Mesh-2的網格方案进行后续计算.
2)时间步无关性检验. 薄平板和流线型箱梁断面分别采用TP-Mesh-2和GBEB-Mesh-2的网格方案,在0°攻角下进行断面时间步无关性验证. 图7分别给出了两种断面在不同时间步长下流固耦合计算的扭转位移(α/(°))时程曲线和无量纲竖向位移(Y/D)时程曲线. 薄平板断面(0.000 2 s、0.000 5 s和0.001 s)和流线型箱梁断面(0.000 1 s、0.000 2 s、0.000 5 s和0.001 s)在不同时间步长下计算得到的位移时程曲线基本一致. 薄平板在不同时间步长下计算的扭转频率分别为2.48 Hz、2.59 Hz和2.56 Hz,时间步为0.000 5 s和0.001 s的结果更为接近,因此取时间步长为0.000 5 s进行计算. 流线型箱梁在不同时间步长下计算的扭转频率分别为4.09 Hz、4.08 Hz、4.03 Hz和4.09 Hz,因此取时间步长为0.000 2 s进行计算.
2.6 参数设置
采用LES中的Smagorinsky-Lilly湍流模型,Smagorinsky常数Cs = 0.10;速度-压力耦合求解采用SIMPLEC格式;空间离散梯度、压力和动量分别采用Green-Gause Node Based、Second Order和Bounded Central Differencing;时间离散采用Second Order Implicit格式.
3 节段模型颤振稳定性试验
为验证数值模拟的精度,需进行薄平板断面和流线型箱梁断面颤振临界风速的风洞试验测试. 薄平板与流线型箱梁断面节段模型断面几何尺寸分别见图1和图2,模型的长度均为L = 1.54 m. 模型骨架采用铝合金制作而成,外衣分别采用优质木板和ABS板制作,以保证几何外形和刚度的设计要求. 为了确保节段模型周边流动的二元性,在薄平板节段模型和流线型箱梁节段模型的端部设置了尺寸分别为780 mm×160 mm×2 mm和270 mm×103.5 mm×2 mm的端板(端部设圆弧倒角).
采用弹性悬挂主梁节段模型进行不同攻角条件下薄平板断面和颤振临界风速试验研究. 根据表1所示的薄平板断面和流线型断面节段模型动力特性参数,进行节段模型风洞试验参数设计. 模型振动位移响应采用激光位移计测试,采用东华DH5920多通道信号采集系统进行数据采集,采样频率为200 Hz. 分别进行了不同攻角下的薄平板断面(α = 0°,+3°,+5°,+8°)和流线型箱梁断面(α=-8°,-5°,-3°,0°,+3°,+5°,+8°)的颤振稳定性试验. 图8为薄平板断面和流线型箱梁断面节段模型风洞试验照片.
4 结果分析
4.1 0°攻角下的颤振临界风速结果分析
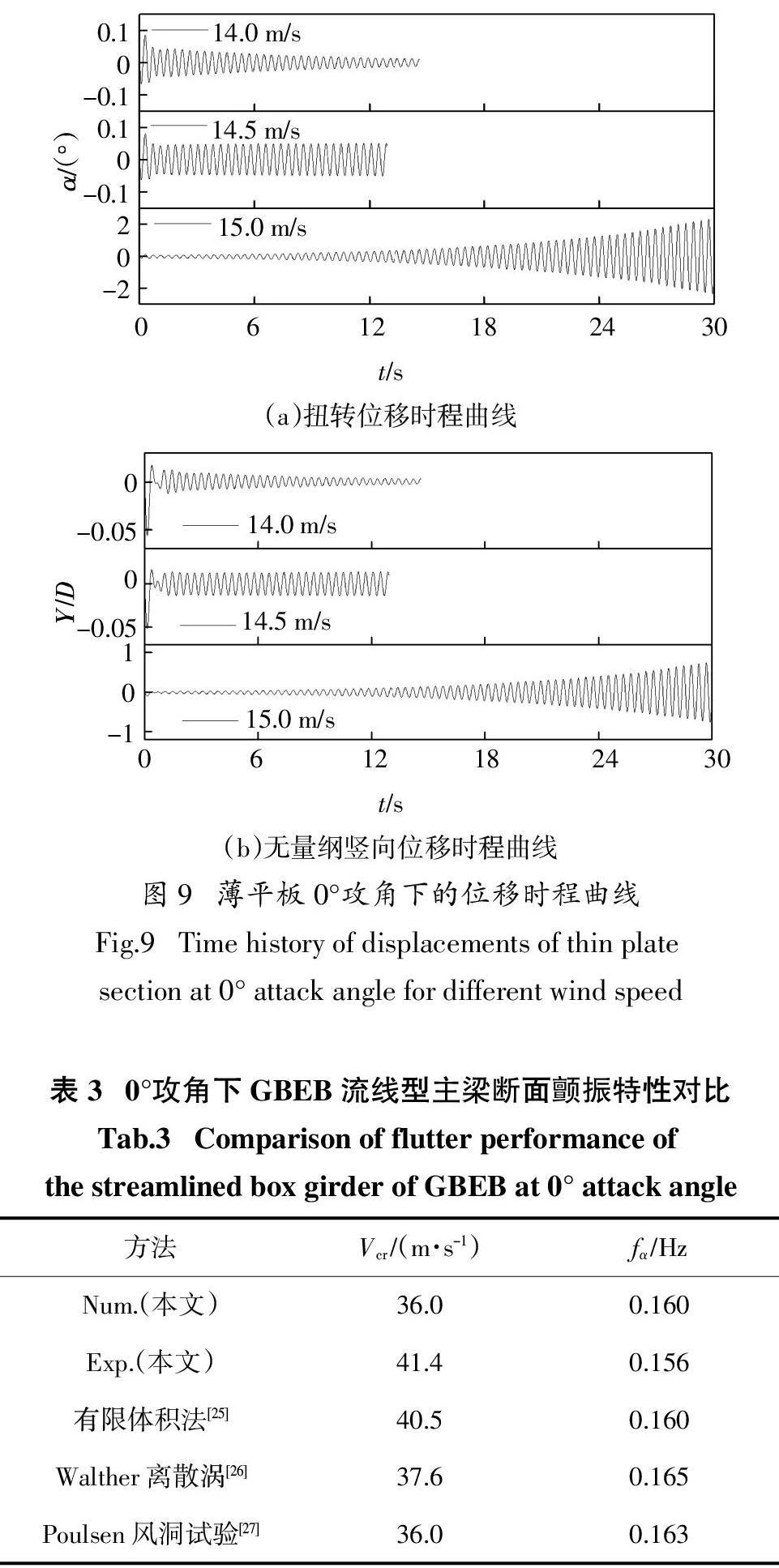
首先将0°攻角下薄平板颤振临界风速Vcr和颤振临界状态扭转频率fα的流固耦合数值模拟结果(Num.)与颤振临界风速理论解及试验结果(Exp.)进行对比,以验证数值模拟方法的精度,对比结果如表2所示. 0°攻角下薄平板断面颤振临界风速和颤振发生扭转频率的数值模拟结果与理想平板颤振临界风速和颤振扭转频率的理论计算结果较为接近,相对误差分别为-0.14%和-0.39%;且数值模拟结果与试验结果也较为吻合,验证了本文所建立的主梁流固耦合数值模拟方法的计算精度. 图9为薄平板断面0°攻角、不同风速下结构竖向和扭转振动位移响应时程曲线.
采用相同的方法得到0°攻角下GBEB桥流线型主梁断面颤振临界风速结果汇总,具体如表3所示. 0°攻角下GBEB桥流线型主梁断面数值模拟结果和风洞试验结果分别为18.0 m/s和20.7 m/s,对应的扭转频率分别为4.00 Hz和3.90 Hz,换算到实桥的风速结果分别为36.0 m/s和41.4 m/s(风速比为1 ∶ 2),对应的扭转频率分别为0.160 Hz和0.156 Hz(頻率比为1 ∶ 25). 由表3可知,GBEB桥流线型主梁断面数值模拟结果与风洞试验结果、有限体积法计算结果[25]、Walther离散涡计算值[26]和Poulsen风洞试验结果[27]之间的相对误差分别为-13.04%、-11.11%、-4.26%、0.0%.
4.2 不同攻角下颤振临界风速结果分析
分别采用流固耦合方法和风洞试验方法,对两种典型断面的弹性悬挂节段模型进行了不同攻角、不同风速下风致振动响应计算和试验研究. 表4给出了两种典型断面的数值模拟与风洞试验之间的对比结果. 由表4可知,薄平板断面颤振临界风速均随攻角的增加而逐渐降低,不同攻角下薄平板断面颤振临界风速的数值模拟结果与试验结果总体较为接近,最大相对误差为-7.8%;流线型主梁断面在正攻角范围内的颤振临界风速随攻角的增加而逐渐减小,负攻角范围内在-3°攻角时最大,-5°攻角时次之,-8°攻角时最低,接近0°攻角时的颤振临界风速,不同攻角下流线型箱梁断面颤振临界风速的数值模拟结果与试验结果最大相对误差为-18.6%,且数值模拟计算结果普遍低于风洞试验结果,这一现象及误差范围与苏通大桥的研究结果相近[15].
图10和图11分别给出了两种断面在不同攻角下扭转位移幅值根方差和竖向位移幅值根方差随风速变化的数值模拟结果,图中箭头代表该风速下的位移响应已经发散,位移会继续发展. 由图10和图11可以看出,薄平板在+5°攻角范围内的颤振特性均表现为“硬颤振”的特点,而在+8°攻角时却表现为“软颤振”的特点. 流线型箱梁断面在不同攻角下的颤振特性都表现出“软颤振”的特点,表明主梁断面“软颤振”的发生与攻角和断面形状有关.
值得指出的是,由图10和图11可知,薄平板断面通过数值模拟得到的不同攻角下的颤振性能均表现为硬颤振特性,而试验结果在+8°攻角下由硬颤振转变为软颤振. 其次,两种断面通过数值模拟方法得到的位移响应幅值和通过风洞试验得到的位移响应幅值之间具有较大的误差,即两种方法得到的后颤振性能不同,尤其是流线型箱梁断面(两种方法得到的位移响应幅值范围均可在文献中找到相似的结果[13,15]).以上现象的存在是由于在数值模拟方法中考虑了主梁断面附加攻角及气动力非线性的影响,而风洞试验方法在考虑主梁断面附加攻角和气动力非线性的基础上,还考虑了支承弹簧位置变化引起的非线性阻尼因素,使主梁断面在后颤振过程中表现出强非线性自限幅极限环振动,由此造成了主梁断面颤振后振动响应的数值模拟结果较风洞试验结果偏大.
4.3 分析与讨论
为了进一步分析攻角对主梁断面颤振临界风速的影响机理,图12和图13分别给出了薄平板断面和流线型箱梁断面在0°和+8°攻角下以颤振临界风速振动时一个周期内不同时刻(T/4、T/2、3T/4、T)的流场涡量图. 由图12和图13可知,0°攻角下,薄平板(Vcr = 14.5 m/s)和流线型箱梁断面(Vcr =18.0 m/s)仅在尾部存在明显的旋涡脱落,前沿上下表面没有明显的前沿涡,仅涡量大小发生轻微变化. 而当攻角增大至+8°时,两种断面表现出“钝体”特征,薄平板(Vcr =7.0 m/s)和流线型箱梁断面(Vcr =10.5 m/s)不仅在尾部存在严重的旋涡脱落,其前沿也出现了边界层分离,以致前沿存在明显的周期性变化的大尺度旋涡. 这种前沿涡的出现会导致桥梁结构表面压力分布不均,产生较大的扭矩,进一步激发结构的气动不稳定状态,导致结构在较低的风速下提前进入颤振.
5 结 论
本文基于计算流体动力学软件ANSYS FLUENT用户自定义函数UDF和动网格技术,结合Newmark-β法建立了桥梁主梁断面二维流固耦合分析方法,采用该方法对不同攻角下(0°、±3°、±5°、±8°)薄平板和流线型箱梁断面颤振临界风速进行数值模拟研究,并与风洞试验研究结果进行比较,得到如下主要结论:
1)薄平板断面和流线型箱梁断面颤振临界风速数值模拟结果与风洞试验结果及已有文献结果吻合较好,表明本文所建立的桥梁断面流固耦合分析方法的精度满足要求.
2)在正攻角范围内,薄平板断面和流线型箱梁断面颤振临界风速随着攻角的增加显著降低;在负攻角范围内,流线型箱梁断面的颤振临界风速随攻角绝对值的增加先增加后降低. 薄平板在+8°攻角时的颤振性能由“硬颤振”变为“软颤振”,而流线型箱梁断面在不同攻角下的颤振性能均表现为“软颤振”.
3)当攻角较大时,薄平板断面和流线型箱梁断面均表现出“钝体”特征,来流空气绕过断面前缘时发生分离,形成周期性变化的大尺度旋涡,造成主梁结构表面压力分布不均,产生较大的扭矩,进一步激发结构的气动不稳定状态,从而导致主梁断面颤振临界风速降低.
参考文献
[1] YAYLA S,CANPOLAT C,SAHIN B,et al. The effect of angle of attack on the flow structure over the nonslender lambda wing[J].Aerospace Science and Technology,2013,28(1):417—430.
[2] 汪清,蔡金狮. 飞机大攻角气动力建模研究进展[J]. 气动实验与测量控制,1994,8(3):7—17.
WANG Q,CAI J S. Advances in aerodynamic modeling of airplane at high angles of attack[J]. Aerodynamic Experiment and Measurement Control,1994,8(3):7—17. (In Chinese)
[3] REINHOLD T A,BRINCH M,DAMSGAARD A. Wind tunnel tests for the Great Belt Link[C]// Proceedings of the First International Symposium on Aerodynamics of Large Bridges. Rotterdam:Balkema Publishers,1992,2:255—267.
[4] LAROSE G L,LIVESEY F M. Performance of streamlined bridge decks in relation to the aerodynamics of a flat plate[J]. Journal of Wind Engineering and Industrial Aerodynamics,1997,69/70/71:851—860.
[5] 許福友,陈艾荣. 苏通大桥三维颤振分析[J]. 工程力学,2008,25(8):139—144.
XU F Y,CHEN A R. 3-D flutter analysis of Sutong Bridge[J]. Engineering Mechanics,2008,25(8):139—144. (In Chinese)
[6] 朱青,朱乐东,郭震山. 节段模型静风附加攻角对颤振性能的影响[C]//第十四届全国结构风工程学术会议论文集. 北京:中国土木工程学会,2010:719—724.
ZHU Q,ZHU L D,GUO Z S. Effect of additional angle of attack on flutter performance of segmental mode[C]// Papers Collection of the Fourth National Academic Conference on Structural Wind Engineering. Beijing:China Civil Engineering Society,2010:719—724. (In Chinese)
[7] 朱乐东,朱青,郭震山. 风致静力扭角对桥梁颤振性能影响的节段模型试验研究[J]. 振动与冲击,2011,30(5):23—26.
ZHU L D,ZHU Q,GUO Z S. Effect of wind-induced static torsional angle on flutter performance of bridges via sectional model test[J]. Journal of Vibration and Shock,2011,30(5):23—26. (In Chinese)
[8] 张宏杰,朱乐东. 附加风攻角对1400 m斜拉桥颤振分析结果的影响[J]. 振动与冲击,2013,32(17):95—99.
ZHANG H J,ZHU L D. Influence of additional attack angle on flutter performance of a 1 400 m long cable stayed bridge [J]. Journal of Vibration and Shock,2013,32(17):95—99. (In Chinese)
[9] 欧阳克俭,陈政清. 中央稳定板提高颤振稳定性能的细观作用机理[J]. 振动与冲击,2016,35(1):11—16.
OUYANG K J,CHEN Z Q. Micro-mechanism of a central stabilizer for improving a bridges flutter stability[J]. Journal of Vibration and Shock,2016,35(1):11—16. (In Chinese)
[10] 刘志文,谢普仁,陈政清,等. 大跨度流线型箱梁悬索桥颤振稳定性气动优化[J]. 湖南大学学报(自然科学版),2019,46(3):1—9.
LIU Z W,XIE P R,CHEN Z Q,et al. Aerodynamic optimization of flutter stability for a long-span streamlined box girder suspension bridge[J]. Journal of Hunan University(Natural Sciences),2019,46(3):1—9. (In Chinese)
[11] DAITO Y,MATSUMOTO M,ARAKI K. Torsional flutter mechanism of two-edge girders for long-span cable-stayed bridge[J]. Journal of Wind Engineering and Industrial Aerodynamics,2002,90(12/13/14/15):2127—2141.
[12] 朱乐东,高广中. 典型桥梁断面软颤振现象及影响因素[J]. 同济大学学报(自然科学版),2015,43(9):1289—1294.
ZHU L D,GAO G Z. Influential factors of soft flutter phenomenon for typical bridge deck sections[J]. Journal of Tongji University(Natural Science),2015,43(9):1289—1294. (In Chinese)
[13] 朱青,陈文天,朱乐东,等. 大攻角下超大跨度斜拉桥颤振性能节段模型风洞试验[J]. 中国公路学报,2019,32(10):67—74.
ZHU Q,CHEN W T,ZHU L D,et al. Flutter performance of a super-long-span cable-stayed bridge under large attack angles via wind tunnel sectional model tests[J]. China Journal of Highway and Transport,2019,32(10):67—74. (In Chinese)
[14] 吴长青,张志田,张伟峰. 考虑几何非线性的桥梁后顫振极限环特性[J]. 湖南大学学报(自然科学版),2018,45(5):1—10.
WU C Q,ZHANG Z T,ZHANG W F. Limit cycle oscillation of bridge post-flutter with geometric nonlinearities[J]. Journal of Hunan University(Natural Sciences),2018,45(5):1—10. (In Chinese)
[15] 窦然.大跨桥梁颤振与流动控制数值模拟[D].哈尔滨:哈尔滨工业大学,2015:45—55.
DOU R. Numerical simulation of flutter and flow control for long-span bridges[D]. Harbin:Harbin Institute of Technology,2015:45—55. (In Chinese)
[16] 刘慕广,陈政清. 典型钝体断面大攻角下的颤振自激力特性[J]. 振动与冲击,2013,32(10):22—25.
LIU M G,CHEN Z Q. Characteristics of self-excited forces in flutter of typical blunt body under large attack angles[J]. Journal of Vibration and Shock,2013,32(10):22—25. (In Chinese)
[17] TANG H J,LI Y L. Flutter performance of central-soltted plate under large wind attack angles[J]. Journal of Wind Engineering and Industrial Aerodynamics,2014,186:192—203.
[18] TANG H J,LI Y L,WANG Y F,et al. Aerodynamic optimization for flutter performance of steel truss stiffening girder at large angles of attack[J]. Journal of Wind Engineering and Industrial Aerodynamics,2017,168:260—270.
[19] 王骑,李郁林,李志国,等. 不同风攻角下薄平板的颤振导数[J]. 工程力学,2018,35(10):10—16.
WANG Q,LI Y L,LI Z G,et al. Flutter derivatives of a thin plate model under different attack angles[J]. Engineering Mechanics,2018,35(10):10—16. (In Chinese)
[20] 杨阳,张亮亮,吴波,等. 大攻角及桥面粗糙度对扁平钢箱梁涡振性能的影响[J]. 土木建筑与环境工程,2015,37(6):32—38.
YANG Y,ZHANG L L,WU B,et al. Effects of large attack angle and deck roughness on flat steel box girder vortex-induced vibration[J]. Journal of Civil,Architectural & Environmental Engineering,2015,37(6):32—38. (In Chinese)
[21] 刘小兵,张海东,刘庆宽. 大攻角下分离双钢箱梁间距对涡振特性的影响[J]. 振动与冲击,2017,36(14):202—207.
LIU X B,ZHANG H D,LIU Q K. Influence of the spacing on vortex-induced vibration characteristics of twin separate steel box girders under a large wind attacking angle[J]. Journal of Vibration and Shock,2017,36(14):202—207. (In Chinese)
[22] 陳艾荣,艾辉林. 计算桥梁空气动力学:大涡模拟[M]. 北京:人民交通出版社,2010:162—173.
CHEN A R,AI H L. Computational bridge aerodynamics:large eddy simulation[M]. Beijing:China Communications Press,2010:162—173. (In Chinese)
[23] 詹昊,廖海黎. 桥梁主梁端部翼板颤振主动控制流固耦合计算[J]. 振动工程学报,2018,31(2):276—282.
ZHAN H,LIAO H L. Flutter active control studies of bridge with flaps attached to deck edge by FSI calculation[J]. Journal of Vibration Engineering,2018,31(2):276—282. (In Chinese)
[24] 龚慧星,刘志文. 矩形断面柱体涡激振动数值模拟与机理分析[J]. 公路交通科技,2016,33(8):76—85.
GONG H X,LIU Z W. Numerical simulation and mechanism analysis of vortex-induced vibration of rectangular cylinder[J]. Journal of Highway and Transportation Research and Development,2016,33(8):76—85. (In Chinese)
[25] 祝志文,陈政清. 数值模拟桥梁断面气动导数和颤振临界风速[J]. 中国公路学报,2004,17(3):41—50.
ZHU Z W,CHEN Z Q. Numerical simulations for aerodynamic derivatives and critical flutter of bridge deck[J]. China Journal of Highway and Transport,2004,17(3):41—50. (In Chinese)
[26] WALTHER J H. Discrete vortex method for two-dimensional flow past bodies of arbitrary shape under-going prescribed rotary and translational motion[D]. Lyngby:Technical University of Denmark,1994:131—166.
[27] POULSEN N K,DAMSGAARD A,REINHOLD T A.Determination of flutter derivatives for the Great Belt Bridge[J]. Journal of Wind Engineering and Industrial Aerodynamics,1992,41(1/2/3):153—164.

