群稀疏高斯洛伦兹混合先验超分辨率重建

马子杰，赵玺竣，任国强，雷 涛，杨 虎，刘 盾

群稀疏高斯洛伦兹混合先验超分辨率重建

马子杰1,2，赵玺竣1,2，任国强1*，雷 涛1，杨 虎1，刘 盾1

1中国科学院光电技术研究所，四川 成都 610209；2中国科学院大学，北京 100049

为了得到置信度更高的超分辨率先验模型，实现重建结果在噪声和细节之间的平衡，建立了基于混合稀疏表达框架下的高斯¾洛伦兹混合先验模型。研究了该先验模型在超分算法中的应用优势和具体的应用方案。首先，根据先验信息的类型介绍了一些超分辨率算法的优势和问题。接着，提出对图像不同分量的统计特点进行单独建模的应用方法。然后，在分析了混合稀疏框架、高斯吉布斯先验和洛伦兹先验的基础上，说明了基于群稀疏框架下的高斯¾洛伦兹混合先验的超分辨率算法。最后，介绍了具体实现环节和最终迭代方案。实验结果表明，本文基本完成了在重建过程中保持细节的同时抑制噪声的改进目标，可以用于更多复杂环境的超分辨率重建要求。

超分辨率算法；先验模型；高斯¾洛伦兹；混合稀疏表达

1 引 言

成像系统受到物理极限、硬件条件以及成像环境等因素的影响具有截止频率。截止频率降低了成像系统采集图像的空间分辨率。超分辨率重建技术就是一种从低分辨率图像(或图像序列)中获得高分辨率图像的方法，被称为“第二代图像复原技术”[1]。该技术通过向图像添加高频信息，从而得到空间分辨率更高的图像。

由于超分辨率问题是一个典型的病态不适定反问题，所以为了得到真实的重建结果，给图像添加额外信息是重建的关键。不同的超分辨率算法本质上的区别是获取图像额外信息的方法不同。最主要的图像额外信息的方法有两个方面，第一是提取多帧图像序列的帧间非冗余信息，要求图像间具有亚像素位移；第二是根据一些已有的经验或者图像本身的固有属性对图像建模，这一部分被称为先验信息。这两类信息在优化目标函数中，分别称为数据一致项和先验项，在优化中分别承担对细节和总体的修正作用。图像数据优化时由于维度大，还受到噪声的影响，所以如果单纯依靠数据一致项重建，容易在优化中过拟合或产生虚假信息，甚至出现伪影，所以为图像引入合理可靠的先验信息至关重要。

图像先验信息之所为称为“先”，意味着是在重建前就提前知道的信息。超分辨率算法有很多常见的提取先验的方法。基于空间域的算法可以提取图像的结构信息、梯度信息，它们通过图像内部的梯度关系或像素间的上下文约束进行建模，这种方法在信噪比高的情况下常会取得较好的效果。基于学习的算法[2-3]。则是通过训练，在数据集中学习到“经验”，比较适用于识别和鉴别，在复原中易引入虚假信息。基于变换域的算法是在稀疏域内为先验图像建模[4]。稀疏表达常作为自然信号的约束器，不具备稀疏表达特性的信号被视为噪声或者变形等，这种方法在信噪比较低时可以达到抑制噪声的效果，但对边缘会造成一定程度的模糊。

目前常用的算法有全变分法(total variation，TV)[5-6]和基于L1范数法[7]二者，都是属于空间域的算法。TV的先验和L1范数先验对边缘的保持效果比较好，但不能捕捉自然图像的统计信息，生成的图像通常是分段线性的，可能会产生一些伪影。最大后验概率法(maximum posterior probability，MAP)算法引入了统计先验信息，减少了不连续测量的影响，且在噪声比较严重的情况下，MAP算法可以在重建的同时有效地减少噪声，其中常用的先验模型有高斯模型、马尔可夫随机场模型、吉布斯模型等。基于这些模型的重建会在一定程度上削弱边缘，使重建结果过于平滑。Schultz提出的Huber-MRF模型[8-9]的重建结果边缘锐化效果好，但对参数选取要求高，且重建结果对观测值的波动表现得不够稳定。

基于稀疏的算法[10-11]近年也有很多应用。因为自然图像的成分组成复杂，所以在基于稀疏的算法中，单一的变换域并不一定能对一幅图像进行精准的表达。例如，小波变换适合于表示图像中的平滑内容；曲波变换可以很好地表示任意方向的全局线结构；离散余弦变换在表示图像中的平滑或周期性成分方面表现出色。所以Li[12]等人提出了混合稀疏表示法(mixed sparse representation，MSR)也叫做群体稀疏表示法(group sparse representation，GSR)。它可以将不同类型的图像分量分别投射到合适的稀疏域中去。基于这种框架可以更加准确地在稀疏域内表达图像。MSR是一种很具有应用性的方法，目前已经成功应用于图像分类与图像重建中，但缺陷是各分量域之间没有完全正交，难以避免对清晰度的影响。

影响图像边缘清晰度主要由边缘信息决定，而噪声主要由平滑区域决定。分别建模优化可以对三种分量分开把控，减少对图像细节的削弱，在抑制噪声影响的同时具有保持细节的能力。为了得到一种可以兼顾信噪比和边缘清晰度的算法，本文利用MSR可以分离图像的点、线、面三种分量的特点，针对这三种分量的特点分别进行建模，得到更准确的图像先验模型。点分量以及平滑的面分量主要对图像的信噪比产生影响，根据图像的上下文约束，采用吉布斯-马尔可夫先验模型。根据人眼视觉感知的判读特性，对于图像清晰度起决定性影响的是线分量也就是边缘分量，采用洛伦兹模型对图像的边缘分量进行建模。选用洛伦兹函数为边缘分量进行先验建模的理由是：图像边缘分布直方图相较于高斯函数而言更接近洛伦兹函数[13]。所以洛伦兹模型更有利于重建出真实的边缘分量。而且洛伦兹函数是一个严格凸函数，可以使目标函数在优化中完成收敛，完全可以作为优化目标函数的模型。为了避免变换域之间不完全正交带来的优化问题，本文还融入了凸集投影迭代法(projections onto convex sets，POCS)的像素残差阈值作为收敛保证，确保迭代在交替优化中具有稳定的解。

2 理论推导

2.1 退化模型

由于成像系统具有截止频率，所以只能获得退化后的图像。假设实际场景(理想图像)为，在光学系统的焦平面上成像后经过探测器由光信号转为电信号，再经过放大器，滤波器，A/D采样器等信号处理电路，由连续的空域模拟信号转为离散的数字图像。其中可能为图像带来退化的环节有：

1) 光学系统内部的退化，包括衍射极限、光学部件的误差等原因产生的光学模糊，假设其降质矩阵为；

2) 探测器(CCD)理论和工艺上的限制使采样频率一般低于信号截止频率，不满足香农定理的完全重构条件，带来严重的混叠，假设其降质矩阵为；

3) 成像过程中还常伴随有光电子噪声(CCD尺寸限制的主要原因)、电子噪声等噪声的影响，一般成像系统的噪声可以假设为高斯白噪声，以下均用表示；

4) 相机的抖动，相机与对象之间的相对运动等。假设成像环境中的主要退化因素是相对运动，其降质矩阵设为。

综上所述，一般的成像退化过程可以表示为

其中：为退化后的图像序列，是帧数，表示感光元器件的下采样矩阵，表示光学模糊矩阵，表示运动模糊矩阵，为理想图像，为噪声矩阵。综合整个成像过程的退化，可以以来表示整个成像系统的点扩散函数(point spread function，PSF)。

2.2 配准算法

图像序列之间的运动估计和配准对多帧超分算法的重建效果有至关重要的影响。超分辨率算法的基本要求是图像序列具有非冗余信息，所以图像配准算法需要达到亚像素精度。本文采用的图像配准算法为Lucas-Kanade结合金字塔的光流估计法[14]。该方法的核心思想是利用成像系统和被测目标之间的相对运动所产生的瞬时速度场(也可以称为光流(optical flow))来确定像素点的运动矢量。为了提高计算速度，引入金字塔模型，遵照先粗后细的原则，逐层增加配准的精度，减少冗余计算。

2.3 先验模型

2.3.1 高斯-吉布斯先验

采用统计学方法进行图像超分辨率复原重建的求解过程就是对优化问题进行建模，然后采用合适的优化工具求解目标函数。在图像的平滑分量中，我们采用的建模依据是上下文约束关系(contextual constraints)，即图像中相邻像素具有依赖关系(强相关性)。根据上下文约束法则，可以对像素之间的基本位置关系进行建模。相邻像素之间是无向链接，且条件独立，具有马尔可夫性(Markov random field，MRF)。

首先，假设图像是一个非平稳随机场，则可以利用贝叶斯公式和全概率公式组建最大后验概率(MAP)公式，将最优化结构风险估计转化为图像重建的目标函数的基本框架：

其中：为退化后的图像，为理想的成像结果。

确定了目标函数的框架后，就可以选定用于求解的优化工具。由于图像特征具有马尔可夫性，即像素的灰度值只和领域有关与领域外像素无关。我们选用MRF模型作为面分量的先验模型。根据Hammersley-Clifford的等价定理，可以将较难求解的MRF条件概率问题转换为较容易求解的Gibbs问题。Gibbs分布中的核心¾能量函数的选取不同可以产生不同的先验模型。不同的Gibbs-Markov先验模型体现在不同的能量函数构建上。目前一般用的是Gauss-Gibbs先验模型，目标函数可以写为

2.3.2 洛伦兹先验

洛伦兹(Lorent)密度函数为

其中：为分布函数的中心点，为波形半值全宽，描述了函数的形状。如图1所示。

对大多数图像而言，其边缘图像直方图不再服从于高斯分布，而是更近似于洛伦兹分布，其像素点分布可以表示为

则边缘图像的概率密度函数为

为了保证目标函数在优化时的收敛和算法的稳定，先验模型的概率密度函数应该为连续的严格凸函数。洛伦兹函数是严格凸且所有点都连续的可导函数，因此可以满足重建算法稳定特性。

采用洛伦兹模型作为先验模型时，目标函数为

本文采用梯度下降法进行代价函数的迭代求解。从数学角度看，梯度的方向是函数增长速度最快的方向，那么梯度的反方向就是函数减少最快的方向。梯度下降法就是沿着函数最陡峭的方向下降，直到达到最小值，因此要求代价函数是一个严格的凸函数，否则会得到局部最小值。

得到的优化迭代公式为

2.4 基于混合稀疏框架的高斯洛伦兹混合先演算法

群体稀疏表达也叫做混合稀疏表达(mixed sparse representations)。假设图像由三个子图像组成：

1) 图像空域中的点分量s；

2) 小波(Wavelet)域内的平滑分量w；

3) 曲波(Curvelet)域内的边缘分量c。

采用非下采样轮廓波变换(nonsubsampled contourlet transform，NSCT)对图像边缘分量进行提取。NSCT是曲波变换的数字实现形式，是针对于小波变换在二维信号表达时的缺点而被提出的，它的特点就是在对频率分解时具有方向性和各向异性。因此，一幅图像在稀疏域内映射的结果也就是分量分解结果，如图2所示。

因此，我们有了图像分离的表达框架：

在此框架下对分量进行先验建模：

其次，采用高斯¾吉布斯模型对点图像和面图像进行建模，边缘图像采用洛伦兹模型。在MSR框架下的Gauss-Gibbs混合先验算法的代价函数为

图2 图像分量分解图。(a) 面分量；(b) 边缘图像；(c) NSCT横向二阶边缘；(d) NSCT纵向二阶边缘

再次采用梯度下降法求解式(11)，从最小点的初始估计开始，按照代价函数的负梯度的方向开始迭代，求取代价函数的最小值，在次迭代后，估计的高分辨率图像为

最终迭代公式为

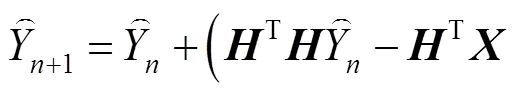
其中：是小波算子，是NSCT取边缘算子。

经过图像分量分离和分别建模以后，在不同的域内的优化是相互关联又独立进行的，不同域并不完全正交，在优化中结合了凸集投影迭代法的阈值收敛，按照像素置信度的标准作为终止标准。

算法重建从图像高分初始值(参考帧上采样)开始，在迭代中加入后验信息进行修正，直到达到预先设定的终止条件，得到重建结果。

具体步骤如下：

1) 任选一帧低分辨率图像作为参考帧；

2) 采用Lucas-Kanade结合金字塔的光流估计对低分辨率图像进行配准和校正，配准参数如表1所示；

3) 通过对低分辨率图像进行三次样条插值得到高分辨率图像初始值；

4) 按照式(14)对低分辨率图像进行超分辨率重建估计；

5) 若满足式(15)则停止迭代，若不满足则进入下一次迭代。

3 实验结果

为了检验本算法能在维持边缘清晰度的情况下，去除边缘伪影，降低噪声水平，做了几组对比实验。首先，从一幅高分辨率图像中获得一系列低分辨率图像序列，令高分辨率图像与尺寸[4´4]、标准差为1的高斯模糊函数做卷积。其次将得到的图像进行八个方向的位移，得到八幅运动矢量分别为[1,1]、[1,0]、[1,-1]、[0,1]、[0,-1]、[-1,1]、[-1,0]、[-1,1]的图像序列。然后对得到的每一帧图像在水平、垂直方向做因子为2的降采样，得到退化图像序列。最后对退化图像序列添加均值为0的高斯白噪声，方差分别为0.001、0.003、0.008、0.01、0.01。

根据式(11)中的分析，输入图像噪声较小时，模型系数较低，输入图像噪声较大时，为了更好地抑制噪声，模型系数选取稍大，因此前两组先验模型系数为0.5，0.5，第三组为0.8，0.8，后两组噪声水平较高系数取值为1，1。将得到的重建结果和目前主流算法中对边缘具有保持效果的全变分(TV)算法[15]和基于L1范数算法[16]，以及对噪声具有抑制效果的基于高斯吉布斯的最大后验概率法(MAP)[17]的结果进行对比。图3～图7展示了图像序列在不同超分辨率算法处理后的重建结果。为了更清晰地展示出边缘重建细节，每幅图像还展示了图中某个区域的放大版本。

从结果对比中可以看出：由于MAP算法对图像边缘保持效果不佳，图像的边缘出现锯齿，主观视觉效果变模糊，图像质量较差；基于L1范数和TV算法对边缘保持效果好，可以得到比较清晰的图像，但放大边缘时发现出现伪影，这是由于分段线性微分带来的虚假信息，呈现出不规律的马赛克形态，图像平滑区域内还能观察到一些椒盐噪声。本文提出的算法能保持边缘清晰度，得到工整平滑的边缘，没有伪影和噪点，图像整体噪声水平低，视觉效果最好。

4 数据分析

为了客观地评价本文提出的算法，采取了一些常用图像质量评价标准，包括SSIM(structural similarity，衡量结果与原始图像的相似度)，MAE(mean absolute error，结果与原始图像的误差绝对值的平均值)，PSNR(peak signal to noise ratio，峰值信噪比)。这几种评价方法从图像结构相似度，重构残差水平，以及噪声水平方面对重建结果进行细节和噪声的评价。表2，3，4展示了客观评价的结果。为了展示出算法在不同输入噪声的情况下对图像质量保持鲁棒性，采用了四种不同的噪声水平的输入图像。基于高斯马尔可夫的MAP算法具有对噪声抑制的效果，在噪声水平高的时候尤其明显(图6，图7中可以看出)，但在图像放大结果中可以清晰地看到出现了锯齿状边缘，可见这种全局优化的算法对整体噪声抑制效果好，但对边缘保持性较差。基于TV算法和基于L1范数的算法是分段线性算法，它们的边缘对比度高但对图像噪声没有抑制效果，甚至对噪声还有一定的放大，在噪声水平不高的时候具有很好的复原效果，但当噪声污染水平较大时就会严重影响结果的信噪比和平均绝对误差。正是因为对点线面的分别建模，避免了对噪声的放大及对边缘具有更精确的控制，使本文提出的算法无论在低噪声水平还是在高噪声水平下的重建结果均具有稳定的表现。在表中还可以看到，虽然图像内容和信噪比不同，但本文提出的算法在与其他三种算法的比较下，在每一组测试中均具有最高的结构相似度，说明基于MSR框架的Gauss-Lorenz先验算法重建出与真实图像结果最相近的结果。本文提出的算法具有最低的噪声水平，且对图像本身内容和信噪比的鲁棒性很强，结果基本上没有大的波动。实验说明本文提出的算法在保持细节的同时还能抑制噪声，在边缘保持和平滑噪声方面具有优势。

表1 配准结果

图3 Zelda重建结果。(a) 输入图像；(b) 插值；(c) TV；(d) L1；(e) MAP；(f) GLMSR

图4 Man重建结果。(a) 输入图像；(b) 插值；(c) TV；(d) L1；(e) MAP；(f) GLMSR

图5 Cameraman重建结果。(a) 输入图像；(b) 插值；(c) TV；(d) L1；(e) MAP；(f) GLMSR

图6 coco重建结果。(a) 输入图像；(b) 插值；(c) TV；(d) L1；(e) MAP；(f) GLMSR

图7 house重建结果。(a) 输入图像；(b) 插值；(c) TV；(d) L1；(e) MAP；(f) GLMSR

表2 SSIM参数评价结果

表3 MAE参数评价结果

表4 PSNR评价结果

综上所述，在主观评价和客观评价中，证明了本文提出的算法结构具有对算法重建结果质量提升的效果。

5 结 论

超分辨率算法中先验模型的真实性和准确性决定了重建结果的效果。由于自然图像的成分较复杂，任何单一的表达方式都难以完全表达。本文采用了混合稀疏表示法，将图像分成了点分量、边缘分量和面分量，在这种框架下为图像建模，将各个分量投影到合适的域中去。分离分量后，分析不同分量的特性，根据各个分量的统计特点进行有针对性的先验建模。图像的点分量和面分量采用Gauss模型，图像的边缘分量采用Lorent模型。本文采用了梯度下降法作为优化算法，为了平衡各个域内的优化步数，减少分量间不完全正交的影响，引入了POCS的像素残差阈值作为迭代终止条件。做了三组图像序列实验，与一些在边缘保持和噪声抑制上具有代表特点的算法进行了比较。实验结果表明，提出的算法在主观评价上得到了很好的结果。在客观评价中，本文提出的算法在结构复原、细节复原及噪声水平上也都取得了相对较好的结果。综上所述，本文提出的算法不仅能够为退化的图像序列提供更好的边缘复原，还能有效地抑制噪声，可以改善先验模型的建模不匹配问题，也可以很好地平衡噪声和细节的关系，适用于更多环境复杂的图像重建。

[1] Zhou C P, Gong H L.[M]. Beijing: Science Press, 2016: 6.

周春平, 宫辉力. 实用卫星遥感超分辨率理论及应用[M]. 北京: 科学出版社, 2016: 6.

[2] Zhao Y Y, Shi S X. Light-field image super-resolution based on multi-scale feature fusion[J]., 2020, 47(12): 54–64.

赵圆圆, 施圣贤. 融合多尺度特征的光场图像超分辨率方法[J]. 光电工程, 2020, 47(12): 54–64.

[3] Yu S X, Hu L M, Zhang X D,. Multi-scale guided depth image super-resolution reconstruction[J]., 2020, 47(4): 42–51.

于淑侠, 胡良梅, 张旭东, 等. 彩色图像多尺度引导的深度图像超分辨率重建[J]. 光电工程, 2020, 47(4): 42–51.

[4] Zhu F Z, Liu Y, Huang X,. Remote sensing image super-resolution based on improved sparse representation[J]., 2019, 27(3): 718–725.

朱福珍, 刘越, 黄鑫, 等. 改进的稀疏表示遥感图像超分辨重建[J]. 光学精密工程, 2019, 27(3): 718–725.

[5] Fu B, Li Y, Wang X H,. Image super-resolution using TV priori guided convolutional network[J]., 2019, 125: 780–784.

[6] Xu T, Huang T Z, Deng L J,. Hyperspectral image superresolution using unidirectional total variation with tucker decomposition[J]., 2020, 13: 4381–4398.

[7] Farsiu S, Robinson M D, Elad M,. Fast and robust multiframe super resolution[J]., 2004, 13(10): 1327–1344.

[8] Dai S S, Cui J J, Zhang D Z. Infrared super-resolution reconstruction based on adaptive threshold HMRF[J]., 2017, 38(4): 577–579, 613.

代少升, 崔俊杰, 张德洲. 基于自适应阈值HMRF的红外超分辨率重建[J]. 半导体光电, 2017, 38(4): 577–579, 613.

[9] Rezayi H, Seyedin S A. Huber Markov random field for joint super resolution[C]//, Isfahan, Iran, 2017: 93–98.

[10] Shao Z F, Wang L, Wang Z Y, Deng J. Remote sensing image super-resolution using sparse representation and coupled sparse autoencoder[J]., 2019, 12(8): 2663–2674.

[11] Li J, Zhou T, Wang W X,. Enhancement method for aviation image based on improved NSCT[C]//, Fuzhou, China, 2020: 1–3.

[12] Li F, Xin L, Guo Y,. A framework of mixed sparse representations for remote sensing images[J]., 2017, 55(2): 1210–1221.

[13] Bao D X, Li X M, Li J. Lorentzian norm based super-resolution reconstruction of medical image[J]., 2020, 37(4): 205–208.

鲍东星, 李晓明, 李金. 基于洛伦兹范数的医学图像超分辨率重建研究[J]. 计算机仿真, 2020, 37(4): 205–208.

[14] Sun C. The research on automatic registration technology of satellite remote sensing images based on hybrid methods[D]. Changchun: Jilin University, 2018.

孙超. 基于混合方法的卫星遥感图像自动配准技术的研究[D]. 长春: 吉林大学, 2018.

[15] Liu L, Huang W, Wang C,. SAR image super-resolution based on TV-regularization using gradient profile prior[C]//, Guangzhou, China, 2016: 1–4.

[16] Li Z M. Super resolution reconstruction algorithm based on L1 norm of total variation regularization[J]., 2016, 52(15): 212–216.

李志明. 基于L1范数的全变分正则化超分辨重构算法[J]. 计算机工程与应用, 2016, 52(15): 212–216.

[17] Xue C H, Yu M, Yang Y H,. MRF reconstruction based on the markov network[J]., 2013, 43(S1): 406–409.

薛翠红, 于明, 杨宇皓, 等. 基于学习的马尔科夫超分辨率复原[J]. 吉林大学学报(工学版), 2013, 43(S1): 406–409.

[18] Liu X H, Tanaka M, Okutomi M. Noise level estimation using weak textured patches of a single noisy image[C]//, Orlando, FL, USA, 2013.

Gauss-Lorenz hybrid prior super resolution reconstruction with mixed sparse representation

Ma Zijie1,2, Zhao Xijun1,2, Ren Guoqiang1*, Lei Tao1, Yang Hu1, Liu Dun1

1Institute of Optics and Electronics, Chinese Academy of Sciences, Chengdu, Sichuan 610209, China;2University of Chinese Academy of Sciences, Beijing 100049, China

Gauss-Lorenz hybrid prior SR with mixed sparse representation before and after reconstruction result

Overview:The optimization function of a super-resolution algorithm consists of two parts: a data consistency term that is dependent on input images and a prior term that is derived from a prior model. The data consistency term introduces non-redundant information between images, but it also exacerbates the noise and causes overfitting. Therefore, the selection of the prior model is crucial for optimizing the performance of the image reconstruction. In order to obtain a higher confidence super-resolution prior model and balance the reconstructed results between noise and details, this paper establishes a Gauss-Lorenz hybrid prior model based on the mixed sparse representation framework. This prior model's advantages and specific application scheme are studied. Firstly, according to the type of prior information, the advantages and problems of some traditional algorithms are introduced. Next, the statistical characteristics of different components of the image are modeled separately. Then, based on the analysis the mixed sparse framework, the Gauss-Gibbs prior and the Lorenz prior, the super-resolution algorithm based on the Gauss-Lorenz hybrid prior under the group sparse framework is illustrated. Finally, the implementation and the final iteration scheme are introduced. The aim of noise suppression while maintaining details in the reconstruction process has been completed, which can be used for more complex environments with super-resolution reconstruction requirements. This paper has three main innovations. 1) We use the group sparse framework as the basic framework of the prior model. In this paper, different components of the natural images are projected into spatial, wavelet, and curved domains respectively. The image is divided into three components: point, line, and surface. We get constraints that are closer to natural images and improve the prior confidence. 2) Line component, that is, the edge component of an image, is closer to Lorenz distribution in statistical derivation than Gaussian distribution, so Lorenz model is used to model the edge component in the curved domain; Gaussian-Gibbs model is used to model the point and area components, which can suppress noise. The three components are continuously and alternately optimized in iteration to achieve a balance. 3) The pixel residuals threshold in the convex set projection iteration method is used as the iteration termination condition to solve the problem that the optimization progress and the optimization step are not uniform in different domains. We use four detection methods: structural similarity, maximum absolute error, noise level detection and peak signal-to-noise ratio to evaluate the results of the algorithm. Whether it is the evaluation method with or without reference, the algorithm proposed in this paper obtains better evaluation results than other algorithms.

Ma Z J, Zhao X J, Ren G Q,Gauss-Lorenz hybrid prior super resolution reconstruction with mixed sparse representation[J]., 2021, 48(11): 210299; DOI:10.12086/oee.2021.210299

Gauss-Lorenz hybrid prior super resolution reconstruction with mixed sparse representation

Ma Zijie1,2, Zhao Xijun1,2, Ren Guoqiang1*, Lei Tao1, Yang Hu1, Liu Dun1

1Institute of Optics and Electronics, Chinese Academy of Sciences, Chengdu, Sichuan 610209, China;2University of Chinese Academy of Sciences, Beijing 100049, China

In order to obtain a super-resolution prior model with higher confidence and balance the reconstructed results between noise and details, this paper establishes a Gauss-Lorenz hybrid prior model based on the mixed sparse representation framework. This prior model's advantages and specific application schemes are studied. Firstly, according to the type of prior information, the advantages and problems of some traditional algorithms are introduced. Next, the statistical characteristics of different components of the image are modeled separately. Then, based on the analysis of the mixed sparse framework, the Gauss-Gibbs prior and the Lorenz prior, the super-resolution algorithm based on the Gauss-Lorenz hybrid prior under the group sparse framework is illustrated. Finally, the implementation and the final iteration scheme are introduced. The aim of noise suppression while maintaining details in the reconstruction process has been completed, which can be used for in more complex environments with super-resolution resconstruction.

super-resolution algorithm; prior model; Gauss-Lorenz model; mixed sparse representation

10.12086/oee.2021.210299

TN911.73

A

National Key R&D Program of China (2016YFB0500200) and National Natural Science Foundation of China(61905254)

* E-mail: renguoqiang@ioe.ac.cn

马子杰，赵玺竣，任国强，等. 群稀疏高斯洛伦兹混合先验超分辨率重建[J]. 光电工程，2021，48(11): 210299

Ma Z J, Zhao X J, Ren G Q,Gauss-Lorenz hybrid prior super resolution reconstruction with mixed sparse representation[J]., 2021, 48(11): 210299

2021-09-15；

2021-11-26

国家重点研发计划资助项目(2016YFB0500200)；国家自然科学基金资助项目(61905254)

马子杰(1995-)，女，博士研究生，主要从事图像超分辨率复原技术方面的研究。E-mail：ma310029650@163.com

任国强(1971-)，男，博士，研究员，主要从事光电成像与图像处理等方面的研究。E-mail：renguoqiang@ioe.ac.cn