基于大数据的电动汽车充电站选址规划方法

刘红燕 李 谨 唐 振 赖 哲

（珠海供电局，广东 珠海 519000）

0 引言

常规燃油车辆的使用，会给自然环境带来较大的负面影响。反观电动汽车，由于其使用清洁能源，已经展现出发展的动力。由于以电能为驱动的车辆，在续航里程以及充电时长上的表现不佳，因此分析充电桩选址是有必要的。

1 电动汽车充电站的基本类型

1.1 分散式

该种充电桩一般代表专用与私人、零散分布的公共充电桩，通常坐落于停车场中，对于该类充电站规划，应利用大数据确定各区域的实际需要，计算需要的充电桩总数以及位置。另外，对于该类充电桩，也可以直接分成居民区内以及公共快充两种。在居民区的充电桩，是按照区域内的电动车辆保有量，确定充电桩数量。而公共的充电桩是按照整个地区居民的充电需要与距离，以及已有的充电桩情况，采取总体规划，保障设施的覆盖率。目前，还有借助对比分析的方式，统计不同型号电动车辆的日均用电需要与最高接入次数，由此确定不同类型充电站的潜在需要，基于对应地区的需要标准，规划充电桩的建设方案[1]。

1.2 专用式

该类充电桩是专门用于存在特殊充电要求的车辆，比如出租车、公交车、共享汽车及环卫车等。当前已经建设的专用式充电站，一般是公交车与出租车方面。前者的选址规划，应基于充电需要特点，设置适宜的规划方案。举例来讲，以运营商的方面思考，应构建充电桩的需求标准模型，以此计算适宜的设施数量。另外，结合城市道路交通网络建设状况、出租车充电需要特点、容量限制、配电系统分布等，进行详细选择规划。另外，结合出租车充电的共性需要，确保充电便利的同时，还不能干扰配电网的正常运行，由此构建最佳的充电站规划模型。

1.3 公共式

该充电桩具体涵盖高速公路与城市内的公共充电桩。相关的选址规划问题上，会基于电动车辆在高速公路中的驾驶距离与电池容量，选择建设位置。并且基于建站以及养护等方面的最低成本，调整选址定容。根据现有充电桩的电量设定以及空间分布情况，合理规划充电站的位置与定容标准，即电动车辆数量的最高期望值；用户等待时间与设施养护的最小成本投入。同时，还需注重交通状况在时空上的分布格局，以及充电站中电动车辆到达率，由此缩小用户等待时长、降低设施运维费用。

2 根据运营收益选址规划电动汽车充电站

充电站运营收益一般来自于充电服务费，鉴于充电站后期的持续性应用以及运营公司的利益等，在前期建设中，应当综合机器建设成本、预计线路的改造成本、预计公变的改造成本、充电桩运营、车位租赁成本，以此确定收益标准。

2.1 经济收入

用F1表示经济收入，如公式（1）所示。

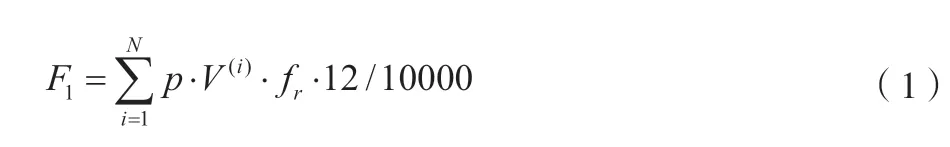
式中：p为充电站消耗一度电能得到的最终收益，p=1 元/度；V（i）为充电站在第i年时，预计所需的充电量（度/月）；fr为现实充电量和预计充电量之间的比值，fr=70%；12 为12个月；N为充电站投入应用的时间，a；10000 为F1以万元为单位进行计算。

在确定V（i）中，应当综合几项问题加以分析。首先，目标区域已有电动车辆目前需要的充电量，用v表示。该文讨论的v计算方法，是基于设施预选点，按照平台当前充电桩服务半径均值，确定预选点的覆盖半径。基于此，在服务半径中，每辆电动汽车的剩余SOC，假设该数值不足50%，说明该汽车存在充电需要，做好标记。v是指在一年中，在服务半径范围中，全部单车蓄电量之和。其次，目标区域每年的充电需求量上涨率，用ri表示。该文假设在建设后的五年间，ri维持在恒定值，也就是当地充电需求量平稳上涨，并且在五年后趋于稳定，停止增加。最后，临近充电站分布。充电桩的现实使用时，电动车辆会就近选择充电桩。对此，可借助引力模型，通过充电需要的转移矩阵，表达相邻充电桩对于用户决策的影响。该矩阵能按照充电桩现实运营期间产生的数据，持续优化，此处可利用机器学习的方式[2]。在仅有初始值时，能按照公式（2）计算。

式中：ρji为由充电站j至i过程的需要转移系数；dji为两个充电站的间距（km）。

根据公式（2）能看出，dji在不断增加的过程中，相邻充电站的充电需求转移量会相应减少。需要转移量会随之下降。

2.2 投资成本

2.2.1 建设充电桩设施的成本

按照输电模式划分，有直流与交流两种。用Pdc表示直流充电桩的建设成本，此处取值每台20000 元，数量Xdc；Pac表示交流充电桩建设成本，此处取值每台0.6 万元，数量Xac。充电桩建设总成本C1如公式（3）所示。

根据城市充电站的布置诉求，在考虑投资成本中，应综合其他几项标准。首先，Xdc须满足公式（4）。其次，在理论层面上，充电桩实际可输出电量须超过对应位置的V（5），相应的计算运算方法如公式（5）所示。再次，注重建设资金的整体投入额度，也就是要保障两种形式的充电桩数量总和，不能超过某限值。最后，假设供应电量和充电桩数量无法同时满足，须先考虑前者。

式中：R为选择快充的用户占比，假设R达到20%，对应位置须建设一个直流充电桩，反之，则不具备潜在需要。

30 为每个充电桩设备每月工作的天数；24 为设备每天工作24 h；η为充电桩设备的平均应用率，η=25%，这是充电站建设期望达到的运营状态；AV为预选位置最高充电功率；V（5）为预选位置在第五年时预计需要的电量。

2.2.2 建设充电桩设施的成本

此项投资成本，和充电站规模、选址基础设备有联系。如果预选站点当前的充电需要功率，超过对应线路的90%剩余功率，则说明此处不具备建设潜力，应当进行线路改造。而此处消耗的投资成本如公式（6）所示。

式中：C2为线路改造的总成本；L为预计线路的改造成本，取值要根据现实情况确定；α为一个变量。

α的取值范围如公式（7）所示。

式中：SL为预选站点路线，对应的剩余输送功率。

2.2.3 预计公变的改造成本

该项投资成本同样和规律、设备有联系。在预选站点对应的最高充电功率在108kW 以下，且不足其公变九成的理论剩余容量，就无须扩大公变。如果AV超过108kW，应直接加设一个公变。而假设AV处于108kW～180kW，应加设一台200kVA 公变；AV在180kW～450kW，应加设一台500kVA 公变；AV 在450kW～567kW，应加设一台630kVA 公变。

2.2.4 车位租赁成本

该项投资成本和预选站点位置有联系，按照某地的车位租赁费用标准，政府方面无须花费车位费；医院及学校，每年0.5 万元；居民区、大型商场，每年0.8 万元。由此可得到该项投资成本C4如公式（8）所示。

式中：T为不同地点场景车位租赁成本（万元/年）。

2.2.5 充电桩运营成本

该项运营成本和充电桩设备本身有关，其的计算成本如公式（9）所示。

式中：C5为充电桩运营成本；Rf为两种充电桩的运营成本，此处取值是每年0.55 万元。

2.3 收益结果

在实际求解中，可运用差分进化算法，和其他进化算法相比，其拥有以种群为核心的全局搜索方法，运用实数编码、一对一生存方法等，控制遗传操作期间的复杂程度。另外，差分进化法拥有记忆能力，能对搜索状况进行全过程跟踪，继而优化搜索方法，展现出良好的整体收敛能力与鲁班性，无须通过提炼问题特点，可在运用普通数学规划方式，应对复杂优化问题中，能有较好的表现。在差分进化算法中，利用浮点矢量，完成对种群个体的编码。算法寻优期间。在附带个体中挑选两个，得到差分矢量。下一步，挑选另外个体，其与差分矢量之间的和，确定实验个体。而后针对父代个体和对应实验个体，进行交叉作业，得到新子代个体。最后，从父代与子代个体中，进行进一步筛查挑选，把满足设定要求的个体保留下来，投入到下一代种群内。设f为适应度函数的最小值，该函数是实数向量的模式，挑选候选方案当成参数，而候选方案中输出的适应值是便是实数，以此在探索范围内的全部方案中，选出最优的一种组合。根据上文的运算过程，可得到预选站点的投资成本F2，该数值是上述的五项投资成本之和。而充电站的收益结果F，是在经济收入中扣除投资成本。充电站的相关建设方，可根据基于大数据统计得到的预选站点收益，判断对应位置的建设潜力，由此支持选址规划[3]。

3 根据充电需求预测规划电动汽车充电站

3.1 选址的影响因素

3.1.1 道路交通情况

此处假设预计假设区域的电动车辆都选择快充方法，则充电及空间特点均会道路网与配电网有影响。

一方面，交通流。把道路分成五个等级，在模拟仿真区间内，有k个时隙，而各个时隙中，t∈[k·ΔT（k+1）·ΔT]（k=0，1，2，…，K），通过确定交通流量，为电动车辆予以充电导航所需数据。在交通流的方针模型中，涉及的主要变量：交通密度—ρm（k）；速度—vm（k）；流量—qm（k）。其中，交通密度会被流量与对应车道起始状态所干扰。在（k+1）ΔT时间的交通密度等于kΔT时间和在k时隙中的交通密度相加。而对应m车道中，进入时的交通流量qm（k）=∑μ∈Imβm，φ（k）·qφ（k）；离开m车道时的交通流量则等于∑φ∈Omβm，φ（k）·qφ（k）。交通密度是受到流量影响，所以可判断其运算方式，即：（ΔT/Lm）（∑μ∈Imβm，φ（k）·qφ（k）-∑φ∈Omβm，φ（k）·qφ（k））（μ、m为车道；qφ（k）为k时隙中，道路φ交通流量；βm，φ（k）为从车道m来到φ的转弯率；Om为离开m车道的道路集合；Lm为m车道的长度）。鉴于车道形成的起始状态，m车道密度增量，能用表示。最终能推导出交通密度及交通速度。鉴于车道形成的起始状态，m车道密度增量，能用∑φ∈Omβm，φ（k）·qφ（k）表示。最终能推导出交通密度及交通速度。

上述公式中，Im表示进入m车道对应的车道集合；βμ，m表示由车道μ带来m车道的转弯率；Om表示驶离m车道对应的车道集合；Lm表示m车道的行程，即长度；（k）表示在k时隙中，车道m驶过的汽车数量；（k）表示在k时隙中，车道m中驶离的汽车数量。

另一方面，充电站的服务范畴。该项影响因素至根据待充电用户和充电站之间的行程距离，也就是常说的服务半径。对此的算法主要有两种。一是Dijkstra，基于动态规划的思路，根据两个预设点的位置，二者相互通达的若干线路中，确定最短的一条；二是Voronoi，以平面为基础，计算相关所有节点，距离对应中心点的长度，秉承最近原则，分配交通节点，由此确定服务分区。规划选址充电站时，一般是根据用户的充电决策习惯，会选择距离当前位置最近的充电桩。实际选址规划中，可运用以上两个算法，确定各预设站点的服务范畴。

3.1.2 电动车辆充电

首先，车辆状态。可用EV表示，EV=（Vdp，Clv，D，Vrp，PEV，c，Vpck，Bp）。其中，Vdp是指电动车辆驶入交通网时，对应的出发位置，各节点均是随机选择，作为汽车驾驶路线的起点；Clv是指电动车辆当下的位置，车辆按照设定路线行驶时，记录的位置资料；D是指电动车辆距离目的地的路线长度，在选中出发位置的同时，相应终点也会确定；Vrp是指当下电动车辆的剩余电量，属于动态数据，实时更新；PEV，c表示EV的功率，此处取值范围是45 kW～60 kW；Vpck表示电动汽车每行驶1 km，消耗的电能，此处取值是0.2（kW·h）/km；Bp是指在汽车充满后的电量。

其次，电动车辆的充电条件。按照电动车辆的当前状态，判断其有无充电需要。具体来说，一方面，在电动车辆剩余电量仅有30%，会进行强制充电；另一方面，电动车辆当前剩下的电量，不能支持其达到设置的地点[4]。

最后，电动车辆的充电特点。此项影响因素主要是车载电池的荷电情况，用SOC表示，如公式（9）、公式（10）所示。

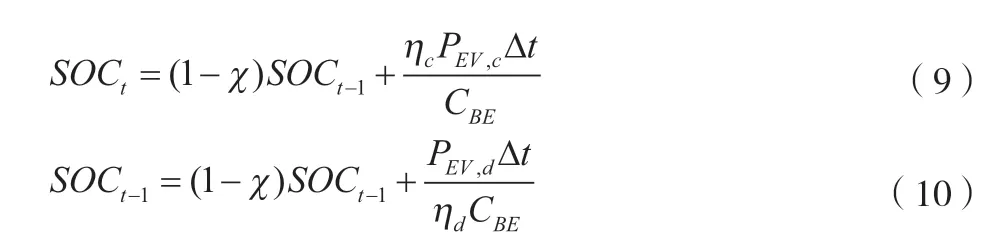
式中：SOCt与SOCt-1为各自对应电动车辆处于t与t-1 的时刻，车载电池的荷电情况；χ为自放电率；PEV，c与PEV，d为对应电动车辆在充电及放电时的功率；ηc与ηd为充电与放电的效率，ηc=0.8，ηd=1；CBE为电动车辆额定的容量。

3.2 选址规划分析

将TS作为模拟仿真的起始时间，电动车辆根据相应算法，得到初始电量值、出发地点、充电功率，而后读取其行车矩阵的终点（D），按照驾驶中的路径、速度及密度，分析不同路段的行进速度。在启动仿真模拟后，计算及记录行车时间（t1）；交通流量与车载电池的剩余电量，在车辆抵达充电站的时刻，记录行车时间（t2）与剩余电量，由此能计算出快充消耗的时长（Tc）。再得到当充电站在负荷上的时空数据，电动车辆根据到站顺序，依次充电，由此计算出在站内的排队等待时间（Tw）。在车辆充电完成后，须记录电动车辆的模拟仿真时间（t4）。在该仿真模拟中，须对多台电动车辆进行时空层面上的预测，由此确定充电需求（WE）。在实际的仿真模拟时，可将时间间隔设置成10 min，根据仿真情况，确定车辆需要的快充时间、充电负荷、排队等待时间。在车辆充个电结束后，能确定充电负荷数据，把所有充电站内的车辆充电负荷之和，规划到对应的配电网节点。在电动车辆当下剩余电量不足30%，和续航里程不足以达到设定终点，应当开始充电。

假设在充电站内的全部可用充电桩，均有车辆使用，其余汽车则须在相应序列中等待，而且还需向等待中的车辆，发送预计还需等待的时间。此时，就需要用到双层的动态排队模拟。在第一队列中的电动车辆是正在充电中的状态，第二队列则是等待中的车辆，根据到站的时间排队等待。在各个时隙下，列队处于稳定情况，对应车辆能获得预计等待时长。充电站容量符合EV需要的基础上，用户在站内等待的时长以及充电站本身的使用率，都会给用户充电满意度造成影响。

3.3 充电站的定容

一方面，新增充电桩的数量。规划建设充电站容量，应和当地电动车辆的实际充电需要相匹配。而此能通过充电桩的数目表述，如公式（11）所示。

式中：ρ为充电站用户的充电服务满意程度；Tt为充电桩平日的应用时长；Pf为充电桩本身的充电功率；Wi表示i辆车的充电需要。

另一方面，对于增加充电站数目的制约条件。根据建设充电站的潜力分析，实际选址数量应根据建设范围内，车辆充电需要与容量限制确定。如公式（12）所示。

式中：NUmin和NUmax分别为在建设范围内，预计增设充电站数目的最小值与最大值；Pehmax和Pehmin分别为在增设充电站中，预计规划的最多与最少容量；WE为电动汽车的充电需求[5]。

4 结语

在大数据的帮助下，充电站的建设方及运营方，能更容易地获取用户充电的相关记录，基于此，分析规划地区充电需要。并结合运营收益以及充电决策等，进行选址规划，并确定充电桩容量，保障各设施的应用率。