基于自适应模糊PID的导弹控制系统

王小东,周春桂,王志军,王利锋,张凯奇

(1.中北大学机电工程学院，山西 太原 030051;2.湖南云箭集团有限公司，湖南 长沙 410100)

0 引言

现代武器家族中，导弹的地位十分重要。为保证导弹稳定飞行，对目标对象进行实时跟踪，发出正确的修正偏差指令，操纵导弹改变飞行姿态，对导弹控制系统的研究极其重要。文献[1—2]指出智能控制是当前运用的最多的控制方法，非常适用于导弹这类非线性的控制系统。文献[3]提出一种PID参数优化的方法，通过优化参数提高导弹控制精度，但相比于智能控制，该方法控制效果不是很理想。文献[4]以常量定义了误差和误差变化率，验证了模糊控制理论可以应用于飞航导弹自动控制中，相比于传统PID控制，模糊控制有着更好的控制效果，但是还无法达到自适应的效果。本文针对此问题，将传统PID与模糊控制结合，提出基于自适应模糊PID的导弹控制系统。

1 导弹控制系统结构及自适应模糊PID控制算法

1.1 导弹控制系统结构

导弹控制系统是导弹上自动稳定和控制导弹绕质心运动的整套装置。它的功能是保证导弹稳定飞行，并根据制导指令控制导弹飞向目标。其控制系统主要由控制器、舵伺服机构、弹体等组成，如图1所示。导弹控制的任务就是克服导弹飞行中的各种干扰，实时准确地控制导弹姿态，使导弹自动按预定轨道飞行，因此，导弹控制精度的好坏是导弹飞行成败的关键。

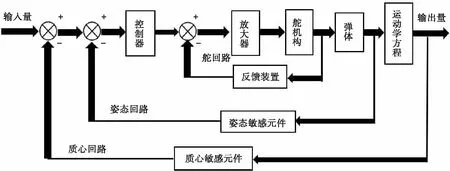
图1 导弹控制系统结构框图Fig.1 Block diagram ofMissile control system structure

控制器是整个导弹控制系统的核心部件，控制器的好坏直接影响导弹控制的精度。由于使用传统PID很难保证有较好的控制精度，然而传统PID又具有较好的鲁棒性和静态性能，因此将模糊控制与传统PID相结合可达到自适应的效果，更好地满足系统要求的性能指标。

1.2 自适应模糊PID控制算法

作为智能控制技术的重要组成部分，模糊控制已得到广泛的应用，并且控制效果明显优于传统PID控制[5-6]。模糊控制器由模糊化过程、知识库、推理决策、精确化计算四部分组成，其控制原理框图如图2所示。

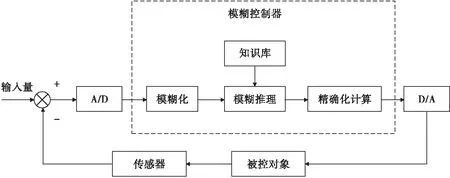
图2 模糊控制原理图Fig.2 Block diagram of fuzzy control

自适应模糊PID算法根据系统所反馈的误差信息，进行在线辨识和修正，可以实现模糊控制规则的自学习并且能在线调整控制器的参数，以便适应外界条件或环境因素的干扰，大大提高系统的控制精度和抗干扰能力，更好满足控制系统所要求的性能标准[7]。

通常以误差E及误差变化率EC作为输入，首先将输入量进行模糊化，得到相应的模糊集合。根据被控对象的控制要求设置语言变量和隶属度函数。1975年扎德(Zadeh)做出了语言变量的定义，用一个五元体来进行表征，即：[X,T(X),U,G,M]。其中X为语言变量名称，U为论域，T(X)表示语言变量值名称的集合，G为语法规则，M为语义规则，用来选取隶属度函数[8]。 模糊推理规则作为模糊控制最核心的部分，通常是一系列的IF…THEN(如果…则)模糊规则的集合，是由专家总结出来的一组模糊条件语句经验和操作技能。常见的方法有扎德(Zadeh)法，马丹尼(Mamdani)法。精确化计算是将推理出的模糊子集转换成对应的精确值，常使用的方法一般有重心法、加权平均法和最大隶属度法等。

在系统的运行过程中根据误差E以及误差变化率EC所反馈的数据与模糊关系进行在线对比，不断调节控制器参数，改善控制器的性能，使得控制效果达到更佳的状态。

2 基于自适应模糊PID的导弹控制系统

本文提出的自适应模糊PID导弹控制系统的设计关键要素包括：确定模糊论域、确定模糊子集和隶属度函数、制定控制规则、选择合适的模糊推理方法和清晰化方法，最后经过清晰化计算得到实际输出量。将模糊控制和PID控制相结合，以解决使用传统PID控制时造成导弹控制精度不高的问题。

1) 确定模糊论域。以误差E以及误差变化率EC作为输入，以比例、积分、微分的变化量(ΔKp,ΔKi,ΔKd)作为输出，输入量误差和误差变化率的论域为(-6，-4，-2，0，2，4，6)，输出量ΔKp,ΔKi,ΔKd的论域为(-3，-2，-1，0，1，2，3)。

2) 确定模糊子集和各变量隶属度函数。将输入输出变量都平均划分为7个等级：NB、NM、NS、Z0、PS、PM、PB(负大，负中，负小，零，正小，正中，正大)，隶属度函数选择对称的三角形隶属度函数。

3) 制定模糊控制规则。控制器的模糊推理采取IF…THEN模糊规则的Mamdani法推理。在制定模糊控制规则时应遵循以下原则：

当|E|较大时，应选取较大的ΔKp和较小的ΔKd;当|E|不太大时，为了使系统具有较小的超调，ΔKp应取较小些，ΔKd对系统影响较大，应取较小些；当|E|较小时，ΔKp和ΔKi应取得大些。控制规则如表1—表3所示。

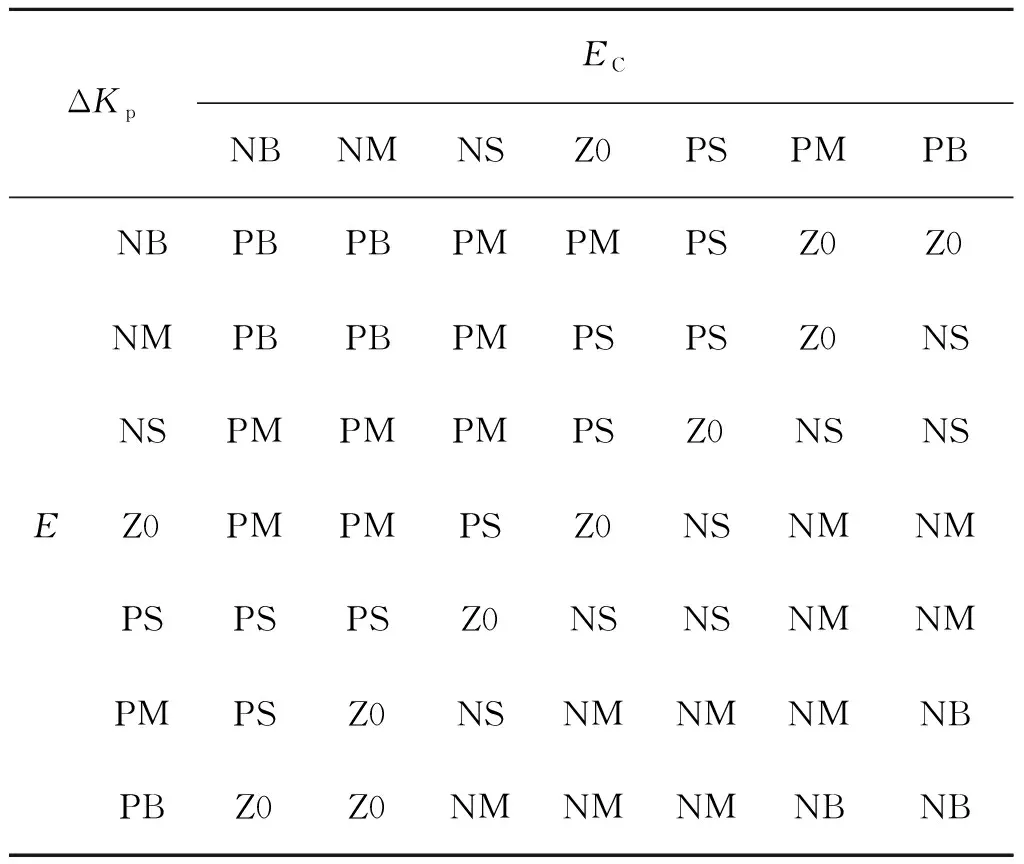
表1 ΔKp模糊控制规则Tab.1 ΔKp fuzzy control rules

表2 ΔKi模糊控制规则Tab.2 ΔKi fuzzy control rules

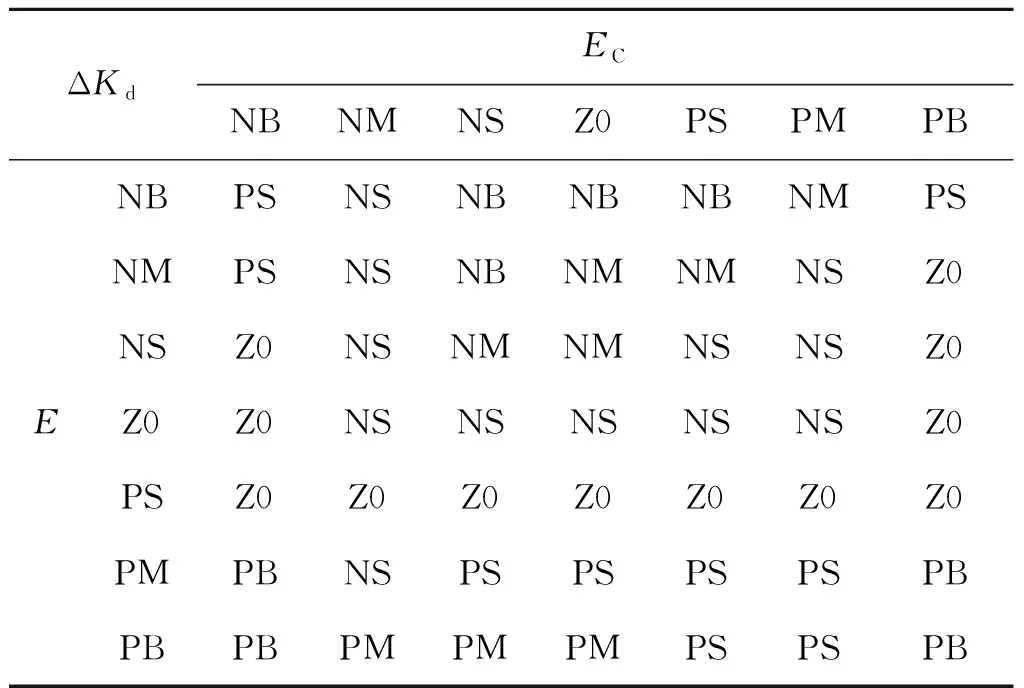
表3 ΔKd模糊控制规则Tab.3 ΔKd fuzzy control rules

4) 精确化计算。为了获得准确的控制量，就要求模糊方法能够很好地表达输出隶属度函数的计算结果。无论是最大隶属度法还是加权平均法，都是只考虑了模糊集合的一个点，而重心法能考虑到多个点的值，结果更加可靠，因此本文采用该方法进行精确化计算。

自适应模糊PID导弹控制系统是以误差E及误差变化率EC作为输入，以比例、积分、微分的变化量(ΔKp,ΔKi,ΔKd)作为输出。根据模糊规则，经过模糊推理和重心法清晰化，计算出PID控制器的三个变化量ΔKp、ΔKi、ΔKd来实现PID参数的在线调整，经过调整之后的PID 参数可以表示如下：

(1)

图3 自适应模糊PID控制结构框图Fig.3 Block diagram of adaptive fuzzy PID structure

3 系统仿真

3.1 弹体模型

根据文献[9—10]可以得到弹体传递函数如下：

(2)

式(2)中，第一个式子为俯仰通道弹体传递函数。其中KM是弹体传递系数，T1D是弹体动力时间系数，TD是弹体时间常数，ξD是弹体阻尼系数。本文将以文献[11]中某型导弹的俯仰通道为例进行数值仿真。

3.2 建立Simulink模型

1) 经典PID的Simulink模型

依据自动控制理论，在Simulink中依次放置输入信号，比例、微分、积分模块，传递函数模块，将各模块依次相连，加入示波器来观察响应曲线。在Simulink中搭建传统PID的模型如图4所示。

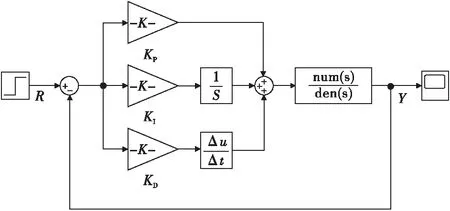
图4 PID控制系统模型Fig.4 PID control system model

2) 自适应模糊PID的Simulink模型

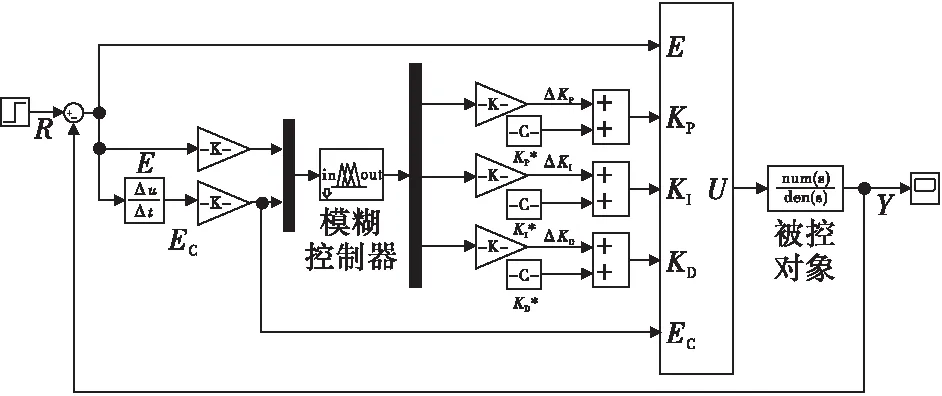
图5 自适应模糊PID控制模型Fig.5 Adaptive fuzzy PID control model control structure

3.3 仿真分析

为突出自适应模糊PID控制系统的优势，输入信号分别为单位阶跃信号和正弦信号，为验证其抗干扰性，在系统的输入端加入作用时间为0.5 s和1 s的脉冲信号作为干扰信号，比较分析了在不同输入条件下，系统在无控、经典PID控制以及自适应模糊PID三种状态的时间响应结果。

1) 正弦信号输入作用下系统的响应分析

图6为正弦激励响应曲线，可以看出，三种状态均无超调，但自适应模糊PID相比于传统PID和无控状态，上升时间更快，达到稳态时间也更快。

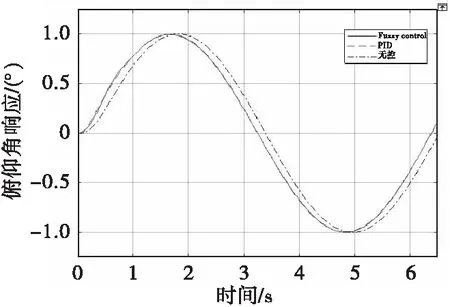
图6 三种状态下的正弦激励响应曲线Fig.6 The response curves under the excitation of sin

图7加入了作用时间为0.5 s的脉冲信号作为干扰。无控状态的超调量超过20%，上升时间是三者中最慢的；传统PID控制的上升时间缩短，但超调量明显增加，达到了40%，且震荡明显；自适应模糊PID的超调量不到20%，小于其余二者，且上升时间为三者中最快，不到0.5 s，达到稳态的时间也最短，控制效果明显强于其余二者。

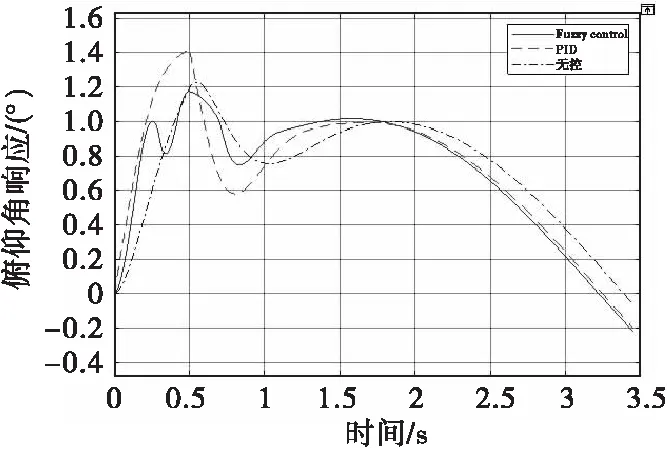
图7 加入0.5 s脉冲信号的三者响应曲线Fig.7 The response curves under the excitation of sin and 0.5 s pulse signal

图8是加入作用时间为1 s的脉冲信号得到的三者响应曲线，传统PID控制的上升时间和达到稳态的时间都比无控状态快，但超调量却增加且波动范围较大；自适应模糊PID上升时间和达到稳态时间是三者中最短，无超调，波动范围最小。

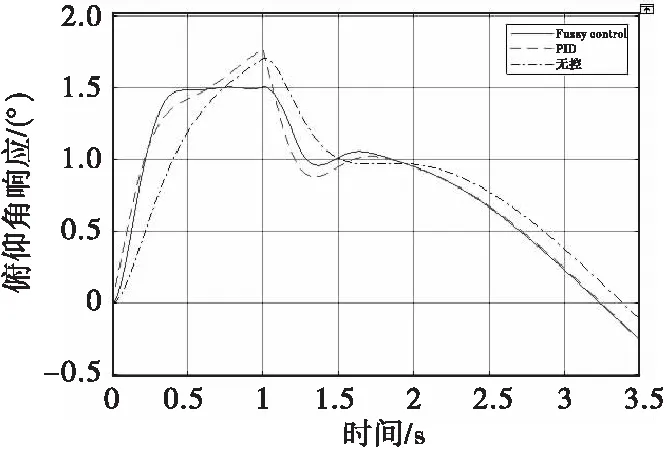
图8 加入1 s脉冲信号的三者响应曲线Fig.8 The response curves under the excitation of sin and 1 s pulse signal

2) 单位阶跃信号输入作用下系统的响应分析

图9为阶跃激励响应曲线，无控状态的超调量很小，仅有3%，但是上升时间最长；传统PID的上升时间加快但同时超调量也增加到了7%；自适应模糊PID不仅调节时间加快且没有超调量，控制效果是三者中最好的。

图9 三种状态下的阶跃激励响应曲线Fig.9 The response curves under the excitation of step

图10增加了0.5 s的脉冲信号，无控状态未达到期望值，上升时间和达到稳态时间均为三者最长；传统PID的上升时间和达到稳态的时间缩短，但超调量达到了20%；自适应模糊PID上升时间仅有0.2 s且无超调，波动范围小，达到稳态时间也最快，控制效果最理想。

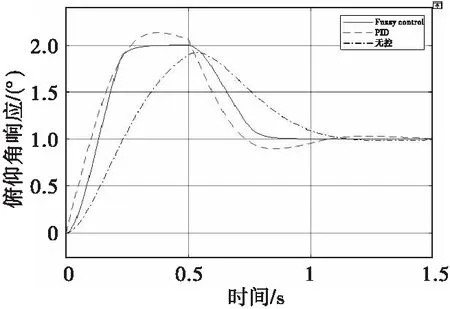
图10 加入0.5 s脉冲信号的三者响应曲线Fig.10 The response curves under the excitation of step and 0.5 s pulse signal

图11将脉冲信号的作用时间增加到1 s。无控状态超调量很小为2%，上升时间太慢，超过0.5 s；传统PID的上升时间和达到稳态时间都比无控状态短，但超调量达到了4%；自适应模糊PID的曲线上升时间快、无超调、达到稳态时间不到0.3 s，为三者最快，控制效果最好。

图11 加入1 s脉冲信号的三者响应曲线Fig.11 The response curves under the excitation of step and 1 s pulse signal

通过数值仿真结果可以看出，不论输入信号是正弦信号还是单位阶跃信号，干扰信号作用的时间无论长或短，相比较于无控状态和传统PID，自适应模糊PID的控制效果更加精准、稳定。

4 结论

本文提出基于自适应模糊PID的导弹控制系统。该系统能对PID的三个参数进行在线调整，根据被控对象的不同，计算出最优的参数供控制系统使用，从而更好地对非线性时变系统进行控制。数值仿真结果表明该控制系统具有响应时间快，上升时间短，超调量小，稳定性高的特点。在当前要求越来越高的导弹控制系统中有很高的工程应用价值。