金属护栏对洛阳地震台地电阻率干扰定量分析

侯博文 孙召华 谢佳兴 刘庆华 李志涛

（中国郑州 450000 河南省地震局）

0 引言

在地震孕育过程中，震源区应力的积累以及岩体内的膨胀破裂，均会导致该区域地下介质电性结构的改变（王志贤等，1993）。电阻率为地下介质重要的物理参数之一，合理地利用其观测资料，可以了解地下岩体应力积累、释放过程。在地震台站进行的地电阻率观测，实质上是定点电阻率观测，其测值为同一地点地下固定体积内电阻率随时间的变化。作为一种主动源观测方法，该方法来源于物探中的直流电法，但又区别于物探电法观测所强调的电阻率随空间的变化。因此，地震台站测区内场地条件的变化都会引起该区域电阻率的变化。在实际观测中，除了地表温度、湿度等气象因素及水文条件的季节性变化可引起测区地电阻率变化外，电磁干扰、金属导线类干扰和测区内大面积施工，也都会改变测区内的电性结构从而引起测区地电阻率变化，而这种干扰变化往往具有破环性。

针对金属导线类干扰，我国地电工作者开展了许多理论研究和实验分析工作。卫定军等（2009）采用等效电路分析方法，对固原地震台地电阻率的铁丝网干扰作了定性分析和解释，指出铁丝网搭建使得测量极电位差增加，进而造成固原地震台视电阻率测值增加。张秀霞等（2009）利用绝缘装置处理铁丝网，成功将铁丝网对地电阻率观测的影响进行消除，并结合测区电性结构作出定性分析与解释。张磊等（2010）对全国多数地电阻率台站进行调研分析，认为金属类管网产生的干扰与其长度、方位密切相关。汪志亮等（2002）分析了太原地震台测区附近埋设金属灌溉管道对地电阻率观测的影响，并指出平行于测道铺设的金属管线的影响最显著，斜角或垂直铺设的影响相对较小。解滔等（2013）利用三维有限元模型下计算了宝昌地震台测区内埋设钢缆对地电阻率观测的影响，指出表层土壤在稳定冻结阶段钢缆对观测的影响非常小，在完全融通阶段的影响最大，在非稳定冻结阶段的影响介于二者之间，并给出对称四级装置观测时测区介质对地电阻率观测的三维影响系数分布情况。杨龙翔等（2020）利用有限元法对周口地震台地电阻率进行数值计算，认为2015年周口地震台地电阻率年变异常主要受测区内建立金属大棚的影响。王同利等（2017）采用三维有限元模型对延庆地震台地电阻率测区内铁管、铁脚架和铁质地基对观测数据的影响进行数值模拟分析，指出铁质干扰介质的排列方向与测线方向密切相关，当干扰介质与观测测线方向一致时，干扰变化较大。张国苓等（2017）利用有限元法定量计算了挖土水坑蓄水量和砖厂建设对兴济地震台地电阻率观测的影响。

洛阳地震台定点地电阻率观测始于1972年，观测资料质量较好，年变化和趋势性变化清晰。2018年11月台站测区内238省道上陆续安装了金属导线状护栏，导致地电阻率NS、EW测道观测数据均出现了不同程度的阶跃变化，对观测产生了较大干扰。为了对该台地电阻率数据异常进行较准确的判定，本文利用洛阳地震台建台时的钻孔资料和观测资料，结合电测深曲线建立三维地电阻率观测物理模型，采用有限元数值分析方法，定量计算金属护栏对洛阳地震台地电阻率观测的影响，并讨论了测区内位于地表的金属导线在不同属性（与测道夹角、长度、电阻率、有效横截面积）情况下对观测产生的干扰随时间的变化特征，以期为其他台站判别和定量分析类似干扰提供参考。

1 台站基本情况

1.1 台站简介

洛阳地震台位于河南省洛阳市南郊，距市区约5 km，隶属洛阳市洛龙区魏湾村辖区。台站地电阻率观测场地位于洛阳市南郊洛龙区龙门山，地质构造上处于秦岭纬向构造带东段、华北板块的西南部，位于祁吕贺“山”字型构造的弧顶部位，并与新华夏构造在此交汇。测区附近有2条大断层，其一是测区东的伊河断层，沿伊河展布，走向NE，倾向NW；其二是新安—草店断层，走向NW，倾向WS，倾角为60°—70°。2个断层均为活断层，而测区位于伊河断层的破碎带边缘，即南侧（上盘）伊河的一级或二级阶地上（河南省地震局，2005）。

目前，洛阳地震台使用中国地震局预测研究所监制的ZD8BI型地电仪进行地电阻率观测，采用对称四级直流供电观测装置，因受场地条件限制，观测中选用“L”型布极方法，分别沿近NS、EW两个互相垂直的方向布设测线，其中，供电极距LAB均为1 000 m，测量极距LMN均为300 m（图1），电极埋深均为2.0 m，外线路采用电缆架空方式。台站观测装置、测量仪器、外线路和电极等均符合地电阻率台站观测的技术要求（中国地震局，2006）。

1.2 干扰情况简介

自2018年12月金属护栏安装完成后地电阻率数据出现异常变化，其中，NS测道数据阶跃变化幅度0.51 Ω·m，相对日均值变化0.86%；EW测道数据阶跃变化幅度0.23 Ω·m，相对日均值变化0.47%。数据出现变化的时间与护栏安装时间同步，并且安装护栏对地电阻率年变曲线亦有一定影响。将2015—2017年洛阳地震台地震平静期地电阻率数据进行平均并时序叠加后得到的数值作为正常预测值（图1虚线），与后期的观测值对比后发现，2018—2019年洛阳地震台NS测道地电阻率出现明显抬升变化，EW测道的出现小幅下降变化，并且2020年该异常变化持续，未恢复正常（图1实线）。

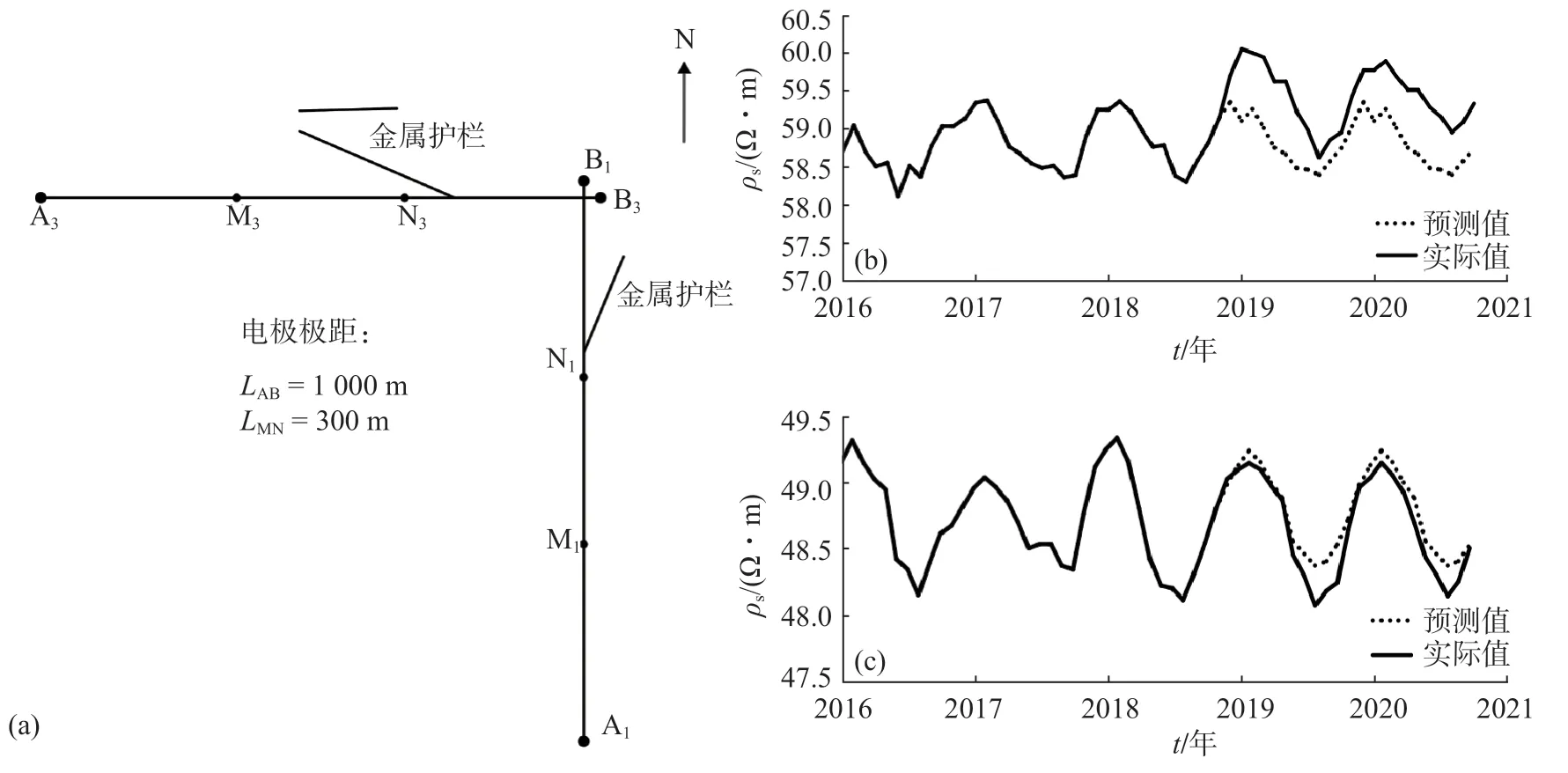
图1 洛阳地震台地电阻率观测布极方位及月均值（a）地电阻率观测布极方位；（b）NS测道地电阻率实际值与预测值；（c）EW测道地电阻率实际值与预测值Fig.1 The electrode layout of the geoelectrical resistivity observation and the monthly mean value observation curve of the Luoyang Seismic Station

根据洛阳地震台建台时岩性资料和电测深曲线（图2），洛阳地震台测区地下介质覆盖层为第四纪松散沉积层，其主要成分为亚粘土并含有少量粉砂，电阻率较高；第2层 主要为含水的砂卵石层，砂卵石大小不均，并且孔隙中含有少量砂土，电阻率最低；第3层以石灰岩和泥质灰岩为主，较松软，夹有泥质；第4层以石灰岩为主，质地坚硬，电阻率最高。将电测深反演结果作为地层电性结构参数，建立水平层状4层模型并假定每层介质电阻率均匀（表1）。

图2 洛阳地震台电测深曲线Fig.2 Resistivity sounding curves of Luoyang Seismic Station

表1 洛阳地震台水平层状电性结构Table 1 Horizontal layered electrical structure at Luoyang station

2 有限元数值分析

2.1 稳恒电流场有限元方法

有限元法是一种求解偏微分方程边值近似解的数值分析方法，其优点是通过采用小单元最大程度地逼近几何模型。地震台站定点地电阻率观测时采用的是直流电对称四级观测装置，可将该观测系统视为稳恒电流场进行计算，计算时满足麦克斯韦方程组和电荷守恒定律，电位分布满足泊松方程，公式为

式中，V为直流电源I产生的电位；σ为介质电导率；δ（x,y,z）为狄拉克δ函数。

有限介质空间的全部边界为Γ；一部分边界（地表）没有电流流出，满足纽曼边界条件记为Γn；其余边界记为Γd，满足狄利克雷边界条件。因此，式（1）满足边界条件Γ=Γn+Γd，其中，Γn满足(∂V/∂n)|Γn=0；n为边界指向区域外的法线方向；Γd满足V|Γd=p。应用虚功原理可得到稳恒电流场泊松方程的有限元弱解形式（解滔等，2015）

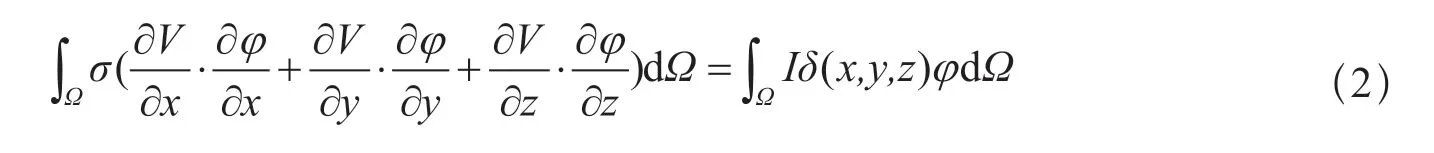
式中，Ω为计算区域；φ为任意的虚位移函数，在满足狄利克雷条件的边界上，虚位移函数φ=0。通过对模型单元离散化，施加电流源和边界条件，再对每个单元的点位进行有限元数值计算，得出测量电极之间的电位差，最后通过装置系数计算出电阻率值。

2.2 模型建立

利用有限元法建立三维水平层状介质模型，采用表1所示的电性结构参数，地层单元采用soild69八节点热—电六面体单元，金属护栏采用link68二节点热—电单轴线单元。导线单元电阻率设置为合金材质电阻率1.6×10-6Ω·m，有效横截面积为0.001 m2。地表模型中供电极距LAB=1 000 m，测量极距LMN=300 m，电极埋深为2 m，供电电流为2 A，与实际电阻率观测装置一致。地表边界满足纽曼边界条件，水平方向和垂直方向可视为无穷远边界，施加狄利克雷边界条件（V=0），当模型水平尺寸满足大于6倍AB、模型厚度满足大于2倍AB时，此时边界效应对计算的影响已小于仪器精度（解滔等，2014）。最终模型水平尺寸设置为6倍AB，最底层厚度设置为2倍AB，模型大小为6.0 km× 6.0 km×2.3 km。因NS、EW两测道电性结构不一致，因此，本文将采用实际解释结果分别建立模型进行计算。为了验证模型单元划分的合理性，将模型计算结果与由电阻率转换函数递推公式得到的理论解进行对比（表2），由表2可见，二者具有较好的一致性。

表2 洛阳地震台视电阻率计算值与理论值对比（Ω·m）Table 2 Comparison between theoretical and calculated apparent resistivities at Luoyang station

实际观测中台站地电阻率存在年变现象，该现象主要受地表浅层介质电阻率的影响而表现出同步变化。通常，夏季气温上升，降雨量增加，浅层介质电阻率下降；冬季气温下降，降雨量减少，浅层介质电阻率上升。而中深部介质受气温和含水率季节性变化的影响较小，因而电阻率相对稳定。

温度对浅层介质电阻率的影响可分为2个方面，一是温度对地层中土壤骨架及孔隙水电阻率的影响；二是当温度低于0℃时，土壤中水凝结成冰晶之后对浅层介质电阻率的影响。根据大气温度与地表温度间的经验关系，本文以气温为基础，设地气温差为2.0℃，计算地温数据。由于地表浅层较薄，因此，地温梯度忽略不计。当地温在0℃以上时，浅层介质电阻率随着温度的下降而上升；当地温在0℃附近时，水溶液会逐渐凝结成冰，因此，在结冰前后浅层介质电阻率将会突变；当地温在0℃以下时，浅层介质电阻率主要取决于溶液中未冻水的含量。基于洛阳地震台地理位置，主要考虑地温在0℃以上时浅层介质电阻率随温度的变化情况。根据前人（李成保等，1989）研究结果可知，对于一定的土壤介质来说，电导温变率为常数，不随温度而变。因此，只要精确测定2个温度下的电导率，就可求得电导温变率，并换算成不同温度（0℃以上）下的电阻率。经过对模型的多次调试，最终发现当受温度影响的地表浅层厚度为8 m时，往年无干扰的实际观测值年变幅度与模型计算值年变幅度基本接近。

降雨对地电阻率的干扰不但包括可引起浅层电阻值的变化，同时随着雨水的渗透，浅层厚度、湿度也发生变化。当土壤湿度较小时，土壤中水分稍增加，孔隙连通性即可得以极大改善，进而孔隙溶液中离子浓度增加，电阻率下降较快。当湿度达到一定程度时，土壤电阻率趋于10 Ω·m，并基本保持稳定（孙旭等，2019）。洛阳地震台测区内地表潜水位面较浅，常年为2 m左右，因此当雨水渗透深度大于2 m时，并不会引起2 m以下地层电性结构的变化。对受降雨影响的地表浅层厚度模型进行多次调试后发现，当受降雨影响的地表浅层厚度与潜水位面深度一致时，受降雨影响的实际观测值变化量与模型计算值变化量接近，而此时降雨对模型计算值年变幅度的影响基本没有改变。因此，本文仅将温度变化作为影响洛阳地震台地电阻率年变化的主要因素。

3 有限元法计算结果

3.1 金属护栏对洛阳地震台地电阻率短时干扰

洛阳地震台地电阻率数据自2018年12月开始出现异常，通过现场异常核实发现，238省道金属护栏已经全部安装完毕，其在NS、EW测道附近的分布如图1所示。因此，分2018年12月金属护栏安装前、后2个时间节点进行研究。

由洛阳地震台安装金属护栏前后地电阻率观测值与计算值对比（表3）可见，位于NS测道的金属护栏会导致地电阻率观测值上升，而位于EW测道的金属护栏则会导致地电阻率观测值下降。NS测道安装护栏前后模型计算值之差与实际观测值之差相差不大，但略大于实际观测结果，这可能与模型中导线单元的电阻率有关。在模型计算中，金属护栏与地面接触良好，导线单元的作用可以充分体现；而在实际观测中，金属护栏的电阻率大于模型设定值。此外，模型计算值总体比实际观测值小，这种计算结果的差异可能是地下电性结构简化程度较高造成的。

表3 洛阳地震台安装金属护栏前后地电阻率观测值与计算值对比（Ω·m）Table 3 Comparison of observed and calculated geoelectrical resistivity before and after the installation of metal barriers at Luoyang seismic station

3.2 金属护栏对洛阳地震台地电阻率年变干扰

地表低阻干扰源对地电阻率观测的影响不是固定不变的，而是随着测区介质电阻率的改变而发生变化（解滔等，2016）。模型中受温度影响的地表浅层厚度设置为8 m，浅层介质电阻率的获取方式为：采用2016年8月至2020年10月气温月均值数据，通过电导温变率换算公式（李成保等，1989）计算电阻率，将其作为浅层介质电阻率的年变化值。据此，计算洛阳地震台地电阻率在有无金属护栏干扰下的变化情况。

将洛阳地震台2015—2017年地震平静期数据进行平均并时序叠加（因此次干扰自2018年开始，所以未加入2018年实测数据进行计算），所得结果作为2019—2020年预测值。将受温度影响且无金属护栏干扰的模型计算结果作为模型计算值。在消除简化电性结构产生的误差后，将二者进行对比（图3），由图3可见，年变化趋势基本一致。说明温度变化是洛阳地震台地电阻率年变化的主要影响因素，并且可将该模型可以作为洛阳地震台的基本模型来分析数据异常变化。在添加金属护栏后，模型计算值基本接近于测区有护栏干扰的实际观测数据，总体受影响趋势与实际观测值上升或下降变化同步。根据地电阻率三维影响系数理论（解滔等，2015），低阻干扰源位于影响系数为正的区域会导致地电阻率观测值的下降变化，而位于影响系数为负的区域则会导致地电阻率观测值的上升变化，这与洛阳地震台实际观测数据相符。因此，金属护栏是造成洛阳地震台地电阻率年变趋势性改变的主要因素。

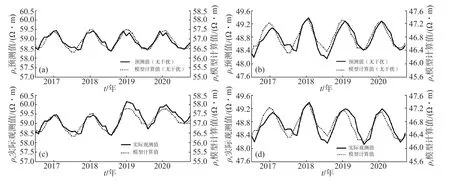
图3 洛阳地震台地电阻率观测受金属护栏干扰的有限元分析（a）NS测道地电阻率预测值与模型计算值（无干扰）；（b）EW测道地电阻率预测值与模型计算值（无干扰）；（c）NS测道地电阻率实际观测值与模型计算值（有干扰）；（d）EW测道地电阻率实际观测值与模型计算值（有干扰）Fig.3 Finite element analysis of metal barrier interference

4 干扰特征讨论

在计算过程中发现，金属护栏对观测产生干扰的幅度与测区电性结构、相对测线位置、金属护栏自身的基本属性等密切相关。将采用典型“H”型电性结构参数，建立3层水平层状均匀介质模型（图4）。供电极距LAB=1 000 m，测量极距LMN=300 m，供电电流为2 A，均与我国大多数地电阻率台站一致。下面讨论地电阻率测区内位于地表的金属导线在不同属性（与测道夹角、长度、电阻率、有效横截面积）情况下对观测产生干扰的形态和幅度随时间的变化特征。

图4 地电阻率三维模型Fig.4 3D model of geoelectrical resistivity

4.1 不同夹角的金属导线对地电阻率年变的影响

3层水平层状介质模型参数如图5（a）所示，分别计算金属导线位于电极MN与电极AM之间且与测道不同夹角的情况下地电阻率观测年变情况。设置金属导线长度为100 m，使其位于电极MN以及电极AM的中间，导线与测道间夹角如图5（b）所示，分别为0°、30°、60°、90°，导线电阻率为铁质电阻率9.78×10-8Ω·m，导线有效横截面积为0.001 m2。假设地表浅层介质电阻率季节性变化为模型第1层介质电阻率变化，变化范围如图5（c）所示。

图5 不同夹角金属导线对地电阻率观测影响模型（a）3层水平层状模型；（b）不同方位金属导线布设模型；（c）第1层介质电阻率随季节的变化Fig.5 Influence model of geoelectrical resistivity observation for metal wires with different angles

当金属导线位于电极MN之间时，模型中无干扰时的计算值与金属导线与测道之间不同夹角时的计算值如图6（a）所示。此时，受干扰曲线位于无干扰曲线的下方，即金属导线将引起地电阻率观测值的下降变化。随着金属导线与测道间夹角增大，该变化量逐渐减小。当金属导线与测道垂直时，地电阻率观测值基本不受金属导线影响。当金属导线位于电极AM之间时，模型中无干扰时的计算值与金属导线与测道之间不同夹角时的计算值如图6（b）所示。此时，受干扰曲线位于无干扰曲线的上方，即金属导线将引起地电阻率观测值的上升变化。随着金属导线与测道间夹角增大，该变化量逐渐减小。当金属导线与测道垂直时，地电阻率观测值基本不受金属导线影响。

金属导线与测道间夹角的不同对地电阻率年变形态的影响也不同。当金属导线位于电极MN之间时[图6（c）]，金属导线的存在对无干扰时的地电阻率年变形态具有放大作用，但随着夹角的增大，放大作用逐渐减小，直到导线与测道垂直时该影响消失。而当金属导线位于电极AM之间时[图6（d）]，金属导线的存在对地电阻率年变形态有抑制作用，随着夹角的增大，抑制作用逐渐减小，直到导线与测道垂直时该影响消失。

图6 金属导线夹角对地电阻率年变的影响（a）不同夹角金属导线位于MN之间季节性变化；（b）不同夹角金属导线位于AM之间季节性变化；（c）不同夹角金属导线位于MN之间年变幅度；（d）不同夹角金属导线位于AM之间年变幅度Fig.6 The influence of metal wire angles on the long-term variation of geoelectrical resistivity observation

4.2 不同长度的金属导线对地电阻率年变的影响

模型中采用相同的电性结构，金属导线分别位于电极MN与电极AM之间，与测道夹角为0°，导线有效横截面积为0.001 m2，导线电阻率为铁质电阻率9.78×10-8Ω·m，长度分别设置为50 m、100 m、150 m、200 m、250 m。根据模型第1层介质电阻率变化，地电阻率年变形态计算结果如图7所示。

由图7可见，金属导线位于电极MN之间时，导线长度的增加将引起地电阻率观测值减小，此时地电阻率年变形态与正常年变一致，并且导线长度的增加对地电阻率年变形态具有放大作用。当金属导线位于电极AM之间时，导线长度的增加将引起地电阻率观测值增大，并且对地电阻率年变形态具有抑制作用。当抑制作用持续加强时，干扰动态变化幅度大于原有的年变幅度，此时将引起年变的反向变化，随着导线长度的增加，该反向变化形态会逐渐放大。

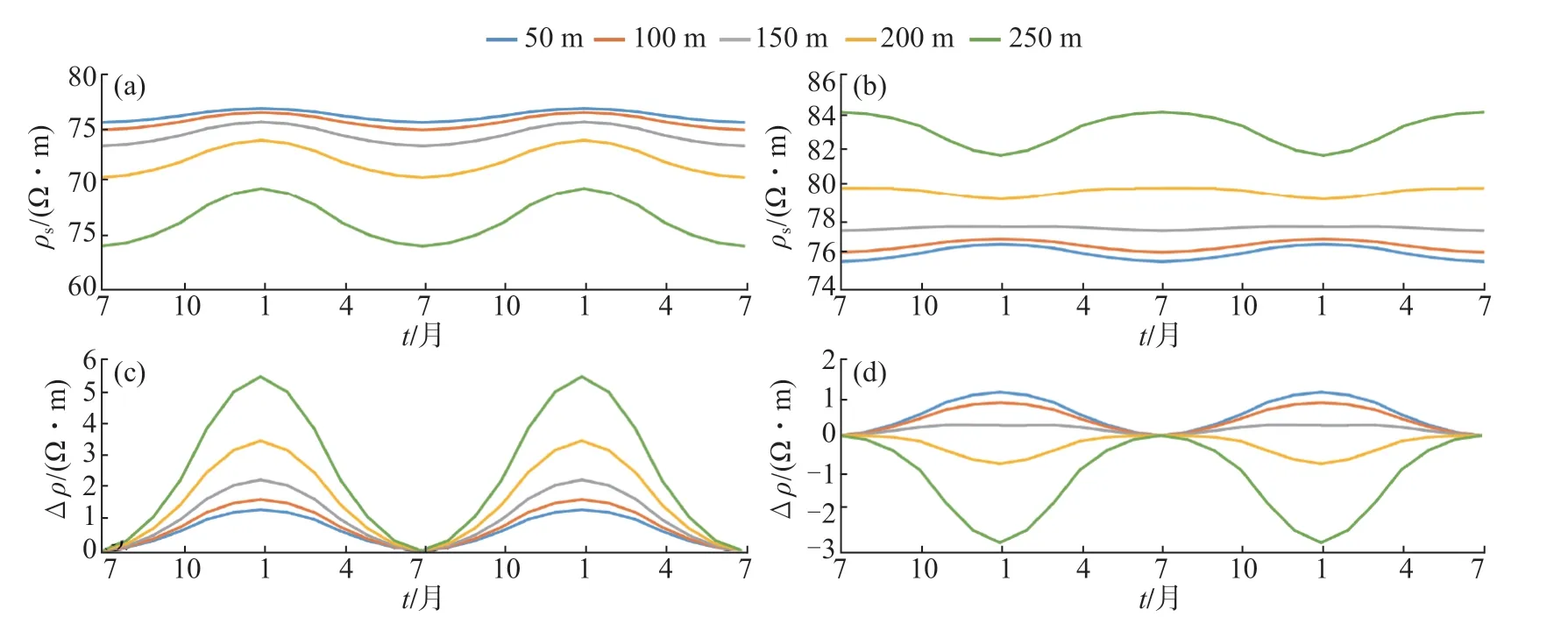
图7 金属导线长度对地电阻率年变的影响（a）不同长度金属导线位于MN之间季节性变化；（b）不同长度金属导线位于AM之间季节性变化；（c）不同长度金属导线位于MN之间年变幅度；（d）不同长度金属导线位于AM之间年变幅度Fig.7 The influence of metal wire length on the long-term variation of geoelectrical resistivity observation

4.3 不同电阻率的金属导线对地电阻率年变的影响

不同电阻率的金属导线对地电阻率观测产生的影响是不同的，导线电阻率越低，干扰幅度越大，但是否会对地电阻率年变产生类似影响呢？设置金属导线长度为100 m，将其置于电极MN与电极AM中间，与测道夹角为0°，导线有效横截面积为0.001 m2，导线电阻率分别为1.0×10-2Ω·m、1.0×10-4Ω·m、1.0×10-5Ω·m、1.0×10-7Ω·m。计算结果如图8所示。

图8 金属导线电阻率对地电阻率年变的影响（a）干扰幅度随金属导线电阻率的变化；（b）不同电阻率金属导线位于电极MN之间；（c）不同电阻率金属导线位于电极AM之间Fig.8 The influence of metal wire resistivity on the long-term variation of geoelectrical resistivity observation

由图8可见，当导线电阻率＞1.0×10-3Ω·m时，该导线对地电阻率观测数据几乎没有影响。随着电阻率降低，干扰幅度快速增加，并且对地电阻率年变形态的放大或抑制作用增强。当导线电阻率＜1.0×10-7Ω·m时，干扰幅度趋于稳定并达到最大值，此时导线对地电阻率年变形态影响最大。

4.4 不同横截面积的金属导线对地电阻率年变的影响

金属导线对地电阻率年变的干扰幅度与导线有效横截面积间的关系如图9（a）所示。由图9（a）可见，横截面积越大，干扰幅度越大。当横截面积＞1.0×10-3m2时，干扰幅度达到最大值，并趋于稳定。同样以图5所示模型为例，其他参数固定不变，导线有效横截面积分别设置为1.0×10-3m2、1.0×10-5m2、1.0×10-6m2、1.0×10-8m2，计算导线位于电极MN与电极AM之间时对地电阻率年变的影响，计算结果如图9（b）、9（c）所示。由 图9（b）、9（c）可见，无论导线位于电极MN还是电极AM之间，导线横截面积的增加均会使地电阻率正常年变形态有较大的改变。横截面积在一定的范围内，该作用会快速加强直至达到最大值，此时对地电阻率年变形态影响最大。

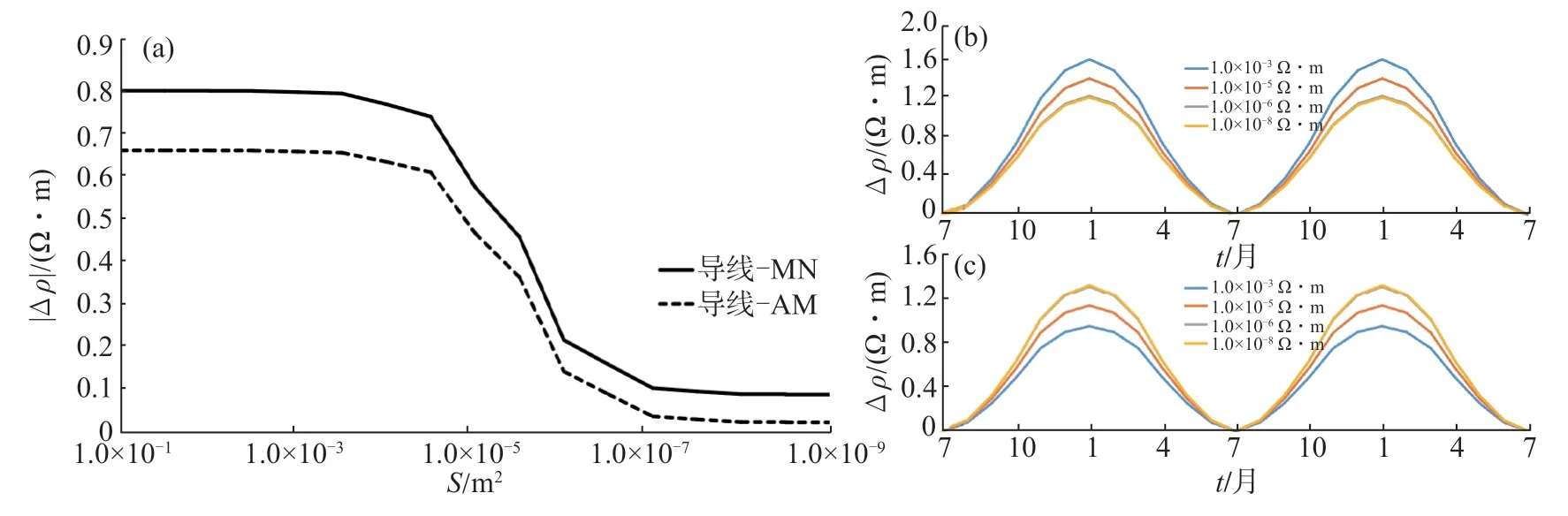
图9 不同横截面积金属导线对地电阻率年变的影响（a）干扰幅度随金属导线横截面积的变化；（b）不同横截面积金属导线位于电极MN之间年变曲线；（c）不同横截面积金属导线位于电极AM之间年变曲线Fig.9 The influence of metal wire cross-sectional areas on the long-term variation of geoelectrical resistivity observation

5 结论

采用三维有限元数值计算方法定量分析了洛阳地震台测区内金属护栏对地电阻率观测数据的影响，并计算了地表金属导线在不同属性情况下对观测产生的影响，得到以下认识。

（1）洛阳地震台测区内金属护栏会引起NS测道地电阻率观测值的上升变化，引起EW测道地电阻率观测值的下降变化，对年变影响趋势与实际观测数据同步。低阻体干扰源所在位置不同，对实际观测产生影响的变化方向和幅度也不同，这与前人结果吻合。在计算过程中还发现，温度是影响洛阳地震台地电阻率观测数据年变的主要因素，这可为今后该台地电阻率异常分析提供一定参考。

（2）在有限元数值计算中，初始的电性结构模型非常关键。洛阳地震台地电阻率模型计算值比实际观测值小，原因可能是数值计算模型与测区内实际地下电性结构之间存在一定差异，说明应用水平层状模型替代实际地下电性结构有一定的局限性，但从趋势上对观测数据异常进行快速判定时，该模型仍有一定的参考意义。

（3）不同参数的金属导线对地电阻率年变形态的影响是不同的。导线与测道夹角减小、导线长度增加、导线电阻率减小及导线横截面积增加等，均使导线对地电阻率年变形态的影响作用增强。其中，导线长度的变化对地电阻率年变影响最大，在影响系数为负的区域，导线长度增加甚至会引起地电阻率年变形态的反向变化。

（4）测区内低阻体干扰源对地电阻率观测的影响往往是具有破环性的，破坏程度取决于低阻体的自身性质，所以在日常观测中，应尽量保护好地电阻率场地观测环境，避免干扰源给数据带来的影响，以免干扰数据与地震信息耦合在一起，影响利用地电阻率数据的地震前兆分析。